基于标记位的低密度格码整形方案*

朱联祥，付孟孟

(重庆邮电大学信号与信息处理重庆市重点实验室，重庆 400065)

1 引言

低密度格玛(Low Density Lattice Codes，LDLC)是2007年结合低密度奇偶校验码(LDPC)和格码提出的信道编码技术，其编码采用雅克比迭代，译码采用高斯迭代，编译码复杂度较低。有研究证明，在误码率为10－5的条件下，当码长 n=10 000时，LDLC码距离信道容量仅有0.8 dB［1］。这些良好的性能都使得LDLC码在未来通信系统中的应用成为可能。

由于LDLC码的研究还处于初级阶段，目前对LDLC码的研究主要包括编译码算法和H矩阵的构造，而这些研究都是在功率不受限的高斯白噪声(Additive White Gaussian Noise，AWGN)信道下进行的。LDLC码经过编码后，码字的平均功率增加，同时峰值功率也增大，导致信号的动态范围变大，不能在功率受限的信道中传输，所以必须在编码前对它进行整形处理，以控制编码后功率的增加［2－4］。整形的目的就是在编码前对信息序列b'进行处理，使得输入的信息序列只映射到整形区域的格点上，最终使编码后信息的平均功率不大于未编码时的信息平均功率，最终达到控制功率的目的。把输入信息矢量b映射为矢量b'的过程叫做整形。在相同传输条件下，整形前后平均功率的减少称为整形增益。整形增益和编码增益是两个不同的概念，它们是相互独立的［5］。

理想的整形方法是定义整形区域为一个超球形，将信息序列b映射到这个超球体内，使得每个码字都服从高斯分布，这样的整形理论上可以达到1.53 dB的整形增益［6］。但是将信息序列映射到一个无限维的超球体内非常复杂，实际操作中难以实现。目前对于整形的研究还比较少，针对LDLC码还没有切实可行的整形方案。

文献［7］中Sommer提出了3种整形思想，分别是超立方体整形、系统整形、嵌套格整形。这3种整形方法是把编码前的信息序列bi看作是星座图上的点，根据格码整形的思想对bi进行处理，以达到整形的目的。但是文献中提到的这3种整形方法都是基于特定的下三角校验矩阵进行的，具有特殊性和局限性。同时，在系统整形中，作者提出一种系统编码，即要求编码后的码字中包含编码前的信息序列，目前的LDLC研究中并没有这样的码字存在，所以该算法对目前LDLC码的整形并不适用。

针对LDLC码目前的研究现状，本文提出了一种基于标记位的LDLC码整形方案:将输入的信息序列映射到星座图中，把这些信息序列分为标记位和非标记位，根据LDPC码的校验矩阵H和Tanner图，对标记位信息进行整形处理，并利用最小和算法求出整形后的序列，使得整形后信息序列的平均功率达到最小。该算法使用于目前LDLC码研究中用到的所有校验矩阵，具有普遍性，而且该算法复杂度低，容易实现。

2 相关理论

下面通过图1的一个编码调制系统对符号位整形方法进行简单的介绍。假设有一个16×16的方星座图，其中d2min=1。图1中的星座映射是将每4个状态的信息zabc映射到zabc.1上，其中，把z看作是标记位，abc看作是非标记信息位。就是把信息序列b分成两部分，即z和s，其中z作为标记位，s作为非标记位。标记位整形就是通过整形改变标记位Z，但是非标记位的信息不变，通过选择标记位的编码序列，使得整个信息序列映射到星座图的平均能量达到最小［8］。在一个16－QAM星座中每个标记位有4种状态可供选择，4种状态对应4个不同的功率。因此，通过选取合适的标记符号矢量，可以使信息序列的传输能量达到最小［9］。

图1 结合标记位整形的编码调制系统Fig.1 Coded modulation system with sign bit shaping

3 本文算法

本文整形的基本思想和标记符号整形类似，即通过整形找出平均功率最小的信息序列，这种算法是对标记整形算法的扩展。图1中对应的整形码选用LDPC码，假设该LDPC码的校验矩阵为H，生成矩阵为G，那么整形的目的是为了找到最佳的序列Z，其中Z满足以下两个条件:

(1)ZHT=s，其中s是k b的标记位信息;

(2)整形后映射到星座图后的能量α=map(z，a，b，c)是最小的，也就是说，

式中，‖x‖是x的绝对值。

在接收端，我们可以通过S=ZHT恢复出s，由于非标记位abc并没有发生变化，只是映射到了星座图中，所以可以通过一个逆映射直接恢复出abc。

下面我们通过一个简单的例子对该算法进行说明。

假设有如下的校验矩阵:

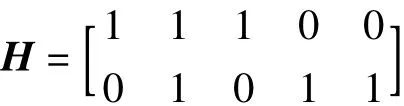
它对应的Tanner图如图2所示。

图2 H矩阵对应的Tanner图Fig.2 Tanner graph of the parity check matrix H

如图2所示，在这个Tanner图中共有3种不同的节点:变化的点代表标记位，校验点代表校验矩阵H中的校验节点，综合节点代表的是信息位。变化的节点Z1、Z2、Z3和第一个校验节点C1的关系满足Z1+Z2+Z3=S1，同理对于校验节点C2，有Z2+Z4+Z5=S2。

假设非标记位的信息是固定的，每个标志位信息是在0和1之间取值，这两种取值对应星座图中的两个点分别有不同的功率。Ei( ui)定义了Zi=Ui时的能量。对应的映射后的能量为

通过上式，这个整形问题可以转化为求

的问题。其中，在QAM星座中，每个坐标的标记符号整形是分开的。

3.1 MPF问题的引入

在文献［10］中已经提到了MPF问题。我们将用具体的标记去解决标记位整形问题。MPF问题首先需要设置一个变量 x= { x1，…，xn}，其中 xi∈{0 ，1}。定义一个局部核心函数 xI，xI={ xi1，…，xim}，其中 I= {i1，i2，…，im}{1 ，2，...，n}，这个函数是x的一个子集。定义x的m个子集xI1，xI2，…，xIm和其对应的局部核心 f1(xI1)，f2(xI2)，…，fm(xIm)，那么整体的核心被定义为

式中，xIi(i=1，…，m)称为局部域。这个MPF问题需要在一个或多个子集xI的基础上计算整体核心F的边缘。也就是说，要计算所有的xIi(其中Ici是Ii的补集):

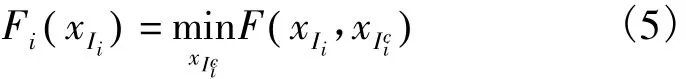
如果所有的局部域能被作为连接树的顶点，那么MPF问题就能用整体分配算法(GDL)求解。

3.2 整形化为MPF问题

我们用图2中的例子来介绍把树形整形化为MPF问题的想法。假设标记位 (z1，z2，…，z5)是MPF问题中的变量，那么局部域和局部核心为

其中，Ei(zi)是按照函数(2)中定义的，χ是根据校验矩阵中校验节点Ci定义的函数:

那么整体核心被看作是

每个局部域{z}i最终有

Fi(ui)中ui的值是根据ZHT=S定义的最小能量编码的i个中最小的一个。由于陪集码字的最小能量是固定的，只需要找到每个节点对应的一个目标函数。如果校验矩阵的Tanner图是一个联结树，这个问题可以用一系列连续算法的顶点GDL算法解决。

3.3 最小和算法

我们通过将Ei=Ei(1)－Ei(0)能量的不同作为Zi的局部核心，介绍一种简化的最小和算法。基于标记位整形的最小和算法，通过树形码来在Tanner图中的各个节点间进行信息传递。一个节点接收到的信息在节点处处理，新的信息则沿着边送出去。假设边界 {e1，e2，…，ed}是与同一个节点相连的边是边接收到的信息，是通过e边送出i的信息，其中i=1，2，…，d，一个信息传递算法指出了一系列节点的过程。针对标记位整形，这个算法沿用连续方案，从最深的变量节点到根节点，其中根节点只有信息输出。针对于图中的树形编码信息的传递方向是

假设一个变量节点 zi有，…个信息进来，那么输出的信息为

假设一个校验节点 Ci有，…，个信息进来，那么输出的信息为

每一个校验节点将累计的输入边位置对应到最小绝对信息上，即。在根节点，我们用下面的公式计算目标函数:

对于根变量节点Z1，判决规则是

只要根节点的值确定了，我们就可以找到最小能量的序列，通过校验节点中储存的变量节点反映射，这些校验节点是从根节点到最深的变量节点。这个和维特比算法里面的反映射很像。

4 实验结果

图3为LDLC码在AWGN信道下的仿真结果。本文仿真采用k=100、n=201的一个校验矩阵，即有k=100个标记位，通过整形后有n=201个码字，编码器的输入信息b采用二进制，即b的元素值取自于－1和1。我们用误码率(BER)和信噪比(SNR)对仿真结果进行描述。根据图1的编码调制系统图，在未编码前，星座图的平均功率为21.333;利用k=100、n=201的检验矩阵进行编码后，平均功率变为 18.826，所以可以得到整形增益为0.528 dB。同时当CER=2时，随着k的增加，编码增益可以达到0.53 dB。在该仿真中没有增加错误控制码，但在实际信道中一般会增加错误控制码，由于错误控制码在信息序列中占的比例很小，所以加入错误控制码后对该算法的编码增益基本没有影响。

图3 AWGN信道下的仿真结果Fig.3 Simulation results on AWGN channel

5 结束语

本文借鉴标记位整形的思想，结合LDPC码的校验矩阵H和Tanner图，通过最小和算法找出功率最小的信息序列，从而达到整形的目的。该算法是在LDLC码进行编码之前对其信息序列进行处理，通过使用LDPC码，使得信息的平均功率得到减少。同时，该算法是针对信息序列本身进行处理，与其他整形方法不同，该算法没有参与LDLC码的编码过程，是一种完全独立的整形方法。仿真证明:整形前后产生了约0.53 dB的整形增益，与Sommer提出的基于下三角矩阵的整形方法相比，该方法具有普遍适用性，是一种有效的整形方法。

本文算法中整形码字采用的是非方阵的LDPC码，由于校验矩阵是非方阵的，输入和输出的码字个数不同，使得输出的码字增加了信息量，起到了整形的目的。而采用方阵LDPC码或是其他码字作为整形码字，将是下一步的研究方向。

［1］ Zhu Lian － xiang，Dai Gai－ rong，Tang Ying.Principles of Low Density Lattice Codes and their Performance Simulation［J］.Journal of Chongqing University of Posts and Telecommunications，2010，22(2):58 －60.

［2］ Sommer N，Feder M，Shalvi O.Low － density lattice codes［J］.IEEE Transactions on Information Theory，2007，54(4):1561－1585.

［3］ 杨海艳.一种构造八环准循环LDLC码的搜索算法［J］.重庆邮电大学学报(自然科学版)，2011，23(5):570－573.YANG Hai－yan.A search algorithm to construct girth－8 quasi－ cyclic LDLC［J］.Journal of Chongqing University of Posts and Telecommunications(Natural Science E-dition)，2011，23(5):570 －573.(in Chinese)

［4］ Yona Y，Feder M.Efficient Parametric Decoder of Low Density Lattice Codes［J］.IEEE Transactions on Information Theory，2009，50(6):366 －370.

［5］ Forney G D.Trellis Shaping［J］.IEEE Transactions on Information Theory，1992，38(2):281－300.

［6］ Erez U，Zamir R.Achieving 1/2 lg(1+SNR)on the AWGN channel with lattice encoding and decoding［J］.IEEE Transactions on Information Theory，2004，50(10):2293－2314.

［7］ Sommer N，Feder M，Shalvi O.Shaping Methods for Low－Density Lattice Codes［J］.IEEE Information Theory Workshop，2009，54(6):238－242.

［8］ Shalvi O，Sommer N，Feder M.Signal Codes［C］//Proceedings of 2003 Information Theory Workshop.Paris，France:IEEE，2003:332－336.

［9］ Paterson K G，Tarokh V.On the existence and construction of good codes with low peak－to－average power ratios［J］.IEEE Transactions on Information Theory，2000，46(9):1974－1987.

［10］ Srinivas A，McEliece R.The Generalized Distributive Law［J］.IEEE Transactions on Information Theory，2000，46(2):325 －343.