一种认知跟踪雷达LFM波形库建立方法*

俞道滨，吴彦鸿，朱卫纲

(1.装备学院信息装备系，北京 101416;2.装备学院光电装备系，北京 101416)

1 引言

2006年，国际著名信号处理专家Simon Haykin首次提出了认知雷达的概念［1］，并在随后发表的多篇文章［2－4］中对认知雷达系统各部分的实现进行了说明。认知雷达将跟踪系统、波形发射系统以及目标场景视为一个闭环的整体，通过对波形的实时调节实现对目标的有效跟踪，提高了雷达的跟踪性能。认知雷达基本结构中，通过感知－行动环路对目标进行检测跟踪是其工作的基本形式，在接收端对环境的“感知”引导发射端采取相应的“行动”。

当前，在认知雷达的行动执行器部分中，研究的重点集中于对认知雷达的发射波形优化。基于信噪比、信息论等准则的波形优化是认知雷达首选的波形优化方案。然而，在波形优化的过程中，求解最优解过程往往比较复杂，而且计算量比较大，可能导致观测间隔内雷达发射机无法及时地发出设计好的波形。因此文献［5－10］提出用建立波形库的方法来优化雷达的发射波形，其基本思想是在跟踪系统中添加一个波形库，最优化选择时跟踪滤波器遍历波形库中的每个波形，并从中选择下一个时刻的发射波形。

A.W.Rihaczek［5］指出了一个比较简单的波形库选择策略，根据模糊函数不同将波形分为4类并对每种信号举例进行了理论研究，指出了不同的表现性。Cochran［6］着重研究了波形库的建立和波形调度算法，对于波形库的建立从信息论的角度提出了由6种波形建立的波形库并分别采用单步调用、多步调用和无调度算法对跟踪性能进行了比对。Savage［7］对机动目标跟踪采用了 IMM的算法通过分数阶傅里叶变换来旋转测量误差椭圆以得到最优波形，考虑了追踪加速目标的波形选择算法，提高了跟踪性能。檀甲甲［8］提出对机动目标采用多项式预测模型建模的思想方法，对最优波形的获得也采用了分数阶傅里叶变换旋转测量误差椭圆的方法。Suvorova［9－10］提出了波形库的优化准则，并从信息论的角度出发，得出LFM波形库和LFM－Rotation波形库在其准则下只需保留最大和最小调频率的结论。

本文综合以上研究成果，提出在认知跟踪的框架内，应用交互多模型(IMM)作为机动目标的模型，综合考虑了目标的多种机动状态，采用线性高斯条件下的最优贝叶斯滤波——卡尔曼滤波的原理，对多次机动的目标进行仿真，验证建立LFM波形库对跟踪性能提升的影响。

2 信号模型

首先建立认知雷达的信号模型，明确雷达信号与目标跟踪算法之间的关系。在接收端应用目前使用较为广泛的匹配滤波器，通过计算最大似然函数从而进行最佳信号检测和最优参数估计。此处假设信噪比足够大，估计误差足够小，那么似然函数的峰值为最大似然估计值，估计误差达到测量噪声的克拉美劳下限(CRLB)，并随着发射信号波形的变化而变化。

假设发射的基带信号为s(t)，则雷达发射的窄带脉冲sT(t)可以表述为

式中，ωc为载波频率，ET为发射脉冲的能量，Re{·}表示取实部。雷达接收信号可以表述为

式中，φ是随机的相移，ER是接收信号的能量，n(t)为基带上零均值的高斯白噪声。参数τ和v分别为目标的时延和Doppler频移。根据雷达测距测速的原理，目标的位移和速度与其时延τ和Doppler频移v存在如下关系

对于接收到的信号，sR(t)通过下变频之后得到基带信号。将此基带信号通过对应的雷达接收匹配滤波器，可以得到其模糊函数

可以看到，模糊函数是有关时延τ和Doppler频移v的二维函数。模糊度函数A(τ，v)最大的值对应的变量(τ，v)，即为理想情况下雷达的接收传感器部分对目标的时延τ和Doppler频移v的测量，根据式(4)求得对目标位移r和速度的测量。

带有波形参数的测量噪声协方差阵设为N(θk)，其与模糊度函数A(τ，v)存在如下关系:

式中，θk为波形参数向量;J为A(τ，v)关于时延τ和Doppler频移v的fisher信息矩阵;J－1即为对时延τ和Doppler频移v无偏估计的CRLB。式(5)建立了雷达信号与目标跟踪之间的联系，为变波形条件下的目标跟踪奠定了基础。

3 交互多模型(IMM)跟踪

目标跟踪滤波算法是认知跟踪的核心部分之一。本文就目标的机动运动进行相应的分析和讨论，此时交互多模型跟踪是一种较优的跟踪算法。IMM算法考虑了运动模型的特点，对多个单独模型跟踪的估计值加权求和，得到组合状态估计，其原理如图1所示。

图1 IMM工作原理结构图Fig.1 Operating principle for IMM structure

交互式多模型算法是一种递归算法，算法的每一个循环过程包括以下几步:输入交互、滤波、模型概率更新和输出综合。设IMM模型转移矩阵为Π，模型i初始模型概率μi(k－1|k－1)，则IMM算法一个采样周期记为 IMM［Mk，Mk－1］，其中 Mk为 k 时刻模型集，Mk－1为k－1时刻的模型集。对任意模型mj∈Mk，具体循环步骤如下。

(1)模型条件初始化

计算预测模型概率μj(k－1|k－1)、混合权重μij、混合估计 Xj、混合协方差 P(k|k)。

(2)模型条件滤波

把上两式得到的滤波结果作为下一时刻与模型mj相匹配的输入变量，然后每个滤波器按照各自的算法进行状态滤波得到各自的状态估计Xj(k|k)及协方差Pj(k|k)。

(3)模型概率更新

似然函数:

概率模型:

(4)组合

计算总体估计X(k|k)和总体协方差P(k|k)。

IMM算法由初始化到最终的组合是一个不断循环的过程，雷达发射信号模型与每个跟踪器建立联系，在波形实时变化过程中对机动目标进行跟踪。由于波形变化的多样性，通过确定一定数量的波形并建立波形库的方法，实现对波形的调用，达到跟踪误差减小的目的。

4 LFM波形库的建立

4.1 波形库构建策略

本文研究的重点是引入认知环路对跟踪性能的提升，波形库作为行动执行器的组成部分，提供优化的发射波形。因此，制定适合发射端的波形选择策略是构建波形库的基础。

假设z0是感知－行动环路的初始条件，认知从这个最初的观测值开始。发射端通过计算代价函数(由接收端输出计算得到)产生下一时刻发射的最优波形参数向量，并随后获得了新的观测值z1，得到该循环环路为 z0→θ0→…→zk→θk。

如果按照上述的行动－反应环路来设计，其初始条件就应该是波形参数θ0，而不是z0。认知雷达在发射单一波形后，通过处理回波得到新的观测值zk，发射端仍通过计算代价函数来获得下一时刻发射的波形参数向量θk，其循环环路为θ0→z1→…→θk－1→zk。

起始点的设定对于波形库的构建策略具有一定的影响，下文中采用第一种循环方式作为发射波形的选择策略，即假设目标的初始状态已知，在获得目标的量测值z1后对波形进行优化。

就目标跟踪而言，最优的波形选择为使得测量误差椭圆与估计误差的先验误差椭圆正交的波形，然而接收到的测量误差椭圆对于多个模型而言，所得到的波形参数是不同的。对于应用波形库的情况下，设定一定间距的旋转角度取一组LFM信号，通过选择设定不同的先验估计误差，在多模型交互时对各模型下选择的优化波形进行融合，在波形选择准则下确定最终的优化波形。波形优化及波形库的构建如图2所示。

图2 波形优化及波形库的构建示意图Fig.2 Waveform optimizing and waveforms library's construction

考虑与先验误差相关的LFM调频率参数，取s(t)=s0(t)exp( jbt2)，应用分数阶傅里叶变换(Fr-FT)调整设定调频率参数下的旋转角度，即可建立一个LFM波形库。

满足|S|=1的归一化条件下，不同的调频参数b和不同的FrFT旋转角度对应的变换矩阵为

4.2 波形选择准则

波形选择准则是在跟踪过程中选择波形的依据，文献［8］重点研究了这一问题，对IMM框架下的多种波形选择准则展开讨论。在认知跟踪雷达中，我们从信息论的角度描述其每一个反馈环路，选择使目标动态模型不确定性最小的波形。对于单步调用的策略，该准则可以定义为最小化模型概率分布熵的波形选择准则，即最大化各模型与观测值之间的互信息，两者的差值表达式为

其中:

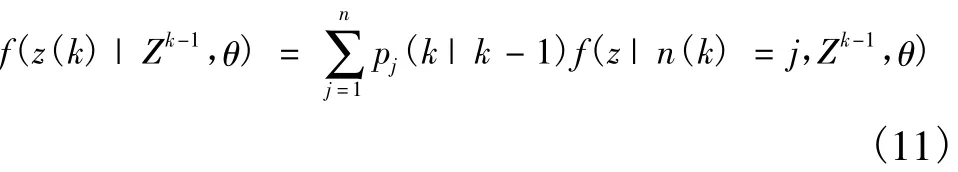
其中，f(z|n(k)=j，Zk－1，θ)为第 k 次的预测概率密度，在式(14)中给出。且考虑到pj(k|k)与波形相关，同时将 f(z(k)|Zk－1，θ)近似为高斯分布，与预测概率密度相同，进一步运算得

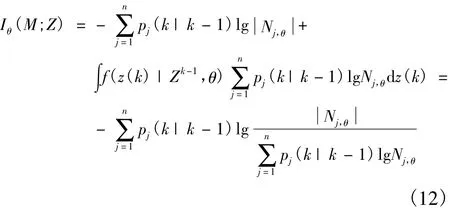
为获得最大信息量，可令熵值表达式最小，即波形选择准则表达式为

5 仿真验证与分析

对于真实目标，其在实施机动前会有一定的缓冲，并在一次运动过程中的机动次数较少。此处考虑一个距离雷达1.5 km处以初速度350 km/h运动的点目标，其在雷达的观测范围内作多次机动，这样可以较为明显地体现出引入波形库的优势。

目标跟踪的距离－速度变化如图3所示。

图3 机动目标运动变化示意图Fig.3 Variation of maneuvering target in motion

在由单个观测站对目标运动的距离和速度进行观测，观测间隔Δt=2，相应的跟踪方程参数为

目标运动过程中最大的加速度amax=50，设定在各模型中，ai为 50、20、0、－20、－50，i=1，2，…，5，模型的初始概率均为0.2，控制模型转化的马尔科夫链的转移概率矩阵为

根据以上波形库构建原则，得到了具有不同数量波形数的波形库，并在此条件下进行仿真验证。

为了便于对各种情况进行对比，采用滤波的积累误差:

按照上述设定进行100次蒙特卡罗仿真，获得了对目标距离和速度跟踪误差的结果如图4所示。对仿真结果分析可知，单波形和双波形在距离方向上的跟踪误差相近，而双波形由于在调频率上具有可选择性，在多普勒速度估计上具有优势，可以在速度估计上获得相对较小的误差。对于六波形和十波形的波形库，其在距离和速度上的误差较无波形库的情况均明显减小，波形库在跟踪中实时调用波形发挥了一定的作用。而在六波形的基础上为了增加精度而加入的波形并未体现出明显的优势，六波形与十波形在距离跟踪精度上的差别相对较小，在速度跟踪中两者的误差近乎相等。

图4 距离与速度跟踪误差对比图Fig.4 Comparison of range and speed tracking errors

仿真中，根据波形选择准则，在所建立的波形库内对LFM波形执行的选择策略及仿真中平均每次所用的时间如图5所示。不同类波形库下调时间对比如表1所示。

图5 波形选择策略Fig.5 Waveform selection strategy

表1 不同类波形库下调用时间对比(平均)Table 1 Comparison of time cost in four libraries(average)

分析图5波形库自适应的调用过程可知，在目标与雷达之间的距离相对较远且速度增加时，双波形的变化相对密集，在第150 s左右双波形波形库不断变换选择波形，使速度跟踪误差维持在一个小范围的同时，其在距离向上的跟踪误差有所增大，甚至在末段其距离跟踪精度明显变差，这说明波形数量过少时，其在距离和速度上的跟踪误差无法同时降低。文献［9］也分析了单就对脉冲信号分数阶傅里叶变换角度的优化时对于降低跟踪距离和速度上的误差存在矛盾。因此，应用双参数的调节以及对波形库的引入对两个参数的优化均具有一定的优势。

综合以上图表可以看出，对于具有一定数量的波形库，在发射信号带宽限制下，增加波形数量对于提高跟踪精度的影响不大，而由图5和表1可以看出，十波形在调用时不断变化占用了一定的时间和系统资源，使得系统负载加大。因此，此处选用六波形的波形库具有最优的跟踪性能。

6 结语

本文在认知跟踪雷达的背景下，提出了建立LFM波形库实现对发射波形实时调用的方法。首先，明确了雷达的信号模型，应用交互多模型算法实现对机动目标的跟踪;其次，阐述了认知跟踪中波形库的构建策略，根据信息论设计波形选择准则，以最小化模型选择不确定性为目标推导了准则函数;最后，通过选择不同的调频率参数和分数阶傅里叶旋转角度的组合构成的波形库，对结论进行了仿真验证。在文献［9］研究的基础上，本文考虑了更多机动目标的运动状态，并且仿真了较多数量波形构成的波形库对目标跟踪的影响，而在不同运动模型及不同机动状态下，如何选择一定数量的波形以平衡系统负荷与跟踪精度之间的关系，是下一步研究的重点之一。本文仿真结果表明，通过建立一定数量的LFM波形库，可以达到减小距离和速度的跟踪误差的目的，提高了对机动目标的跟踪性能。

［1］ Haykin S.Cognitive radar:a way of the future［J］.IEEE Signal Processing Magazine，2006，23(1):30 －40.

［2］ Haykin S.Cognitive Dynamic Systems［C］//Proceedings of 2007 IEEE International Conference on Acoustics，Speech and Signal Processing.Honolulu，HI:IEEE，2007:1369－1372.

［3］ Haykin S，Xue Yanbo，Davidson T N.Optimal waveform design for cognitive radar［C］//Proceedings of 2008 42nd Asilomar Conference on Signals，Systems and Computers.Pacific Grove，CA:IEEE，2008:3 －7.

［4］ Haykin S，Zia A，Arasaratnam I，et al.Cognitive tracking radar［C］//Proceedings of 2010 IEEE Radar Conference.Washington DC:IEEE，2010:1467 －1470.

［5］ Rihaczek A W.Radar Waveform Selection－A Simplified Approach［J］.IEEE Transactions on Aerospace and E-lectronic Systems，1971，AES－7(6):1078－1086.

［6］ Cochran D，Suvorova S，Howard S D，et al.Waveform Libraries［J］.IEEE Signal Processing Magazine，2009，26(1):12－21.

［7］ Savage C O，Moran B.Waveform Selection for Maneuvering Targets Within an IMM Framework［J］.IEEE Transactions on Aerospace and Electronic Systems，2007，43(3):1205－1214.

［8］ 檀甲甲，张建秋.跟踪机动目标的雷达波形选择新方法［J］系统工程与电子技术，2011，33(3):515－522.TAN Jia－jia，ZHANG Jian－qiu.New waveform selection approach to tracking maneuver targets［J］.System Engineering and Electronics，2011，33(3):515 －522.(in Chinese)

［9］ Suvorova S，Howard S D，Moran W，et al.Waveform Libraries for Radar Tracking Applications:Maneuvering Targets［C］ //Proceedings of 2006 40th Annual Conference on Information Sciences and Systems.Princeton，NJ:IEEE，2006:1424 －1428.

［10］ Suvorova S，Howard S D，Moran B.Generalized frequency modulated waveform libraries for radar tracking applications［C］ //Proceedings of 2009 Conference Record of the Forty－Third Asilomar Conference on Signals，Systems and Computers.Pacific Grove，CA:IEEE，2009:151－155.