测量船外测数据的四矢量误差分析方法*
2013-08-08傅敏辉伍辉华王旭良
傅敏辉,杨 磊,伍辉华,王旭良
(1.中国卫星海上测控部,江苏江阴 214431;2.飞行器海上测量与控制联合实验室,江苏 江阴 214431)
1 引言
航天测量船是一个运动的平台,海上测量是在动态条件下进行的,船的航行、摇摆、振动、颠簸等都会使船的位置和姿态不断地变化[1]。在航天发射任务中,卫星入轨段的测量一般由测量船独立承担,故判断卫星是否准确入轨时测量船的外测数据质量起着非常重要的作用;同时,当航天器位于远离我国领空一侧而需要依托测量船完成变轨控制甚至定点时,船载站测量精度将在一定程度上决定该航天器变轨控制的精度。随着近几年航天技术的飞速发展,航天测控任务日益密集,航天测量船承担的试验任务需求也由初始轨道段中等精度测量提高到卫星定点的高精度测量,由一箭一星的测量提高到一箭多星的测量,任务需求的变化对测量船测控技术的发展提出了迫切要求。因此,全面系统地研究测量船的误差影响对于测量船适应新形势下的可持续发展具有重要的意义。
2 测量船的主要误差源影响
2.1 设备误差
主要包括设备本身产生的误差、信号传播误差以及跟踪目标过程中产生的误差。
(1)外测设备测量误差[2]
它包括了系统分量和随机分量,主要误差源有频率源的瞬稳、接收机的噪声、各锁相环路VCO的内部噪声、各部件的相位漂移、校零残差、电轴漂移误差、零点对准误差、天线座方位转台不水平误差、轴系正交误差、光电不垂直和光电轴不匹配等。其中光轴不垂直只引起方位误差,光电轴不匹配会引起方位和俯仰角误差。
(2)大气折射修正剩余误差
这属于信号传播误差,虽然在数据处理时已利用实测气象数据进行了大气折射修正,但当目标在低高度时,其剩余误差也可达到百分之几到百分之二十。
(3)动态滞后误差
该项误差是由于目标的运动而产生,它与伺服系统的性能有关,是一种特殊的系统误差。在航天测量船测控中,由于雷达安装的基座随着船摇和船体变形扭动,会导致雷达天线方向随之改变,有时和跟踪目标移动方向相反,这将导致动态滞后误差增大。
2.2 船摇误差
由于风、浪、涌等的综合影响,测量船处于摇摆状态之中。这种误差既有系统分量,又有随机分量。
2.3 船位误差[3]
它基本上是固定偏倚误差,由它引起的目标位置误差也是一种平移偏倚误差,且因地球曲率而被放大,放大系数定义为:k=1+h/re,其中h为目标高度,re为地球半径。在同步轨道,k≈6.6。
2.4 变形误差[4]
由于测量设备的基座与惯导基座之间有一段距离,船体又不是刚体,故因扭转扰曲产生变形误差。这种误差既包括系统分量,也包括随机分量。
3 测量船四矢量误差分析
在分析测量船主要误差源的基础上,为便于后续研究工作的开展,本文提出了对测量船精度影响显著的四矢量误差的概念并进行系统分析。四矢量误差分别指设备误差矢量 Ve1=(ΔR,ΔE,ΔA)、船摇误差矢量 Ve2=(Δkc,Δφc,Δθc)、变形误差矢量Ve3=(Δkb,Δφb,Δθb)和船位误差矢量 Ve4=(Δλ,Δφ,Δh),那么测量船测控任务总误差可表示为e=f(Ve1,Ve2,Ve3,Ve4)。由于国内关于设备误差对测量精度影响的研究成果已经比较全面详实,本文主要根据测量船的特点有重点地研究分析船摇误差矢量和变形误差矢量。
3.1 船摇误差矢量影响分析
船摇数据由航天测量船惯性导航系统测量得到,它反映了船体运动的三维姿态数据,包括艏摇kc、纵摇φc和横摇θc3个分量。船摇数据具有一定的周期性,其模拟数据为

它是一个周期性的三角函数,其中X=(k,φ,θ),X0=(k0,0,0),Tc为船摇周期,Ac为船摇幅值,t为相对时。船摇数据在Δt时间的变化量(即一阶导数)为

该函数也是一个周期性的三角函数。
船摇变化量会对外测数据产生较大的影响,尤其对高轨卫星影响更大,反映到卫星空间位置或对应的地球投影则有来回摆动现象。图1是没有船摇变化量时卫星星下点的理论值。设横摇变化量:幅值 Ac=3°,周期 Tc=24 s,时延 Δt=1 ms;纵摇变化量:幅值3°,周期24 s,时延 Δt=1 ms时,引起的卫星星下点变化如图2所示。该结果是用三角函数模拟船摇值,星下点有周期性的波动,对于实测的船摇数据,会引起星下点的不规律波动。
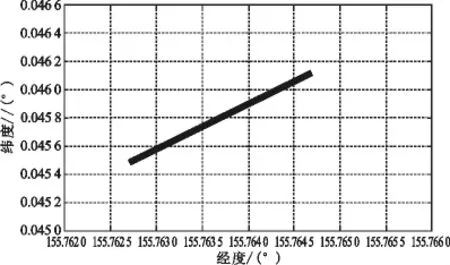
图1 无船摇变化时的星下点Fig.1 Sub - satellite point without ship rocking

图2 船摇变化量引起的星下点误差Fig.2 Sub - satellite point error caused by ship rocking
3.2 变形误差矢量影响分析
由于测量船采用单站定位体制,需要A、E两角度测量,测量设备在航天测量船上是沿艏艉线分散布局的,设备之间有一定的距离,而测量船船体并不是一个刚体,各设备基座间存在变形。在测量船数据处理中需要将设备的测量数据转到以惯导为中心的惯导地平系,因此测量设备基座与惯导基座之间的船体变形量直接影响着角度的测量精度,该变形量包含有艏挠kb、纵挠φb和横扭θb。
为考察变形数据偏差对外测角度和空间位置的影响,采用某理论计算的跟踪性能,不考虑船摇,设定固定的测量数据(测距约40 000 km),初始变形量为艏挠 -10″、纵挠 -15″、横扭 -5″。分别在各个变形量上加入相应的测量偏差,仿真处理结果的偏差情况,详细情况见表1,其中空间位置差指不同情况下计算的卫星空间位置的相对距离。

表1 变形数据偏差对外测角度和空间位置的影响Table 1 Errors of exterior angle and spatial location caused by ship deformation data
由表中可以看出,变形数据偏差5″引入的误差为偏差10″时的一半。从单个测量元素看,横扭偏差5″,空间位置差就达到了900多米。
3.3 四矢量误差影响分析及仿真
在分析船摇误差矢量和变形误差矢量影响的基础上,对测量船四矢量误差的影响进行整体分析。测量船原始测量数据基于测量坐标系,在进行坐标系转换中,会引入测量船四矢量误差的影响,对于地心固连直角坐标系,其X、Y、Z方向的系统差可分别表示为
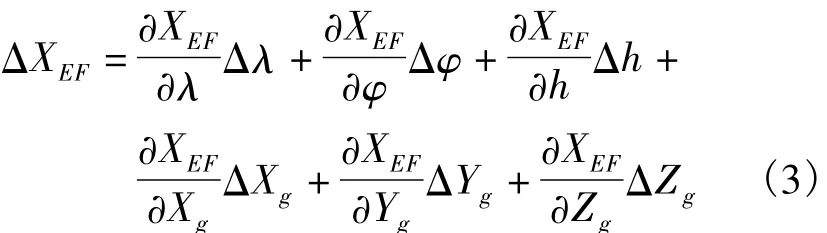
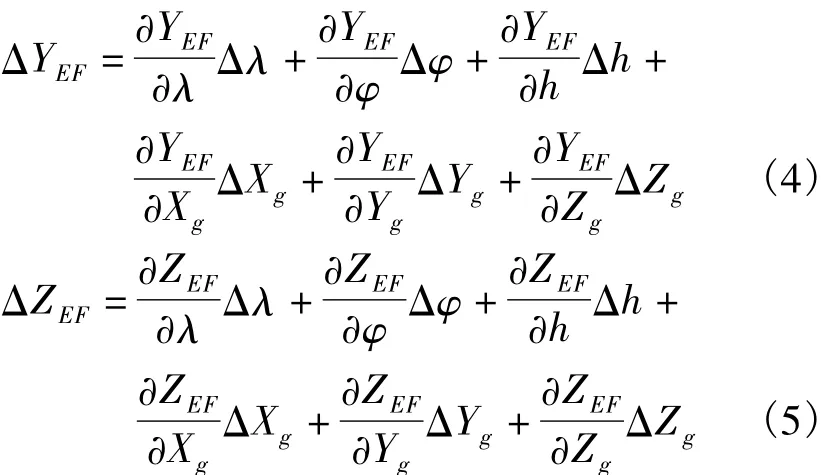
其中,(ΔXg,ΔYg,ΔZg)为惯导地平系下 X、Y、Z 方向的系统差:
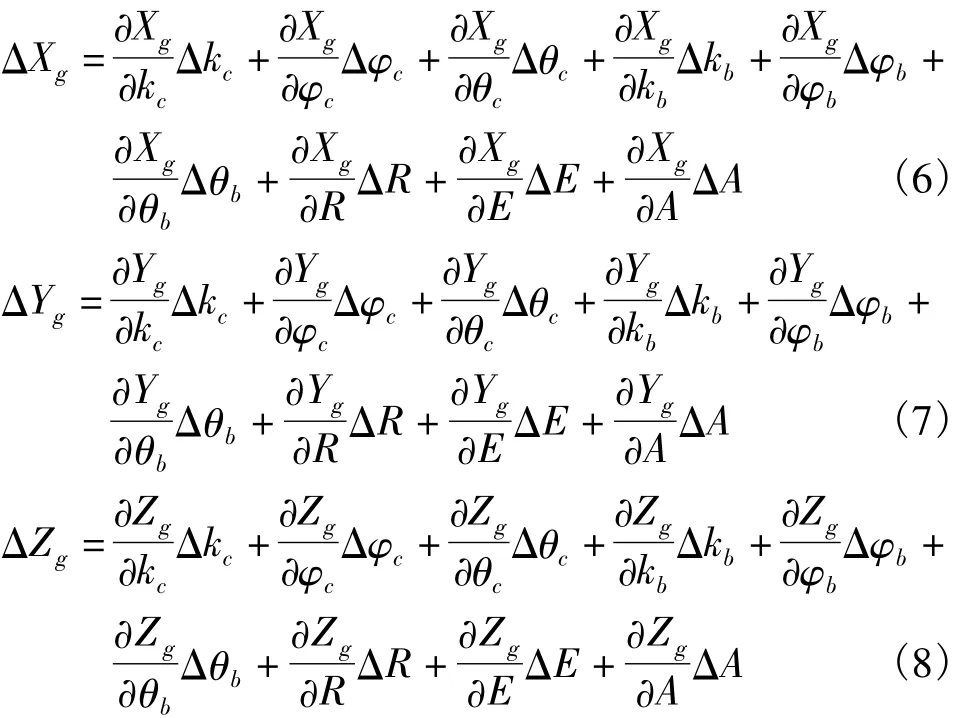
上述偏导数可根据测量船坐标转换公式求得,如惯导地平系X、Y、Z对船摇的偏导数为

其中,Kc、Ψc、Θc为船摇修正的转换矩阵,R、E、A 为外测设备测元,X0、Y0、Z0为外测设备在惯导地平系中的位置。
在上述误差传播公式的基础上,开展了仿真计算。以船载测量设备的校飞精度、船姿船位系统的设计精度作为四矢量的误差量,仿真分析测量船四矢量误差对卫星定位结果的影响。设该卫星测距值约21 000 km,四矢量误差传递到地心固连系中X、Y、Z 3个分量的系统误差如表2及图3~6所示。

表2 四矢量误差对地心固连系影响Table 2 Errors of geocentric coordinate system component caused by four-vector-error
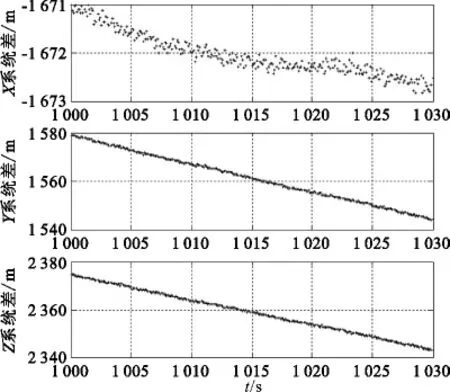
图3 设备误差矢量对地心固连系各分量的影响Fig.3 Errors of geocentric coordinate system component caused by instrumentation measurement error
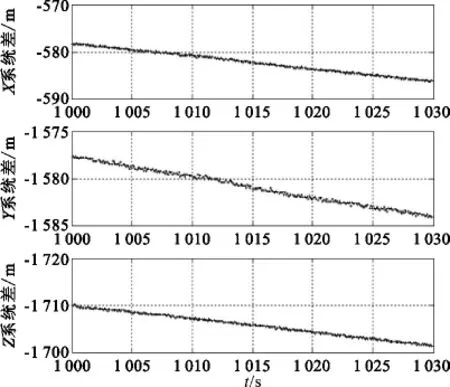
图4 船摇误差矢量对地心固连系各分量的影响Fig.4 Errors of geocentric coordinate system component caused by ship rocking measurement error
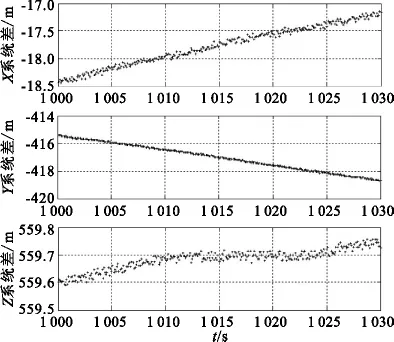
图5 变形误差矢量对地心固连系各分量的影响Fig.5 Errors of geocentric coordinate system component caused by ship deformation measurement error

图6 船位误差矢量对地心固连系各分量的影响Fig.6 Errors of geocentric coordinate system component caused by ship position measurement error
4 测量船四矢量误差应用
为验证四矢量误差的影响,我们还通过事后数据处理软件进一步验证了四矢量误差的影响分析结果。具体方法为:根据标校和校飞结果确定测量船某设备的四矢量误差指标,以某次任务的原始数据为基准数据,依次在基准数据上加四矢量误差,通过四矢量误差的传递公式计算出理论误差,同时用事后数据处理软件处理加误差的测量数据并统计出误差,比较结果如表3所示。该结果表明,四矢量误差的理论分析与实际处理结果的一致性很好。
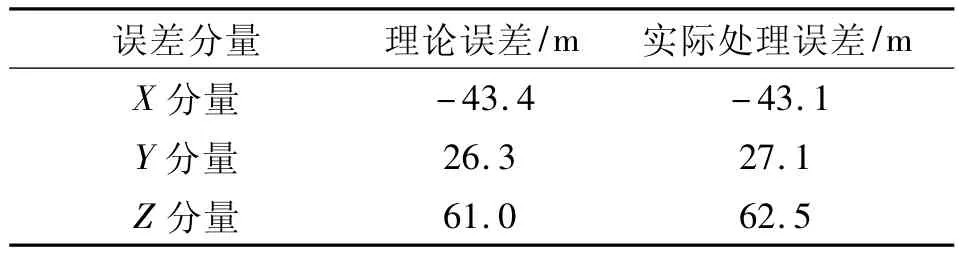
表3 四矢量误差比较结果Table 3 Match result of four-vector-error
在某次高精度要求的卫星发射试验任务中,测量船采用基于四矢量误差的系统控制法对测量船的测量精度进行了系统反馈式控制:利用战前跟星精度检验法对船载测控设备进行精度检验,如果存在精度问题,根据四矢量误差对测量精度的影响关键度,迅速定位故障原因,节省排查问题的时间和资源。实际应用中,跟踪某两颗过境卫星时,测距与设备的精度指标误差偏大,其中跟踪卫星甲测距系统差达188 m,随机差为15 m,跟踪卫星乙测距系统差达140 m,随机差为13.5 m,与设备误差矢量影响关键度吻合,因此经反馈至设备端排查,发现为高轨时测距的时标修正完成后时间取齐不当引起。经对时间取齐方法进行改进,解决了测控设备测距误差偏大的问题,有效提高了任务的测量精度。
5 结论
与陆基设备相比,测量船误差影响因素多,系统稳定性相对较差。本文针对测量船的特点,对影响船载外测数据精度的四矢量误差进行了研究与分析。结果表明,设备本身的测量误差仍占据主导因素,船摇测量误差次之,变形测量和船位测量的误差处于较小量级,并通过实际应用进一步验证了四矢量误差分析的准确性和实用性。
[1] 李晓勇,张忠华.航天测量船船摇数据特性分析[J].中国惯性技术学报,2006,14(3):27 -30.LI Xiao-yong,ZHANG Zhong-hua.The analysis of Swaying Data for Instrumentation Ship[J].Journal of Chinese Inertial Technology,2006,14(3):27 -30.(in Chinese)
[2] 王德纯,丁家会,程望东.精密跟踪测量雷达技术[M].北京:电子工业出版社,2006.WANG De - chun,DING Jia - hui,CHENG Wang -dong.Precision Tracking& Measuring Radar Technology[M].Beijing:Publishing House of Electronics Industry,2006.(in Chinese)
[3] 康德勇,李晓勇,王旭良.船位误差对外弹道测量及定轨精度的影响[J].电讯技术,2010,50(9):106 -109.KANG De- yong,LI Xiao- yong,WANG Xu - liang.Influence of Ship's Position Error on Exterior Trajectory Measurement and Orbit Determination[J].Telecommunication Enginnering,2010,50(9):106 - 109.(in Chinese)
[4] 李晓勇,张忠华,何晶.船体变形对航天测量船外弹道测量的影响[J].飞行器测控学报,2006,25(3):7 -12.LI Xiao - yong,ZHANG Zhong - hua,HE Jing.The Effects of Spacecraft TT&C Ship's Deformation on its Outer Trajectory Measurement Data[J].Journal of Spacecraft TT&C Technology,2006,25(3):7 -12.(in Chinese)
