非正侧视机载雷达一种改进的多普勒频移算法

赵 军，李海燕，赵建洋

ZHAO Jun1,LI Haiyan2,ZHAO Jianyang3

1.空军第一航空学院，河南 信阳 464000

2.郑州铁路职业技术学院，郑州 450052

3.淮阴工学院，江苏 淮安 223003

非正侧视机载雷达一种改进的多普勒频移算法

赵 军1，李海燕2，赵建洋3

ZHAO Jun1,LI Haiyan2,ZHAO Jianyang3

1.空军第一航空学院，河南 信阳 464000

2.郑州铁路职业技术学院，郑州 450052

3.淮阴工学院，江苏 淮安 223003

非正侧机载雷达的杂波分布随距离变化而变化，各距离单元的杂波分布不再满足独立同分布条件，导致统计型STAP处理器性能下降。多普勒频移（Doppler Warping，DW）算法沿主波束方向对杂波非均匀进行了补偿，但在其余方向上杂波非均匀依然存在，因而性能较差。提出了一种改进的非正侧视机载雷达杂波抑制算法——修正的多普勒频移法（Modified Doppler Warping，MDW），先通过多普勒频移法使各距离单元的杂波谱在主波束方向重合，再沿多个多普勒通道使参考单元和检测单元的杂波谱保持一致，进一步消除非正侧视机载雷达的杂波非均匀程度。仿真结果表明，与原有方法相比，该方法的杂波抑制性能有明显提高，且运算量增加不多，是一种具有工程应用价值的方法。

非正侧视阵列；机载雷达；多普勒频移；杂波抑制；空时自适应处理

1 引言

传统的统计型STAP算法都是基于正侧视天线阵列，此时，杂波谱在角度-多普勒平面内呈直线分布，并且不随距离变化而变化，即在距离维是均匀的。因此，可以采用相邻距离单元平均的方法来估计待检测单元的杂波协方差矩阵，从而使STAP处理器性能最优。非正侧条件下，天线阵列轴线与载机航向不一致，杂波谱在角度-多普勒平面内不再呈直线分布，并且随距离变化而变化，即杂波是非均匀的。此时，不能再用相邻距离单元平均的方法来估计待检测单元的杂波协方差矩阵，否则，由于各距离单元的杂波谱在角度-多普勒平面不重合，直接平均将造成杂波谱展宽严重，由此得到的自适应权适量无法在待检测单元形成有效的杂波抑制凹口，不仅不能将待检测单元的杂波有效抑制，而且有可能把靠近主杂波的慢动目标当做干扰滤除。

减小非正侧视条件下杂波距离依赖性导致非均匀的STAP方法主要有四种：（1）杂波补偿算法。主要有多普勒频移法（Doppler Warping，DW）[1-2]，以及Himed等提出的角度-多普勒补偿（Angle Doppler Compensation，ADC）法[3-4]。DW算法将参考单元杂波沿多普勒频率方向平移，使得补偿后各距离单元杂波谱在待检测单元主波束方向重合。ADC算法属于二维平移，将参考单元杂波谱中心沿角度-多普勒方向移动到待检测单元杂波谱中心的位置，从而使得各参考单元与待检测单元的杂波谱中心重合。（2）尺度变换法[5-6]。该方法根据杂波的空时耦合关系将参考单元的杂波平移到待检测单元位置，但实现较复杂，而对误差敏感。（3）基于导数更新（Derivative Based Updating，DBU）的方法[7-8]。该方法假定权矢量是距离的一次函数，通过对样本数据进行扩展，结构简单，且不受距离模糊和多普勒模糊的影响。但其假设前提与杂波分布特性不完全相符，性能较差，而且训练样本数目和计算量都急剧增加。（4）参数估计法[9-10]。该方法通过相邻距离单元的杂波数据来估计杂波散射系数，进而预测待检测单元的杂波协方差矩阵，但其性能受训练样本的影响较大。

本文提出了非正侧阵列一种改进的杂波距离依赖补偿方法——修正的多普勒频移（Modified Doppler Warping，MDW）法。该方法首先通过DW法预处理，使得各距离单元杂波谱在主波束方向重合，以减少主波束方向的杂波非均匀，对于其余方位的杂波非均匀，再沿多个多普勒方向使参考单元和检测单元的杂波谱保持一致，从而进一步减小其余方向的非均匀程度。

2 非正侧视阵列杂波特性

均匀线性阵列机载雷达结构如图1所示，载机以速度v沿平行于X轴正向的水平方向飞行，天线轴线与速度v的夹角（阵列偏置角）为α，杂波散射体与天线轴线和速度v的夹角分别为 β和ψ，仰俯角和方位角分别为θ和φ，杂波散射体的多普勒频率 fd和空间频率 fs分别为：

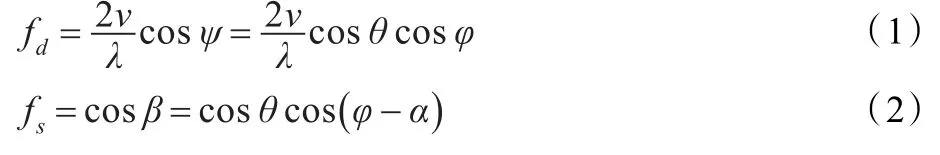
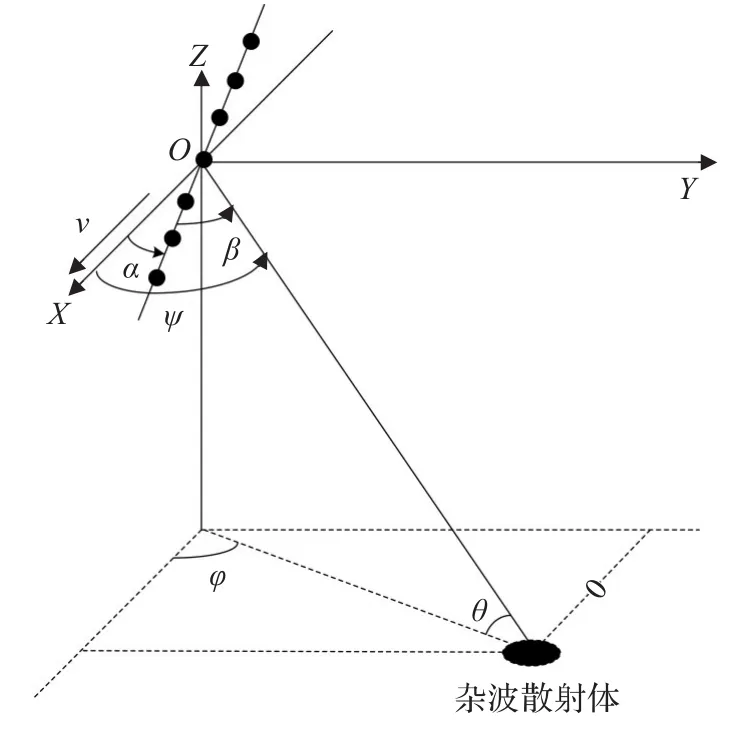
图1 均匀线性阵列天线与杂波散射体几何关系图

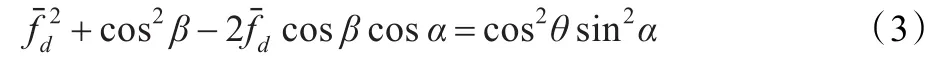
图2给出了载机高度H=8 km，雷达斜距分别为10 km、15 km、40 km和400 km条件下，杂波谱的空时分布图。

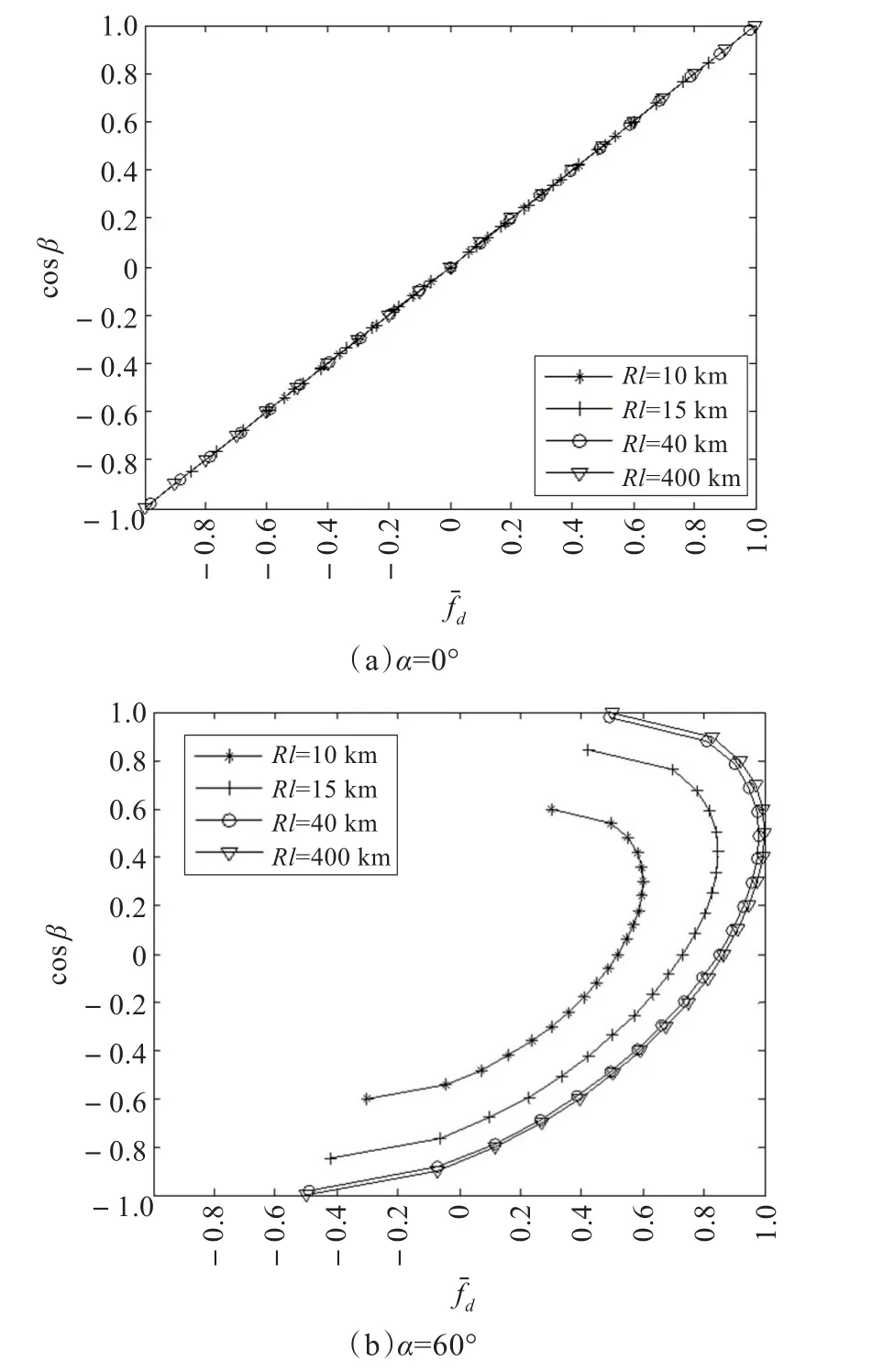
图2 均匀线性阵列杂波谱空时分布图

由图2可以看出，正侧视条件下，即α=0°时，杂波谱分布与距离无关，不同距离处杂波谱的空时分布相同；而非正侧视条件下，即α≠0°时，杂波分布与距离有关，不同距离处杂波谱的空时分布不同，近距离处杂波谱变化剧烈，远距离处变化趋于缓慢直至收敛，杂波分布在距离向是非均匀的。此时，采用相邻距离单元平均的方法来将导致杂波谱严重展宽，由此得到的自适应权适量无法在待检测单元形成有效的杂波抑制凹口，统计型STAP处理器性能严重下降。

3 多普勒频移（DW）法

DW算法[1-2]的基本思想：给定某个波束指向，根据杂波的空时耦合关系式（3）计算出该方向各距离单元的多普勒频率，然后将参考单元的杂波谱沿多普勒方向平移，使得平移后在该方向参考单元杂波的多普勒频率和待检测单元的多普勒相同，从而减小杂波谱展宽程度，以降低杂波非均匀性，对经过补偿后的数据再用常规的STAP方法处理。由于目标检测通常在主波束内进行，DW算法一般沿主波束方向进行多普勒平移。

假定主波束指向的空间锥角为β，设待检测单元为第0单元，从其左右两侧各选取L个距离单元数据Xl作为训练样本，第l个单元的补偿因子，对于 β方向，第l单元与第0单元归一化多普勒频率之差为：

其中：

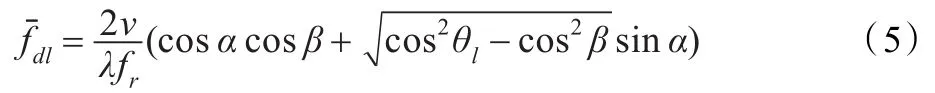
式中，cosθl为第l个距离单元对应的仰俯角，l=-L，…，-1，0，1，…，L。

第l个单元对应的补偿因子：

式中：

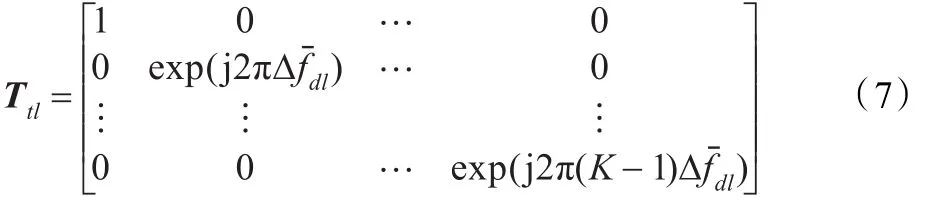
IN是N阶单位矩阵。

经过DW补偿后的第l个单元的数据：

阵列偏离角α=60°时，经DW算法补偿后杂波谱空时分布如图3所示。

经过DW处理后，各距离单元杂主波束方向重合，减小了杂波距离维的非均匀程度。但非正侧视条件下，在整个角度-多普勒平面内各距离单元的杂波分布都是不同的。DW法仅对主波束方向的杂波非均匀进行了补偿，而在其余方位仍存在着非均匀。为进一步减小杂波非均匀程度，需要改善旁瓣方向的杂波非均匀。

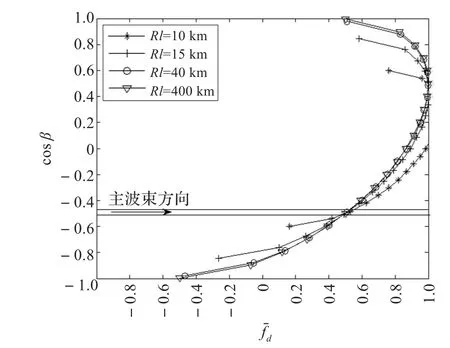
图3 DW算法补偿后杂波分布图（α=60°）

4 修正的多普勒频移（MDW）法

MDW算法的基本思想：对于经过DW补偿后的样本，为减小旁瓣方向的杂波非均匀，在主波束对应的多普勒频率中心两侧各取多个多普勒通道，在各多普勒方向，将参考单元的杂波谱沿角度方向平移，使得参考单元的空间角与待检测单元的空间角相同。由于除了谱中心外还在多个多普勒方向使得参考单元与待检测单元的杂波谱保持一致，因此，与DW法相比，MDW法进一步减小了杂波非均匀程度。

将经过DW法处理后的样本数据 XDW，l转化为一N×K维矩阵，并沿列向量作FFT，得矩阵X′DW，l。

假定在杂波谱中心两侧各取P个多普勒通道，由方程（3），第 p个多普勒方向对应的空间频率为：

Fp表示第 p个多普勒通道的中心频率，p=-P，…，-1，1，…，P，F0=fd，0,l=-L，…，-1，0，1，…，L。

对第l个单元进行补偿时，第 p个多普勒单元，空间频率补偿量为：

该距离单元的补偿因子：

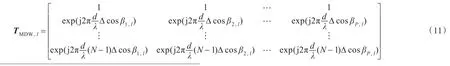
经多空间角补偿后的样本矩阵：

式中“⊙”表示Hadmard内积。

将矩阵X′MDW，l沿列向量作IFFT，并将其转化为NK×1维样本数据XMDW，l，对经过MDW法补偿后的数据再采用常规统计型STAP方法进行处理，把这种先经过DW处理再进行多空间角补偿的方法记为MDW法，其原理如图4所示。

图4 MDW法原理图

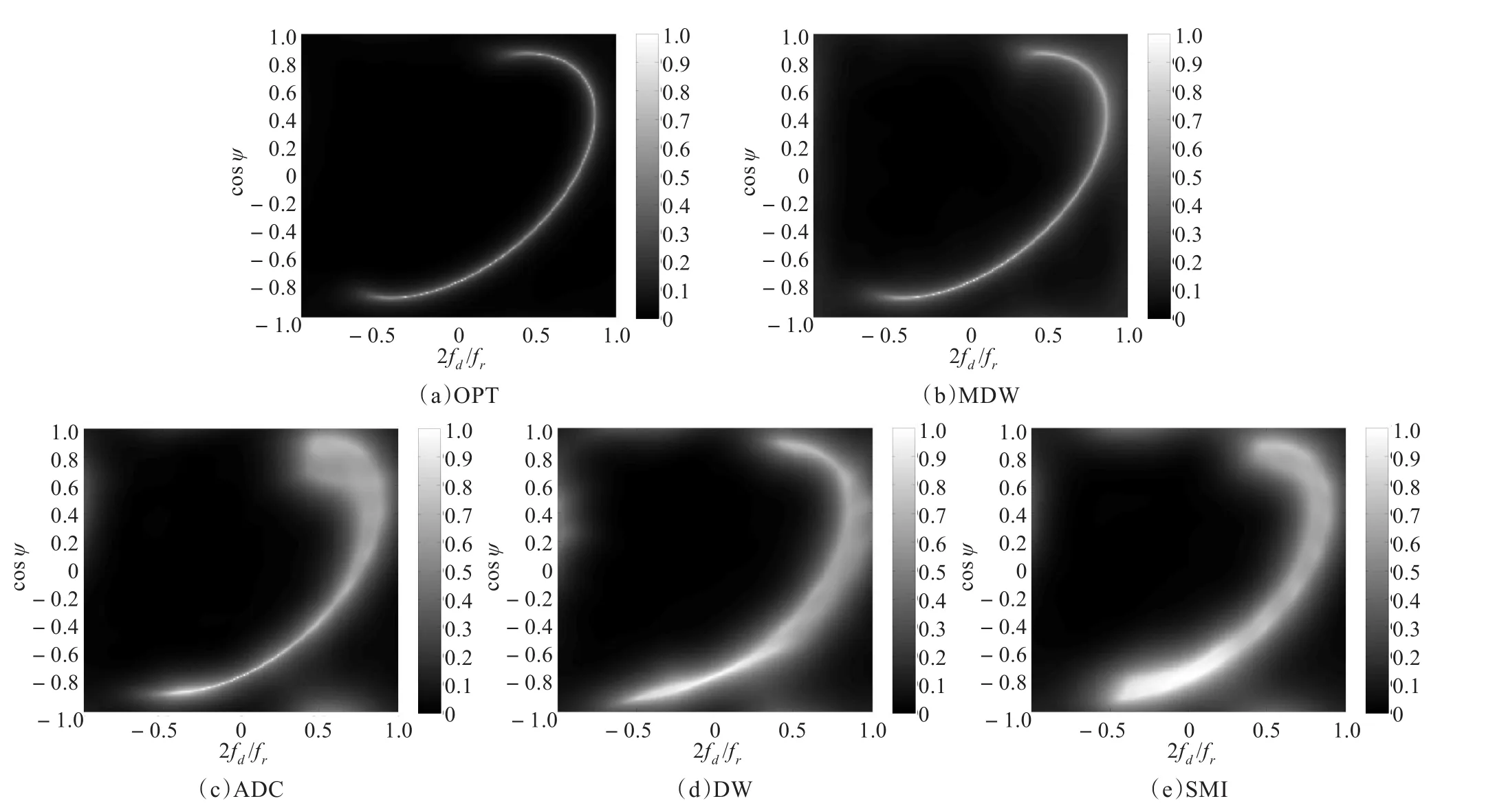
图5 非正侧视阵列杂波补偿STAP算法杂波谱空时分布比较图

MDW算法的步骤可以归纳如下：

（1）采用DW算法对第l个单元的数据Xl进行补偿，得到补偿后的数据XDW，l；

（2）将NK×1维矢量XDW，l转化为一N×K矩阵，并沿列向量作FFT；

（3）在多普勒中心 fd0两侧各取P个多普勒单元，并计算出参考单元和待检测单元在各多普勒方向对应的空间频率之差Δ cosβp，l，构造补偿因子矩阵TMDW，l；

（4）TMDW，l与转化后的矩阵X′DW，l作Hadamard内积，得补偿后的矩阵X′MDW，l；

（5）对矩阵 XMDW，l沿列向量作IFFT，并将其转化为NK×1维矢量XMDW，l。

5 仿真研究

仿真参数为：N=8，K=8，载机高H=8 000 m，载机速度v=130 m/s，雷达工作波长 λ=0.23 m，距离环宽度ΔR=75 m，输入单元杂噪比CNR=50 dB，待检测单元雷达斜距Rs=12 km，训练样总本数2L=128，对补偿后的样本数据，采用3DT法进行降维处理[11]。图5给出了最优处理器（OPT）、MDW法、ADC法、DW法和全空时处理（SMI）[12]杂波谱空时分布比较图；图6给出了非正侧视条件下，杂波补偿STAP算法的改善因子（Improve Factor，IF）[12]比较图，其中MSAC算法中多普勒通道数2P=8。

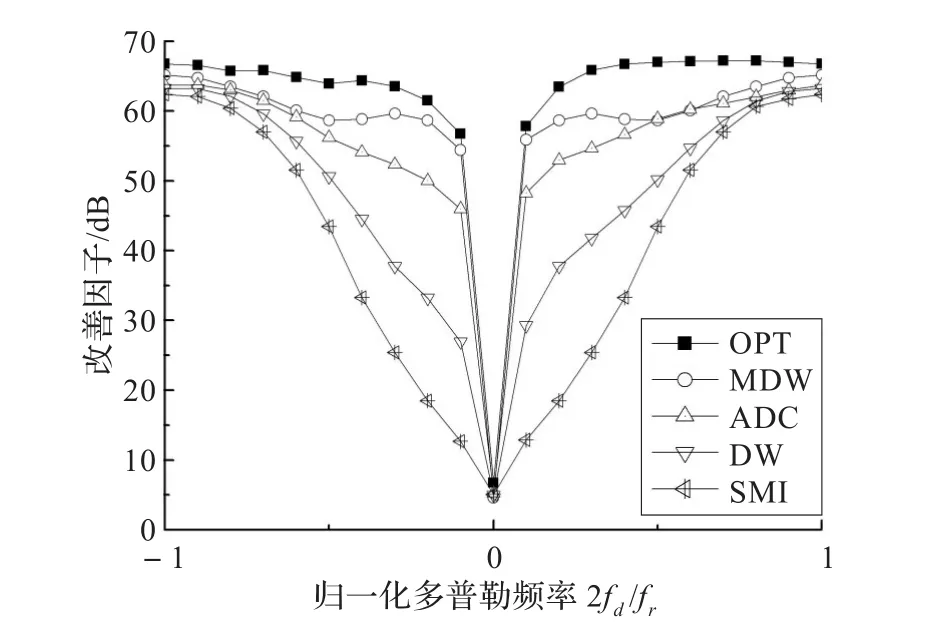
图6 非正侧视阵列杂波补偿STAP算法改善因子比较图

由图5（a）～（e）可以看出，非正侧视条件下，由于各距离单元杂波谱的空时分布不同，相邻距离单元样本直接平均的方法导致杂波谱展宽严重，从而导致STAP处理器杂波抑制性能，特别是主瓣杂波抑制性能严重下降。经补偿处理后，杂波的非均匀程度有不同程度的改善，各距离单位杂波相似程度提高，杂波谱明显“变窄”。由图5和图6可以进一步看出，由于MDW算法在多个多普勒通道对杂波的非均匀进行了补偿，性能明显好于仅对一个方向进行补偿的ADC算法和DW算法，MDW算法的改善因子比DW算法平均提高10.02 dB，比ADC算法平均提高2.92 dB；与DW算法相比，MDW增加了矩阵作Hadamard内积和FFT及IFFT的过程，运算量增加不多，但性能与DW算法相比却有较大提高。因此MDW算法是一种有效可行的杂波非均匀补偿方法。表1和表2给出了MDW、DW和ADC三种补偿算法的训练样本数和运算量的比较。

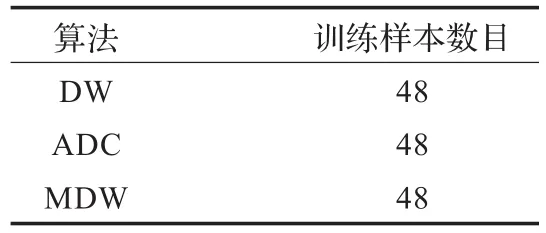
表1 非正侧视杂波补偿STAP算法训练样本数目比较

表2 非正侧视杂波补偿STAP算法运算量比较

6 结论

非正侧视条件下，机载雷达的杂波分布随距离变化而变化，各距离单元杂波不再满足独立同分布条件，统计型STAP处理器的性能急剧下降，为此提出了一种多空间角补偿方法以改善非正侧视机载雷达杂波的非均匀程度。本文方法先采用DW处理，使得各距离的杂波谱在主波束方向重合，然后在多个多普勒方向使参考单元和待检测单元的杂波谱保持一致。仿真结果表明，此方法与现有的杂波补偿方法相比，杂波抑制性能有明显提高，且运算量增加不多，是一种有工程应用价值的方法。

[1]Kogon S M，Zatman M.Bistatic STAP for airborne radar systems[C]//ProcoftheASAPWorkshop.Lexington，MA，USA：MIT Lincoln Laboratory，2001.

[2]龚清勇，朱兆达.非正侧视机载雷达杂波抑制算法研究[J].电子与信息学报，2009，31（4）：977-980.

[3]Himed B，Zhang Y H，Hajjari A.STAP with angle-Doppler compensation for bistatic airborne radar[C]//Proc of the IEEE National Radar Conf，Long Beach，CA，USA，2002：311-317.

[4]Jaffer A G，Ho P T，Himed B.Adaptive compensation for conformal array STAP by configuration parameter estimation[C]// Proc of the IEEE National Radar Conf，Verona，NY，USA，2006：731-736.

[5]Lapierre F D，Droogenbroeck M V，Verly J G.New methods for handling the dependence of the clutter spectrum in non-sidelooking monostatic STAP radars[C]//Proc of the IEEE Acoustics，Speech，and Signal Processing Conf，Hong Kong，China，2003：73-76.

[6]杨博，周一宇，黄知涛.距离模糊条件下双基地STAP的距离独立性补偿[J].电子学报，2010，29（3）：555-561.

[7]Zatman M.Circular array STAP[J].IEEE Trans on AES，2000，36（2）：510-517.

[8]李明，廖桂生.基于导数更新的双基机载雷达杂波距离依赖性补偿方法[J].电子与信息学报，2009，31（9）：2059-2064.

[9]Jaffer A，Himed B，Ho P T.Estimation of range-dependent clutter covariance by configuration parameter estimation[C]// ProcoftheIEEE Int RadarConf，Arlington，VA，USA，May 2005：596-601.

[10]Nert X，Acheroy M，Verly J G.Maximum likelihood range dependence compensation for STAP[C]//Proc of the IEEE Int Conf on Acoustics，Speech and Signal Processing，Honolulu，Hawaii，USA，April 15-20，2007，2：913-916.

[11]Fa R，Lamare R C，Wang L.Reduced-rank STAP Schemes for airborne radar based on switched joint interpolation，decimation and filtering algorithm[J].IEEE Trans on SP，2010，58（8）：4182-4194.

[12]Klemm R.Principle of space-time adaptive processing[M]. London：IEE Press，2002.

1.The First Aeronautic Institute of Air Force,Xinyang,Henan 464000,China

2.Zhengzhou Railway Vocation and Technical College,Zhengzhou 450052,China

3.Huaiyin Institute of Technology,Huaian,Jiangsu 223003,China

The clutter distribution of airborne radar with non-sidelooking array antennas varies with ranges and samples in different range gates are not independent identically distributed vectors,so that the statistical Space Time Adaptive Processing （STAP）methods degrade.Traditional Doppler Warping（DW）method does compensation only in the mainlobe direction and there is still large clutter dispersion in the directions of sidelobe,so it can only alleviate the clutter nonhomogeneity in some degree.An improved clutter suppression method for non-sidelooking airborne radar,namely Modified Doppler Warping（MDW）method,is proposed.This improved method involves in a preprocessing with DW method to bring clutter spectrum of different range gates together in the mainlobe and subsequently clutter compensation to accomplish space angle of different range gates alignment at multiple Doppler bins.Simulation results show,compared with Doppler warping algorithm,the proposed method can further reduce the clutter nonhomogeneity of non-sidelooking array and performs significantly better than DW algorithm while the computation load is almost equivalent to it.

non-sidelooking array;airborne radar;Doppler Warping（DW）;clutter suppression;Space-Time Adaptive Processing（STAP）

A

TN951

10.3778/j.issn.1002-8331.1108-0381

ZHAO Jun,LI Haiyan,ZHAO Jianyang.Improved Doppler warping method for airborne radar with non-sidelooking array.Computer Engineering and Applications,2013,49（7）：151-155.

航空科学基金（No.20102052024）；江苏省高校项目（No.JHB2011-59）。

赵军（1974—），男，博士，讲师，研究方向：空时自适应处理和阵列信号处理；李海燕（1973—），女，讲师，研究方向：网络安全。E-mail：happyzj112@163.com

2011-09-02

2011-12-23

1002-8331（2013）07-0151-05