基于强跟踪滤波器的交互式多模型算法

张 莹，贺丰收，郑世友

基于强跟踪滤波器的交互式多模型算法

张 莹，贺丰收，郑世友

针对传统的EKF-IMM算法鲁棒性较差等问题，提出了一种基于强跟踪滤波器（STF）的交互式多模型算法。该算法通过引入强跟踪滤波器（STF）的渐消因子，实现了对滤波器增益的实时调节，从而提高了系统对机动目标的自适应跟踪能力和跟踪精度。仿真结果表明，在目标不发生机动时，该算法和EKF-IMM算法的跟踪效果相近，在目标发生强机动时，该算法在径向速度和方位角的跟踪精度要优于EKF-IMM算法；提出的算法具有更优的机动目标跟踪性能。

机动目标跟踪；交互式多模型；强跟踪滤波器；渐消因子；自适应“当前”统计模型

1 引言

目标跟踪算法为了获得较高的跟踪精度，大多采用交互式多模型（IMM）算法，这种算法在多模型算法的基础上考虑多个模型的交互作用，以此得出目标的状态估计[1]。在实际应用中，由于测量值多在极坐标系下获得，目标运动模型往往用直角坐标系描述，两者间关系是非线性的，因此IMM在应用中主要是基于扩展卡尔曼滤波（EKF）算法。随着扩展卡尔曼算法研究和应用的深入，其缺点也日益明显，如扩展卡尔曼滤波器自身鲁棒性较差，容易导致模型受参数影响较大等问题[2]。

考虑到强跟踪滤波器（Strong Tracking Filter，STF）的鲁棒性强，能自适应跟踪机动目标等优点[3]，本文提出了一种基于强跟踪滤波器的交互式多模型算法。通过在滤波器中引入STF渐消因子，可以根据目标机动情况，动态地调节滤波器增益矩阵，增强了系统对目标机动的自适应能力。仿真结果表明，与EKF-IMM算法相比，本文提出的算法对机动目标具有更优的跟踪性能。

2 目标运动模型

（1）CV模型和CA模型

CV模型的一维离散状态方程为：

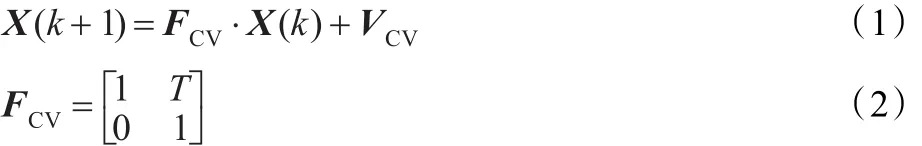
CA模型的一维离散状态方程为：

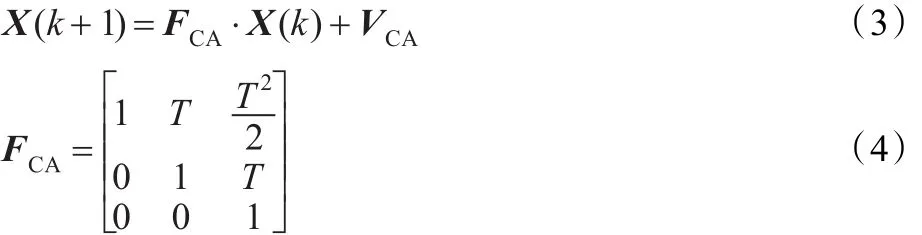
（2）自适应“当前”统计（ACS）模型

CS模型的一维离散状态方程为：

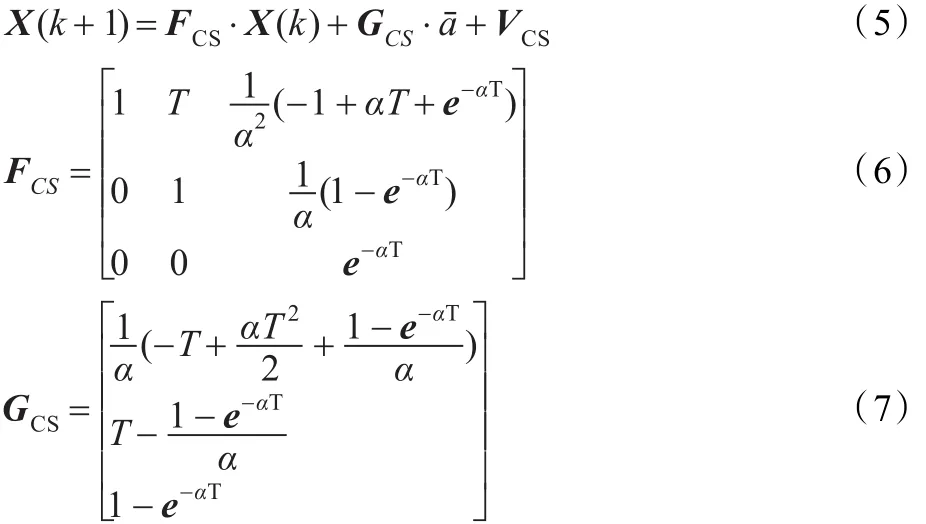
其中，a¯为当前加速度均值，α为机动时间常数的倒数（机动频率），过程噪声VCS是均值为零，方差为QCS的高斯白噪声，且

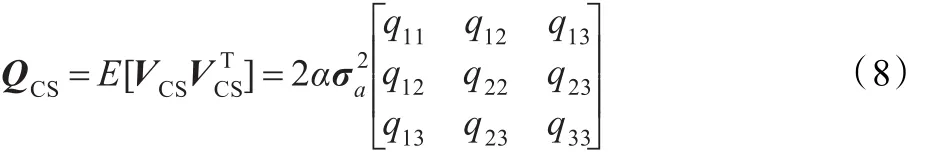
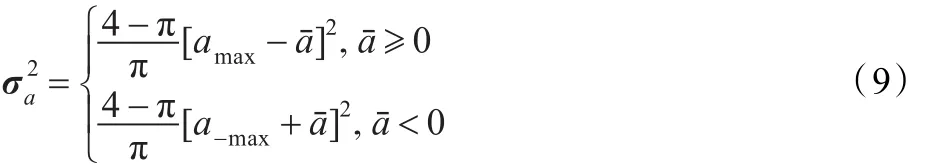
式中，amax和a-max分别为最大正负加速度。

从上式可以看出amax和a-max对机动加速度方差有直接影响，而会影响过程噪声的方差QCS，从而影响滤波器的跟踪精度[4]。而且由于目标的运动状态是时刻变化的，不论amax和a-max取值较小、较大或是取定值均不能完全适应目标的整个运动过程，可见amax和a-max对于目标的跟踪精度的影响还是较大的。参考文献[5]提出了一种ACS模型，通过采用IMM算法中的模型概率uj(k)调节amax和a-max，从而达到调节当前加速度的方差σ2a的目的，使ACS模型能够更加适应目标的运动状态。

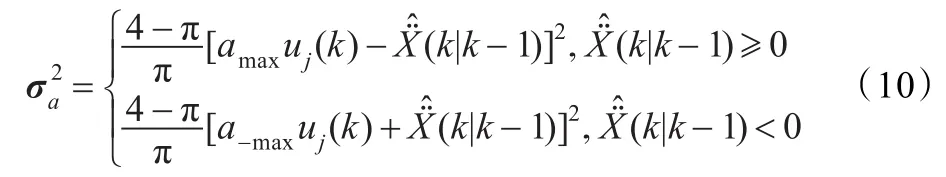
3 基于强跟踪滤波器的交互式多模型算法

IMM算法是一种基于软切换的机动目标跟踪方法。它对于目标的不同运动状态，采用不同的模型滤波器。各模型滤波器通过状态估计的组合实现相互作用，模型之间的转换通过一个马尔可夫链进行。最后的组合状态估计是由各模型滤波器估计的加权和得到的[6-8]。现将具有N个模型的IMM算法从k-1时刻到k时刻的递推分以下5步[1]：

（1）状态估计的交互式作用

设从模型i转移到模型 j的转移概率为Ptij：

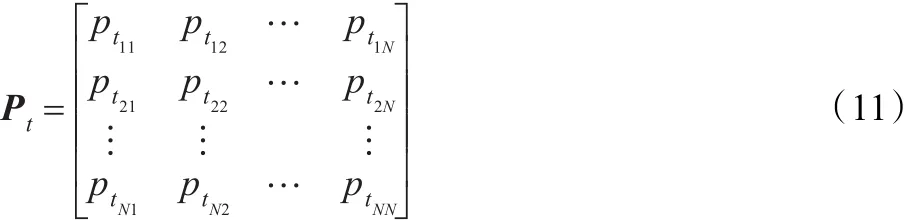
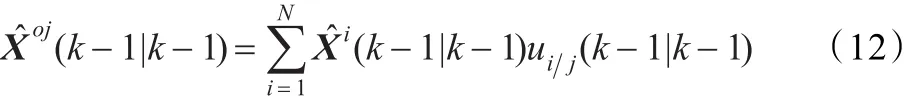
其中：

（2）模型修正

（3）模型可能性计算

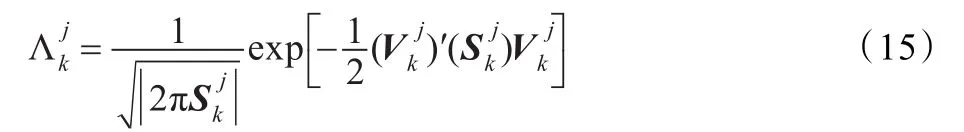
其中：

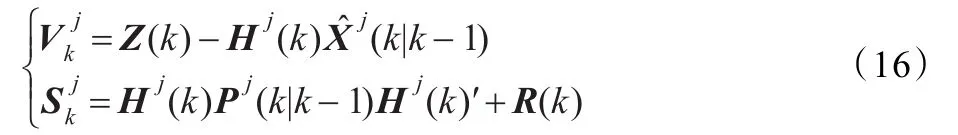
（4）模型概率更新

模型 j的概率更新如下：

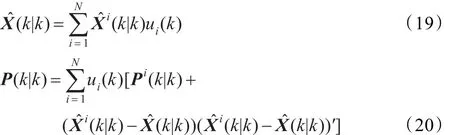
目前IMM算法大多采用EKF对机动目标进行跟踪，但是EKF具有鲁棒性较差、预测误差协方差P(k|k-1)和增益矩阵K(k)不能随残差改变等缺点[9]。针对上述缺点，周东华提出了一种强跟踪滤波器（STF）[10]，该滤波器采用在线选择适当的增益K(k)，使得均方误差最小，输出的残差近似为高斯白噪声。因此当目标状态发生突变时，强跟踪滤波器仍能较好地保持对目标实际状态跟踪。本文借鉴强跟踪滤波器的思想，引入时变的渐消因子，提出一种基于强跟踪滤波器的交互式多模型（STF-IMM）算法。该算法可以根据目标运动情况实时调整增益，提高跟踪性能。

STF-IMM算法如下：

首先由CV、CA和ACS模型组成模型集，然后采用下面的STF算法进行滤波处理：

（1）新息（残差）方程

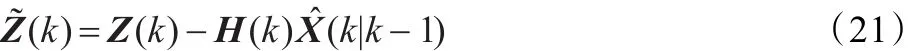
（2）滤波估值方程

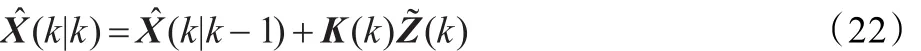
（3）预测估值方程

（4）滤波增益方程

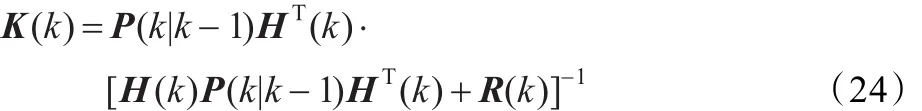
（5）滤波估值协方差

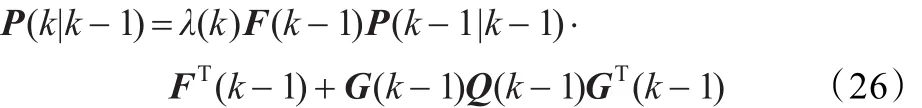
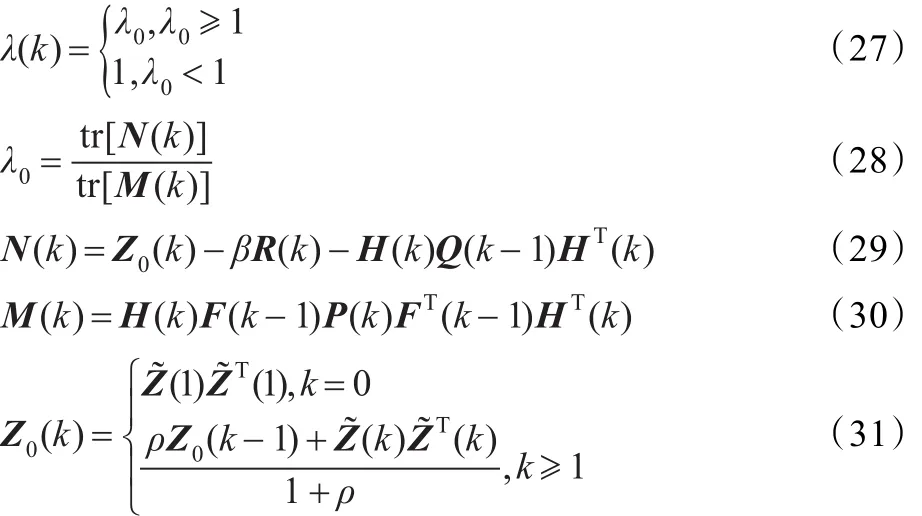
（6）预测估值协方差渐消因子由下式计算[11]： 0＜ρ≤1为遗忘因子，一般取ρ=0.95，β≥1为弱化因子，一般取经验值，Z˜(1)为初始残差。

可以看出，在跟踪一般机动目标时，速度预测值X˙^(k|k-1)和速度估计值 X˙^(k|k)相差不大，故渐消因子λ(k)较小，上述强跟踪卡尔曼滤波算法也就退化为经典卡尔曼滤波算法。当目标运动状态发生突变时，速度估计值X˙^(k|k)要偏离速度预测值X˙^(k|k-1)，强跟踪滤波器根据残差的增大而增大渐消因子，使得λ(k)≥1，自适应地调节增益，迫使残差近似正交，从而提高状态突变时的跟踪性能。

同时，STF-IMM算法与EKF-IMM算法相比，主要是增加了渐进因子的计算。通过分析可知，渐进因子的时间复杂度为T(n)=O(n3)。与整个算法相比，该时间复杂度是非常小的，而STF-IMM算法提高了系统的跟踪性能，说明STF-IMM算法具有较强的实用性。

4 仿真结果

为了检验算法的有效性，本文模拟了一组双目标的运动场景：目标1做加速机动，目标2做“几字”机动。两个目标的运动态势如图1所示。

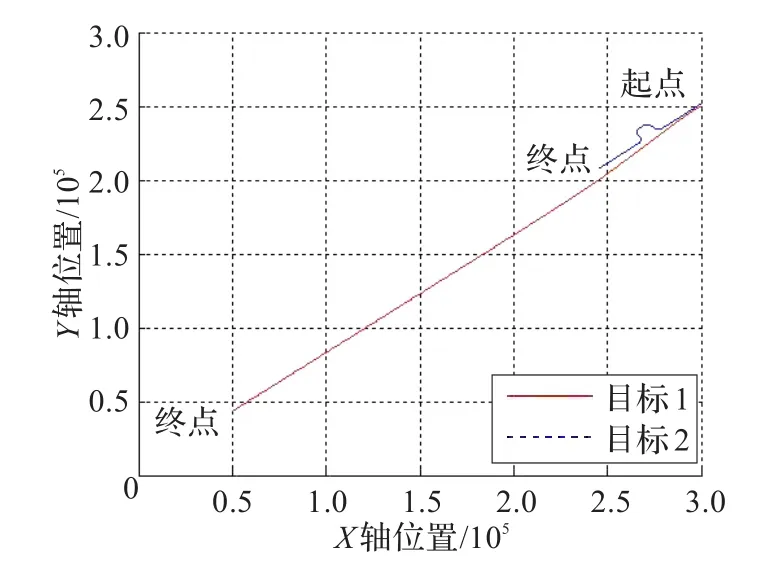
图1 目标运动态势图

考虑两个目标做高度不变的平面运动，z=3 000 m。目标1的初始位置和初始速度分别为[300 km，250 km]和[－80 m/s，－50 m/s]。目标1在0～50 s，100～150 s和200～250 s做匀速运动，在50～100 s做加速度为[－1 Gm/s，－1 Gm/s]的匀加速度运动，在150～200 s做加速度为[－4 Gm/s，－3 Gm/s]的匀加速度运动。目标2的初始位置和初始速度分别为[300 km，252 km]和[－250 m/s，－200 m/s]。目标2在0～85 s 和165～250 s做匀速运动，在85～165 s做角速率约为5.67（°）/s的“几字”机动。两个目标的运动轨迹如图2所示。

本文采用Monte Carlo仿真实验比较STF-IMM和EKF-IMM算法，二者均采用CV、CA和ACS模型组成模型集。两种算法中模型的转移概率矩阵为采样间隔为T=0.25 s；测距误差σr=200 m，测角误差σθ= 3°，测速误差σv=3 m/s；Monte Carlo仿真次数是500次。

图2 目标运动轨迹图

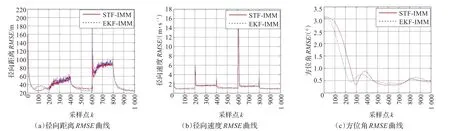
图3 目标1仿真结果

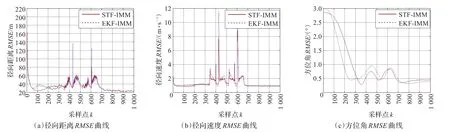
图4 目标2仿真结果

表1 两种算法的平均RMSE比较

为使仿真结果可比，本文采用均方根误差作为实验结果的评价指标，RMSE定义为：

式中，N为Monte Carlo仿真的次数，i表示第i次仿真，X(k|k)和 X^i(k|k-1)表示第i次仿真时k时刻目标状态的真值及总体预测值，考核的目标状态在为目标的径向距离、径向速度和方位角。STF-IMM与EKF-IMM算法统计的RMSE曲线如图3和图4所示，图中，红色实线为STF-IMM算法的RMSE曲线，蓝色虚线为EKF-IMM算法的RMSE曲线。表1是统计出的两种算法在非机动段和机动段的平均RMSE。

仿真结果显示，STF-IMM与EKF-IMM算法在非机动段的径向距离、径向速度和方位角的估计误差各有优劣，这表明目标在非机动段时，两种算法的跟踪性能基本相同。主要是由于目标在非机动段做匀速运动，目标的速度预测值和估计值相差不大，强跟踪滤波器也就退化为卡尔曼滤波器。而在机动段，STF-IMM算法的估计误差在径向速度和方位角上均小于EKF-IMM算法，径向速度和方位角比径向距离更能反映算法的跟踪性能，这说明在跟踪机动目标方面，STF-IMM算法的跟踪性能要略优一些。从图中可以看到STF-IMM的滤波器能够比较快速地收敛，并且在多处目标运动状态发生变化的时刻，两种算法的径向速度状态估计误差都出现了局部峰值，这是由于此时目标的运动状态正在发生变化，且本文引入了STF渐消因子λ(k)，因此在目标运动状态发生变化的时刻，STF-IMM算法的估计误差较小，说明本文提出的方法也能更好地适应目标运动状态的突变。

5 结论

本文研究了一种基于强跟踪滤波器的交互式多模型算法，通过在滤波器中引入STF渐消因子，根据残差动态地调整增益矩阵，增强了目标在发生强机动和突发机动时的跟踪能力。仿真实验表明，STF-IMM算法可以有效地提高系统对机动目标的跟踪性能，特别是在目标运动状态发生突变时，跟踪效果要优于EKF-IMM算法。

[1]何友，修建娟，张晶炜，等.雷达数据处理及应用[M].2版.北京：电子工业出版社，2012-06.

[2]范小军，刘锋.一种新的机动目标跟踪的多模型算法[J].电子与信息学报，2007，29（3）：532-535.

[3]周东华，叶银忠.现代故障诊断与容错控制[M].北京：清华大学出版社，2000.

[4]张永胜，嵇成新.一种基于当前统计模型的模糊交互多模型算法[J].火力与指挥控制，2003，28（1）：51-55.

[5]刘建书，李人厚，刘云龙.基于“当前”统计模型的交互式多模型算法[J].系统工程与电子技术，2008，30（7）：1351-1354.

[6]Mazor E，Dayan J，Bar-Shalom Y.Interacting multiple model in target Tracking[J].IEEE Trans on Aerospace and Electronics，1998，34（1）：103-123.

[7]Paeipour E，Bar-Shalom Y.IMM tracking of maneuvering target in the presence of Glint[J].IEEE Trans on Aerospace and Electronics，1998，34（4）：996-1003.

[8]Li R X，Bar-shalom Y.Perfomance Prediction of the interacting multiplie model algorithm[J].IEEE Trans on Aerospace and Electronics，1993，31（4）：755-771.

[9]范小军，刘锋，秦勇，等.基于STF的“当前”统计模型及自适应跟踪算法[J].电子学报，2006，34（6）：981-984.

[10]周东华.时变时延的在线自适应估计[J].电子学报，1999，27 （12）：61-63.

[11]徐毓，金以慧，杨瑞娟.基于强跟踪滤波器的多目标跟踪方法[J].传感器技术，2002，21（3）：17-20.

ZHANG Ying,HE Fengshou,ZHENG Shiyou

中航工业雷达与电子设备研究院 航空电子系统射频综合仿真航空科技重点实验室，江苏 无锡 214063

Aviation Key Laboratory of Science and Technology on AISSS,Radar and Avionics Institute ofAVIC,Wuxi,Jiangsu 214063,China

Aiming at the problem of the robustness of EKF-IMM is below average,an interacting multiple models algorithm using Strong Tracking Filter（STF）is proposed.Through introducing a fading factor of strong tracking filter,this algorithm realizes the realtime adjusting the gain of the filters,and updating the adaptive tracking performance and tracking precision for maneuvering targets accordingly.The Monte Carlo simulation result shows that this algorithm has the same tracking effect for nonmaneuvering target as EKF-IMM,and the tracking performance for maneuvering target is superior to EKF-IMM on radial velocity and azimuth.The simulation results verify that this algorithm has better performance than EKF-IMM in tracking maneuvering targets. Key words：maneuvering target tracking;Interacting Mutiple Model（IMM）;Strong Tracking Filter（STF）;fading factor;ACS model

A

TN953

10.3778/j.issn.1002-8331.1108-0053

ZHANG Ying,HE Fengshou,ZHENG Shiyou.Interacting multiple models algorithm using strong tracking filter.Computer Engineering and Applications,2013,49（7）：132-135.

张莹（1985—），女，助理工程师，研究领域：目标跟踪；贺丰收（1979—），男，工程师，研究领域：目标跟踪；郑世友（1972—），男，博士，高级工程师，研究领域：目标跟踪，资源管理。E-mail：ruifengzhang1985@163.com

2011-08-04

2011-09-30

1002-8331（2013）07-0132-04

CNKI出版日期：2011-12-09 http://www.cnki.net/kcms/detail/11.2127.TP.20111209.1002.070.html