基于新维无偏灰色马尔可夫的交通事故预测

赵 玲，许宏科

ZHAO Ling1，2,XU Hongke1

1.长安大学 电子与控制工程学院，西安 710064

2.西安邮电大学 通信与信息工程学院，西安 710121

基于新维无偏灰色马尔可夫的交通事故预测

赵 玲1，2，许宏科1

ZHAO Ling1，2,XU Hongke1

1.长安大学 电子与控制工程学院，西安 710064

2.西安邮电大学 通信与信息工程学院，西安 710121

交通事故预测是交通安全评价、规划和决策的基础。在传统灰色预测模型和马尔可夫链理论的基础上，利用新信息优先的思想，建立了等维新息无偏灰色马尔可夫预测模型。该模型通过结合灰色预测与马尔可夫链理论的特点，用无偏灰色预测模型拟合系统的发展变化趋势，并以此为基础进行马尔可夫预测，在每一步预测中不断推陈出新，更新原始数据。以2001年—2010年全国道路交通事故死亡人数实测值作为原始数据，构建预测模型，预测其2011年—2015年事故死亡人数。结果表明：等维新息无偏灰色马尔可夫预测模型的误差更小，精度更高，尤其适合中长期预测。

交通安全；交通事故预测；新维无偏灰色马尔可夫模型；马尔可夫链；等维新息

1 引言

道路交通安全是一个复杂的系统，受到人、车、路、环境等多种因素的综合影响[1]。目前用于交通事故预测的方法主要有回归分析法、时间序列法、SVM法、神经网络法、灰色预测法等[2-5]。大部分方法普遍存在着“长周期、大区域、低信度”的缺陷，它需要大量的历史数据，然后进行数学分析，得出相对稳定的发展趋势，但它没有充分考虑到实际的长期发展趋势是波动的。而灰色系统理论主要研究“小样本、贫信息”的不确定系统，在交通事故预测中得到了广泛的应用。

灰色预测是灰色系统理论的重要组成部分，其中应用较为广泛的是文献[6-7]提出的传统GM（1，1）模型，它主要适用于预测时间短，数据资料少，波动不大的系统对象，只需很少的几个数据即可建立模型进行预测。但由于传统GM（1，1）模型本身的缺陷[8]，使其仅能适用于短期预测和原始数据序列按指数规律变化且变化速度不是很快的场合。无偏灰色预测模型[9]消除了传统灰色预测模型本身所固有的偏差，其实只是一种无偏的指数模型，模型准确度优于传统GM（1，1）模型。但无论是哪一种GM（1，1）模型，其预测的几何图形都是一条较为平滑的曲线，对随机波动性大的数据序列进行预测时，预测值起伏不定，影响预测准确度。

马尔可夫预测适用于随机波动性较大的问题的预测[10]，由于道路交通系统是一个动态的时变系统，道路交通事故作为道路交通系统这一灰色系统的行为特征量，它的发生呈现某种变化趋势的非平稳随机过程。所以可以利用灰色预测和马尔可夫预测各自特点建立道路交通事故的灰色马尔可夫预测模型，文献[11-12]提出的灰色马尔可夫预测模型用GM（1，1）模型拟合系统的发展变化趋势，并以此为基础进行马尔可夫预测，这样既可以互补两者优势，又克服了两者的不足。与一般灰色GM（1，1）预测模型相比，预测的相对误差虽然明显降低了，但仍存在越往后预测准确度越低的问题，即它只对短期预测具有较高的准确度。

为解决随机波动性大的动态过程的中长期预测问题，本文建立一种新维无偏灰色马尔可夫预测模型[13]。以无偏GM（1，1）模型拟合得到的系统发展变化趋势为基础进行马尔可夫预测，同时利用新信息优先的思想，用灰色马尔可夫预测的最新预测结果不断更新建模用的原始数据，应用于道路交通事故衡量指标的预测，不但保留了短期预测准确度高的优点，而且对于中长期预测准确度也有提高。

2 无偏灰色预测模型的建立

文献[9]研究了传统灰色预测模型的特性，证明了传统灰色预测模型是有偏差的指数模型，并在此基础上提出了无偏灰色预测模型。具体模型建立过程如下：

设原始序列X(0)={x(0)(1),x(0)(2),…,x(0)(n)}，其中x(0)(k)≥0，k=1，2，…，n。

（1）作 X(0)的一阶累加得到生成序列 X(1)={x(1)(1)，

（2）确定数据矩阵B和Yn：

（3）用最小二乘法计算一阶线性微分方程的待估参数a和u：

（4）计算无偏GM（1，1）模型的参数b和A。对呈现指数变化趋势的原始数据序列 x(0)(k)=Aeb(k-1),k=1,2,…,n，作一次

按传统GM（1，1）方法建模可得：

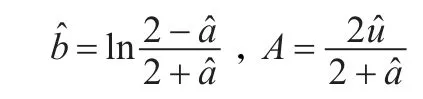
无偏GM（1，1）模型不仅不存在传统GM（1，1）模型所固有的偏差，消除了传统GM（1，1）模型在原始数据序列增长率较大时失效的现象，而且无需进行累减还原，简化了建模步骤，提高了模型的计算速度。

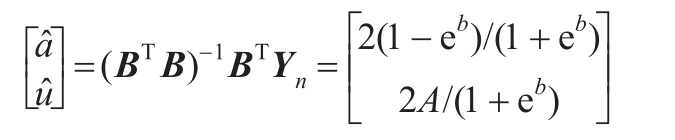
由此求得用传统GM（1，1）模型参数a^、u^表示的b和A的估计为：

3 对无偏灰色预测模型进行马尔可夫链改进

3.1 状态划分

设原始序列的无偏灰色预测值为 y^(k)，以 y^(k)= x^(0)(k+1)=Aebk曲线为中心将系统划分为与 y^(k)曲线平行的m个条形区域，任一状态区间⊗i表达为：⊗i=[⊗i1，⊗i2]，其中：⊗i1=y^(k)+Ai，⊗i2=y^(k)+Bi，Ai、Bi是平移常数（m、Ai、B均依据对象和原始数据而定）。

3.2 计算状态转移概率矩阵

设 Nij(n)为由状态⊗i经过n步转移到状态⊗j的原始数据样本数；Ni为处于状态⊗i的原始数据样本数，称Pij(n)=Nij(n)/Ni为由状态⊗i到状态⊗j的n步状态转移概率。则构造n步状态转移概率矩阵为：

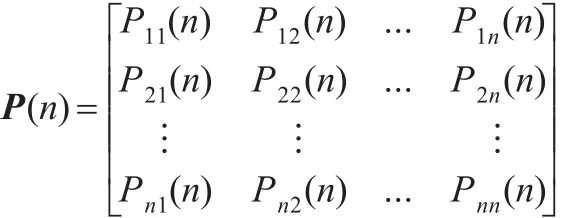
状态转移概率矩阵P(n)反映了系统各状态之间的转移规律。通过状态转移概率矩阵和初始状态，就可以确定未来的发展趋势。通过考察一阶状态转移矩阵P(1)即可确定预测对象的下一步转移状态。当矩阵P(1)中某行有2个或2个以上相同或相近时，可以参考P(2)或P(m)来确定状态的未来转向。

3.3 确定预测值

未来的转移状态⊗i确定之后，也就确定了预测值的变动区间[⊗i1，⊗i2]，取该区间的中点，则可得 x^(k+1)=(⊗i1+⊗i2)/2为数据x(k+1)的无偏灰色马尔可夫预测方法的预测值。

4 新维无偏灰色马尔可夫预测模型

在任何一个灰色系统的发展过程中，随着时间的推移，将会不断地有一些随机扰动或驱动因素进入系统，使系统的发展相继受其影响。无偏灰色马尔可夫预测模型也是一样，准确度较高的仅仅是原点数据以后的1～2个数据。越向未来发展，即越是远离时间原点，模型的预测准确度越低。考虑到这些模型都是建立在对历史数据的分析统计之上，只有在历史数据较为准确可靠的情况下，预测准确度才会较高。因此，在实际应用中，必须不断地考虑那些随着时间推移相继进入系统的扰动因素，淡化历史数据，随时将进入系统的新信息置入 X(0)中，建立等维新息模型，进而提高中长期预测的准确度。

新维无偏灰色预测模型是一种对传统灰色马尔可夫预测模型的改进。先用无偏灰色马尔可夫模型预测一个值，将其补充到已知数据之后，同时去掉最老的一个数据，保持数列等维，再建立无偏灰色马尔可夫模型预测下一个值，将其结果补充到数列之后，去掉最老的一个数据，这样进行下去，直到完成预测目标或达到预测精度为止。

新维无偏灰色马尔可夫预测模型的构建步骤为：

（1）原始数据序列 X(0)={x(0)(1)，x(0)(2)，…，x(0)(n)}；

（2）对X(0)作一次累加生成模块X(1)；

（3）确定数据矩阵B、Yn，求参数α和u：

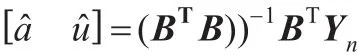
（5）设第k期无偏灰色马尔可夫预测为y^(k)，令y^(k)= x^(0)(k+1)=Aebk，以y^(k)为中心将系统划分为m个状态；

（6）计算一步状态转移概率矩阵(Mij)m×m；

（10）返回步骤（2），重复步骤（2）到步骤（9），直到计算完成需预测数据的预测值为止。

5 实例分析

根据我国2001年—2010年的全国道路交通事故死亡人数数据，利用本文的新维无偏灰色马尔可夫模型进行交通事故的拟合与预测分析。首先选取2001年—2010年全国道路死亡人数，共10个数据作为原始样本（见表1，表中数据摘自2011年《中国交通年鉴》公安部交通管理局道路交通事故统计）。

5.1 建立死亡人数的无偏灰色模型

根据无偏灰色建模的方法，结合Matlab编程环境，将表1的原始数据序列输入到编写程序中，求得b=-0.068 383 77，A=121 713.1，建立无偏灰色的数据模型，y^(k)=x^(0)(k+1)= Aebk=121 713.1e-0.068 383 77k，预测结果见表2。该模型的平均残差相对值为ε¯=3.46%，平均精度为p=96.54%。

5.2 建立死亡人数的无偏灰色马尔可夫模型

在无偏灰色模型预测的宏观变化趋势基础上进行马尔可夫预测，根据样本数据的实际情况，将序列划分成如下4个状态，其中x¯(0)(k)为建模数据的平均值。

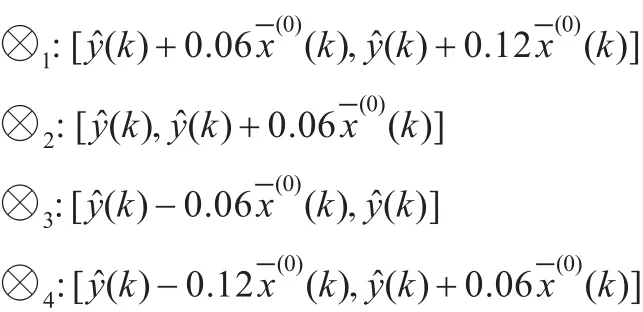
由于原始数据序列的最后一个数的状态转向不确定，所以，去除2010年交通事故次数数据，通过分析可知落入各状态的样本数分别为n1=2，n2=2，n3=4，n4=1，然后得一步转移概率矩阵为：

由于2001年道路交通事故死亡人数处于状态⊗4，结合一步转移概率矩阵P(1)，可推测2002年全国道路交通死亡人数最可能处于状态⊗3，因而其最可能的预测值为：y(0)(1)=x^(0)(1)-0.03x¯(0)(k)=113 668-0.03×90 307=110 959; 2010年交通事故死亡人数最可能处于状态⊗3，因而其最可能的预测值为：y(0)(9)=x^(0)(9)-0.03x¯(0)(k)=65 773-0.03× 90 307=63 064。同理，可预测2011年—2015年交通事故的死亡人数。无偏灰色马尔可夫模型的预测结果见表2，该模型的平均残差相对值为 ε¯=2.47%，平均精度为p=97.53%。

5.3 建立死亡人数的新维无偏灰色马尔可夫模型

对原始序列进行等维新息处理，去掉2001年的数据，加入利用无偏灰色马尔可夫预测模型所得的2011年预测值（即58 717），即以2002年—2011年的事故死亡人数作为新的数据序列如上预测2012年的事故死亡人数，建立的无偏灰色预测模型为：y^(k)=x^(0)(k+1)=Aebk=118 867.9e-0.077 118 62k，该模型的平均残差相对值为 ε¯=2.18%，平均精度为p=97.82%。用新维无偏灰色马尔可夫模型预测的2012年交通事故死亡人数为：y(0)(10)=x^(0)(10)-0.02x¯(0)(k)=57 366-0.02×85 586=55 654。

表1 2001年—2010年我国道路交通事故死亡人数统计

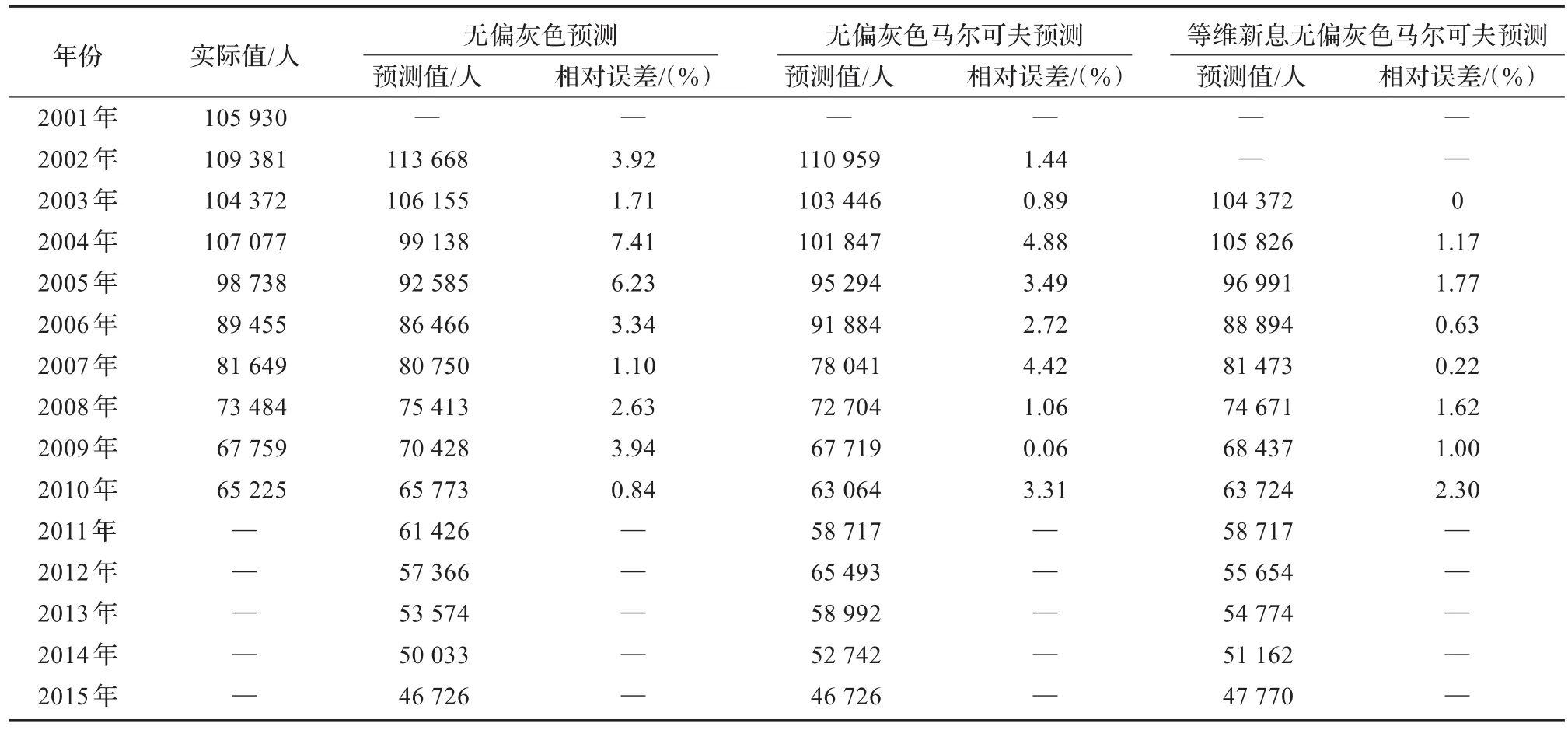
表2 2001年—2010年全国道路交通事故死亡人数的实际值和各种方法的预测值

由于进行一次等维新息处理后，模型的平均残差相对值仍大于2%，所以继续进行等维新息处理，去掉2002年的数据，加入2012年的预测值（即55 654）。用2003年—2012年数据预测2013年数据时，建立的无偏灰色模型为y^(k)=x^(0)(k+1)=Aebk=114 905.1e-0.085 206 67k，该模型的平均残差相对值为ε¯=1.24%，平均精度为p=98.76%。用新维无偏灰色马尔可夫模型预测的2013年交通事故死亡人数为：y(0)(10)=x^(0)(10)+0.015x¯(0)(k)=53 574+0.015×79 974= 54 774。同理，可预测2014年交通事故死亡人数为：y(0)(10)= x^(0)(10)+0.015x¯(0)(k)=50 033+0.015×75 253=51 162；2015年交通事故死亡人数为：y(0)(10)=x^(0)(10)+0.015x¯(0)(k)=46 726+ 0.015×69 624=47 770。将本次等维新息灰色马尔可夫模型的拟合值及对未来5年的预测值列出，见表2。

5.4 模型比较

根据前述实例中各种模型拟合结果及预测结果的比较分析，可知新维无偏灰色马尔可夫模型预测出的全国道路交通死亡人数与无偏灰色模型和无偏灰色马尔可夫模型的结果相比（见表3），相对误差最小，拟合程度最高，可以用于道路交通死亡人数的预测，尤其在中长期预测中更具优势。

表3 预测模型的性能比较 （%）

6 结论

交通事故预测是交通安全评价、规划和决策的基础。本文研究思路避开了自然环境、社会经济条件和政策导向等因素，采用以灰色系统理论和马尔可夫链方法相结合的新维无偏灰色马尔可夫预测模型，对中长期的全国道路交通事故死亡人数进行预测，同时对原始数据进行等维新息处理，提高了中长期的预测精度，具体优越性体现在如下的几个方面：

（1）该模型是建立在传统灰色模型的基础之上，因此继承了灰色模型所需历史数据少的优点，避免了其他方法中“长周期、大区域、低信度”的缺陷，可以比较充分地利用有限的数据。

（2）无偏灰色预测模型不存在传统灰色预测模型固有的偏差。该模型可以根据历史数据的变化趋势进行预测，其应用范围较传统灰色预测模型有了很大扩展，不仅适用于指数型的数据，也适用于非指数型的数据，比较符合交通事故指标的实际变化趋势。

（3）利用等维新息思想对历史数据进行及时地更新与补充，建立新维无偏灰色马尔可夫模型，使得该模型更适合于交通事故指标的中长期预测，克服了一般灰色马尔可夫模型仅适用于短期预测的缺陷。

[1]刘强，陆化普，张永波，等.我国道路交通事故特征分析与对策研究[J].中国安全科学学报，2006，16（6）：124-128.

[2]邵辉，王钰，李保安，等.交通事故损失的时间序列分析[J].中国安全科学学报，2007，17（7）：10-13.

[3]Kalyoncuoglu S F，Tigdemir M.An alternative approach for modeling and simulation of traffic data：using artificial neural networks[J].Simulation Modeling Practice and Theory，2004，12（5）：351-362.

[4]Yang Z.Highway traffic accident prediction based on SVR trained by genetic algorithm[C]//Proceedings of the International Conference on Materials Science and Information Technology （MSIT），2012：5886-5889.

[5]韩文涛，张倩，贾安民.基于灰色系统的道路交通事故预测模型研究[J].西安建筑科技大学学报，2005，37（3）：375-377.

[6]邓聚龙.灰色预测与决策[M].武汉：华中理工大学出版社，1988.

[7]刘思峰，谢乃明.灰色系统理论及其应用[M].北京：科学出版社，2008.

[8]熊岗，陈章潮.灰色预测模型的缺陷及改进方法[J].系统工程，1992，10（6）：32-36.

[9]吉培荣，黄巍松，胡翔勇.无偏灰色预测模型[J].系统工程与电子技术，2000，22（6）：6-7.

[10]陈克龙.随机过程及其应用[M].南京：东南大学出版社，1993. [11]钱卫东，刘志强.基于灰色马尔可夫的道路交通事故预测[J].中国安全科学学报，2008，18（3）：33-36.

[12]李相勇，张南，蒋葛夫.道路交通事故灰色马尔可夫预测模型[J].公路交通科技，2003，20（4）：98-100.

[13]李东，苏小红，马双全.基于新维灰色马尔科夫预测模型的股价预测算法[J].哈尔滨工业大学学报，2003，35（2）：244-248.

1.School of Electronic and Control Engineering,Chang'an University,Xi'an 710064,China

2.School of Communication and Information Engineering,Xi'an University of Posts and Telecommunications,Xi'an 710121,China

The prediction of traffic accident is the basis of transportation safety,assessment and decision-making.Based on the traditional grey forecasting model and Markov chain theory,as well as the new information has priorities,equal dimension and new information unbiased grey Markov forecasting model is established.Combining the characteristics of grey prediction and Markov theory,the model imitates the development tendency of the forecast system with unbiased grey model,while Markov prediction is used to forecast the fluctuation along the tendency.The newest data are gradually added while the oldest one is removed from original data sequence.Then,the number of road traffic deaths from 2000 to 2010 is taken as original data to establish forecasting model predicting the deaths from 2011 to 2015.Experimental results show that the prediction accuracy of the equal dimensional and new information grey Markov forecasting model has fewer errors and better forecasting precision, especially for medium and long-term prediction.

transportation security;traffic accident prediction;new dimensional unbiased grey Markov model;Markov chain; equal dimension and new information

A

U492.3

10.3778/j.issn.1002-8331.1209-0176

ZHAO Ling,XU Hongke.Traffic accident prediction based on equal dimension and new information unbiased grey Markov model.Computer Engineering and Applications,2013,49（7）：35-38.

国家自然科学基金（No.60804049）；陕西省教育厅自然科学基金（No.11JK0897）。

赵玲（1977—），女，博士生，讲师，研究方向为交通事故预测，交通安全与控制；许宏科（1963—），男，博士，教授，博士生导师，研究方向为交通控制，现代交通信息系统。E-mail：zhaoling9543@163.com

2012-09-18

2012-11-19

1002-8331（2013）07-0035-04

CNKI出版日期：2012-12-05 http://www.cnki.net/kcms/detail/11.2127.TP.20121205.1652.006.html