遥感图像配准的稳健投影非负矩阵分解方法

段西发，田 铮，齐培艳，贺飞跃

DUAN Xifa1，2,TIAN Zheng1,QI Peiyan1，2,HE Feiyue1

1.西北工业大学 应用数学系，西安 710129

2.太原科技大学 应用数学系，太原 030024

遥感图像配准的稳健投影非负矩阵分解方法

段西发1，2，田 铮1，齐培艳1，2，贺飞跃1

DUAN Xifa1，2,TIAN Zheng1,QI Peiyan1，2,HE Feiyue1

1.西北工业大学 应用数学系，西安 710129

2.太原科技大学 应用数学系，太原 030024

由于要配准的目标存在可能的形变，震前和震后遥感图像的配准变得很困难。为了解决这个问题，提出基于稳健的投影非负矩阵分解（RPNMF）的配准方法来精确的配准形变目标。给出一种稳健的投影非负矩阵分解方法来获得震前震后形变目标的共同投影空间，利用在共同投影空间的投影来配准形变目标。为验证该算法的有效性，做了两个实验：2008年5月12日汶川地震前后的SAR图像的配准；唐家山堰塞湖的变化检测。与现有方法进行比较，结果表明该方法能够有效地得到形变目标的共同投影空间，并取得了很好的配准结果；同时，堰塞湖的变化检测也得到了很好的结果。

遥感图像；形变目标；非负矩阵分解；稳健的投影非负矩阵分解；投影空间；异常值

1 引言

图像配准（image registration）就是将不同时间、不同传感器或不同视角获取的两幅或多幅图像进行匹配、叠加的过程[1]。现有的图像配准方法主要分为两大类：基于区域的和基于特征的配准方法[2]。基于区域的方法不需要检测图像显著的特征，其主要采用优化的方法[3-4]。这些方法依赖于图像的灰度分布，因此有其内在局限性。基于特征的方法利用从两幅图像中提取的显著特征进行匹配，从而达到配准的目的。由于其不直接利用图像灰度信息，当要配准的图像发生灰度改变或几何变化时仍能取得好的配准结果。因而基于特征的方法被广泛应用于遥感图像配准中[5-6]。

基于特征的配准方法包含五个步骤：预处理、特征提取、特征匹配、变换函数、重采样。其中，特征提取、特征匹配和变换函数需要很多操作技巧，这里面最困难的就是特征匹配[7]。如果有些特征匹配是不正确的，则会导致变换函数的错误，最终会导致完全错误的配准结果，因此需要一个稳健有效的匹配方法。近年来，图谱方法被广泛用于特征匹配[8-11]，Scott和Higgins[8]根据从待配准图像里提出的特征点集，构造了两个特征点集之间的亲近矩阵，并对亲近矩阵进行奇异值分解（Singular Value Decomposition，SVD），然后根据亲近矩阵的奇异值和奇异向量来确定特征之间的匹配关系。SVD方法当图像间的旋转或尺度过大时失效。为了解决这个问题，Shapiro和Brady[9]分别对两个特征点集构造特征点集内部的亲近矩阵，通过对亲近矩阵进行特征分解，以亲近矩阵的特征向量为列向量构造模式矩阵，最后通过比较两个特征点集模式矩阵的行向量来确定特征之间的匹配关系。Shapiro和Brady的方法没利用特征值并要求两个特征点集之间的个数相等。为了克服这些问题，Caelli[10]提出了一种特征空间投影聚类的方法。该方法只用到亲近矩阵的k个最大的特征值和与之对应的特征向量，并对特征向量按照对应的特征值进行了规范化，通过点集在投影空间的位置来确定相似性，最后通过聚类的方法来确定特征的匹配关系。Wang和Hancock[11]用核主成分分析（KPCA）的方法来确定特征的匹配关系并讨论了Shapiro和Brady的方法与KPCA之间的关系：从KPCA的观点来看，图谱方法中用来建立亲近矩阵的相似函数等价于KPCA中的核函数。图谱方法是一种矩阵分解方法，通过矩阵分解将特征点集映射到一个线性或非线性的共同空间，然后在该空间确定特征的匹配关系。

图谱方法的一个缺点是通过谱分解产生的基矩阵不能反映特征矩阵的非负性。为了克服这个问题，Lee和Seung引进了非负矩阵分解（NMF）[12-13]，NMF在机器学习、信号处理、模式识别[14-16]等领域已经成为一个很重要的工具。目前，NMF已得到很大发展，并提出了很多NMF的改进方法。为得到稀疏解，文献[17]将稀疏性约束加入NMF；文献[18]把鉴别信息作为罚项加入到目标函数中，以达到最大化类间距离，最小化类内距离，构造了判别NMF；为研究低维流形的局部结构，文献[19]提出了局部保持的NMF，它通过在点和点的邻域加入约束实现；文献[20]提出了投影NMF（PNMF）。PNMF通过一个投影子空间来近似数据矩阵，和NMF相比，PNMF考虑更少的参数但能产生更稀疏的分解矩阵，这在特征提取和聚类中是非常需要的。

本文要解决的是震前震后SAR（Synthetic Aperture Radar）图像中的形变目标配准问题。虽然图谱方法能有效地刻画目标的结构，但其有两个缺点：一是不能反映数据矩阵的非负性；二是对目标的结构变化很敏感。表现在配准上就是当目标没有形变时配准效果可能很好，但如果目标发生较小的形变其配准结果可能马上变得很差。NMF能反映数据矩阵的非负性，且数据的整体结构信息由组成整体的局部结构构成，其用于配准有直观的解释。然而，它和图谱方法有一样的缺点，就是对结构变化很敏感。这是因为其损失函数是L2的，这在统计学上是不稳健的，会因为异常值的存在影响到最后得到的分解基矩阵，从而影响最后的配准结果。针对这个问题，本文提出基于稳健的投影非负矩阵分解（RPNMF）的形变目标配准方法，通过RPNMF来剔除异常值的影响，从而得到形变目标的共同投影空间，以实现形变目标的精确配准。

2 非负矩阵分解和投影非负矩阵分解

NMF是在矩阵元素均为非负的情形下对矩阵进行的一种非负分解算法。给定数据集 X=[x1,x2,…,xn]∈RD×n，X的每一列都是一个样本数据。NMF就是找到一个D×K的非负矩阵W=[wik]∈RD×K和一个 K×n的非负矩阵H=[hjk]∈RK×n，使得X≈WH。其中W是基矩阵，它的列向量张成一个子空间，H是系数矩阵。为了找到合适的W和H，使得X≈WH，首先需要定义损失函数。Lee和Seung在文献[12]中给出了两个损失函数，第一个是基于Frobenius范数的损失函数：

第二个是基于改进的Kullback-Leibler散度的损失函数：

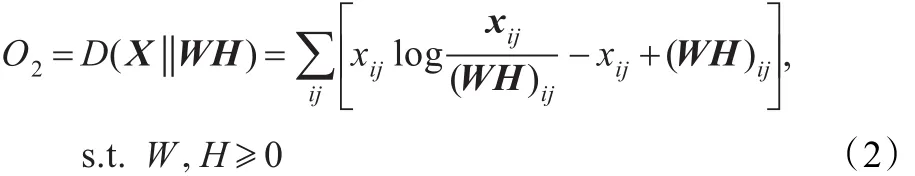
针对这两个损失函数，Lee和Seung给出了两种乘性迭代公式。最小化目标函数O1的迭代算法为：

最小化目标函数O2的迭代算法为：

Lee和Seung在文献[13]中，给出了迭代算法（3）和（4）对目标函数（1）和（2）的收敛性证明。

实际应用中，要求K≪D，K≪n。因此，NMF的实质是：在加性描述的限制下，在尽可能保持信息完整的情况下，将高维的随机模式简化为低维的随机模式，这种简化的基础是估计出数据中的本质结构。从代数的观点看，X≈WH，W的列是基，H依W的存在而存在。每一个数据向量xi可以表示为基W 的线性组合xi≈WHi，其中xi和Hi为X和H的第i列。

PNMF是对NMF的一个改进，它定义为下面的优化问题：

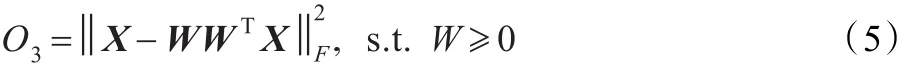
Yang给出如下的更新规则[20]：

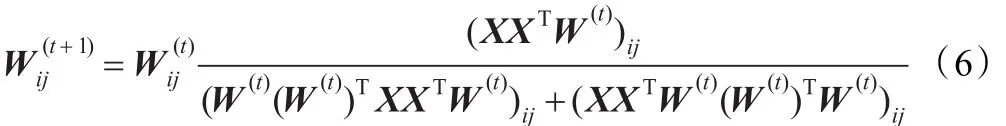
和NMF相比，PNMF考虑更少的参数，却能产生更稀疏的矩阵，这正是在特征提取和聚类中所需要的。但不管是NMF还是PNMF，它们的损失函数都是L2的，由稳健统计学[21]可知，这是不稳健的，其分解基矩阵容易受少数异常值的影响而产生较大变化。为了保持PNMF的优点同时得到稳健的分解基矩阵，给出下面的稳健投影非负矩阵分解（RPNMF）。

3 稳健的投影非负矩阵分解（RPNMF）

为了消除异常值的影响而得到稳健的投影非负矩阵分解，给出如下的目标函数：

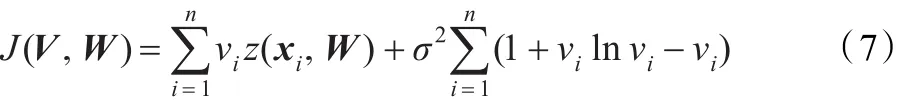
3.1 迭代公式

为了迭代公式求解的方便，将目标函数（7）转化如下：

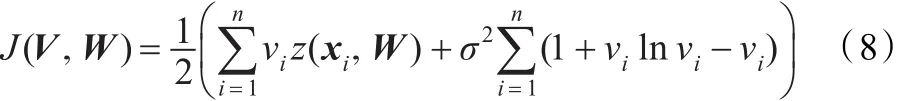
首先求解V，将式（8）对vi求偏导并令其为0可得：

由式（9）可得：

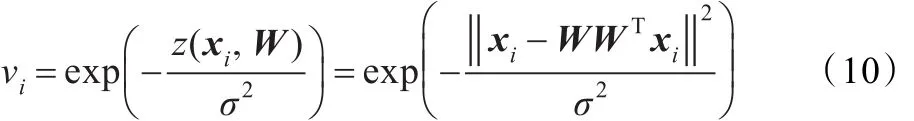
下面来求解W，对目标函数（8）进行如下转换：

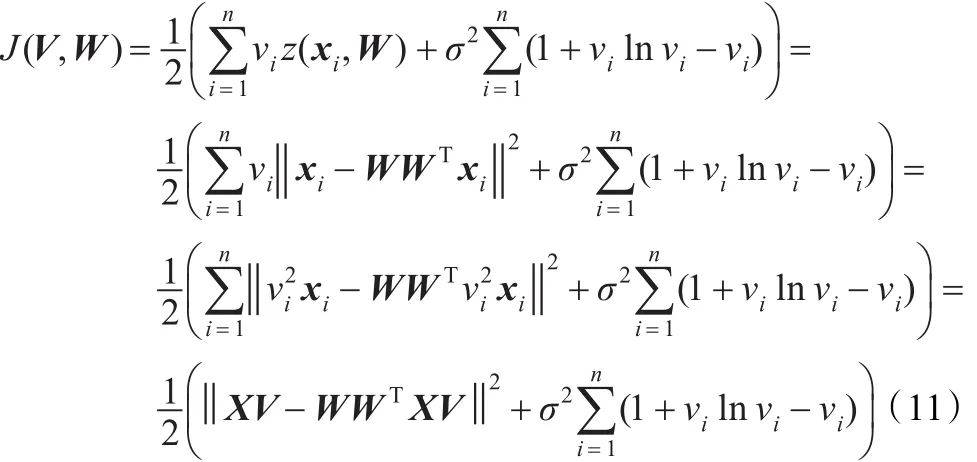
本节采用梯度下降法求解上述目标函数。由于负梯度方向是目标函数值减少最快的方向，沿着负梯度方向计算可以最快达到极小点。为此，首先求得目标函数（11）关于W的偏导数为：

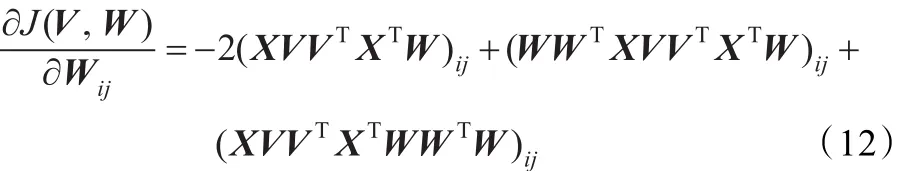
建立加性迭代准则：

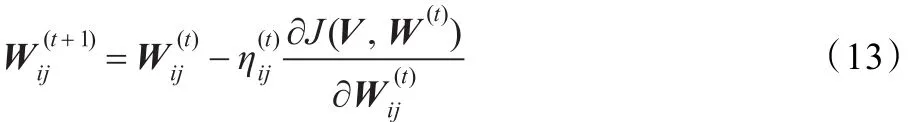
将式（12）和式（14）代入式（13），可得乘性迭代格式如下：

3.2 收敛性分析

定义1[15]如果 G(u，u′)≥F(u)，当且仅当 u=u′时有G(u，u)=F(u)，则称G(u，u′)为F(u)的辅助函数。

引理1[15]如果G(u，u′)是F(u)的辅助函数，则利用更新准则：

更新u可使F(u)单调不增。其中u(t)和u(t+1)分别为u的当前值和更新后的值。

证明

为了证明目标函数（11）在迭代公式（15）下的收敛性，将目标函数（11）改写为：

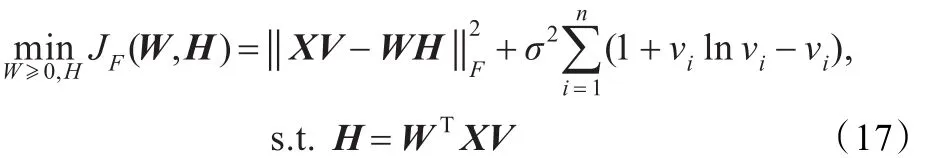
改写后的目标函数（17）对应的Lagrange函数为：

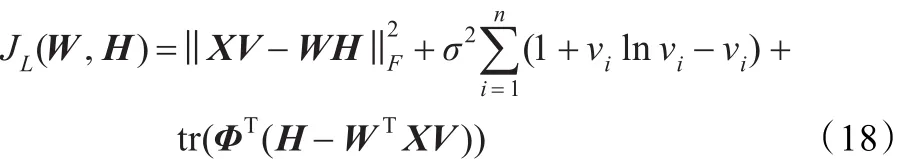
其中Φ=[φij]为Lagrange乘数。

引理2函数

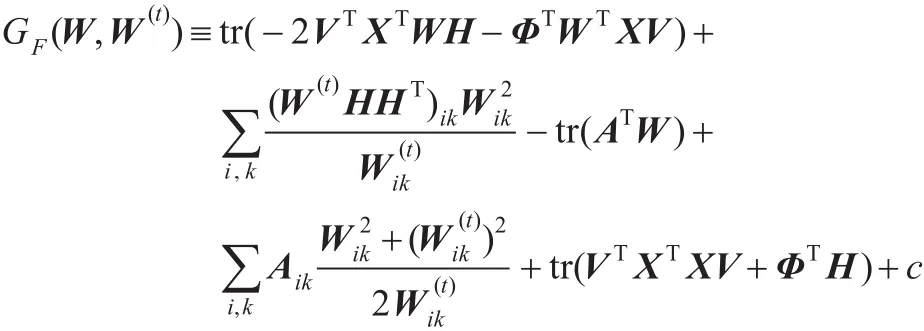
是Lagrange函数JL(W，H)的辅助函数，其中

证明 GF(W，W)=JL(W，H)非常明显，因此只需证明GF(W，W(t))≥JL(W，H)。

因为：

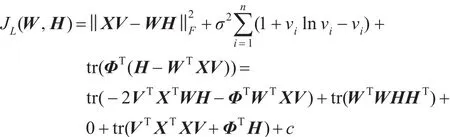
而且有：

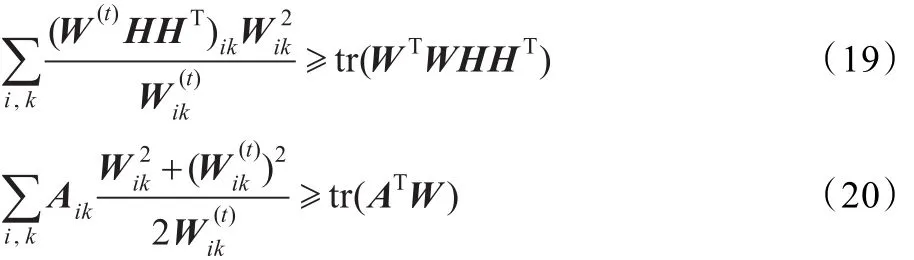
式（19）、（20）的证明参见文献[20]。

因此有GF(W,W(t))≥JL(W,H)，即GF(W,W(t))为JL(W,H)的辅助函数。

定理1（收敛性定理）目标函数（8）在迭代公式（15）下是单调不增的。

证明 因为：

函数GF(W，W(t))的极值可以通过到，即

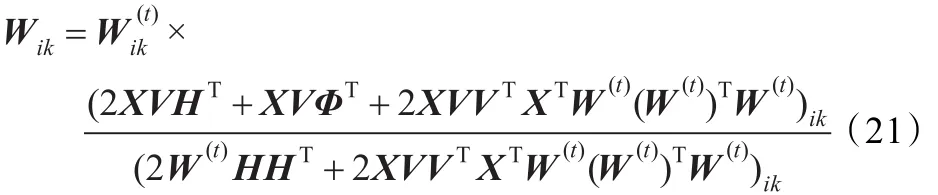
Lagrange乘子可以通过Karush-Kuhn-Tucker（KKT）条件求得：

将式（24）和H=(W(t))TXV代入（21），即得迭代公式（15）。

因此目标函数（8）在迭代公式（15）下是单调不增的。又因为目标函数（8）是非负的，有下界零，因此目标函数在迭代公式（15）下是收敛的。

3.3 RPNMF算法

对一个给定点集 X=[x1，x2，…，xn]∈ℝD×n，RNMF算法如下：

首先对vi(1≤i≤n)赋初值1

动力电池从汽车上报废后，部分电池具有梯级应用价值，如应用在通信电站、电网储能等领域。梯级应用结束后，报废的动力电池具有材料再生价值，即拆解回收有价金属材料。动力电池电极材料中含有Li、Ni、Co等有价值的金属，如表2所示，通过合理的技术回收利用，可实现经济效益。

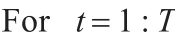
步骤1利用迭代公式（15）计算W。

步骤3利用式（10）求vi。若满足收敛条件或者达到最大迭代步数maxiter2，进行步骤4；否则返回步骤1。

End

步骤4对所有的vi(1≤i≤n)，如果vi≤η，则xi认为是异常值。

权vi反映了数据 xi的重要性程度，vi越大，xi越重要。η设定的稍大一点是可以接受的，因为在实际应用中，正常的样本数据要远多于异常值的数目，即使有一小部分正常样本数据被认为是异常值，而剔除也不会影响最后的结果精度。通过剔除对分解基影响很大的异常值，本文提出的RPNMF方法能保证点集X和Y具有近似相同的分解基矩阵WX和WY。

4 基于共同投影空间上投影的配准

在上一章，得到了形变目标近似相同的分解基矩阵。假定由RPNMF方法得到的点集X和Y的分解基矩阵为：

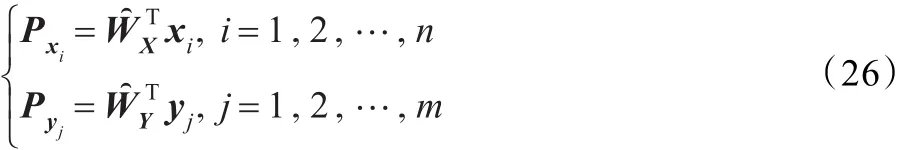
由式（26）可计算判别矩阵D如下：

若Dij为所在行和所在列的最小值，则认为xi和 yj是匹配的。因为Dij为所在行和所在列的最小值，所以不会出现X中多个特征点匹配Y中一个特征点的情况，也不会出现X中一个特征点匹配Y中多个特征点的情况。这样通过判别矩阵D，就可以保证得到的X中特征点和Y中特征点的对应关系是一对一的。利用特征的匹配关系，可以很容易求得两个点集的变换函数。

5 实验

为验证本文算法的有效性，做了两个实验。第一个实验验证本文算法对形变程度不同的形变目标配准的稳健性；第二个实验，将本文算法应用到变化检测中。

5.1 曾家湾水库和秦家碾水库的配准

在这一部分，分别对形变程度不同的两个形变目标进行了配准，使用的是5.12汶川地震前后曾家湾和秦家碾水库的ALOS-PALSAR图像。震前图像拍摄于2008年2月17日，震后图像拍摄于2008年5月19日。因为本文研究的是形变目标配准，首先使用加权核图割[22]对图像进行分割以获得形变目标，然后使用曲率尺度空间角点检测子[23]来提取形变目标的特征点，最后，分别用SVD、Shapiro和Brady的方法、PNMF以及本文提出的RPNMF方法来对特征点进行匹配。基于特征点的匹配关系，通过最小二乘法来确定震前震后图像变换函数（实验中的变换函数采用的是射影变换函数Projective Transformation）的参数。最后，对四种方法的匹配效果和配准效果进行了比较分析。

图1给出了曾家湾水库的原始的ALOS-PALSAR图像和它对应的分割后图像。

图1 原始的曾家湾水库的ALOS-PALSAR图像和它对应的分割后图像

为验证本文RPNMF方法的有效性，分别研究图像的匹配效果和配准效果。图2给出了曾家湾水库的匹配结果和配准结果，其中图（a）、（c）、（e）和（g）分别是SVD、Shapiro 和Brady方法、PNMF、RPNMF方法的匹配结果，图（b）、（d）、（f）和（h）是相应的配准结果。从匹配结果来看，SVD方法的效果最差，其误匹配较多，且有严重匹配错误的误匹配，Shapiro和Brady方法以及PNMF方法效果较好，其误匹配比SVD方法要少，且基本上没有匹配错误严重的误匹配，本文所提的RPNMF方法的匹配效果最好，其基本上没有误匹配。为了对匹配结果做一个定量分析，分别给出了四种方法的总匹配数（N）、正确匹配数（NC）及正确匹配率（Correct Correspondence Rate，CCR），其中正确匹配率定义如下：

图2 曾家湾水库的匹配结果和配准结果

从表1可以看出，提出的RPNMF的正确匹配率最高，达到了91%，而SVD、Shapiro和Brady方法以及PNMF的正确匹配率分别为62%、69%和72%，且本文方法RPNMF的正确匹配个数也比其他方法要高。

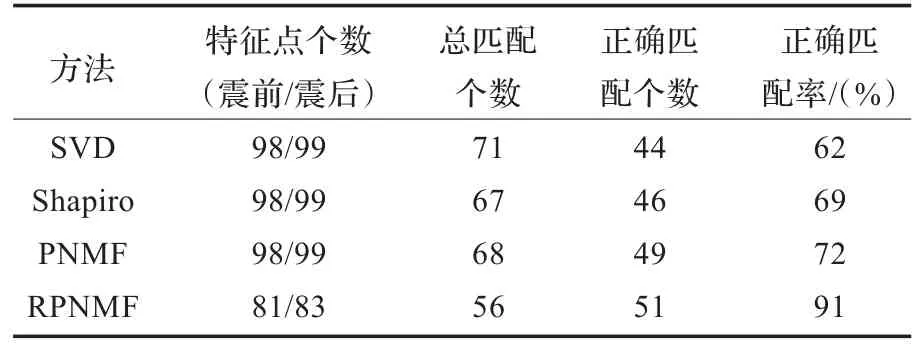
表1 匹配结果

下面来分析RPNMF的配准效果。从图2可以看出，RPNMF的配准效果最好，Shapiro和Brady的方法以及PNMF方法效果次之，SVD方法效果较差。同样，为了对配准效果给出一个定量分析，引入均方根误差（Root Mean Square Error，RMSE）作为配准效果的衡量标准。表2给出了配准结果的均方根误差。从表2可以看出，RPNMF的RMSE最小，配准效果最好；Shapiro和Brady的方法以及PNMF方法的RMSE较大；SVD方法的RMSE最大。

表2 配准的RMSE 像素

为验证本文方法对形变程度不同的形变目标配准的有效性，对形变程度较小的秦家碾水库进行了配准实验。

图3给出了秦家碾水库的原始的ALOS-PALSAR图像和它对应的分割后图像。

图3 原始的秦家碾水库的ALOS-PALSAR图像和它对应的分割后图像

图4给出了匹配结果和配准结果。其中图（a）、（c）、（e）和（g）分别是SVD、Shapiro和Brady方法、PNMF以及RPNMF的匹配结果，图4（b）、（d）、（f）和（h）是相应的配准结果。为了对配准结果有一个更直观的认识，在图4中给出的是震前震后形变目标的配准结果。从图4可以看出，RPNMF的匹配效果和配准效果最好，其他三种方法的匹配效果和配准效果也比较好，与Shapiro和Brady方法以及PNMF方法相比，SVD方法的匹配效果和配准效果稍差一些。

表3给出了匹配结果的总匹配数、正确匹配数和正确匹配率。从表3可以看出，虽然本文的RPNMF方法的匹配个数和正确匹配个数相比其他方法要少了一些，但正确匹配率仍然是最高的。Shapiro和Brady方法及PNMF方法的正确匹配率也很高，分别达到了88%和86%，SVD的正确匹配率稍低一点，达到了75%。

表4给出了配准结果的RMSE，从中可以看出，RPNMF配准的RMSE仍然是最小的。

从上面两个形变目标的配准可以看出，本文的RPNMF方法对形变程度不同的形变目标都取得了好的配准结果。而其他三种矩阵分解方法，当形变目标的形变程度较小时，也取得了较好的匹配结果和配准结果；但当形变目标形变程度较大时，它们的匹配效果和配准效果会变得较差。本文的RPNMF方法实现了对形变目标的稳健配准。

图4 秦家碾水库的匹配结果和配准结果

表3 匹配结果

表4 配准的RMSE 像素

5.2 唐家山堰塞湖的变化检测

唐家山堰塞湖（东经104°26'17''，北纬31°50'51''）位于涧河上游距北川县城约6 km处的唐家山山谷，是北川灾区面积最大、危险最大的一个堰塞湖。图5（a）和图5（c）分别为ALOS AVINIR-2在不同时刻获得的图像，其中（a）为2007年3月31日获得的震前图像，（c）为2008年5月16日获得的震后图像。为进行变化检测，使用加权核图割方法[23]对震前震后图像进行分割，以获得水体目标。图5（b）和图5（d）分别给出了从震前和震后图像中提取的水体目标。

图5 唐家山地区的ALOS AVNIR-2图像（（a）和（c）都为Band 1、Band 2、Band 3的合成图像）

为检测水域变化情况，将（b）和（d）进行配准，并计算了特征点集的RMSE，SVD、Shapiro和Brady方法、PNMF以及RPNMF的RMSE分别为23.48、14.16、13.52、3.35，配准结果见图6。

图6 唐家山堰塞湖配准结果

图6中黑色的表示震前震后没有发生变化的区域，蓝色的表示震后新增的水域。图6（d）表明唐家山堰塞湖的张坪区域水域宽度从震前的92 m变为震后的563 m，发生了很大改变。

最后，从时间复杂度来说，假设两个特征点集中特征点的个数分别为m和n，则SVD方法的时间复杂度为O(min(mn2，m2n))；Shapiro和Brady方法的时间复杂度为O(max(m3，n3))；PNMF的时间复杂度为O(nTDK)，其中，D为数据的维数，K为特征空间的维数，T为迭代次数；RPNMF的时间复杂度为O(nT1T2DK)，T1、T2分别为内迭代和外迭代的次数。在上面实验中，D=2，K=5；T=1 100， T1=100，T2=800，能达到10-5的精度要求。因此，四种算法的时间复杂度相当，只是相差一个常数。

6 结论

本文提出基于RPNMF的配准方法来精确配准震前震后SAR图像中的形变目标。通过实验可以看到，RPNMF方法取得了比其他三种矩阵分解方法更好的配准结果。SVD、Shapiro和Brady方法以及PNMF三种矩阵分解方法由于目标函数的不稳健而使得它们得到的震前震后形变目标的投影空间相差较大，这导致其对结构变化敏感而不适合形变目标的配准。本文的主要贡献：首先，提出RPNMF来获得震前震后形变目标的共同投影空间，然后给出了基于共同投影空间的形变目标配准方法。实验结果表明，和其他矩阵分解方法相比，本文方法匹配精度更高，配准结果更准确。

[1]Brown L G.A survey of image registration techniques[J]. ACM Computing Surveys，1992，24（4）：326-376.

[2]Zitová B，Flusser J.Image registration methods：a survey[J]. Image Vision Computing，2003，21（11）：977-1000.

[3]Ye F，Su L，Li S.Automatic multi-resolution image registration based on genetic algorithm and Hausdorff distance[J].Chin Opt Lett，2006，4（7）：386-388.

[4]Aguilar W，Frauel Y，Escolano F，et al.A robust graph transformation matching fornon-rigid registration[J].Image and Vision Computing，2009，27：897-910.

[5]Bentoutou Y，Taleb N，Kpalma K，et al.An automatic image registration for applications in remote sensing[J].IEEE Trans on Geoscience and Remote Sensing，2005，43（9）：2127-2137. [6]Liu X Z，Tian Z，Ding M T.A novel adaptive weights proximity matrix for image registration based on R-SIFT[J].Int J Electron Commun，2011，65（12）：1040-1049.

[7]Dawn S，Saxena V，Sharma B.Remote sensing image registration techniques：asurvey[C]//ProcISISP，Trois-Rivières，QC，Canda，Jun 30-Jul 2，2010，6134：103-112.

[8]Scott G L，Longuet-Higgins H C.An algorithm for associating the feature of two images[J].Proceedings of the Royal Society of London：Series B Biological Sciences，1991，244：21-26.

[9]Shapiro L S，Brady J M.Feature-based correspondence：an eigenvector approach[J].Image and Vision Computing，1992，10（5）：283-288.

[10]Caelli T.An eigenspace projection clustering method for inexactgraphmatching[J].IEEE TransonPAMI，2004，26 （4）：515-519.

[11]Wang H F，Hancock E R.A kernel view of spectral point pattern matching[J].Proceedings of Structural，Syntactic，and Statistical Pattern Recognition，2004，3138：361-369.

[12]Lee D D，Seung H S.Learning the parts of objects by nonnegative matrix factorization[J].Nature，1999，401：788-791.

[13]Lee D D，Seung H S.Algorithm for NMF[J].Advances in Neural Information Processing Systems，2001，13（2）：556-562.

[14]Brunet J P.Metagenes and molecular pattern discovery using matrix factorization[J].Proc Natl Acad Sci，2004，101（12）：4164-4169.

[15]Shastri B J，Levine M D.Face recognition using localized features based on non-negative sparse coding[J].Mach Vis Appl，2007，18（2）：107-122.

[16]Wang Y.Fisher non-negative matrix factorization for learning local features[J].Int J Pattern Recogn Artif Intell，2005，19 （4）：495-511.

[17]Kim J，Park H.Sparse nonnegative matrix factorization for clustering，in CSE TechnicalReports[R].Georgia Institute of Technologhy，2008：1-15.

[18]Zafeiriou S，Tefas A，Buciu I，et al.Exploiting discriminant information in non-negative matrix factorization with application to frontal face verification[J].IEEE Transactions on Neural Networks，2007，17（3）：683-695.

[19]Gu Q，Zhou J.Neighborhood preserving nonnegative matrix factorization[C]//Proceedingsof the 20th British Machine Vision Conference，2009.

[20]Yang Z，Oja E.Linear and nonlinear projective nonnegative matrix factorization[J].IEEE Transactionson NeuralNetworks，2010，21（5）：734-749.

[21]Huber P J.Robust statistics[M].[S.l.]：Wiley-Interscience，1981.

[22]Salah M B，Mitiche A，Ayed I B.Multiregion image segmentation by parametric kernel graph cuts[J].IEEE Trans on Image Process，2011，20（2）：545-557.

[23]He X C，Yung N H C.Curvature scale space corner detector with adaptive threshold and dynamic region of support[C]// Proceedings of ICPR'04，2004，2：791-794.

1.Departments of Applied Mathematics,Northwestern Polytechnical University,Xi'an 710129,China

2.Departments of Applied Mathematics,Taiyuan University of Science and Technology,Taiyuan 030024,China

For pre-and post-earthquake remote-sensing images,registration is a challenging task due to the possible deformations of the objects to be registered.To overcome this problem,a registration method based on robust projective Nonnegative Matrix Factorization is proposed to precisely register the variform objects.Firstly,a Robust Projective Nonnegative Matrix Factorization（RPNMF）method is developed to capture the common projection space of the variform objects.Secondly,a registration approach is derived from the common projection space of the variform objects.Finally,two experiments are conducted to verify the effectiveness of the proposed method：one is the SAR image registration in Wenchuan earthquake on May 12,2008,the other is change detection of Tangjiashan barrier lake.The results show that the method is very effective in capturing the common projection space of variform objects and generalizes well for registration.Meanwhile,good performance on the change detection of barrier lake is obtained.

remote-sensing image；variform object;Nonnegative Matrix Factorization（NMF）;Robust Projective Nonnegative Matrix Factorization（RPNMF）;projection space;outliers

A

TP751.1；TN911.73

10.3778/j.issn.1002-8331.1207-0276

DUAN Xifa,TIAN Zheng,QI Peiyan,et al.Registration of remote-sensing images using robust projective nonnegative matrix factorization.Computer Engineering and Applications,2013,49（7）：28-34.

国家自然科学基金（No.60972150，No.10926197）;西北工业大学基础研究基金（NO.JC20110277）。

段西发（1979—），男，博士研究生，主要研究方向为遥感图像配准及分类；田铮（1948—），女，教授，博士生导师，主要研究方向为图像处理与模式识别；齐培艳（1979—），女，博士研究生，主要研究方向为非线性时间序列分析；贺飞跃（1974—），男，博士研究生，主要研究方向为SAR图像分割及配准。E-mail:xfduan@163.com

2012-07-24

2012-12-04

1002-8331（2013）07-0028-07

CNKI出版日期：2012-12-26 http://www.cnki.net/kcms/detail/11.2127.TP.20121226.1120.002.html