集值信息系统基于限制相容关系的属性约简

乔全喜，秦克云

QIAO Quanxi1，2,QIN Keyun1

1.西南交通大学 数学系，成都 610031

2.河南理工大学 数学与信息科学学院，河南 焦作 454000

集值信息系统基于限制相容关系的属性约简

乔全喜1，2，秦克云1

QIAO Quanxi1，2,QIN Keyun1

1.西南交通大学 数学系，成都 610031

2.河南理工大学 数学与信息科学学院，河南 焦作 454000

讨论集值信息系统基于限制相容关系的属性约简方法；给出相似水平核心属性的特征。通过实例说明该算法能够得到集值信息系统的相对约简。

粗糙集；集值信息系统；对称限制；相容关系；属性约简

1 引言

粗糙集理论是由波兰数学家Pawlak提出的处理不精确、不完全数据的有效工具[1-2]。它依据对象之间的不可分辨性将论域中的对象聚类成基本知识，利用基本知识，通过上、下近似运算来描述数据对象的不确定性，从而导出概念的分类或决策规则。目前，粗糙集理论已广泛应用于属性约简[3-9]、规则提取[10-11]、模式识别与分类[12-13]等人工智能领域。经典粗糙集模型对知识的表达是建立在完备信息系统中的属性所诱导的等价关系基础上的，但在实际应用中，由于问题的复杂性，通常人们得到的数据是不精确和不完善的。如果信息系统中某个对象的属性是未知的，则称这种信息系统为不完备信息系统；如果一些对象的某个属性值不是取一个值，也不是取空集，而是取几个值，这种信息系统称之为集值信息系统。近年来，一些学者针对集值信息系统的知识发现与属性约简做了许多研究工作。文献[3]基于相容关系TA讨论了集值信息系统的约简理论与方法，给出了该集值信息系统与其完备化信息系统的关系，提出了最大分布约简与最优完备化概念，得到了从集值信息系统获取决策规则的方法。2006年Guan等人[4]在文献[3]的基于相容关系TA确定的最大相容类在集值信息系统上，定义了两种类型的上、下粗糙近似算子，构造了相应的粗糙集模型，然后通过引入最大相容类的属性描述，给出了集值信息系统的规则提取与优化方法，并根据定义的粗糙集模型讨论了集值信息系统的三种类型的属性约简。宋笑雪等在文献[14-15]中借助集合包含关系在集值信息系统上定义了一种新的相容关系，并研究了集值决策表在两种不同关系TA与下的广义约简方法和最优广义决策规则的提取，给出了协调集值决策表的属性约简与不协调集值决策表的分配约简，并讨论了协调集值决策系统中不同类型的属性特征。Qian等人在文献[5]中比较详细地讨论了集值有序信息系统的优势粗糙集方法，对集值信息系统给出了更细致的刻画。文献[16]提出了描述子的概念，构建了一种新的粗糙集模型定义方法，并由协调描述子导出最优确定性决策规则，由非协调描述子导出了最优结合决策规则，讨论了描述子的相对约简以及一些不确定度量方法。文献[17]基于描述子概念讨论了不完备信息系统上可信决策规则的提取，并利用区分矩阵法给出了向上与向下描述子的相对约简，得到了不完备决策信息系统的最优可信决策规则。文献[18-19]基于限制相容关系和对称限制相容关系，分析比较了相应的粗糙集模型与已有粗糙集扩展模型之间的关系。文献[9]基于变精度相容关系对集值信息系统及集值决策表的约简理论与方法进行了比较深入、系统的研究。本文针对对称限制相容关系，研究集值信息系统以及集值决策表的属性约简的理论与方法，并给出了相应水平核心。

2 集值信息系统中的限制相容关系

设U是对象构成的非空有限集合，以下称为论域。按照Pawlak粗糙集理论，知识是对对象进行分类的能力。因此，U上的知识可以形式化地表示为U的划分，U上的知识库可以通过信息系统进行描述。

定义1[20]一个信息系统是一个三元组S=(U，A，F)，其中：

（1）U={x1，x2，…，xn}为对象集，每个 xi(1≤i≤n)称为一个对象；

（2）A={a1，a2，…，am}为属性集，每个aj(1≤j≤m)称为一个属性；

（3）F={fl|1≤l≤m}为对象属性值映射，其中fl:U→Vl，Vl是属性al的值域。

设S=(U，A，F)是信息系统。对于任意a∈A，由a可以确定论域U上的一个等价关系，称为由a确定不可区分关系，记为ind(a)，定义如下：

对于任意x，y∈U，(x，y)∈ind(a)当且仅当：fa(x)=fa(y)。

因此，信息系统本质上就是知识库，每一个属性决定一个知识。

集值信息系统是信息不确定与不完整的一种反映形式，具体可以定义如下：

定义2[20]称三元组S=(U，A，F)为集值信息系统，其中U={x1，x2，…，xn}为对象集，A={a1，a2，…，am}为属性集，F={fl|1≤l≤m}为对象属性值映射，其中 fl:U→P0(Vl)，Vl是属性al的值域，P0(Vl)表示Vl的所有非空子集构成的集合。若S=(U，A，F)是一个集值信息系统，d是论域U上一个决策属性，则称S=(U，A∪{d}，F)是一个集值决策表。

设S=(U，A，F)是一个集值信息系统，对任意a∈A，x∈U，fa(x)的值从语义方面主要有两种解释方式[4-5]：

（1）fa(x)的值被合取地解释。例如，设a表示属性“语言能力”，则 fa(x)={汉语，英语，法语}可以解释为对象x会说汉语、英语和法语；又如当按动物的“食性”将一群动物分类时，若以“0”表示“食草”，以“1”表示“食肉”，则可用无序数组{0，1}来表示“既食草又食肉”。

（2）fa(x)的值被析取地解释。例如，设a表示属性“语言能力”，则 fa(x)={汉语，英语，法语}也可以解释为对象x会说汉语、英语和法语中的一种语言。对于不完备信息系统，如果对象x在属性a下取空值并且空值存在，则 fa(x)可以表示取属性a的值域Va中的任何值，这时可以用a的所有可能取值Va作为 fa(x)的取值；如果已知 fa(x)必定不取某些值，比如不取b、c，则可用Va-{b，c}作为 fa(x)的取值。因此，不完备信息系统可以转化为析取解释的集值信息系统进行研究。

定义3[3]设(U，A，F)是集值信息系统，任意属性子集B⊆A，定义二元关系：

定义4[14]设(U，A，F)是集值信息系统，任意属性子集B⊆A，定义二元关系：

定义5[18]设(U，A，F)是集值信息系统，任意属性子集B⊆A，定义二元关系：

定义6[19]设(U，A，F)是集值信息系统，任意属性子集B⊆A，定义二元关系：

其中：

以上相容关系分别从不同的角度出发刻画了集值信息系统中对象之间的相似性，显然有：

接下来针对对称限制相容关系，研究集值信息系统以及集值决策表的属性约简理论与方法。

3 对称限制相容关系的属性约简

设S=(U，A，F)是集值信息系统，B⊆A，α∈(0，1]，令

定理1[19]设(U，A，F)是集值信息系统，RαB是如上定义的二元关系，则有：

（1）RαB是自反、对称二元关系；

下面讨论集值信息系统基于限制相容关系的属性约简方法，并给出相似水平核心属性的特征。

定义7设S=(U,A,F)是集值信息系统，B⊆A，α∈(0,1]，若，则称B是S的一个α分类协调集。若B是S 的 α分类协调集，且对于 B的任意真子集C⊂B，有，则称B是S的一个α分类约简。

集值信息系统S的α分类约简是保持所有对象的α相容类不变的极小属性子集。S的α分类约简是存在的，并且可能不唯一。S的所有α分类约简构成的集合记为redα(S)，而S的所有α分类约简的交集称为S的α分类核，记为coreα(S)，即coreα(S)=redα(S)。

根据定理1容易知道，B⊆A是集值信息系统S的α分类协调集等价于，或者等价于∀x∈U，。

定义8设S=(U，A，F)是一个集值信息系统，x，y∈U，为对象x与y的α区分属性集；并称

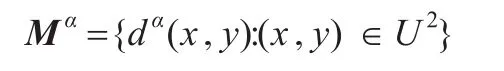
为集值信息系统S的α区分矩阵。

明显地，dα(x，y)≠∅当且仅当(x，y)∉RαA，并且对任意B⊆A，B∩dα(x，y)≠∅当且仅当(x，y)∉RαB。

根据定义8，对任意 x，y∈U及相似水平 α都有dα(x，x)=∅，dα(x，y)=dα(y，x)，即集值信息系统的α区分矩阵Mα是主对角线上元素全为∅的对称矩阵。

定理2设S=(U，A，F)是一个集值信息系统，B⊆A，α∈(0，1]是相似水平，则B是S的α分类协调集的充分必要条件是：其中：

充分性：假设∀dα(x，y)∈，B∩dα(x，y)≠∅。如果B不是 α分类协调集，那么必有，这表明存在(x，y)∈，但(x，y)∉.由(x，y)∉知 dα(x，y)≠∅，于是由假设就有 B∩dα(x，y)≠∅，从而(x，y)∉，这就与(x，y)∈矛盾。因此A是α分类协调集。

定理3设S=(U，A，F)是一个集值信息系统，α∈(0，1]是相似水平，则 c∈coreα(S)的充分必要条件是：存在dα(x，y)∈，使dα(x，y)={c}。

证明 必要性：设c∈coreα(S)，即c是S的一个α分类核心属性。记

容易看到∀dα(x，y)∈，都有 B∩dα(x，y)≠∅。于是由定理2知B是α分类协调集，从而存在C⊆B，使C是S的α分类约简，但明显地有c∉C，这就与c是α分类核心属性矛盾。因此必有dα(x，y)∈Mα(c)，使| dα(x，y)|=1，从而dα(x，y)={c}。

充分性：假设存在dα(x，y)∈，使dα(x，y)={c}。对于S的任意α分类约简B，由定理2知B∩dα(x，y)≠∅，从而有 c∈B，故有 c∈coreα(S)。对于集值信息系统(U，A，F)，若α，β∈(0，1]，α≤β，则有。从而对于任意x∈U，有。即随着相似水平的提高，集值信息系统的相容类或知识将会变得更细。另外，对于任意x，y∈U，显然有dα(x，y)⊆dβ(x，y)，即随着相似水平的提高，可以区分x、y的属性更多。

基于区分矩阵与区分函数，通过计算区分函数的极小析取范式可以找到完备信息系统的所有约简，这一方法也可以推广到集值信息系统。

是集值信息系统 S的 α区分函数，其中 ⋁dα(x，y)表示dα(x，y)中所有属性的析取。

定理4设S=(U，A，F)是一个集值信息系统，α∈(0，1]，B⊆A，则B是S的α分类约简的充分必要条件是：⋀A是α区分函数Δα(S)的极小析取范式中的一个合取子式。

例1考虑表1给出的集值信息系统。

表1 集值信息系统

取阈值α=0.5，经计算可得：

同理，对于任意x，y∈U，可求得d0.5(x，y)，构成区分矩阵如下：

于是，区分函数为：

从而S有唯一的0.5分类约简{a1，a2，a5}。

如果取阈值α=0.7，通过计算可得区分矩阵如下：

其中 X1={a1，a2，a4，a5}，X2={a1，a2，a3，a4，a5}，X3={a1，a2，a3，a5}。于是区分函数为：

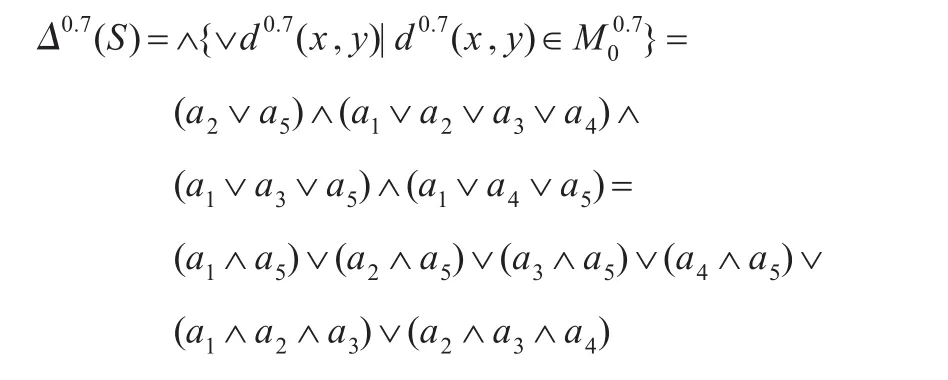
故有六个0.7分类约简：{a1，a5}，{a2，a5}，{a3，a5}，{a4，a5}，{a1，a2，a3}和{a2，a3，a4}。

4 结论

集值信息系统对象关于属性取集合值是信息不确定的一种反映形式。本文讨论了集值信息系统基于相对限制相容关系的属性约简方法，给出了相似核心属性的特征以及相对约简的计算方法。今后，将在本文的基础上，进一步讨论集值决策表基于相对限制相容关系的分配约简和正域约简方法。

[1]Pawlak Z.Rough sets[J].InternationalJournalofComputer and Information Science，1982，11：341-356.

[2]Pawlak Z.Rough sets：theoretical aspects of reasoning about data[M].Boston：Kluwer Academic Publishers，1991.

[3]Zhang W X，Mi J S.Incomplete information system and its optimal selections[J].Computers and Mathematics with Applications，2004，48：：691-698.

[4]Guan Y Y，Wang H K.Set-valued information systems[J]. Information Sciences，2006，176：2507-2525.

[5]Qian Y，Dang C，Liang J，et al.Set-valued ordered information systems[J].Information Sciences，2009，179：2809-2832.

[6]Li F，Yin Y Q.Approaches to knowledge reduction of covering decision systems based on information theory[J].Information Sciences，2009，179：1694-1704.

[7]洪晓蕾，王燕，莫执文，等.集值不完备信息系统上的一种知识约简方法[J].四川师范大学学报：自然科学版，2007，30（3）：266-269.

[8]陈子春，秦克云.集值信息系统在相容关系下的属性约简[J].模糊系统与数学，2009，23（1）：150-154.

[9]陈子春.集值信息系统的知识发现与属性约简研究[D].成都：西南交通大学，2011.

[10]Tsumoto S.Mining diagnostic rules from clinical databases using rough sets and medical diagnostic model[J].Information Sciences，2004，162：65-80.

[11]Tsai Y C，Cheng C H，Chang J R.Entropy-based fuzzy rough classification approach for extracting rules[J].Expert Systems with Application，2006，31（2）：436-443.

[12]Hu Q H，Yu D R，Xie Z X.Neighborhood classifiers[J].Expert Systems with Application，2008，34：866-876.

[13]Li Y，Shiu S C K，Pal S K.Combining feature reduction and case selection in building CBR classifiers[J].IEEE Transactions on Knowledge and Data Engineering，2006，18：415-429.

[14]宋笑雪，解争龙，张文修.集值决策信息系统的知识约简与规则提取[J].计算机科学，2007，34（4）：182-184.

[15]宋笑雪，张文修.基于集值决策属性的集值信息系统[J].计算机工程与应用，2007，43（17）：8-10.

[16]Leung Y，Wu W Z，Zhang W X.Knowledge acquisition in incomplete information systems：a rough set approach[J]. European Journal of Operational Research，2006，168（1）：164-180.

[17]Yang X，Xie J，Song X，et al.Credible rules in incomplete decision system based on descriptors[J].Knowledge-Based Systems，2009，22：8-17.

[18]吴鹏，杨勇，张阿红.基于集值的Rough集扩充模型[J].计算机工程与应用，2008，44（32）：134-136.

[19]鲍忠奎，杨善林.集值信息系统的粗糙集扩展模型[J].计算机工程与应用，2011，47（35）：22-24.

[20]张文修，梁怡，吴伟志.信息系统与知识发现[M].北京：科学出版社，2003.

1.Department of Mathematics,Southwest Jiaotong University,Chengdu 610031,China

2.School of Mathematics&Information Science,Henan Polytechnic University,Jiaozuo,Henan 454000,China

This paper is devoted to the discussion of attribute reduction of set-valued information system based on symmetry restriction tolerance relation.The characteristic of similar level core attribute is introduced.The example shows that this algorithm can obtain the relative reduction of set-valued information system.

rough set;set-valued information system;symmetry restriction;tolerance relation;attribute reduction

A

TP18；TP301

10.3778/j.issn.1002-8331.1209-0117

QIAO Quanxi,QIN Keyun.Attribute reduction of set-valued information system based on restriction tolerance relation. Computer Engineering and Applications,2013,49（7）：24-27.

国家自然科学基金（No.60875034）。

乔全喜（1964—），男，博士生，研究领域：粗糙集理论及其应用；秦克云（1962—），男，博士生导师，研究领域：代数逻辑与智能信息处理。E-mail：qiaoqx@hpu.edu.cn

2012-09-19

2012-12-03

1002-8331（2013）07-0024-04

CNKI出版日期：2012-12-24 http://www.cnki.net/kcms/detail/11.2127.TP.20121224.1515.005.html