基于协作中继的多元网络乘积码

淦明，李辉，戴旭初

(中国科学技术大学 电子工程与信息科学系，安徽 合肥 230027)

1 引言

在现代无线通信中，协作中继是通过采集和利用无线网络中离散分布的节点信息，节点终端间共享彼此之间的天线，形成虚拟MIMO系统，达到充分利用频谱、获得分集增益、实现信息分布式传输与处理的分集技术。由Ahlswede[1]引入的网络编码已被成功应用在中继节点上，如文献[2]提到在协作中继系统中通过充分利用多播传输中信息分组之间的相关性来获得容量的显著提高，然而基于XOR的网络编码稳健性较差，易错误传播并且难以推广到多用户场景。因此，近来许多研究工作[3～5]的重点转移到联合设计信道编码和网络编码，文献[5]提出了一种LDPC码和网络编码的联合编码，利用编码图匹配网络拓扑结构图，从而获得高分集增益，大幅度地提高了误码率性能。

为了加强错误纠错性能并同时能支持多个用户，文献[6～10]提出一种网络乘积编码协作方案，把分布式乘积码应用到协作中继中，它们分别使用汉明码、BCH码和LDPC码作为子码，通过相互独立的路径转发乘积码的不同部分到目的端。另外，文献[11]提出了中继端转发乘积码的校验软信息到目的端。然而，这些在目的端构建的全局乘积码的权重分布远达不到高斯分布。如文献[12～14]指出，一种码长很长的码字若它权重分布趋近于高斯分布，则该码字具有良好的误码率性能，文献[15]也证实了一种码长很长且码率较高的扩展单奇偶校验乘积码能获得接近香农极限的误码率性能。因此，本文基于协作中继场景设计了一种多元网络乘积码。该方法通过在中继上使用Turbo技术，并且对接收到的译码后源信息比特进行高码率编码，使得在目的端所构建的全局乘积码的权重分布趋近于高斯分布。因此，目的端接收到的连续信息分组所形成的全局乘积码是码长很长且纠错能力强的码字。另外，本文对低复杂度的Chase II 译码算法[16]进行了改进，使之能应用于衰落信道上的协作编码场景。理论分析表明所构造的全局乘积码的权重分布趋于高斯分布，仿真结果也表明该方法能从空间上构造纠错能力强的全局乘积码，并且能使得整个协作系统获得良好的纠错性能。

2 系统模型

在如图1所示的一个无线网络中，协作传输分2个时隙完成。第一时隙，多个用户通过正交信道发送相互独立的数据分组。目的端接收到的信号可以表示为

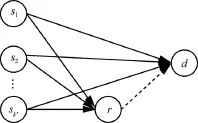
图1 网络拓扑结构

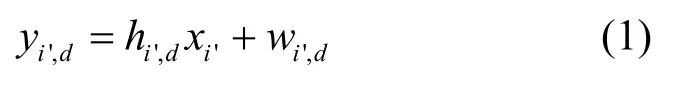
其中，i'∈｛1,2,…,k '｝表示发送源序号，yi',d是目的端接收到的来自于用户i'的信号，xi'是用户i'发送的符号，wi',d是均值为0，方差为的复高斯白噪声，hi',d是用户i'到目的端d的信道系数，并假设所有信道都服从均值为0，方差为1的平坦瑞利分布。中继接收到的信号yi',r的表达式类似于式(1)，在这不再赘述。第二时隙，中继对所接收到的信号进行处理，并转发处理后的信号xr给目的端，目的端接收的信号为

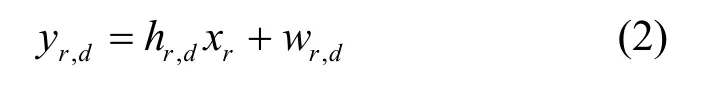
其中，yr,d为目的端接收到的来自于中继转发的信号，hr,d为中继到目的端的信道系数，wr,d均值为0，方差为的复高斯白噪声。最后，目的端对接收到的信号',idy和,rdy进行联合译码。假设接收端已知信道状态信息(CSI)，而发送端不知道CSI。并且假设用户离中继较近，则用户到中继的链路为理想信道。

3 网络乘积码

3.1 传统网络乘积码(CNPC)

协作中继系统分2个时隙交替完成。第一时隙，k'个源通过正交信道发送其信息分组给同一个目的端，信息分组是由参数为(n, k)系统线性分块码构成。第二时隙，中继对接收到的信息进行译码，然后按行来重新排列或交织，形成k'×k的矩阵，并且使用参数为(n',k')的系统线性分块码按列进行编码，然后转发底部n'-k'行的校验冗余位给目的端。如图2所示，目的端接收的信息可以构成(n,k)×(n',k')的乘积码。图2构造的码字是不完全乘积码，使用同样的方法易拓展到完全乘积码[6,9]。

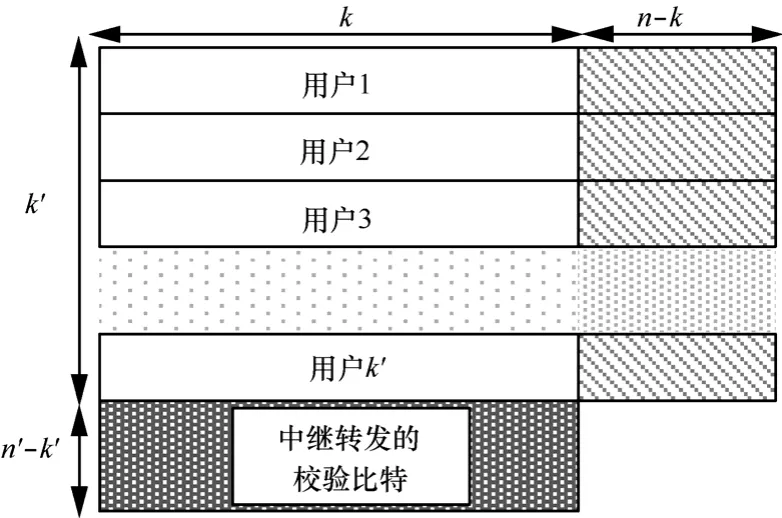
图2 网络乘积码结构

3.2 多元网络乘积码(MNPC)

不同于传统网络乘积编码中仅仅是机械地把分布式乘积码应用到协作网络中，本文提出的多元网络乘积码关键在于通过中继使用Turbo技术对译码后的源信息比特进行高码率编码。设Ci（i=0,1）是参数为（ni,ki,di）的系统线性分块码，其中，i=0和i=1分别表示源端子码序号和中继端子码序号。设K为信息序列长度ki的乘积，i=0,1。设πj(j=1,2,…,m-1)为交织器，其长度为未编码的源信息比特长度。目的端通过接收来自源端的子码C0和来自于中继端经交织器后再编码形成的m-1个子码C1的校验比特，从而构成一个m元的网络乘积码，设其为Θm。图3是中继端上的编码器结构的示意图，其中，aj（j=1,2,…,m -1）为使用子码C1对交织后信息比特高码率编码产生的校验序列，其长度为（n1-k1）K/k1。因此该m元网络乘积码Θm全局码长为

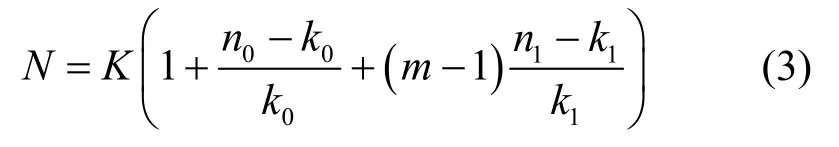
其码率为

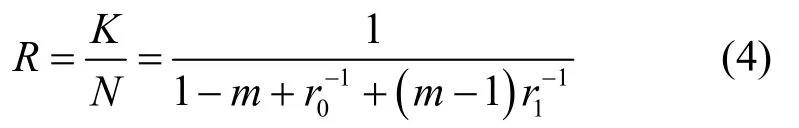
其中，ri=ki/ni是子码Ci的码率，并且趋近于1，i=0,1。

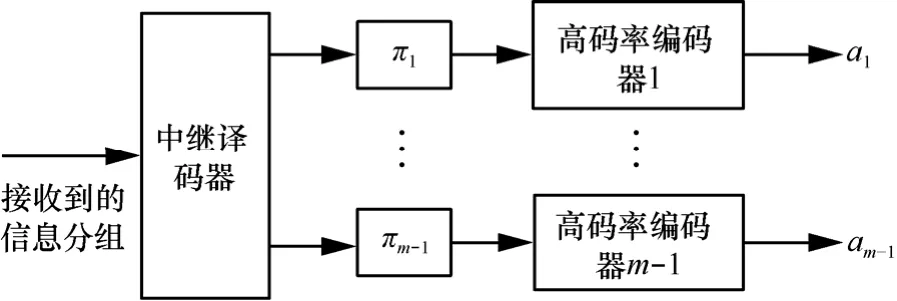
图3 中继端上的编码器结构

其中，⊗表示Kronecker 积，ki'=K/ki，Iki'是阶数为的单位阵。中继端子码的生成矩阵可以表示为

m元网络乘积码Θm的全局置换矩阵可以写为

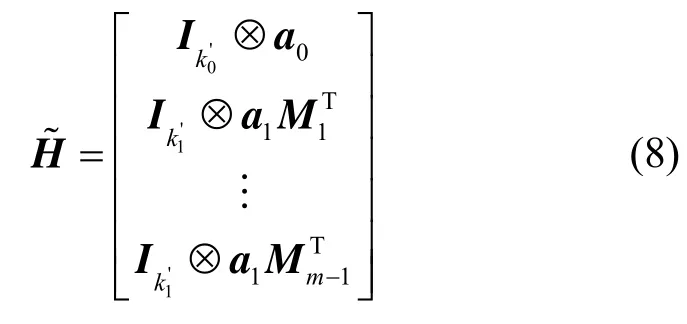
其中，ai是长度为ki的全1向量，0,1i=。为了保持m个子码的统计独立性，交织器应使得置换矩阵中的任何两行同一个位置同时为1的个数不超过1。

下面阐述所构建的m元网络乘积码可以实现近似高斯分布。首先回顾下Sidel’nikov理论[12]。

定理1

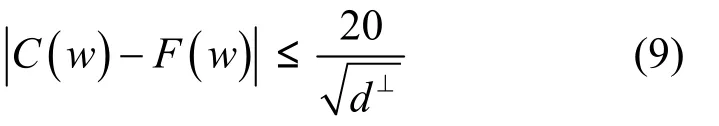
其中，C（w）和F（w）分别表示参数为(n,k,d)的码字C的权重累积分布函数和标准高斯累积分布函数，d⊥为码字C的对偶码的最小码重。

通过定理1可以得出m元网络乘积码具有近似高斯权重分布。

命题1 设m元网络乘积码Θm的子码全为汉明码，设ri(0,1)i=是参数为子码的码率，且设m(m＞1)为码字Θm的子码个数。如果，则m元网络乘积码Θm的权重分布随着ip→∞而近似高斯。

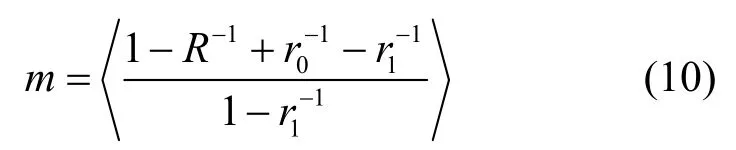
当m=1时，码字Θm的码率R和其对偶码码重分别随着ip→∞分别趋近于1和无穷，表明一个码长很长且码率很高的汉明码的权重分布也趋近于高斯分布。

使用类似的证明步骤，子码为汉明码的多元网络乘积码可以推广到子码为单奇偶校验码、BCH码、Alternate码和自偶码的多元网络乘积码，此类构造的码字且符合命题1前提条件的都具有近似高斯权重分布。由于篇幅有限，详细的证明不再赘述。值得注意的是后2种子码因其最小对偶码重满足趋近于无穷，对应的子码码率不为1，因此其所构造的多元网络乘积码的子码个数是有限的。

从命题1得知，具有近似高斯权重分布的多元网络乘积码的子码码率趋近于1，根据式(4)可得：该多元网络乘积码的全局码率也趋近于1，即该码字保持了如文献[15]提到的扩展单奇偶校验乘积码的高编码效率特性。

4 译码算法

目的端接收到2部分信息，一部分是来自于源端的yi',d信号，另一部分来自于中继的yr,d信号。然后目的端对接收到的信号yi',d进行相位幅度补偿，得到其中，i'=1,2,…,k '，对接收到的信号yr,d进行类似操作。接着进行软输入软输出译码算法，设为信号yi',dyr,d中的一个码字。

类似于Chase II 译码算法[16]，对于每个取值为±1的传输信息比特xj'，首先计算出其对数似然比为

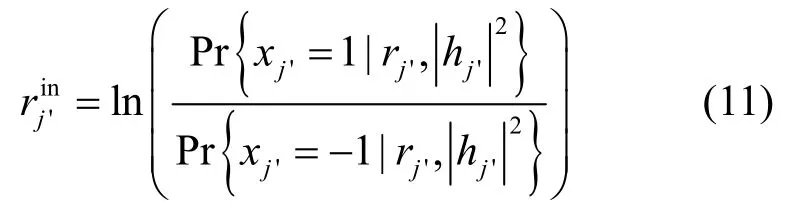
其中，hj'为传输信息xj'经历的信道系数。使用贝叶斯法则，得到

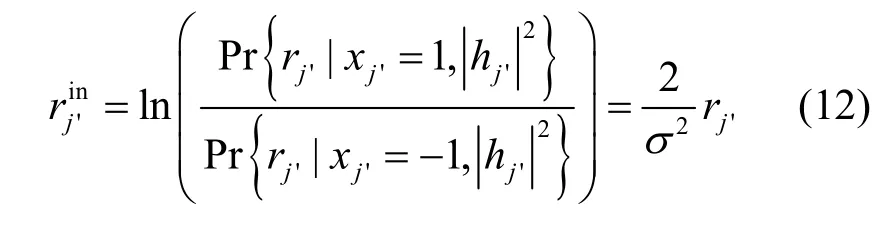
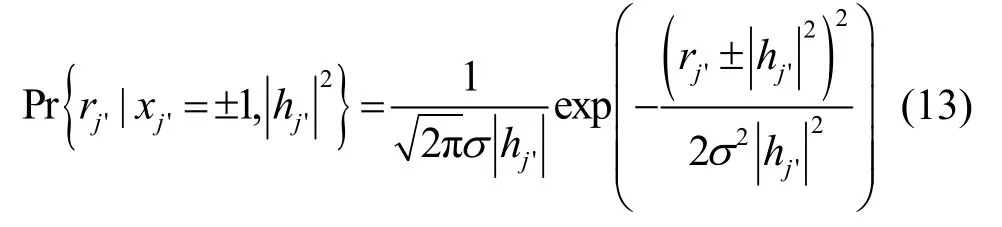
目的端通过计算获得码元的对数似然比后，将其排列成一个乘积码矩阵。译码器使用类Chase II 译码算法进行迭代软输入软输出译码。设为经历衰落后的一个码字的对数似然比，并且设为2p个测试序列中离接收序列最近的码字，其中，p为一个码字不可靠的码元数，可以根据码长设定。在高信噪比情况下，码元dj'的对数似然比为

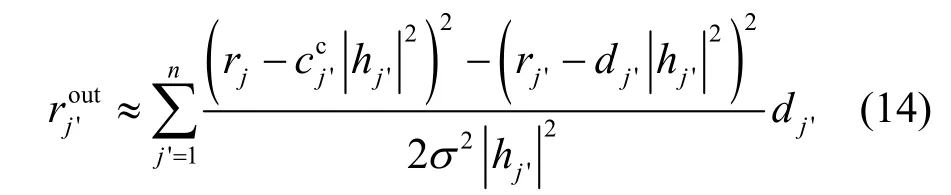
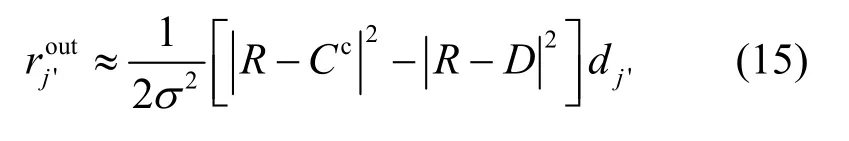
由式(15)和式(16)可得：译码器的输出外部信息可以表示为

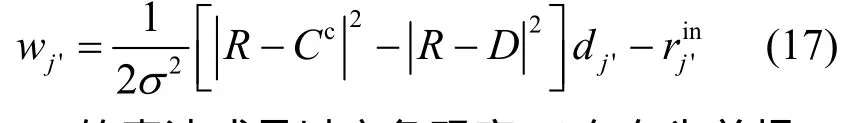
其中，wj'的表达式是以竞争码字Cc存在为前提，否则外部信息可表示为

其中，

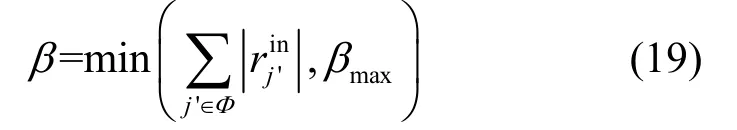
其中，Φ为输入码字的p个不可靠码元集合。具体迭代算法为：外部信息初始为0，即wj'（0）=0。然后编码器输入按如下进行更新：，其中，为信道输出的对数似然比，wj'（z-1）是上一步骤译码器输出的外部信息，参数α的设置参见文献[16]，z的最大值为迭代步骤次数(行或列)，βmax为可靠因子。

假设译码器已知式(15)中的σ值。为了减少参数α对乘积码译码的相关性，译码器输出的外部信息需归一化，即对于从用户端直达目的端的信号和从中继端转发到目的端的信号，式(15)分别相应地乘以

5 仿真结果与分析

本节对多元网络乘积码(MNPC)协作方法的性能进行蒙特卡洛仿真，并且与第3节描述的传统网络乘积码(CNPC)[6,9]和网络编码 (NC)[2]进行比较。中继端采用解码前传方式，调制方式为BPSK，源端发送的未编码的信息分组大小为572bit，发送功率均为1。所有信道服从参数为CN（0,1）的平坦瑞利分布，其中，CN表示循环对称复高斯随机变量。为了保证对比的公平性，相比较的MNPC和CNPC 2种协作方案都采用上节所提出的改进后的Chase II 译码算法，其中，参数βmax和迭代步骤次数(行或列)都设置为8，NC协作方案采用消息传递译码算法。源端采用的码字均为参数为(7,4,3)的汉明码，并且中继对译码后的源信息比特进行同样的交织后再编码，然后再转发产生的校验比特。下列仿真结果给出了CNPC、NC和MNPC 3种协作方案的误比特率(BER)随着用户到目的端直达链路信噪比的变化情况，图4和图5中为中继端到目的端链路信噪比。

表1列出了MNPC和CNPC码字的一些重要参数，为了公平性，它们的全局码率(0.4或0.47)保持近似相等。由于源端采用同样参数(7,4,3)的汉明码，则在2种对比方案中中继转发的校验比特数是一样的。表1同时也列出了一种NC码字的参数，源端也采用参数为(7,4,3)的汉明码，中继端先对接收到的信息比特进行异或(XOR)，然后转发，它的全局码率(0.38)是最小的，即中继转发的比特数目较前2种方案多。

如图4所示，在相同的全局码率下(0.40或0.47)，MNPC的误码率性能除了在低信噪比情况下均优于CNPC。当全局码率为0.40时，MNPC-I在信噪比大于2.5 dB的情况下，误码率性能好于CNPC-I，而MNPC-II在信噪比大于2.1 dB的情况下是最优的。这是由于中继上采用高码率编码通常需要高信噪比才能保证额外的性能增益。通过观察MNPC-I和MNPC-II的误码率曲线，图4同时也表明随着子码个数m和中继采用的子码码率的增加，MNPC所构造的码字的权重逐渐趋近于高斯分布，其误码率性能也得到显著增加，即验证了上文的理论分析。对比全局码率最小的NC协作方案，MNPC在误码率性能上仍然优于NC。

在实际场景中，中继信道一般好于源端到目的端的信道。为了比较MNPC和CNPC能否更有效地利用中继信道，在这引入一个信噪比差变量如图5所示，当G=10 dB时，对比图4，MNPC-I和CNPC-I的误码率性能曲线交叉点向左移，交叉点对应的信噪比从2.5 dB变成0.5 dB，表明MNPC能更加有效地利用中继信道。为了更进一步观察，表2统计了MNPC-I和CNPC-I的误码率性能曲线交叉点随着信噪比差G的变化情况。随着G的增加，交叉点对应的信噪比逐渐减小，即交叉点向左移。因此，相比CNPC协作方案，MNPC是一种能更有效利用中继信道来获得误码率性能提升的协作编码方法。若整个系统提供足够多的独立路径，从误码率曲线斜率可以看出，MNPC是一种分集增益加强技术。

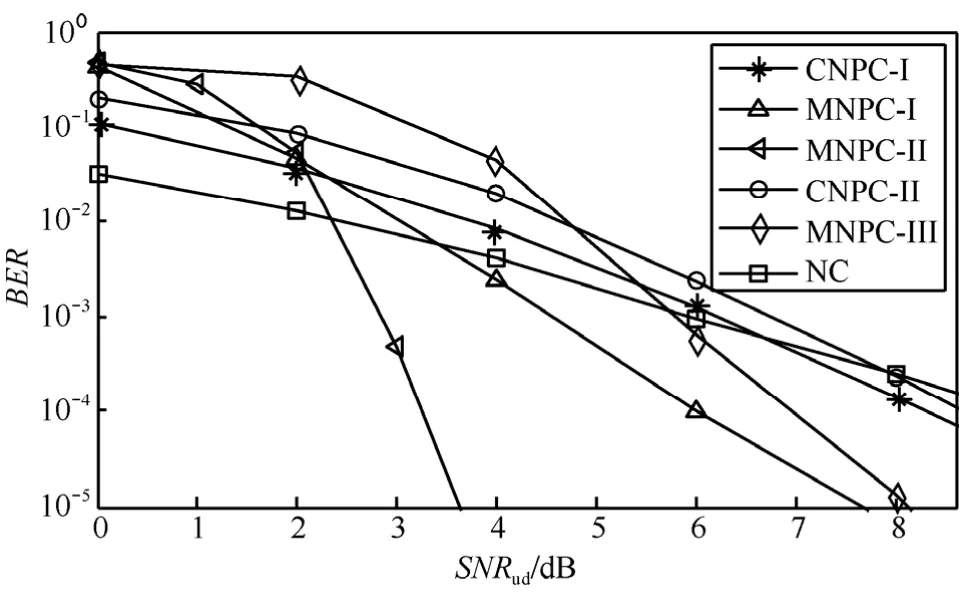
图4 MNPC、CNPC和NC的误码率性能比较

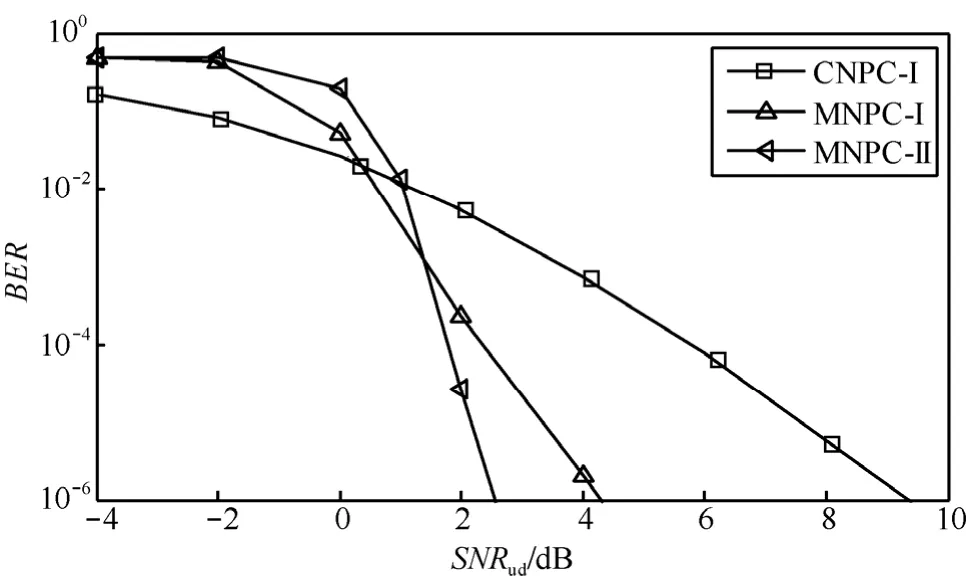
图5 中继信道增益对误码率的影响：MNPC和CNPC

表1 MNPC码字和CNPC码字的参数

表2 MNPC和CNPC误码率曲线交叉点对应的信噪比

6 结束语

本文基于协作中继场景下提出了一种多元网络乘积码，以代数形式描述该码字在空间上的构造方法，并且对Chase II 译码算法进行了改进，使之能适用于衰落信道环境中的分布式编码。理论分析结果表明了所构造的多元网络乘积码的权重分布趋近于高斯分布，仿真结果也验证了该方法能显著地提高误码率性能。

[1] AHLSWEDE R, CAI N, LI S Y R, etal. Network information flow[J].IEEE Trans on Info Theory, 2000, 46(4):1204-1216.

[2] CHEN Y, KISHORE S, LI J. Wireless diversity through network coding[A].Proc IEEE Wireless Commun and Networking Conf (WCNC)[C]. Las Vegasm, NV, USA, 2006. 1681-1686.

[3] ZHANG Z. Theory and applications of network error correction coding[J]. Proceedings of the IEEE , 2011, 99(3):406-420.

[4] JODA R, LAHOUTI F. Network code design for orthogonal two-hop network with broadcasting relay: a joint source-channel-network coding approach[J]. IEEE Transactions on Commun, 2012, 60(1):132-142.

[5] BAO X, LI J. Adaptive network coded cooperation (ANCC) for wireless relay networks: matching code-on-Graph with network-on-Graph[J]. IEEE Trans Wireless Commun, 2008, 7(2):574-583.

[6] AHSIN T U R, SLIMANE S B. Network coding based on product codes in cooperative relaying[A]. Proc IEEE Wireless Commun and Networking Conf (WCNC)[C]. Sydney, Australia, 2010. 1-6.

[7] ZHANG J Y, LETAIEF K B, FAN P Y. A distributed product coding approach for robust network coding[A]. Proc IEEE Int Conf on Commun (ICC)[C]. Beijing, China, 2008. 176-180.

[8] XIA Z S, QU Y, YU H, etal. A distributed cooperative product code for multi-source multi-relay single-destination wireless network[A]. 15th Asia-Pacific Conf on Commun[C]. Shanghai, China, 2009. 736-739.

[9] ZAFAR B, SLIMANE S B, JAVED M U. Network product coding[A].Proc IEEE Consumer Commun and Networking Conf[C]. Cape Town,South Africa, 2010. 1-5.

[10] LI Z Y, PENG M G, WU Z J, etal. Network coding scheme based on LDPC product codes in multiple-access relay system[A]. Proc IEEE Int Conf on Commun (ICC)[C]. Kyoto, Japan, 2011. 1-4.

[11] OBIEDAT E A, CAO L. Soft information relaying for distributed turbo product codes (SIR-DTPC)[J]. IEEE Signal Processing Lett,2010, 17(4):363-366.

[12] CAIRE G, TARICCO G, BATTAIL G. Weight distribution and performance of the iterated product of single-parity-check codes[A].IEEE Global Telecommun Conf (GLOBECOM)[C]. San Francisco,USA, 1994. 206-211.

[13] BIGLIERI E, VOLSKI V. Approximately Gaussian weight distribution of the iterated product of single-parity-check codes[J]. IEEE Electronics Lett, 1994, 30(12):923-924.

[14] YUE D W, YANG E H. Asymptotically Gaussian weight distribution and performance of multicomponent turbo block codes and product codes[J]. IEEE Trans on Commun, 2004, 52(5):728-736.

[15] SHIOZAKI A, KISHIMOTO M, MARUOKA G. Close-to-capacity performance of extended single parity check product codes[J]. Electronics Letters, 2011, 47(1):34-35.

[16] PYNDIAH R M. Near-optimum decoding of product codes: block turbo codes[J]. IEEE Trans on Commun, 1998, 46(8):1003-1010.