基于商空间的层次式数据网格资源调度算法
2013-01-07夏纯中宋顺林
夏纯中,宋顺林
(1.江苏大学 计算机科学与通信工程学院,江苏 镇江 212013;2.江苏大学 信息化中心,江苏 镇江 212013)
1 引言
近年来,数据网格凭借其强大的扩展能力被用于构建企业级数据库云平台。例如,大型医疗集团信息集成平台[1]利用数据网格对集团内各医疗机构分布异构的医疗信息数据库进行集成和共享;红帽发布的JBoss Enterprise Data Grid[2]更是将数据网格作为其企业云计算战略的重要基础构件。层次式数据网格是一种常见的数据网格架构,由于大规模分布式系统具有小世界特性,用户在对数据的使用上呈现出社团性和层次性,即特定区域内的用户只对特定部分的数据最感兴趣,而层次式数据网格可以很好满足这一需求。
在企业应用领域,用户对数据网格的服务质量(QoS,quality of service)有着和科学计算截然不同的需求。网络连接带宽和不同网格节点处理能力的差异导致数据网格无法像传统的企业数据中心那样为业务系统提供实时、可靠的数据服务。层次式数据网格资源调度的目的就是为网格中各节点和不同级别业务分配带宽,保障各级业务的服务质量,并使系统整体资源利用率最优。
层次式数据网格资源调度可以采用现有的数据网格调度算法,常见的数据网格调度算法大致分为 4类。1) 基于综合指标直接选择法。Cheng[3]提出一种基于Min-Max的负载均衡算法,将文件和网络带宽分为Min和Max 2类,调度时根据文件所属类别到相应站点下载。Mistarihi等人[4]使用响应时间、可靠性和安全构成一个评价指标,并使用层次分析法确定各指标的权重。Du等人[5]提出了一种基于可靠度的指标来减少任务完成时间和执行代价。Qu等人[6]提出网络负载和服务容忍度 2个目标函数,使用权重因子平衡2个目标函数。Tang等人[7]提出一种副本价格模型,模型综合考虑了CPU、内存、网络的延时、带宽和可靠性等多种因素,并通过拍卖协议选取传输代价最小的副本。2) 基于机器学习法。文献[8,9]都采用神经网络构建数据传输时间预测模型,使用日志数据中不同大小文件在不同网络带宽下的传输时间作为样本对模型进行训练。文献[10]采用k-NN算法对不同节点磁盘IO和网络延时下的文件下载时间进行学习。文献[11]中,Almuttairi等人提出基于K均值聚类对站点进行分类,采用基于灰度的粗糙集理论解决安全、可靠性、成本和响应时间等属性不确定的问题。3) 基于时间序列法。Li等人[12]使用灰色理论预测副本响应时间,并使用马尔科夫链预测副本的可靠性。Wu等人[13]提出一种状态模糊评估策略,并使用灰色GM(1,1)模型动态地预测服务时间。4) 基于进化计算法。Munoz[14]提出基于粒子群优化算法,根据网络延迟和带宽确定传输代价,使用访问率和传输代价作为最优化评价函数。Xiong[15]提出了副本选择算法的 QoS模型,采用层次分析法分析不同 QoS指标的重要程度,并以此作为不同指标的权重向量。提出了一种基于MapReduce的并行遗传算法加速运算。算法主要考虑3个QoS指标,即平均传输率、平均带宽和可靠性。直接使用上述算法对层次式数据网格进行调度时,由于算法中所有节点均在同一层面,当网格节点数量很大时,极易出现以下2个问题:①算法难以保证系统全局最优,这主要是由于算法缺少在不同粒度、不同层面上对网格流量进行调度,没有充分利用层内和层间节点对不同优先级的任务进行优化。②数据网格资源调度问题属于NP问题,当网格内节点的数量较多时,全局资源调度算法收敛过慢,难以满足企业应用对数据实时性的要求。
粒计算是一种通过对复杂问题进行粒化分解,从而降低问题复杂度的方法论,它是模拟人类在解决复杂问题时能够由粗至细,多层次地观察和分析问题的能力。张铃和张钹提出使用商空间理论对粒度空间进行描述。商空间理论通过保真原理和保假原理在论域元素上构造一系列不同粒度的商空间,形成一个分层递阶的商空间链,从而简化原始问题的求解[16]。
本文首次引入粒计算的思想解决传统数据网格资源调度算法在调度层次式数据网格时存在的问题,提出了一种基于商空间的层次式数据网格资源调度 QSHDGRA(quotient space theory based hierarchical data grid resource allocation)算法。其主要创新在于:采用商空间粒度计算的方法在不同粒度层面对数据网格系统流量进行调度,保障不同优先级业务的QoS的需求,此外调度算法还兼顾了数据网格整体节点负载和网络流量的均衡,实现了系统资源利用的全局最优化。
2 层次式数据网格模型
2.1 体系结构
层次式数据组织是一种常见的数据管理方式。如图1所示,在层次式数据网格中,所有节点组成一个层次化的树状网络,根节点拥有全部数据副本,根节点将所有数据副本平均分配到各个二级节点,二级节点再将数据副本平均分配到下属的三级节点。一级节点定期监控各节点和各条链路的负载情况,采用特定算法分配各个节点的处理带宽的能力,实现系统访问性能的全局最优化。
为了满足企业应用集成领域中不同业务 QoS的要求,将数据网格的业务请求分为3种QoS级别:第一类业务优先级最高,要求能够立即响应;第二类业务优先级为中,允许在一定时间内完成响应;第三类业务优先级最低,当系统繁忙时,可以暂停响应。
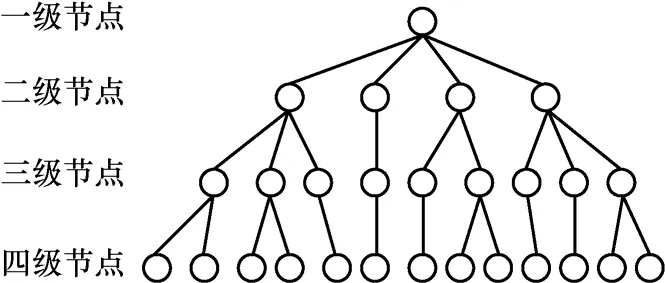
图1 层次式数据网格节点组织
层次式数据网格有以下3个优点。1) 网格数据具有高可靠性。根节点和各级节点的数据互为异地备份。每一个数据均有3个副本,且副本互为异地备份。2) 网格系统具有很好的容错性。任何节点的单点故障都不会影响系统运行。例如,当根节点发生故障时,其他副本节点可继续为用户提供数据访问服务。3) 网格系统具有负载均衡能力。根节点和各级节点构成一个分布式虚拟集群。当某个节点或某条路径访问负载过高时,系统会自动地将访问请求分配到其他节点上。
2.2 问题形式化定义
在层次式数据网格有向图G(V,E)中,采用M/M/1排队模型定义系统资源调度问题。
定义1(节点请求平均等待时间)。单位时间内到达节点j的请求数为λj,节点j的处理能力为μj,则节点j的平均请求等待时间为Tj为
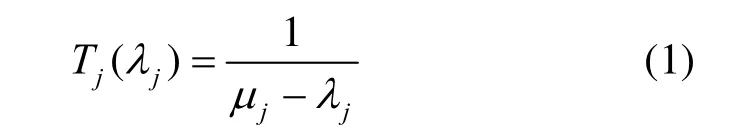
定义2(节点资源利用率)。设Sj为单位时间内到达节点j的请求数占其最大处理能力的比例,则该节点资源利用率为

定义3(网络资源利用率)。设从节点i出发经过路径pij到达节点j的请求数为λij,从节点j出发经过路径pij到达节点i的请求数为λji,路径pij的最大吞吐率为lij,则路径pij的网络资源利用率为
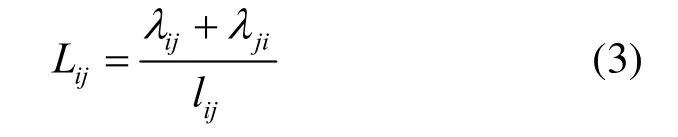
定义 4(请求流量矩阵)。用请求流量矩阵(λQoSm,ij)N×N(m=1,2,3)表示系统内从节点i出发到达节点j的不同QoS级别流量的分配情况。3种QoS级别流量矩阵相加,即为节点i到j的流量。
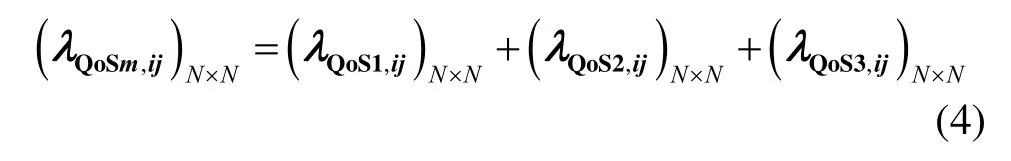
定义5(系统资源调度的多目标优化问题)。层次式数据网格系统资源调度问题可以分为以下 3个子问题:一是为不同QoS级别用户分配带宽,使用户平均请求等待时间最小化;二是节点负载利用率最大化。即充分利用冗余节点实现请求负载均衡,避免请求过分集中到某些节点上;三是网络流量利用率最大化。即充分利用空余网络链路,避免造成某些路径流量过大,而另外一些路径却未充分使用。
综上所述,系统资源调度的全局最优化目标为确定请求流量矩阵(λQoSm,ij)N×N使得不同 QoS级别业务的平均请求等待时间最小化,同时实现节点资源利用率和网络资源利用最大化。

式(6)和式(7)使用信息熵衡量网格中节点负载的均衡度和路径流量的均衡度。第一个约束条件表示系统请求流量守恒,第二个约束条件表示节点负载分配后的流量守恒,第三个约束条件保证队列平均长度不会无限增大。
定义6(全局最优目标调和函数)。采用线性加权和法将定义5中的多目标问题转换为单目标问题,定义层次式数据网格系统全局最优资源调度目标函数为
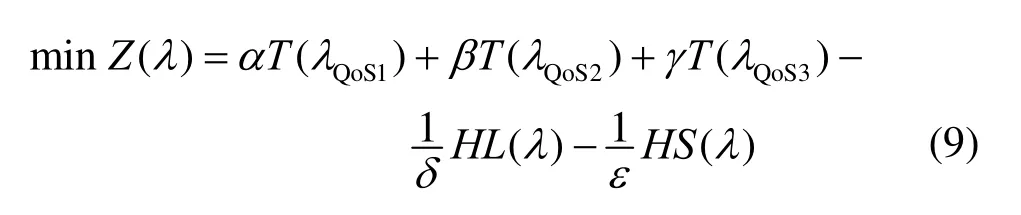
式(9)是系统中各 QoS用户请求的平均等待时间和网络与节点资源利用均衡度的调和函数。
3 基于商空间的资源调度算法
3.1 传统优化算法及其弊端
本文的最优化问题是一个非线性规划问题,且属于NP问题,采用启发式计算的方法可以快速获得最优解。粒子群算法是一种常用的基于进化计算的启发式算法,其主要特点是个体数目少,计算简单,顽健性好和可并行计算。使用粒子群算法首先要确定粒子的编码方式和适应度函数。本文以数据网格节点间的有向连接数作为解空间维度,每一维对应一条有向连接,其取值为分配给该连接的请求流量。每个粒子对应的D维向量X表示系统资源调度问题的一个解,适应度函数为式(9)所定义的目标函数。
粒子群算法在求解本文最优化问题中暴露出以下的弊端:由于问题的解空间的向量维度太大,使得算法收敛到全局最优值的速度非常缓慢, 并且极易陷入局部最优值。
3.2 基于商空间的优化算法
在层次化网格中,随着网格节点数目的增多,节点间的连接数量呈几何级数增长,网络拓扑结构越来越复杂,资源调度算法的搜索空间也越来越大。本文的主要思想就是使用粒度计算的思想来简化求解层次化网格最优资源调度问题的复杂度。通过对原始最优化问题进行层层分解,在不同粒度、不同层面上对问题进行优化,以求加快求解速度,并获得全局最优值。
3.2.1 构建商空间
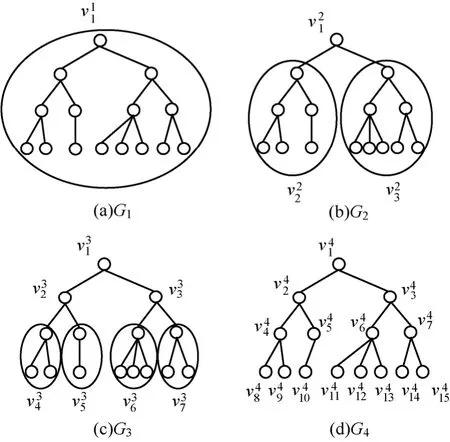
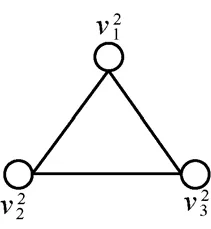
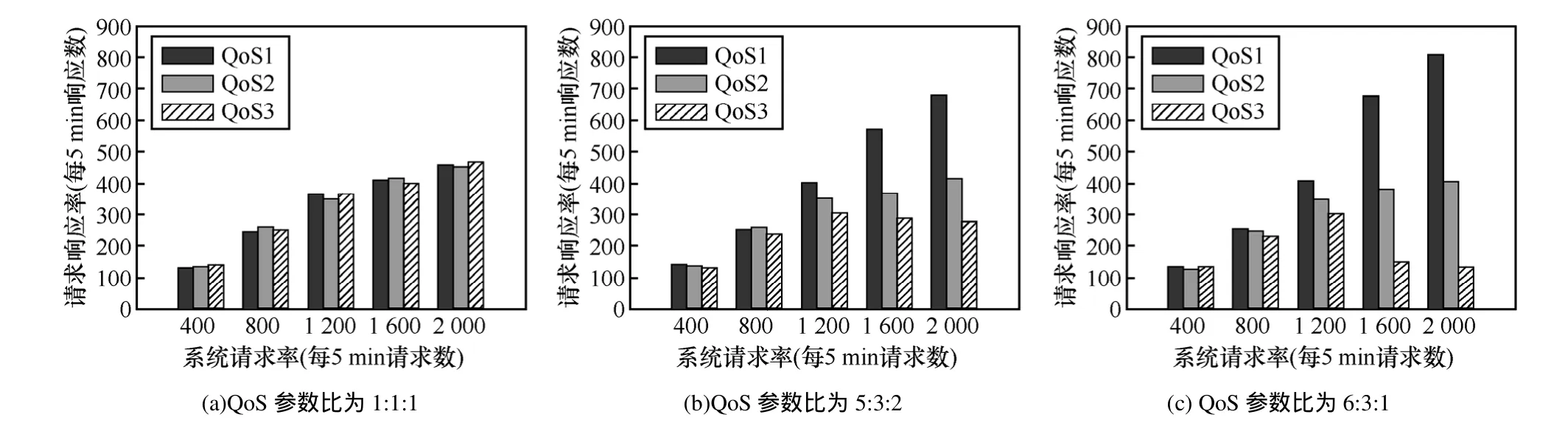
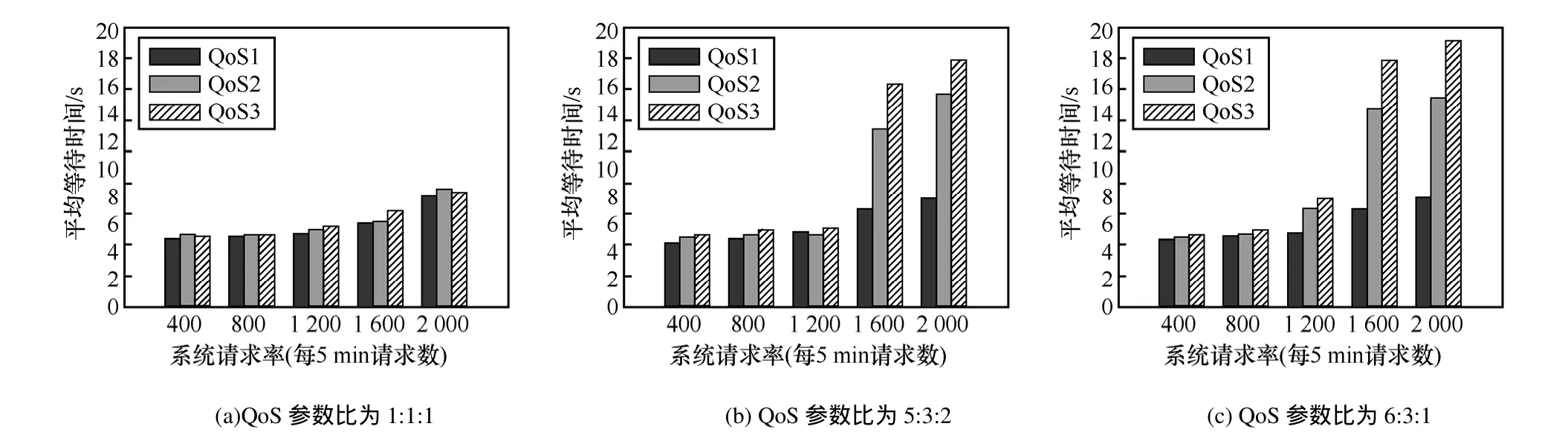
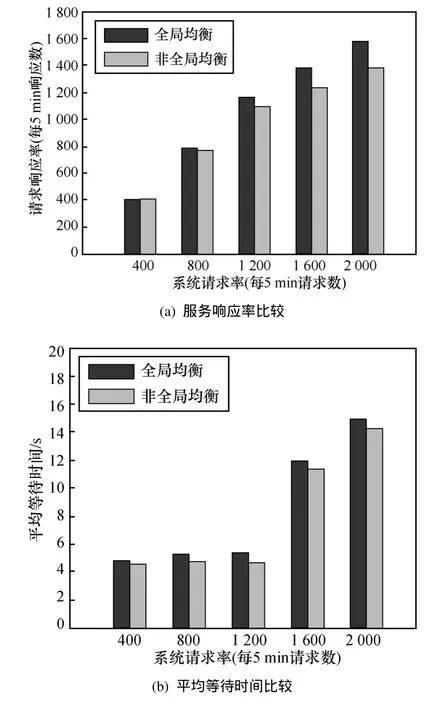
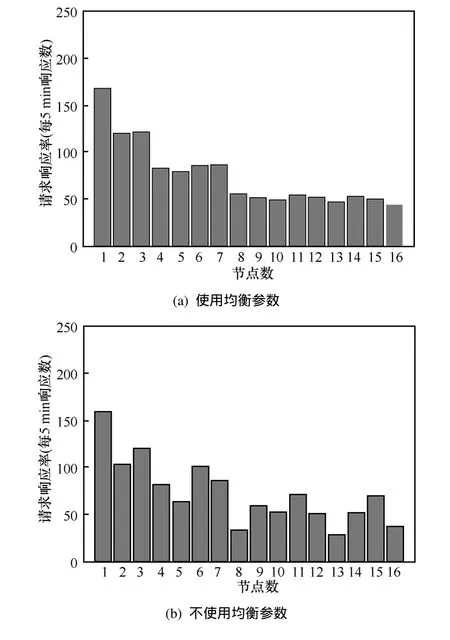
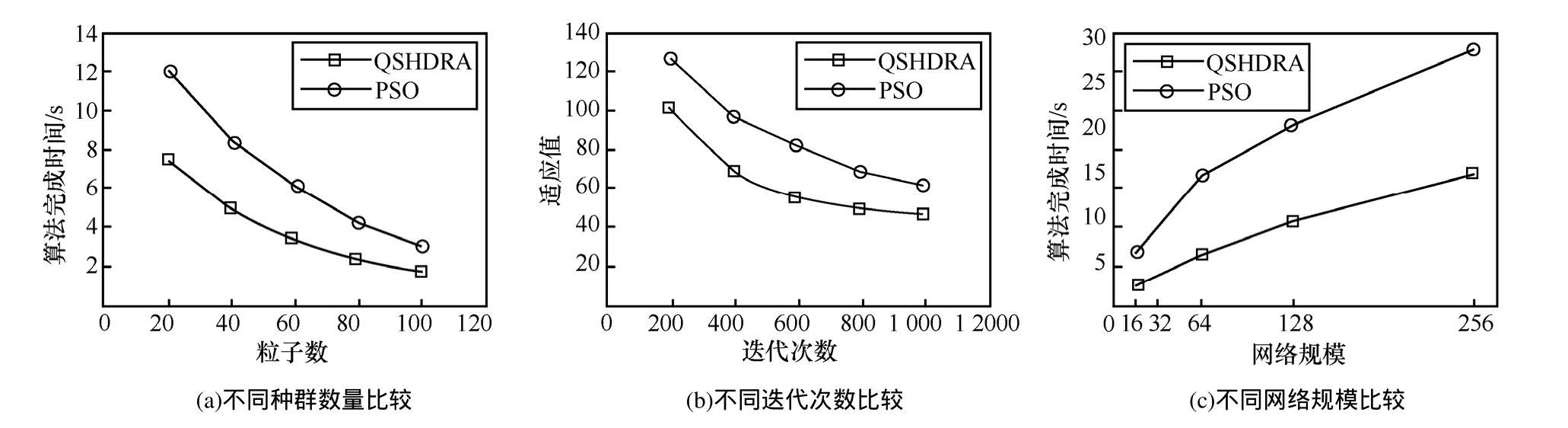
给定一个L层的层次网格的网络图G(V,E),用l(v)表示节点所属的层次。根节点属于第一层,即l1=1,其余各层次关系为l1<…< lk… 定义7等价关系R(lk)。 该等价关系的实质是将某一级节点及其各自所有子节点看作一个整体,即一个粒子,和上级节点归为同一等价类。当li从1增大到k时,可以在各个级别层次上构建不同粒度的网络拓扑,形成分层递阶的商空间链。 3.2.2 资源调度算法 基于商空间的层次式数据网格资源调度算法形式化定义如下。 问题:给定层次式数据网格G(V,E),确定其上的各优先级业务的最优请求流量矩阵(λQoSm,ij)N×N,使得系统全局资源调度目标值Z(λ)最小。 算法步骤描述如下。 1) 构建商空间。输入原始层次化网格模型G,给出网络节点数量V,网络拓扑结构E,各连接链路最大负载L和节点的最大负载S。根据网络层次结构确定等价关系R,并构建分层递阶商空间链G1>G2>… >GL。 2) 确定求解最优化算法的粒子群规模m和算法参数,包括惯性因子w、学习因子c和速度限值S。设定最大迭代次数n和迭代终止阈值ε。 3) 由于G1是将全体节点看作一个整体,没有进行划分,因此从第二层商空间开始进行递归求解。设k=2,转到4)。 4) 在商空间Gk中,根据节点数量Vk和连接数量Ek构建流量矩阵作为解向量Xk。使用粒子群算法完成一次搜索,求得本层粒子的一个最优解。查看该空间是否有更细粒度的空间,如果有转到5),否则转到6)。 5) 进入更细一层商空间Gk+1,构建流量矩阵,由于上一层空间的搜索有陷入局部最优值的可能,因此本层使用2个粒子群按照不同的策略进行搜索。第一个粒子群中增加上一层空间求得的最优解作为本次求解的约束条件,即由上一层粒子分解而得的各粒子负载之和不能超出上一层粒子获得的最优分配值。第二个粒子群则不增加约束条件进行搜索。当2个粒子群分别完成最优化搜索之后,比较其最优解。如果不加约束条件的粒子群获得的解更优,则将该解合成为上一层空间的最优解,重复步骤5),跳转到上一层空间重新搜索。如果加了约束条件的粒子群获得的解更优,则该最优解为本层粒子的最优解。查看本层是否有更细粒度的空间,如果有继续5),跳转到下一层空间进行搜索,否则转到6)。 6) 此时已完成最细一层商空间,得到原始网络空间的资源分配流量矩阵λQoSm。系统根据最优值定义的请求流量矩阵调度各级QoS业务请求流量。 3.2.3 算法实例 下面结合一个例子来阐述算法过程,给出如图2所示的层次化网络。网络共有15个节点,为了便于描述,网络采用树状结构。 图2 商空间构建过程 原始网络中所有节点全体G1作为初始商空间,节点集记为V1。 首先使用等价类R(2)对原始空间进行划分,得到商空间G2,其商集V2如下。 这样原始空间划分成包含3个元素的粗粒度网络图,其边集合为 (V2,E2)构成商空间G2,其拓扑结构如图3所示。 图3 G2商空间拓扑结构 其流量分配矩阵为 接下来,使用等价类R(3)对G2进行划分,得到商空间G3,其商集V3如下。 其流量分配矩阵为 同样,使用 2个粒子群算法求得G3空间中的最优解,第一个粒子群需要满足G2空间已经求得的最优解的约束条件,即 最后,使用等价类R(4)对G3进行划分,得到最细粒度的商空间G4,其商集V4如下 由于该空间等同于原始问题空间,其求得最优解就是原问题的最优解。 3.3.1 命题证明 命题 1对于层次式数据网格采用基于等价关系构建的分层递阶商空间链,可以求得原始问题的最优解。 证明对于原始网络,商集[X]中的元素就是各个节点,商结构[T]是原始网络拓扑,假设商空间链有L层。原始问题存在最优解,即在分层递阶商空间链中,最细粒度的空间([XL], [TL])存在最优解。采用等价关系R(L-1)对其进行划分,得到上一层商空间([XL-1], [TL-1]),根据商空间的保真原理可知该空间中必包含原始问题的最优解。反复应用商空间保真原理可得最粗粒度商空间([X2], [T2])存在最优解。由此可得原始空间最优解必包含在各级空间的最优解中,因此基于分层递阶商空间链逐层搜索可以求得原始问题的最优解。 命题 2在分层递阶商空间中求解的过程,是一个逐步逼近最优解的过程。 证明采用反证法。假设在某一粒度的空间([XL], [TL])中,求得一个当前最优解,在该粒度空间最优解的约束下,更细粒度的下级空间([XL+1],[TL+1])可以得到一个更优解。假设该解不是最优解,说明超出上级空间约束还有最优解,将该最优解的分量相加,由保真原理得到上级空间解就比之前求得的最优解更优,与之前的解是最优解的假设矛盾。 由此命题可以得出,如果要求出全局最优解,那么每一层的解都必须是当前层内的全局最优解。故此在算法中采用了双粒子群,一个粒子群基于约束条件搜索,另一个粒子群不受约束搜索,这样可以充分保证解空间的完备性。 3.3.2 收敛性分析 分析 QSHDGRA算法收敛性需要用到 Solis的随机优化算法以概率1收敛于全局最优解的充分条件。 命题3假设QSHDGRA求解的目标函数f是可测函数,其解空间S为可测集,那么,QSHDGRA算法以概率1收敛于全局最优解。 证明由Solis收敛定理知,只需证明QSHDGRA满足Solis收敛假设1和假设2即可。 1) QSHDGRA算法中商空间由粗到细的搜索过程是一个对搜索空间逐步压缩的过程,每一层搜索的最优值逐步逼近全局最优值。迭代函数f可归结为 其中,t为进化代数,算法的解序列为可以保证其趋向最优值,因而容易证明其满足Solis收敛假设1。 2) 设各个粒度网络中最优解的样本空间的并必包含S,即其中Mi,t为第t代粒子i的样本空间支撑集。QSHDGRA算法在每一层空间采用2个粒子群进行搜索,第一个粒子群保证搜索空间的收敛,第二个粒子群将保证种群多样性,随机搜索空间而不进行收敛,设第一个粒子群支撑集的并集为α,第二个粒子群支撑集的并集为β。由于第二个粒子群搜索的随机性,必然存在整数t1,使得当t>t1时,β⊇S。因此,对于QSHDGRA算法,存在整数t2,使得t>t2时的任意 Borel子集A=Mi,t,则有v(A)>0,所以QSHDGRA算法满足Solis收敛假设2。 综合1)和2),由Solis收敛定理可得QSHDGRA算法是一个全局收敛算法,能以概率1全局收敛。 3.3.3 复杂度分析 粒子群算法的收敛速度与其解空间规模相关,给定网络G(V,E),节点数量为n,解空间维度为m=n(n-1),则收敛的时间复杂度为O(sm),其中s为解向量中每一维度的取值范围。基于等价关系商空间模型构建L层分层递阶的商空间链G1>G2>…>GL。设在商空间Gk中,解空间维度为mk,算法收敛的时间复杂度为,则整个算法的时间复杂度为在算法求解过程中,虽然解空间维度逐步增大,即m1<m2<…mL,但由于搜索空间不断减小,每一维度的取值范围也逐步减小,即s1>s2>…sL,因此最优情况下,算法能够以几何速度收敛。 仿真实验采用GridSim仿真软件。仿真网络拓扑如图2所示:一级节点,即根节点1个;二级节点2个,采用100 Mbit/s专线和一级节点链接;三级节点4个,采用50 Mbit/s专线连接到所属的二级节点;四级节点8个,采用10 Mbit/s专线连接到所属的三级节点。各节点内部网络是1 000 Mbit/s网络,各节点之间均采用虚链路实现路由连通。仿真文件大小为 1~5 MB之间的随机值,系统共产生1 000个文件,按层次关系分布到各个节点中。系统采样单位时间为 5 min,即300 s,系统请求率为每单位时间生成的请求数,节点处理能力的单位为每单位时间处理的事务数,四级节点的最大处理能力分别为300、200、120和80。 实验包含4个部分:首先分析了不同QoS参数对不同QoS服务吞吐率和响应时间的影响;其次分析了全局均衡参数对系统整体性能的影响;接着分析了算法在不同种群数量、迭代次数和网络规模下的收敛速度;最后将本文的 QSHDGRA算法和MinTime最小时间算法、Random算法的性能进行了横向比较。 首先比较不同 QoS参数对不同级别业务的吞吐率和平均响应时间的影响。对式(9)中的均衡参数δ和ε取零,分别考察α:β:γ为1:1:1,5:3:2和 6:3:1 3种情况下性能差别。 从图4和图5中可以看出,随着系统请求率由400增大到2 000,服务响应率也相应地由400增加到1 370。当系统请求率小于800时,系统处于轻载,所有的请求基本都能够及时响应,不同QoS参数比下的3种业务的吞吐率大致相同,平均等待时间也大致相等。当系统请求率增大到1 200时,系统负载加大,不同QoS参数比下的3种业务吞吐率出现明显差异。当α:β:γ=1:1:1时,3种业务的吞吐率仍然保持大致相当,但当α:β:γ=5:3:2 和α:β:γ=6:3:1时中,3种业务的吞吐率依次减少,业务平均等待时间依次增加。当系统请求率大于1 600时,已经接近系统的满载负荷,第一种参数比下 3种业务吞吐率仍然近似相等,而后2种参数比下的吞吐率大致比例为5:3:2和6:3:1,且第二、三类业务的响应时间明显大于第一类业务。由此可见,QSHDGRA 算法通过调节参数α:β:γ可以控制不同优先级业务的流量,从而保障高优先级业务的吞吐率和相应时间约束。 图4 不同QoS参数比时各级别业务吞吐率比较 图5 不同QoS参数比时各级别业务平均等待时间比较 本节分析全局均衡参数对系统性能的影响,即式(9)中的均衡参数δ和ε对系统吞吐率和平均等待时间的影响,公式中α:β:γ取固定值5:3:2。 从图6(a)中可以看出,随着系统请求率逐步增大,使用均衡参数比不使用均衡参数可以获得更高的响应率,即使在系统重载时,仍可以进一步提升响应率。从图6(b)中可以看出,在系统轻载时,两者的平均响应时间大致相当,当系统重载时,使用均衡参数时平均响应时间会略大,这是由于平均响应时间在目标函数中的比例已经降低,系统向着全局吞吐率更大的目标进行优化。 图6 使用和不使用均衡参数下吞吐率和平均等待时间的比较 图7显示了使用均衡参数和不使用均衡参数时各节点服务响应率的差别。此时系统请求率为1 200,处于轻载状态。从图中可以看出,使用均衡参数和不使用均衡参数相比,各级节点的负载更加平均。由此可见,全局均衡参数可以很好地平衡各个节点的工作负载,有效避免某些节点处于繁忙状态,而另一些节点处于空闲状态,从而进一步提升系统整体的吞吐率。 图7 使用和不使用均衡参数下各节点服务响应率比较 本节分析 QSHDGRA算法和不使用商空间的PSO算法在不同种群数量、迭代次数和网络规模对算法收敛速度的差别。 从图 8(a)中可以看出,粒子群的种群数量由20增大到100时,QSHDGRA算法的收敛速度快于PSO算法,不过当种群数量大于60后,速度减少的幅度也相应减小。在图8(b)中,当迭代次数由200增加到1 000时,QSHDGRA算法比PSO算法得到的适应值更优,且可以更快地收敛到最优值。综合图 8(a)和 8(b)可得,种群数量为 60,迭代次数为600时,系统可以在可接受的时间内获得近似的最优值。图8(c)显示了网络规模扩大时,算法计算时间的变化。当网络规模由15个节点增大到255个节点时,QSHDGRA算法的计算时间近似为PSO算法的一半,这是因为QSHDGRA算法可以利用商空间迅速收敛到最优值,因此计算时间可以保持近似线性增长。 将本文的QSHDGRA算法和MinTime最小时间算法、Random算法的性能进行比较。MinTime最小时间算法在搜索副本节点时仅仅以最快完成时间为目标,Random算法则是随机从副本节点中选择一个节点获取数据。从图9(a)和图9(b)中可以看出,当请求率在 800以下时,系统处于轻载,3种算法的效率差别并不显著,QSHDGRA算法的吞吐率略优于其他2种算法。随着请求率增大到1 200时,3种算法效率出现明显差别,MinTime算法最差,QSHDGRA算法最优,而Random算法位于两者之间。此时由于系统尚未满载,三者的平均等待时间差别仍然近似相当。当请求率达到2 000时,系统处于重载时,QSHDGRA和其他2种算法的差别进一步拉大。Random算法之所以优于MinTime算法是因为随机选择进度可以在一定程度上对实现节点的负载均衡,而QSHDGRA算法由于兼顾了系统整体节点处理能力和网络能力的均衡性,虽然响应时间略大于其他2种算法,但吞吐率也显著优于其他2种算法。 图8 不同种群数量、迭代次数和网络规模下算法收敛速度比较 图9 QSHDGRA算法与其他算法性能比较 本文针对传统数据网格调度算法在对层次式数据网格调度时出现的难以得到全局最优值和收敛速度过慢问题,提出了一种基于商空间的层次式数据网格资源调度算法。定义了基于不同QoS业务请求的平均等待时间和网络与节点资源利用均衡度的调和模型的目标函数,实现了基于商空间的层次式最优资源调度算法。仿真结果表明,该算法可以显著提升系统的吞吐率,加快收敛速度,并具备线性扩展能力。本文提出的算法虽然具备分布式调度的特性,但仍然属于一种全局控制算法。当全局调度节点不可用时,各节点如何分布协同实现资源调度将是下一步主要的研究方向。 [1] ZHANG J G, ZHANG K, YAN Y Y,et al.Grid-based implementation of XDS-I as part of image-enabled EHR for regional healthcare in Shanghai [J].International Journal of Computer Assisted Radiology and Surgery, 2011, 6(2):273-284. [2] JBoss enterprise data Grid[EB/OL].http://www.jboss.com/edg6-earlyaccess/, 2012. [3] CHENG K Y, WANG H H, WEN C H,et al.Dynamic file replica location and selection strategy in data grids[A].Proceedings of the 1st IEEE International Conference on Ubi-Media Computing and Workshops[C].Lanzhou, China, 2008.484-489. [4] AL-MISTARIHI H H E, YONG C H.On fairness, optimizing replica selection in data grids[J].IEEE Transactions on Parallel and Distributed Systems, 2009, 20(8):1102-1111. [5] DU W, CUI G H, LIU W.Reliability-aware replica selection for data-intensive applications on data grids[J].Information an International Interdisciplinary Journal, 2011, 14(12):3913-3920. [6] QU M C, WU X H, LIAO M H,et al.A novel resource selection model for data grid based on QoS[J].New Trends and Applications of Computer-Aided Material and Engineering, 2011, 186:203-209. [7] TANG B, ZHANG L.Optimal replica selection algorithm in data grid[J].Theoretical and Mathematical Foundations of Computer Science, 2011, 164:297-304. [8] RAHMAN R M, BARKER K, ALHAJJ R.A predictive technique for replica selection in grid environment[A].Proceedings of the 7th IEEE International Symposium on Cluster Computing and the Grid[C].Rio de Janeiro, Brazil, 2007.163-170. [9] NASEERA S, MADHU MURTHY K V.Performance evaluation of predictive replica selection using neural network approaches[A].Proceedings of 2009 International Conference on Intelligent Agent and Multi-Agent Systems[C].Chennai, India, 2009. [10] RAHMAN R M, ALHAJJ R, BARKER K.Replica selection strategies in data grid[J].Journal of Parallel and Distributed Computing,2008,68(12):1561-1574. [11] ALMUTTAIRI R M, WANKAR R, NEGI A,et al.Replica selection in data grids using preconditioning of decision attributes by K-means clustering (K-RSDG)[A].Proceedings of the 2nd Vaagdevi International Conference on Information Technology for Real World Problems[C].Warangal, India, 2010.18-23. [12] LI J.A replica selection approach based on prediction in data grid[A].Proceedings of the 3rd International Conference on Semantics,Knowledge, and Grid[C].Xi'an, China, 2007.274-277. [13] WU C, Wu K G, CHEN M,et al.Dynamic replica selection services based on state evaluation strategy[A].Proceedings of the 4th ChinaGrid Annual Conference[C].Yantai, China, 2009.116-119. [14] MUNOZ V M, VICENTE G A, CARBALLEIRA F G,et al.Emergent algorithms for replica location and selection in data grid[J].Future Generation Computer Systems-the International Journal of Grid Computing-Theory Methods and Applications, 2010, 26(7):934-946. [15] XIONG R Q, LUO J Z, SONG A B,et al.QoS preference-aware replica selection strategy using mapreduce-based PGA in data grids[A].Proceedings of the 40th International Conference on Parallel Processing[C].2011.394-403. [16] WANG X, DING S F.An overview of quotient space theory[J].Sports Materials, Modelling and Simulation, 2011, 187:326-331.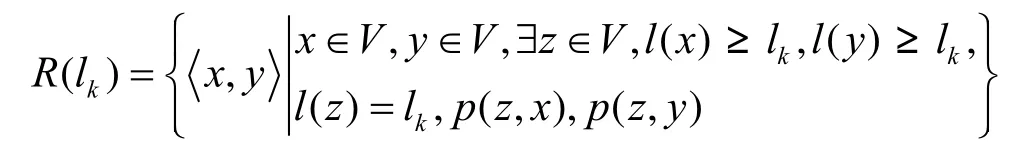


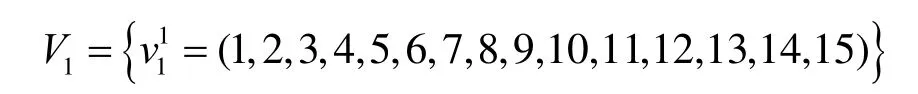
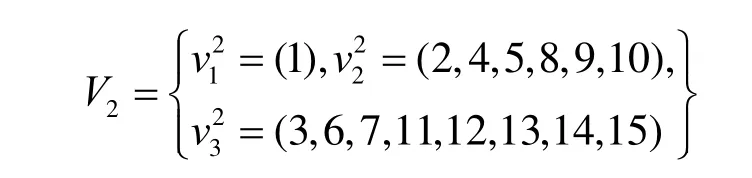
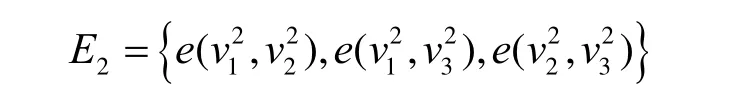
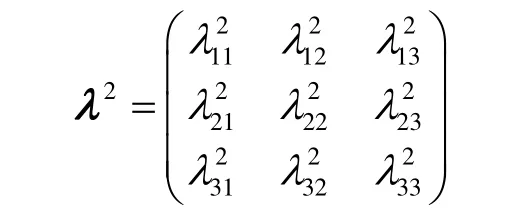
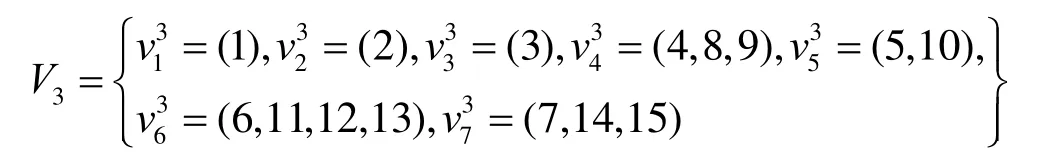

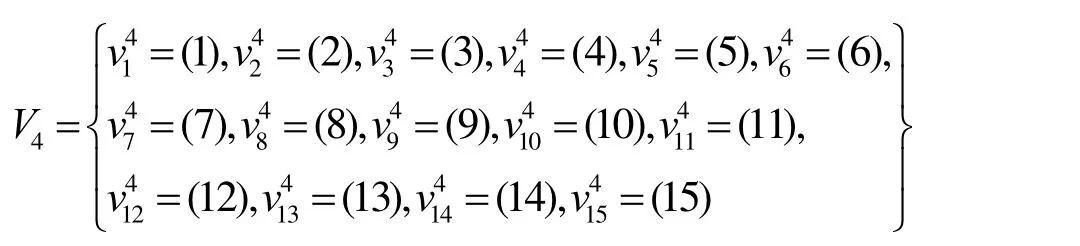
3.3 算法分析
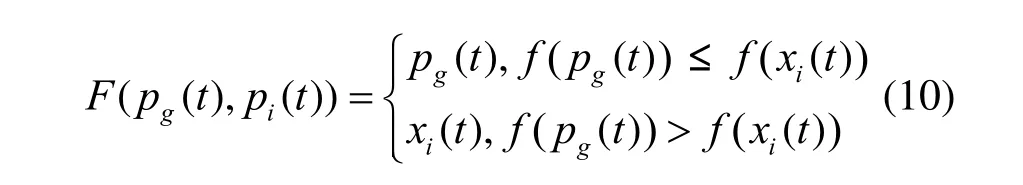
4 仿真实验与分析
4.1 仿真环境与实验方法
4.2 不同QoS级别性能分析
4.3 全局均衡性能分析
4.4 算法收敛速度分析
4.5 与其他算法比较分析

5 结束语
