基于Arnold变换的改进图像加密算法研究

第二炮兵工程学院 四系，西安 710025

第二炮兵工程学院 四系，西安 710025

1 引言

数字图像置乱是将一幅图像经过变换，使其成为面目全非的另一幅没有明显意义的混乱图像。置乱是在信息隐藏中对数字图像所做的预处理，也叫做信息伪装。图像置乱所依赖的信息隐藏技术不仅提供了非密码的安全途径，更引发了信息战尤其是网络情报战的革命，产生了一系列新颖的作战方式，引起了许多国家的重视。网络情报战是信息战的重要组成部分，其核心内容是利用公用网络进行保密数据传送。经过置乱算法加密的图像是混乱无序的，攻击者无从下手来破解这些加密文件。

随着数字水印技术的兴起，置乱技术在通过置乱来分散错误比特的分布从而提高数字水印的鲁棒性方面又有了新的应用。其中Arnold置乱算法简单且具有周期性，所以在数字水印方面得到了很好的应用[1]（Arnold置乱是V.J. Arnold在研究环面上的自同态时提出的，后来把它应用到数字图像上）。Arnold置乱的周期性是一个很好的性质，当反复应用Arnold置乱时，在某一时刻就能恢复原图。因为Arnold置乱的周期性与图像大小有关，可以利用它的周期性来恢复原图，势必要等很长时间。一般图像阶数与Arnold变换的周期并不成正比[2]。

目前，大多数文献资料所举出来的Arnold置乱算法是在正方形数字图像上进行的，这些图像多数是N×N像素的数字图像。然而现实中，多数的数字图像都是非方形的，这样一来就限制了Arnold置乱算法的应用范围[3]。为了弥补这方面的不足，要改进原来的Arnold置乱算法，让Arnold置乱算法应用到M×N像素的非方形数字图像，即该图像的长度和宽度不相等的数字图像[4]。

2 基于Arnold变换的图像置乱

2.1 Arnold置乱算法原理

有单位正方形上的点(x，y)如图1[5]。

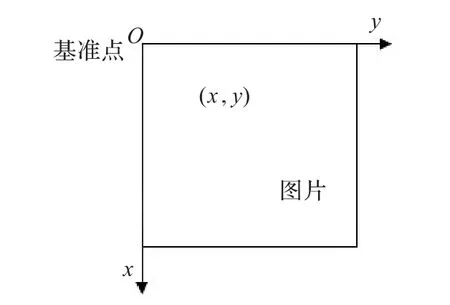
图1 图像坐标分布

将点 (x，y)变到另一点 (x′，y′)的变换为：

此变换称作二维Arnold置乱，具体到数字图像，把式（1）中的二维Arnold置乱改写为：

以后所说的Arnold置乱即式 2。其中，x，y∈{0，1，2，…，N-1}，而N是数字图像矩阵的阶数。记式（2）中的变换矩阵为A，右端 (x，y)T为输入，左端 (x′，y′)T为输出，考虑其反馈，由此可做迭代程序如下：

式中，n代表迭代的次数，n=0，1，2，…。图像信息（如灰度值）伴随离散点阵的置换进行移植，当原图像中所有的点均遍历一遍后，便生成了一幅新的图像[6-7]。

2.2 基于Arnold变换的数字图像置乱

对于数字图像，可以看作一个二维矩阵，图像的阶数即是图像的尺寸若为N，则I有 N×N个元素，下标 x，y表示像素所处的位置，x，y∈{0，1，2，…，N-1}。将 x，y对应于Arnold置乱中的 x，y，对每一对 x，y都做Arnold置乱之后得到 x′，y′，相当于将原图像中的点从 (x，y)移动到 (x′，y′)从而实现了对图像中像素点的移动，用Arnold置乱遍历图像中所有点，就完成了一次图像的Arnold置乱。

Arnold置乱的周期性与图像的大小有关系，但是不成正比。如大小为128×128像素的图像的Arnold置乱的周期为96，大小为240×240像素的图像的Arnold置乱的周期为60。表1给出了不同N值与Arnold置乱的周期T之间的关系。

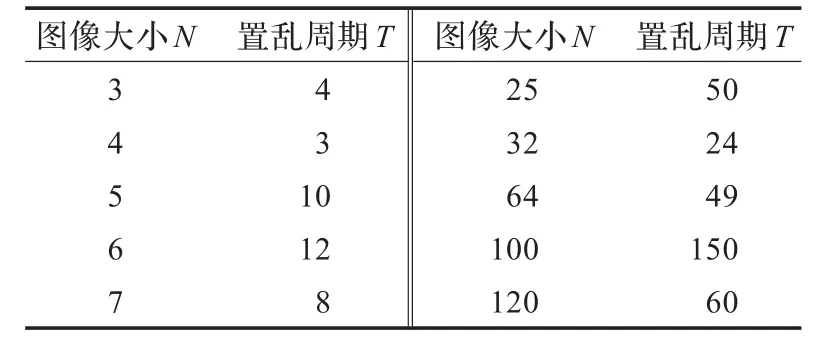
表1 Arnold置乱算法周期

2.3 Arnold置乱算法的置乱恢复

Arnold置乱恢复方法有两种：一种是利用其周期性，另一种是求其逆矩阵的方法从而进行反变换[8]。利用Arnold置乱周期性恢复的方法是很自然的，前面通过研究Arnold置乱的周期性，已经得出了这样的结论：对于N×N像素的数字图像，只要满足N为非1正整数，则Arnold置乱均具有周期。推广到任意置乱次数n，则需要继续进行(mN-nmod mN)次Arnold置乱变换。但是，Arnold置乱的次数与阶数N有关，一般来说，如果是阶数N比较高的情况下，周期也比较长。

另外，在实际应用中，应尽可能地减少Arnold置乱的恢复时间，希望Arnold置乱的周期越短越好，这样就限制了图像的选择，所以，使用求逆矩阵的方法可能效果会更好。比如周期为100次，之前已经置乱了30次，那么，使用逆向置乱的方法，就只需要运行30次，而传统的方法就需要把剩下的70次置乱运行完毕。

两种方法各有优缺点，需要根据置乱的周期和已经置乱的次数选择。

3 一种改进的Arnold算法模型

3.1 改进Arnold置乱算法的基本原理

在一幅非方形数字图像中选择L×L像素区域，进行Arnold变换，从而实现部分区域置乱。图2展示了利用改进的Arnold置乱算法进行图像中单个区域置乱的思路。

部分区域置乱的思想：把选定区域的最左上角像素的坐标 (x1，y1)设定为（1，1），这个区域转换后的坐标为(X-(x1-1)，Y-(y1-1))， 那么原来的 Arnold置乱公式（1）、（2）变换为式（4）、（5）：

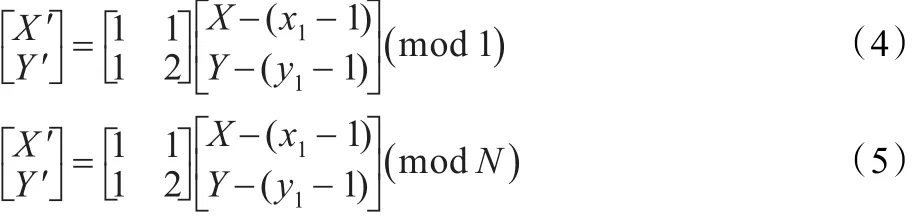
其中(x1，y1)是在一幅图像中任意选择的正方形区域的最左上角的坐标，x，y∈{0 ，1，2，…，N-1} ，而N是数字图像矩阵的阶数。

对于单幅非正方形图像单个区域的Arnold置乱，即在非正方形内随意取一个同大小的正方形区域，所选区域变换的只有基准点的坐标，其运算原理是和Arnold运算是相同的。Arnold置乱算法在这里仍然可用。

对于多个区域的Arnold置乱，其道理就是把图像进行分割成不相等的多个方形区域，每个区域进行Arnold不同次数的置乱。置乱过程是像素点的物理位置变化，在选取区域时可以重叠。加密后的重叠区域出现未加密状况的机率很小，因为两个区域的置乱顺序是有先后的，第一块置乱的区域置乱后，重叠区域的像素点应是第一块区域非重叠区域的像素点，第二块置乱的区域置乱后，又把重叠区域的像素点变换到第二块区域的非重叠区域。

3.2 置乱程度原理

由置乱变换的概念可以看出，位置空间的置乱实质上是原图像像素位置发生了移动，置乱图像的像素相对于原图像的像素移动的距离越远，其置乱程度越大。置乱虽然不改变原图像像素的灰度值，但是可以改变图像的视觉效果。置乱图像相对于原始图像越“乱”，表明该置乱算法越有效。一幅较“乱”的图像应该是直观视觉感到“杂乱无章”，整体灰度分布比较均匀的图像。由前面分析可知，衡量图像置乱程度不仅要考虑图像像素移动的距离，还要考虑图像的直观视觉效果。可用下式的Ds客观地表示图像的置乱程度[9]。

其中DSF（Distance Scrambling Factor）通过计算像素移动距离来确定；GSF（Gray Scrambling Factor）通过量化直观视觉效果来计算。

一般来说，图像像素位置移动得越远，其置乱程度越大，因此可用移动距离来表示其置乱程度。此处采用像素移动距离的均值和方差来计算DSF。

定义 1 假定图像 AM×N，经置乱后变为图像 A′M×N，某像素位置 (x，y)映射为置乱后图像的 (x′，y′)位置，则像素移动距离为：

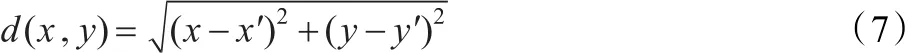
则整幅图像移动距离的均值为：

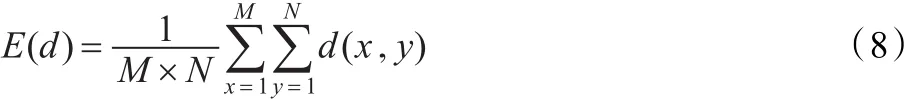
显然，当图像中每个像素都不移动，即图像没有置乱时E(d)为最小值Emin(d)=0；当图像中每个像素都移动对角线距离时E(d)为最大值：

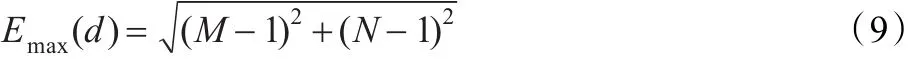
像素移动距离的均值越大表示置乱后像素移动的程度越大，图像置乱的程度越大。故DSF可以用下式计算：

由前面分析可知，若将图像分成大小相同互不重叠的子块，则置乱图像各子块的灰度均值越接近，图像“乱”的程度越大。由此，可用下面的方法计算GSF。

将原始图像和置乱图像分成k×k像素大小的互不重叠子块，设子图像 Bm×n(i，j)表示图像的第(m，n)个子块，则子图像 Bm×n(i，j)的灰度均值 E(Bm×n)为：

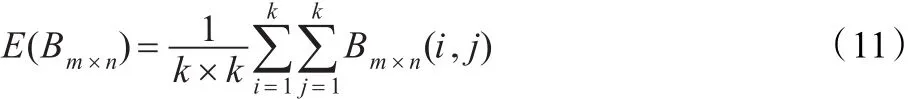
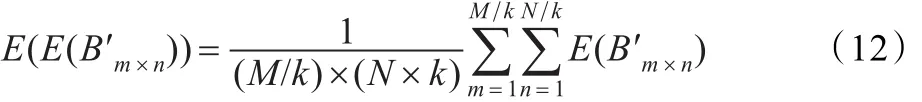
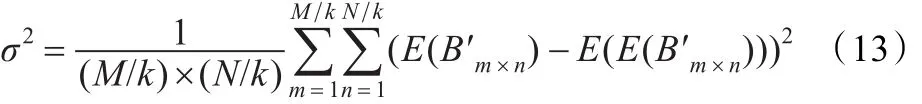
由于方差描述的是随机变量相对于均值的波动程度，方差越小波动程度越小，方差越大，波动程度越大。因此可用子图像灰度均值的方差来描述图像的置乱程度。方差越小，则各块之间灰度均值相差越小，即灰度分布越均匀，即图像“乱”的程度越大。

由上式可见，GSF越大，图像相对于原始图像越“乱”，置乱效果越好。

置乱度Ds值的计算结果还与图像分块有关。图像子块不能太小或太大，例如当子块大小为4×4像素时，数量级约为10－2，子块为8×8像素时为10－1数量级。由于图像置乱程度只与Ds值的相对大小有关。不取决于Ds值的数量级，因此在具体应用中只要对图像的分块尺寸相同，总是可以利用Ds值表示图像的里乱程度，用来评价置乱方法。

4 仿真实验及分析

4.1 多区域图像置乱仿真实验

在Matlab 7.1上，分别对单幅图像的单个区域和不同区域进行了Arnold置乱，如图3所示。

图3 单区域不同次数图像置乱效果图

经过了上面的单个区域置乱得出一幅图像进行多次的部分区域置乱，那么这个区域就会全部被置乱。从而使这幅图像的置乱度更高，安全性也就越高。图3（d）所示是由Arnold置乱的周期性恢复得到的原始图像。

两个区域或者多个区域的置乱与一个区域的置乱类似。图像分割如图4（a）：把564×642像素图像总共分成如下6个部分：红色线条：396×396；绿色线条：342×342；蓝色线条：342×342；白色线条：360×360；黄色线条：564×564；褐色线条：564×564。存在重叠区域。图4为对Matlab 7.1环境下，对多区域置乱的实验结果分析。

通过单幅图像多个区域Arnold置乱，置乱后的图像从主观视觉上看不出分割区域的分界线，更找不到隐藏在内部的分割区域的分界线。这样就达到了让非法攻击者无从下手的目的。

图4 多区域置乱效果图

4.2 攻击实验

为了验证加密图像在传输过程中受到攻击时是否有数据丢失，进行如下两种攻击实验。

4.2.1 部分区域剪切实验

利用Photoshop CS4.0软件把置乱后的图像部分区域剪切处理，如图5。

图5 置乱后图像部分区域剪切图

通过恢复程序恢复出来的图像如图6。

图6 部分区域剪切后恢复的图像

经过图像部分区域剪切攻击实验得出：图像虽然经过了部分区域剪切的处理，但是经过图像恢复，所得图像与原图像比较接近。

4.2.2 加入噪声实验

原来的图像加入椒盐噪声处理如图7。

利用Matlab 7.1软件把置乱后的图像加入椒盐噪声处理并恢复如图8。

经过噪声攻击实验得出：置乱的数字图像受到噪声攻击后，恢复得到的图像，和原图像受到噪声攻击的图像几乎是一样的。说明这种置乱算法抗噪声攻击比较弱。

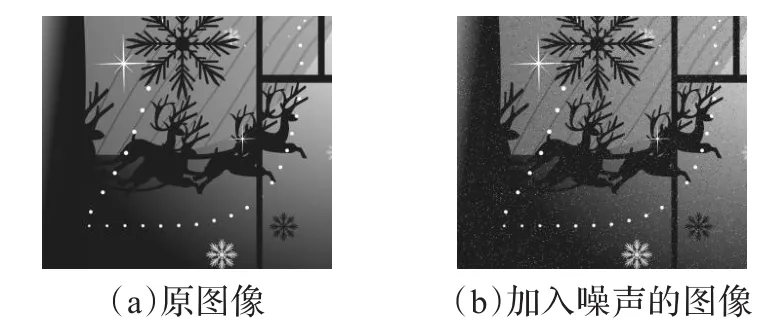
图7 原图像和加入噪声的图像

图8 置乱后图像加入噪声和恢复

4.2.3 进行多次置乱攻击对比

对原图像分别进行6、12、18个区域的置乱，如图9。

图9 原图不同区域个数置乱

分别对6次、12次、18次置乱的图像进行剪切部分区域攻击，并且进行恢复。剪切区域大小为250×250像素，如图10。

图10 不同次数置乱的图像被剪切并恢复

通过以上三种攻击性实验得出结论：Arnold置乱算法在置乱图像部分区域剪切后，进行恢复时，能基本还原初始图像。置乱图像在噪声攻击后，进行恢复得到的图像与原来图像受到噪声攻击时几乎一样，说明Arnold置乱算法与噪声攻击之间不会相互影响，图像即使被噪声攻击之后，仍然可以用该算法对图像进行恢复性处理。

5 结束语

本文研究了图像置乱算法，并通过图像置乱来给图像加密，提高图像的安全性。在传统Arnold置乱算法中，都是对方形图像进行置乱，本文提出的多区域置乱方法不仅可以用于方形图像，更适用于任何非方形图像，通过多区域的置乱，更能有效提高图像的安全性，使破译难度难上加难，并通过Matlab 7.1下的仿真实验，验证了这一点。实验数据表明，该改进后的算法是切实可行的。

[1]Delaigl E J F，Vleeschouwer C D，Macq B.Watermarking algorithm based on a human visual model[J].Signal Processing，1998，66（5）：319-336.

[2]Swanson M D，Zu B，Tewfik A H.Robust data hiding for images[C]//Proc IEEE 7th Digital Signal Processing Workshop（DSP 96），1996，9：37-40.

[3]贾松浩，杨彩，张海玉，等.一种改进的Arnold变换[J].河南大学学报：自然科学版，2009（2）：199-202.

[4]QiDongxu，Zou Jiachun，HanXiaoyou.A new classof scrambling transformation and its application in the image information covering[J].Sciencein ChinaScrics，2000，43（3）：304-312.

[5]Baraff D，Witkin A，Kass M.Untangling cloth[J].ACM Transactions on Graphics，2003，22（3）：862-870.

[6]王璐璐，张翀.基于Arnold置乱的数字图像加密技术研究[J].国防技术基础，2010（10）：38-42.

[7]黄仿元.基于Arnold置乱的图像置乱算法及实现[J].贵州大学学报：自然科学版，2008，25（3）：276-279.

[8]吴玲玲，张建伟，葛琪.Arnold变换及其逆变换[J].微计算机信息，2010（14）：206-208.

[9]黄良永，肖德贵.二值图像Arnold变换的最佳置乱度[J].计算机应用，2009（2）：474-483.

基于Arnold变换的改进图像加密算法研究

梁 婷，李 敏，何玉杰，黄克宇

LIANG Ting,LI Min,HE Yujie,HUANG Keyu

Department of 4th,Second Artillery Engineering University,Xi’an 710025,China

With the development of information security,the traditional scrambling algorithm based on Arnold transformation is only applied to the square area,which is a big limitation.It has been far from to ensure the security of images in the transmission process.This paper presents a new image encryption algorithm,which can improve the security of image during transmission more effectively.Focus on this,a multi-region algorithm for image scrambling encryption model is proposed,which splits the non-square image to multiple square regions,and scrambles each region.Experimental results show that the new algorithm improves the image security effectively to avoid decipher,and it also can restore the image almost as same as the original image, which reaches to the purposes of image safe and reliable transmission.

image scrambling;Arnold transformation;multi-regional;scrambling degree;image encryption

随着现在图像破译技术的提高，传统的基于Arnold变换的置乱算法仅适用于正方形区域，存在很大的局限性，已经远远不能保证图片在传送过程中的安全性了。提出了一种新的多区域置乱算法的图像加密模型，即对于非正方形图像采用划分多区域，分别对每个区域进行置乱的思想。实验数据显示，新算法不仅有效地提高了图像的安全性，使破译起来无从下手，而且对置乱后的图像恢复，与原图几乎是一样的，达到了图像安全、可靠传输的目的。

图像置乱；Arnold变换；多区域；置乱程度；图像加密

A

TP391

10.3778/j.issn.1002-8331.1110-0100

LIANG Ting,LI Min,HE Yujie,et al.Method of improved image scrambling based on Arnold transform.Computer Engineering and Applications,2013,49（11）：204-207.

梁婷（1989—），女，硕士研究生，主要研究方向为信息安全；李敏（1971—），女，博士后，教授，博导，主要研究领域为智能图像信息处理。E-mail：lt_aries@126.com

2011-10-09

2011-12-09

1002-8331（2013）11-0204-04

CNKI出版日期：2012-03-08 http://www.cnki.net/kcms/detail/11.2127.TP.20120308.1520.022.html

◎工程与应用◎