一种新的数据流在线压缩存储方法

北京林业大学 信息学院，北京 100083

北京林业大学 信息学院，北京 100083

1 引言

数据流数据的处理近年来得到越来越广泛的重视，其原因在于，随着网络技术的发展，在电子商务，网络监控，证券股票、无线通信网等等，数据流成为一种较为普遍的信息传送方式。数据流是一组顺序、大量、快速、连续到达的数据序列，是一种特殊的数据类型。由于数据流是连续到达且具有无限性，有限的处理机不可能保存数据的全部信息。另一方面，对于某些系统，比如对于设备或场景监控的应用，这类数据往往呈现多点并发，流量巨大等特点，而且数据流的信息中往往含有大量的冗余，可能大多数情况下时间序列中的数据是有很强的关联性的，甚至是相等的[1]。在保证数据精度的情况下，采用正确的方法对数据流进行描述，不仅是发现数据关联的有效途径，对于压缩数据量，减少系统存储压力，加快数据查询速度，也具有重要的意义。

目前，对于流数据处理普遍的做法是在存储器中开辟一个滑动窗口来保存近期到达的数据流数据，以实时地支持查询请求。随着数据流不断地流入滑动窗口，当滑动窗口数据已满时，将会有部分旧数据从滑动窗口中流出。流出滑动窗口的这部分数据称为历史数据。基于数据流历史数据的压缩处理算法已经有了一些研究结果。这些研究方法都是基于抽样的，但是在很多情况下，常常需要保存连续的数据[2]。因此，抽样的方法并不能满足这种需求。

工业上处理数据流的压缩算法主要有旋转门压缩算法和死区限值压缩算法。旋转门压缩算法是美国OSI软件公司开发的PI实时数据库系统（Plant Information System）采用的专利压缩技术。旋转门压缩算法保存的是实际的数据，因此，要获得数据的趋势还必须经过二次处理才能得到。其次，旋转门压缩算法摒弃了一些数据，当这些数据需要恢复时，可能会遇到困难。死区限制压缩算法仅仅保留大于死区限值的值，小于死区限值的值将会被舍弃，因此数据精度得不到保证。

针对以上算法的缺点，本文采用加权分段曲线拟合的方式对数据流历史数据进行压缩处理，同时采用k-means聚类算法对拟合结果进行聚类处理，找出数据的规律，并根据聚类的结果采用选择合适窗口进行数据处理。这样既实现了数据的压缩处理，又可以随时恢复压缩的数据，并且拟合的结果可以作数据流的函数表达式，具有良好的优点。本文最后通过实验，分别对加权分段曲线拟合算法的拟合精度，压缩率和实用性进行了测试，证明了算法的有效性。

2 加权最小二乘法曲线拟合

数据流是一组顺序、大量、快速、连续到达的数据序列，与时间密切相关。可以将数据流视为无限多重集合，集合中每个元素具有形式，其中s是一个元组，t为标识s的时间戳，t的取值可以是s进入数据流系统的时间或者数据源产生s的时间。将元组中的一维数据与时间取出来单独考虑，则数据流是一个关于时间t的函数。因此可以采用曲线拟合的方法对数据流进行处理。

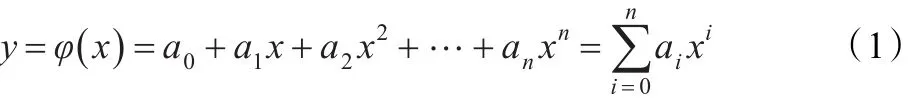
的求解方法。则根据不同的定义方法，则可能求解出无数条拟合曲线。对于求解出来的拟合曲线，并不要求其经过实验数据中的每个数据点，而是希望曲线 y=φ(x)尽可能地靠近数据点，并且靠近的个数最多。设根据φ(x)算出第i点的函数值与实际值的误差为εi：

最小二乘法曲线拟合是以“方差最小”为判断依据的曲线拟合方法，即

为最小。

在实际的应用中，并不是所有数据点的重要性都一样，特别是曲线有突变的情况下，此时突变点的数据就显得很重要。所以应对不同的数据点赋予不同的权值，重要的数据点赋予较大的权值，一般的数据点则赋予较小的权值。这种带有权值的最小二乘法曲线拟合就是加权最小二乘法曲线拟合。加权最小二乘法曲线拟合函数是关于x的n次多项式：

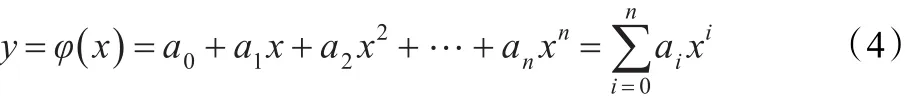
它的系数可通过求解正规方程组得到。设权值为w，则相应的正规方程组为：

对于曲线拟合来说，除了要获得拟合结果外，还需要对曲线拟合的结果进行精度的控制，即εi不能太大。根据文献[3]，知道对于曲线拟合的精度与以下三个方面有关：分段拟合的段数、曲线拟合的阶数以及数据点权值的分布。因此，为了获得良好的精度，应当采用综合各个因数进行分段拟合的方式。拟合的段数越多，在同一段中采用的拟合阶数越高，段中数据点的权值分布越合理，则拟合精度越高。变阶加权分段方式可以自动获取最合适的数据点对数据流进行分段，并对分段后的数据采用合适的阶数进行拟合，具有良好的性能。因此，本文采用变阶加权分段方式对数据进行最小二乘曲线拟合，以提高曲线拟合的精度。

在曲线拟合的过程中，拟合窗口选择越大，则数据处理的时间越长，拟合精度也会下降。但如果窗口选择的长度过短则不能有效地把握数据流的趋势。所以，采用合适的窗口大小可以降低数据处理的时间，其次可以根据数据的特点采用合适的分段对数据进行拟合，提高了数据拟合的精度。文献[4]介绍了一种结合两种方式的特点的窗口选择方案，具有较好的性能。因此本文的窗口设置采用这种方式，即设定一个标准的数据窗口作为拟合处理的最小长度，同时设置一个较大的数据窗口作为拟合处理的极限长度。处理的过程如下：

（1）接受数据的流入，当数据的长度大于标准长度时，对数据进行曲线拟合，并求出拟合的最大误差。

（2）若最大误差小于设定的最大误差限，则继续接受数据，重复（1）步骤。否则，以最大误差点作为数据分段点，对分段点前的数据拟合，将拟合结果保存；对分段点后的数据作为新的处理起点。

（3）当数据的长度大于极限长度时，对数据拟合，并将拟合结果保存，同时将下次读入的数据作为新的处理起点，重复（1）步骤。

3 k-means聚类算法

聚类是一种将给定数据集按照一定的方式划分成若干组或若干类的过程，使得同一类中的数据具有较高的相似性，而不同类的数据的相似性较低。采用聚类算法可以发现数据间内在的规律，为数据处理提供决策依据[5]。本文采用k-means聚类算法对拟合的结果进行聚类分析，获得数据的内在规律。

k-means聚类算法的处理思路是给定一个数据样本，用户输入要获得聚类簇的个数k，将数据划分为k个部分，然后通过更新簇的中心来调整划分，当整体差异函数收敛的时候结束处理过程。聚类之间的差别是簇中心的表示方法，划分调整策略和整体差异函数的定义。k-means聚类算法的处理流程如下：

（1）在样本中任意选择k个数据作为初始聚类中心。

（2）计算每个数据到这些聚类中心的距离，并根据最小距离对数据进行重新划分。

（3）重新计算每个聚类的中心。

（4）循环第（2），（3）步直至聚类不再发生变化。

本文采用k-means聚类算法的目的是寻找数据流的规律，即通过对曲线拟合结果进行聚类，找出数据的周期。由于k-means聚类算法需要预先给定聚类的个数k并且对初值较为敏感，而对于数据流来说，并不知道给定的数据集划分成几个类别才合适，因此本文对k-means聚类算法作了一下改进，来满足数据流的需要。具体做法是通过设定合适的初始距离来设定初始聚类中心，处理流程如下：

（1）设定初始距离。

（2）计算新数据到每个聚类中心的距离，若最小距离大于初始距离，则新数据为新聚类的中心，否则根据最小距离对数据进行划分。

（3）重新计算每个聚类的中心。

（4）循环第（2），（3）步直至聚类不再发生变化。

（5）循环第（2）～（4）步直至数据全部处理完。

聚类算法处理需要大量的数据，所以，可以将数据缓存一段时间，待数据足够多时，才采用算法进行处理。数据到聚类中心的距离为数据到聚类均值的欧氏距离。

4 原型实现

为了将数据流历史数据合理地压缩，同时最大限度地保留数据流的所有信息，本文通过实验，找到了比较合理的算法：分段加权曲线拟合算法。首先采用加权分段曲线拟合算法对流数据进行拟合处理。同时采用k-means聚类算法对处理结果进行聚类分析，找出数据流的规律。若数据流是有规律的，则通过求出数据流的周期，然后采用合适的长度对数据进行拟合，并保存拟合结果。若数据流是没有规律的，则加权分段曲线拟合处理结果也可以直接保存。

本文采用的方法如下：

（1）接受数据，采用加权分段曲线拟合算法对数据进行曲线拟合。

（2）当拟合结束时，求出最大拟合误差。

（3）若最大拟合误差大于阈值，则最大误差数据的权值加1；否则，继续接受数据进行拟合。

（4）若权值大于或等于最大权值，则将拟合阶数加1；若拟合阶数大于最大拟合阶数，则以最大误差点作为分段点。

（5）对分段的数据采用合适的阶数进行曲线拟合，并将拟合结果保存。

（6）若临时表中的数据大于最大个数，则将临时表的数据进行曲线拟合，并将拟合结果保存。

（7）当拟合的结果足够多时，采用k-means聚类算法对拟合结果中的参数进行聚类分析。

（8）若聚类分析结束后，聚类结果稳定，则采用合适的长度对数据拟合，保存拟合结果。

下面给出了主要算法的描述，以下将以伪代码的形式对本文的方法进行描述。具体伪代码如下：

本文用聚类算法对拟合结果进行分析处理，主要是根据拟合的结果找出数据的规律，即找出数据的周期。假如数据是有周期的，则可以求出最佳的数据长度。将最佳数据长度设置为拟合窗口的长度，对数据进行拟合处理，得出的拟合结果，然后根据拟合结果对数据进行处理。

5 实验及分析

为验证文中方法的有效性，本文搭建了一个测试平台对文中的方法进行了测试。测试平台的硬件环境为Pentium®4 CPU 3.00 GHz 2.00 GB内存，软件环境为Window XP下的Microsoft Visual Studio 2005及Microsoft SQL Server 2005。实验数据集为采集的一类地理信息数据。

实验1算法拟合精度验证。采用变阶加权分段曲线拟合算法对样本数据进行测试。读取的样本数据为34个，最大误差限设置为0.001，标准窗口大小设置为10，最大数据窗口大小设置为20，最大权值设为10，最大拟合阶数设为3。拟合结果共分为4段，其中三阶多项式的为3段，二阶多项式的为1段，具体结果如下：

曲线拟合结果和原始数据的对比图如图1所示。

利用拟合后得到的结果，将原始数据还原。将还原的数据与原始数据对比，对比图如图1所示。从拟合结果上看，大部分数据都得到了很好的拟合，少部分数据出现了一些误差，最大误差出现在第26点，误差为0.000 904 2，小于最大误差限。对于数据流来说，已满足数据处理精度的要求。

实验2算法的压缩效率验证。本实验采用的测试样本数据大小为48.5 kb，分别采用加权分段曲线拟合压缩算法和旋转门压缩算法对测试样本进行压缩，算法的数据精度设定为0.003。其中，旋转门压缩算法的存储字段为序号（No），系统编号（SystemId），时间（Time），数据值（Data）。加权分段曲线拟合压缩算法的参数设置为，最大权值为5，最大阶数为4，标准窗口设置为15，最大窗口设置为20。存储的字段为序号（No），系统编号（SystemId），开始时间（StartTime），参数 1（A0），参数2（A1），参数3（A2），参数4（A3），参数5（A4），拟合个数（Num）。压缩结果如表1所示。

表1 两种算法压缩对比

从处理结果上看，采用合适的阶数，合适的窗口大小，在同样的压缩精度下，加权分段曲线拟合压缩算法压缩率要比旋转门压缩算法高。由于本文方法的参数存储较多，所以，在复杂变化，规模较大的数据描述中，才能更加体现优势。

实验3对有一定周期性数据的处理。采用的样本数据具有一定的周期性，大小为22.8 kb。样本数据的散点图如图2所示。旋转门压缩算法的存储字段为序号（No），系统编号（SystemId），时间（Time），数据值（Data）。本文算法的参数设置为：最大权值为10，最大阶数为4，标准窗口设置为20，最大窗口设置为30。存储的字段为序号（No），系统编号（SystemId），开始时间（StartTime），参数1（A0），参数 2（A1），参数 3（A2），参数4（A3），参数5（A4），拟合个数（Num）。

图1 曲线拟合对比图

图2 聚类数据源散点图

加权分段曲线拟合后数据共分为20段，聚类的初始距离设为0.003，聚类结果共分为2类，每类的段数为：10，10。通过计算得到数据的周期为40。压缩数据精度设置为0.003，分别采用旋转门压缩算法，不考虑聚类时的本文算法及考虑聚类时的本文方法对数据压缩处理，处理结果如表2所示。从处理结果上看，考虑聚类时本文方法的压缩率要比旋转门压缩算法及不考虑聚类时本文算法的压缩率要高。

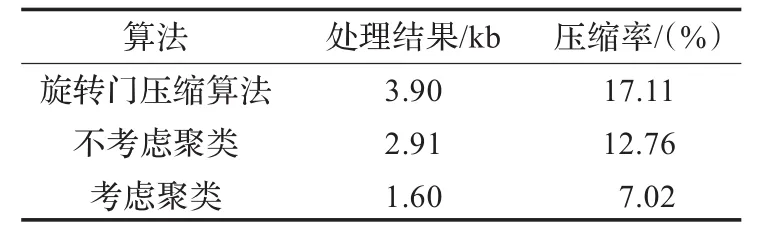
表2 3种不同方法压缩率比较

6 结论

本文提出了一种新的存储数据流的处理方法。通过实验1，采用变阶加权分段曲线拟合算法对拟合精度进行了验证。实验2通过对比采用加权分段曲线拟合压缩算法和旋转门压缩算法来验证了本文算法的压缩效率。实验3中加入了周期数据的因素，考虑到了聚类，并对测试数据进行实验对比，得出聚类对周期数据压缩效率有所提高的结论。综上，从实验结果来看，通过设置合适的参数，在同样的压缩精度下，加权分段最小二乘算法曲线拟合具有很好的拟合精度及压缩率。若同时采用k-means聚类算法，并且处理的数据是周期性时，数据压缩效果将会更加显著。由于存储的是数据流的曲线拟合结果，所以可以获得数据流的规律，解决了抽样方法不能有效获得数据流规律的问题。通过采用加权最小二乘法对缓存数据流进行分段曲线拟合，并结合聚类算法进行分析处理，可以很好地实现数据的压缩存储。

本文提出的方法具有较好的可行性。在现实处理中，数据流的数据可能是周期性的，也可能是非周期性的。对于周期性的数据，本文方法只存储少量的数据，与实际相符。对于非周期的数据，本文方法拟合的结果可以直接作为压缩结果保存，避免了再次压缩处理。但本文也有不足的地方，如方法只能拟合一维数据；曲线拟合的阶数，窗口大小等参数需要设置恰当，才能得到较好的压缩率；聚类算法中的初始距离需要人为设定，对于不熟悉数据特性的人员来说，聚类的结果可能得不到理想的数据。这些也是本文以后需要努力改进的地方。

[1]Saito T，Kida T，Arimura H.An efficient algorithm for complex pattern matching over continuous data streams based on bit-parallel method[C]//IEEE International Workshop on Databases for Next Generation Researchers.[S.l.]：IEEE Press，2007：13-18.

[2]Parpinelli R S.Data mining with an ant colony optimization algorithm[J].IEEE Transactions on Evolutionary Computation，2002，6（4）：321-322.

[3]Bristol E H.Swinging door trending：adaptive trend recording[C]// ISA National Conference Proceedings，1990：749-754.

[4]Araru A，Babu S，Widom J.An abstract semantics and concrete language for continuous queries over and relations[EB/OL]. [2011-04-12].http：//dbpubs.Stanford.edu/pub/2002-57.

[5]Kang J，Naughton J，Viglas S.Evaluating window joins over unbounded stream[C]//The 19th Int’l Conf on Data Engineering，Bangalore，India，2003.

[6]Golab L，Ozsu M T.Processing sliding window multi-joins in continuous queries overdata streams，Tech Rep：CS-2003-01[R].[S.l.]：Waterloo University，2003.

[7]Zhu Y，Shasha D.StatStream：statistical monitoring of thousands of data streams in real time[C]//The 28th Int’l Conf on Very Large Data Bases.Hong Kong：[s.n.]，2002.

[8]Datar M，Gionis A，Indyk P，et al.Maintaining stream statistics over sliding windows[C]//The 13th Annual ACM SIAM Symp on DiscreteAlgorithms，San Francisco，California，2002.

[9]Ziv J，Lempel A.A universal algorithm for sequential data compression[J].IEEE Transactionson Information Theory，1977，23（3）：337-343.

一种新的数据流在线压缩存储方法

冯秀兰，张 帆

FENG Xiulan,ZHANG Fan

School of Infomation Science and Technology,Beijing Forestry University,Beijing 100083,China

The sampling storage method which is used in the current data stream ignores the historical data for the analysis of data stream processing and storage management issues.For the problem,this paper presents a new processing method based on curve fitting.A weighted least-square principle is used to fit the cached stream data and better model description is obtained.The fitting results are analyzed by clustering algorithm,which serves as a classifier for polynomial fitting parameters.According to the clustering result,the appropriate window size will be given to fit the periodic stream data.Comparing the forecast result with the actual data,different methods are adopted to store data according to the comparison result.The experimental results indicate that the proposed method has good performance,can meet different processing requirements.

curve fitting;data stream;clustering algorithm;least-square principle

针对当前数据流采用的抽样存储方法忽略了对数据流历史数据的分析处理与存储管理的问题，提出一种新的存储数据流的方法。在满足数据精度的情况下，采用加权最小二乘法对缓存数据流进行分段曲线拟合，对拟合结果进行聚类分析。根据聚类分析结果，采用合适的窗口对数据进行分段曲线拟合，利用拟合结果预测数据流的趋势。将预测结果与实际数据比较，根据比较结果采用不同的方法存储。实验结果表明，提出的方法具有良好的性能，能够满足不同的处理需求。

曲线拟合；数据流；聚类算法；最小二乘法

A

TP311

10.3778/j.issn.1002-8331.1109-0269

FENG Xiulan,ZHANG Fan.New method for data streams compress and storage online.Computer Engineering and Applications,2013,49（11）：140-144.

冯秀兰（1955—），女，副教授，主要研究方向为数据流挖掘、计算机网络；张帆（1986—），男，硕士，主要研究方向为数据流挖掘。E-mail：zhangfan0755@163.com

2011-09-14

2011-11-08

1002-8331（2013）11-0140-05

CNKI出版日期：2012-01-16 http://www.cnki.net/kcms/detail/11.2127.TP.20120116.0927.042.html

◎图形图像处理◎