基于核主成分分析的数据流降维研究

五邑大学 计算机学院，广东 江门 529020

五邑大学 计算机学院，广东 江门 529020

随着科学技术的发展，人们不断接触到各种类型的数据，如图像数据、文本数据、医学信息数据、金融市场交易数据、天文数据等，大多数情况下这些数据具有多维空间属性，在统计处理中称之为“高维数据”，且具有数据流（Data Stream）性质。数据的高维度和流的形式给数据处理带来巨大的挑战，例如，当处理256×256的图片序列时，通常将图像数据拉成一个向量，这样，得到一系列4 096维的数据序列，如果直接对这些数据进行处理，巨大的计算量将使人们无法忍受，即“数据维灾”，同时这些数据通常没有反映出数据的本质特征，如果直接对它们进行处理，不会得到理想的结果。所以需要对数据进行降维，将数据的维数降到合适大小，同时尽可能多地保留原数据信息，然后对降维后的数据进行处理[1]。

降维是将高维模式映射到低维子空间的过程，其主要目的有：

（1）压缩数据以减少存储量；

（2）去除噪声的影响；

（3）从数据中提取特征以便于进行分类或聚类；

（4）将数据投影到低维空间，便于理解数据分布。

本文讨论了高维数据降维的定义及常用算法，接着对核主成分分析（KPCA）进行研究，并提出一种计算效率更高的分组核主成分分析（GKPCA）算法，实验数据表明，该算法能有效地对数据流进行特征提取，实现高维数据降维。

1 降维的定义及算法

1.1 降维的定义

（1）高维数据空间，ΩD，通常为RD的某一个子集。

（2）降维空间（或称低维表示空间），Ωd。

（3）映射函数φ称 y为x的降维表示。

1.2 降维算法

目前，数据降维方法主要分为两类[3]：线性降维和非线性降维。

线性降维包括：主成分分析（Principle Component Analysis，PCA）、独立成分分析（Indispensable Component Analysis，ICA）、线性判别分析（Linear Discriminate Analysis，LDA）、投影寻踪（Projection Pursuit，PP）等；PCA是一种基于二阶统计的数据分析方法，该方法在各个变量之间相关系研究的基础上，用一组较少的、互不相关的新变量代替原来较多的变量，而且使这些新变量尽可能多地保留原来复杂变量所反映的信息，具体计算步骤可参看文献[4]。

非线性降维算法包括：核方法、多维尺度方法（Multidimensional Scaling，MDS）、等距离映射算法（ISOMAP）、局部线性嵌入（Locally Linear Embedding，LLE）[5]等。

核主成分分析作为PCA方法的在处理非线性问题时的扩展，近年来得到了快速的发展，其主要思想是通过某种事先选择的非线性映射函数将输入矢量映射到一个高维线性特征空间，然后在特征空间中使用PCA方法计算主成分[6]。在具备了PCA所有数学特性的前提下，KPCA还有如下特征：KPCA比PCA提供更优的识别性；KPCA的计算复杂度不因变换空间的维数增加而加大，仅与输入空间的维数相关。目前KPCA的思想已经被世界上广大的科研人员所接受，广泛应用到特征提取、人脸识别[7]、图像识别[8]、光谱降维分析[9-10]、数据分类聚类以及故障监控诊断等领域。

由于KPCA的计算复杂度是和样本数密切相关的，对于一个 N×N的核矩阵（N为样本数），其时间复杂度为O(N3)，当N很大时，KPCA的计算代价会快速增长，因此需要对KPCA算法进行优化，文献[11]介绍了一种将求解PCA的期望最大算法（EM）推广到求解KPCA，但该算法占用存储空间较大，且收敛性不能保证。下面将着重介绍核主成分分析方法与在此基础上的改进算法。

2 核方法与基于KPCA降维算法的改进

2.1 核方法

核方法一种由线性到非线性之间的桥梁，起源于20世纪初叶，是一系列先进性数据处理技术的总称，共同点是这些方法中都用到了核映射。核函数方法的基本原理是通过非线性函数把输入空间映射到高维空间，在特征空间中进行数据处理，其关键在于通过引入核函数，把非线性变换后的特征空间内积运算转换为原始空间的核函数计算，从而简化了计算量。其操作过程如图1所示。

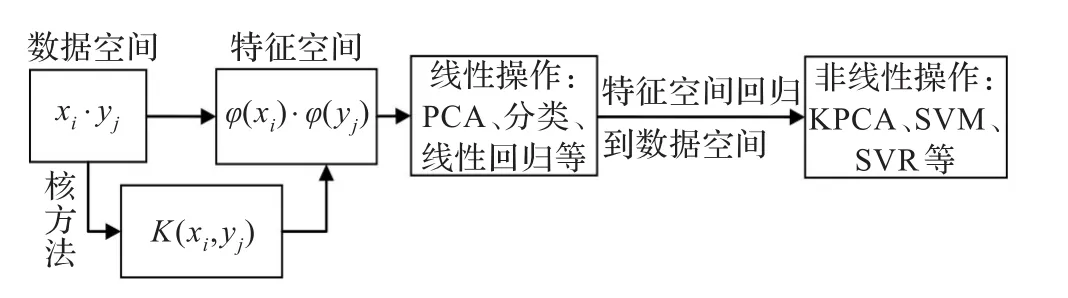
图1 核方法框架示意图

实质上，核方法实现了数据空间、特征空间、类别空间之间的非线性变换。图1中，xi和xj为数据空间中的样本点，数据空间到特征空间的映射函数为φ，核函数的基础是实现向量的内积变换：

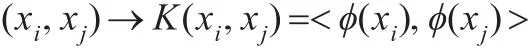
在满足Mercer条件[12]下，设输入空间的数据为 xi∈(i=1，2，…，N)，对于任意对称连续的函数 K(xi，xj)，存在一个Hilbert空间，对映射φ:→H ，有：

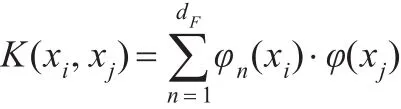
其中dF为H的空间维数。这进一步说明，输入空间的核函数实际上与特征空间的内积是等价的，由于在核方法的各种实际应用中，只需要应用特征空间的内积，而不需要了解具体映射φ的具体形式，即：在使用核方法时只需要考虑如何选定一个合适的核函数，无需关心与之对应的映射φ是否具有复杂的表达式。具体核函数的性质及其构造方法可参看文献[13]。

2.2 KPCA基本原理

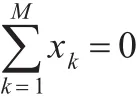
对于经典的PCA算法，通过求解特征方程 λν=Cν，λ为C的一个特征值，ν为相应的特征向量，以此来获得贡献率较大的特征值和与之对应的特征向量。现引入非线性映射函数φ，使输入空间中样本点 x1，x2，…，xM变换为特征空间中的样本点 φ(x1)，φ(x2)，…，φ(xM)，假设：

则在特征空间F中，其协方差矩阵为：

因此，特征空间F的特征值和特征向量求解即求解方程：

从而有：

特征向量ν可以线性表示为：

由式（3）（5）（6）得：

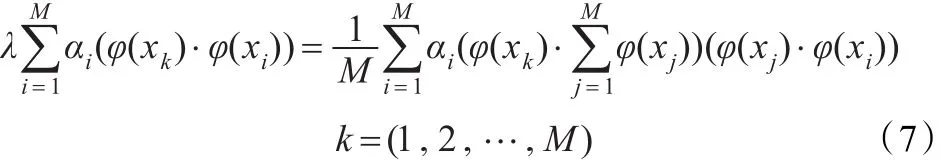
定义M×M的矩阵K：

则式（7）可转化为：

求解式（9）即可获得映射空间上的特征值和特征向量。测试样本在F空间向量Vk上的投影为：

如果特征空间中数据不满足中心化条件，则需要对和矩阵进行修正，用下式中的K代替式（9）中的K：

式（11）中，对于所有的 i，j，li，j=1[14]。

2.3 KPCA实现步骤

（1）从数据流中获取m条数据记录（每条记录有n个属性），将其表示成m×n维的矩阵：

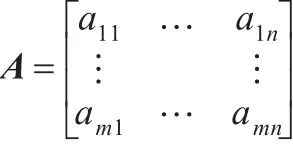
（2）选取适当的核函数，计算核矩阵K，本文中选取高斯径向基（RBF）核函数：

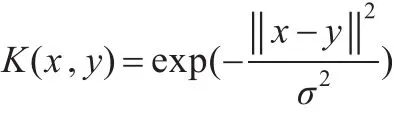
（3）修正核矩阵 K，得 KL。

（4）计算 KL 的特征值 λ1，λ2，…，λn和特征向量 ν1，ν2，…，νn。

（5）将特征值按降序排列，并调整与其对应的特征向量。

（6）利用Gram-Schmidt正交法单位化特征向量，得到α1，α2，…，αn。

（7）计算特征值的累积贡献率 B1，B2，…，Bn，根据给定的提取效率 p，如果 Bt≥p，则提取 t个主分量 α1，α2，…，αt。

（8）计算已修正的核矩阵KL，在提取出的特征向量上的投影Y=KL·α ，其中 α=(α1，α2，…，αt)；所得的投影Y 即为数据经KPCA降维后所得数据。

2.4 GKPCA算法的提出

由于KPCA是基于样本的，算法的时间复杂度和空间复杂度与数据流维数无关，但是与样本记录数目却密切相关，对于小型高维数据流，KPCA能够很好地完成降维，随着样本记录数目的增多，KPCA的时间复杂度和空间复杂度也会增加。

为了降低计算时间与内存消耗，提出一种分组的KPCA算法，即将原始样本先分成若干组，对每一组数据进行过滤，然后再运用KPCA算法。

设原始样本记录数为N，现将其分为G组，则每组记录数目为：

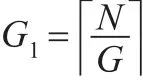
第i(i=1，2，…，G)组中与第一投影方向相对应的系数向量为αi：

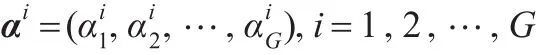
对每一组进行数据过滤，设过滤阈值为ζ，αi按降序排列，设排序后为 β，β满足：β1≥β2≥…≥βG，经过数据过滤后，设保留下来的记录数目为 Lefti(i=1，2，…，G)，则Lefti由下式决定：

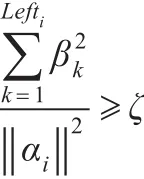
ζ越大，过滤掉的样本记录越少，否则越多。这样，每组数据过滤后形成新的样本集，并对新样本集进行KPCA算法，形成最终的投影方向。GKPCA算法的实现步骤为：

（1）重新采样并进行分组，形成G组样本。

（2）对每一组执行KPCA，并对样本进行过滤。

（3）组合过滤后的样本，形成新的样本数据集，并再次执行KPCA算法，对样本进一步过滤。

（4）获得GKPCA的特征投影。

3 实验与分析

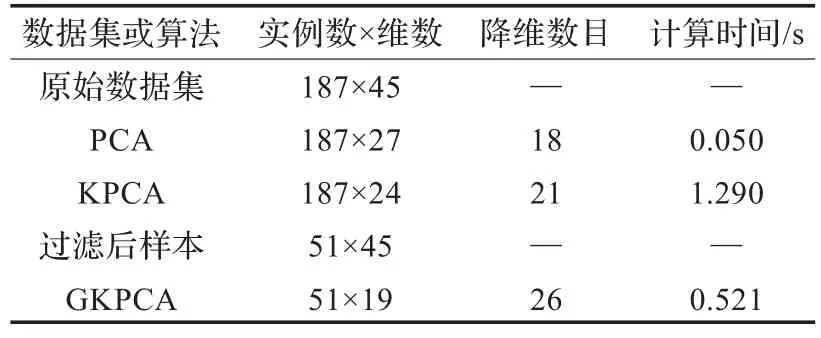
表1 数据集Spect降维结果

实验环境：本文在Matlab下对PCA、KPCA和GKPCA进行模拟仿真，配置环境为Pentium4，2.8 GHz CPU，内存1 GB，Windows XP操作系统，采用的数据流为“SPECTF心脏数据”（http：//archive.ics.uci.edu/ml/machine-learningdatabases/spect/），该数据集来源为美国俄亥俄州医学院，曾应用在“知识发现方法自动心脏显像诊断”（Artificial Intelligence in Medicine）。数据集描述心脏单个质子发射计算机断层显像（SPECT）影像诊断。每个病人分为两类：正常（1）和不正常（0）。测试数据集包含了187条实例，每条实例有45个属性，一组二进制数据和44组连续数据，连续数据取值为[0，100]。

测试结果：实验选取提取效率 p=0.95，过滤阈值ζ= 0.8，分组数为3，分析了PCA、KPCA和GKPCA算法的降维效果和计算时间，并进行了对比，图2～图5分别显示了原始数据集分布、PCA降维后数据分布、KPCA降维后数据分布和GKPCA降维后的数据分布。

通过降维结果分布图的对比与分析，可以看出，三种算法都有效地实现了数据降维，且相对于PCA和KPCA算法，GKPCA算法的降维效果更好。

表1对比了三种算法降维后的数据集维数和计算时间，从表1中可以看出，KPCA算法有效地实现了数据降维，但时间开销较大，GKPCA算法不仅实现了数据简约，而且缩短了计算时间。

以上测试是在小规模数据集上进行的，对于较大的数据集，采用了“阿拉伯口语数字数据集”（http：//archive.ics. uci.edu/ml/machine-learning-databases/00195/），该数据集显示了阿拉伯口语数字的梅尔频率倒普系数时间序列，数据来自阿拉伯本地的44位男性和44位女性。该数据集曾应用于语音识别等领域[15]。数据集包含两部分，一部分用于实验测试，共有87 063条实例，另一部分用于实验训练，共有269 856条实例，两个数据集中每行都含有13个梅尔频率属性。本实验截取测试数据集的部分数据，逐步增加测试用例，来检验PCA、KPCA与GKPCA的运行效率。

实验分别采取了189×n(1≤n≤7)个测试样例，选取提取效率 p=0.95，过滤阈值ζ=0.8，分组数为9，时间消耗如图6所示，降维效果如表2所示。

由图6可以看出，随着数据量的增大，PCA算法处理时间基本上没有发生变化，但KPCA的时间消耗呈指数级增长，在时间效率上，GKPCA对KPCA改进很大。由表2可以看出，PCA降维效果比较差，由原来的13维降为11或12维，KPCA比PCA降维效果好，但是时间消耗大，也不是理想的选择，GKPCA在保证时间消耗可以接受的范围内，有效地实现了数据流降维。

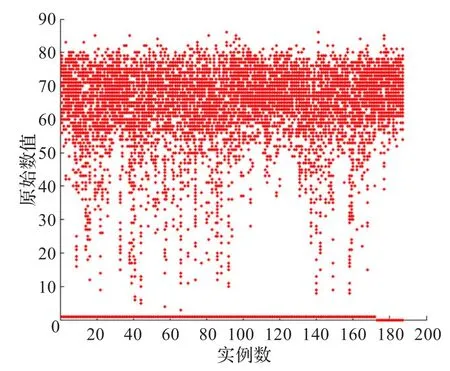
图2 原始数据分布图

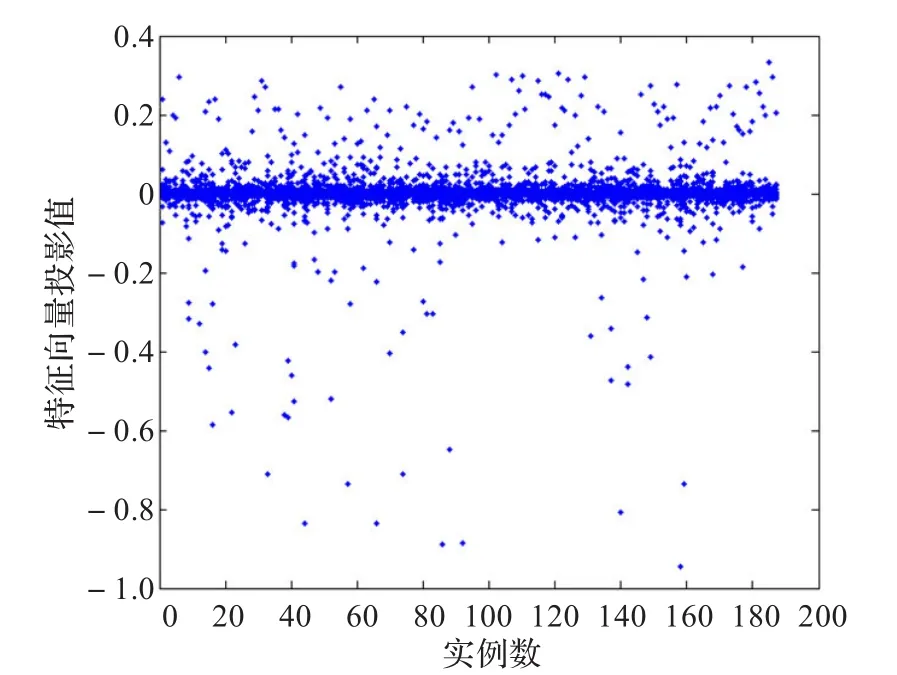
图4 经过KPCA降维后的数据分布

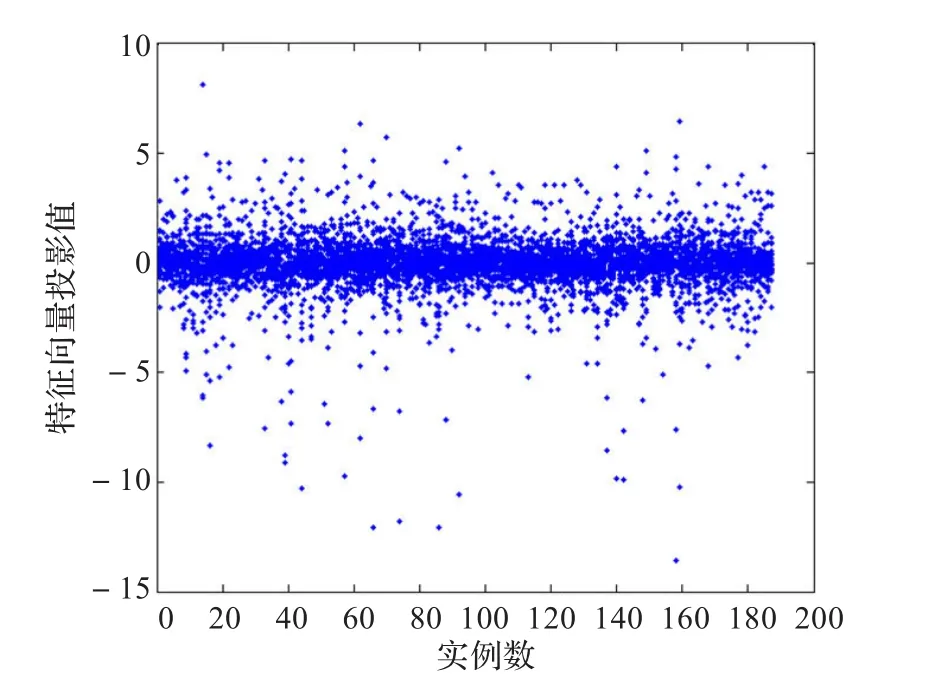
图3 经过PCA降维后的数据分布

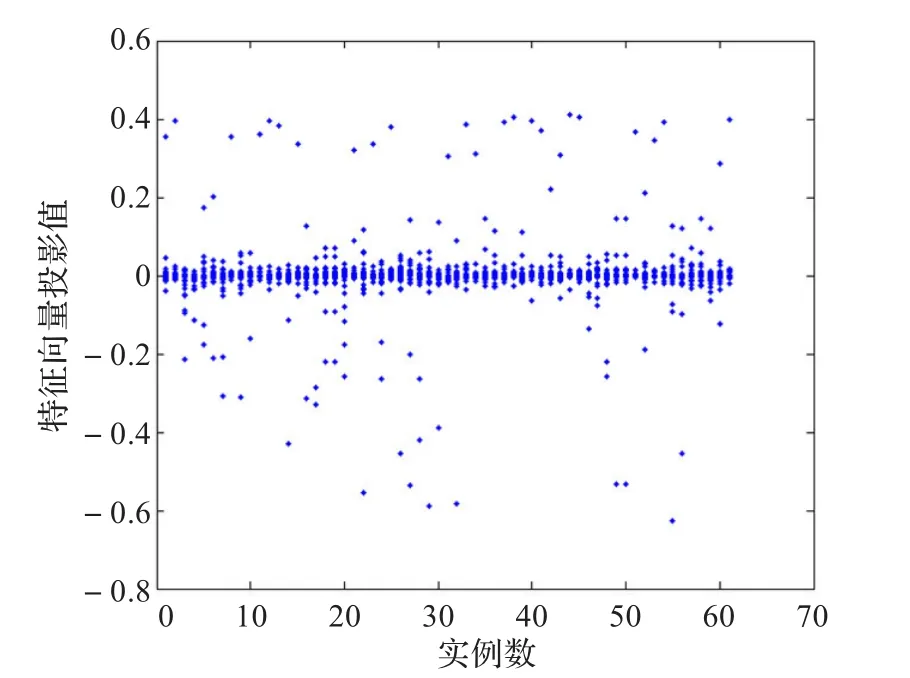
图5 经过GKPCA降维后的数据分布

表2 测试样例的降维结果

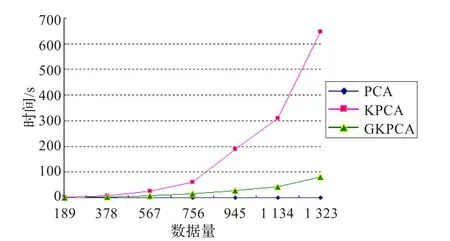
图6PCA、KPCA与GKPCA时间耗用图

4 结束语

KPCA其特点是特征提取速度快、特征信息保留充分，被广泛应用在信息处理中。实质上是在特征空间中进行PCA分析，在特征空间中，它有着和PCA相同的特性，既保留了PCA的优点，又有处理非线性问题的能力。KPCA又与PCA有着本质的区别：PCA是基于指标的，KPCA是基于样本的。KPCA不仅适合于解决非线性特征提取问题，而且还能获取比PCA更多的主分量。对于m条记录的n维样本，PCA能获取n个主分量，KPCA能获取m-1个主分量。

提出的GKPCA算法是KPCA算法的改进，主要在时间复杂度和空间复杂度上进行优化，提出样本分组和过滤策略，从而简化样本。实验表明，GKPCA算法在保证贡献率不降低的前提下，缩短了高维数据流降维时间，提高了降维效率。但核函数与样本参数都需要人为选择，这就容易对降维造成主观性误差，且随着数据量的增大，GKPCA仍然不会达到PCA的时间标准，KPCA算法仍有待改进。

[1]De Backer S，Naud A，Scheunders P.Non-linear dimensionality reduction techniques for unsupervised feature extraction[J]. Pattern Recognition Letters，1998，19：711-720.

[2]谭璐.高维数据的降维理论及应用[D].长沙：国防科技大学，2005：7-8.

[3]吴玲达，贺玲，蔡益朝.高维索引机制中的降维方法综述[J].计算机应用研究，2006，23（12）：4-7.

[4]Jolliffe I T.Principal component analysis[M].2nd ed.New York：Springer，2002.

[5]Saul L K，Roweis S T.An introduction to locally linear embedding[EB/OL].（2001-03-14）.http：//www.cs.nyu.edu/～roweis/lle/ publications.html.

[6]梁胜杰，张志华，崔立林.主成分分析法与核主成分分析法在机械噪声数据降维中的应用比较[J].中国机械工程，2011，22（1）：80-83.

[7]Tamilnadu S，Tamilnadu C.Enhancing face recognition using improved dimensionality reduction and feature extraction algorithms-an evaluation with orldatabase[J].International Journal of Engineering Science and Technology，2010，2（6）：2288-2295.

[8]Teixeira A R，Tomé A M，Stadlthanner K，et al.KPCA denoising and the pre-image problem revisited[J].DigitalSignal Processing，2008，18（4）：568-580.

[9]王瀛，郭雷，梁楠.基于优选样本的KPCA高光谱图像降维方法[J].光子学报，2011，40（6）：847-851.

[10]Burgers K，Fessehatsion Y，Rahmani S，et al.A comparative analysis of dimension reduction algorithms on hyperspectraldata[EB/OL].（2009-07-28）.http：//www.math.ucla.edu/～wittman.

[11]Rosipal R，Girolami M.An expectation-maximization approach to nonlinear componentanalysis[J].NeuralComputation，2001，13（1）：505-510.

[12]Baudat G，Anouar F.Generalized discriminant analysis using akernelfunction[J].NeuralComputing，2000，12（10）：2385-2404.

[13]王国胜.核函数的性质及其构造方法[J].计算机科学，2006：172-178.

[14]高绪伟.核PCA特征提取方法及其应用研究[D].南京：南京航空航天大学，2009：15-17.

[15]HammamiN，BeddaM.Improved tree model for arabic speechre cognition[C]//Proc IEEE ICCSIT10 Conference，2010.

基于核主成分分析的数据流降维研究

高宏宾，侯 杰，李瑞光

GAO Hongbin,HOU Jie,LI Ruiguang

School of Computer Science and Technology,Wuyi University,Jiangmen,Guangdong 529020,China

Theory and implementation of two data stream dimension reduction algorithms,PCA and KPCA,are analyzed.Due to linear PCA and KPCA can not effectively reduce data stream dimension when applied over large scale stream data,a new dimension reduction technique called GKPCA is proposed.With GKPCA,data sets are first partitioned into groups,and then KPCA is applied over each group.Data sets are filtered and regrouped into a new dataset.KPCA is again evaluated over the new data sets.This process is preceding recursively when some reduction threshold is reached which simplifies data stream sampling space and reduces time and space complexity of KPCA.Experimental analysis over different datasets illustrates that GKPCA can reduce data stream dimension excellently with less time consumption.

Kernel Principal Component Analysis（KPCA）;data stream;dimension reduction

分析了数据流降维算法PCA和KPCA的原理和实现方法。针对在大型数据集上PCA线性降维无法有效实现降维且KPCA的降维效率差，提出了一种新的降维策略GKPCA算法。该算法将数据集先分组，对每一组执行KPCA，然后过滤重新组合数据集，再次应用KPCA算法，达到简化样本空间，降低了时间复杂度和空间复杂度。实验分析表明，GKPCA算法不仅能取得良好的降维效果，而且时间消耗少。

核主成分分析；数据流；降维

A

TP39

10.3778/j.issn.1002-8331.1110-0295

GAO Hongbin,HOU Jie,LI Ruiguang.Research on dimension reduction of data stream based on kernel principal component analysis.Computer Engineering and Applications,2013,49（11）：105-109.

广东省自然科学基金（No.S2011010003681）。

高宏宾（1960—），男，在读博士，副教授，硕士生导师，主要研究领域为数据挖掘与分布式计算、算法设计与分析；侯杰（1986—），男，硕士研究生，CCF会员，研究方向为数据挖掘与分布式计算、算法设计与分析；李瑞光（1985—），男，硕士研究生，研究方向为数据挖掘与分布式计算、算法设计与分析。E-mail：tn10000@126.com

2011-10-17

2011-12-06

1002-8331（2013）11-0105-05

CNKI出版日期：2012-03-08 http://www.cnki.net/kcms/detail/11.2127.TP.20120308.1521.046.html