以互补条件熵为启发信息的正域属性约简

山西大学 计算机与信息技术学院 计算智能与中文信息处理教育部重点实验室，太原 030006

山西大学 计算机与信息技术学院 计算智能与中文信息处理教育部重点实验室，太原 030006

1 引言

粗糙集理论是一种处理不精确、不确定与不完全数据的数学工具[1-2]，其主要思想是：在保持信息系统分类能力不变的前提下，经过属性约简导出分类或决策规则。目前，粗糙集理论已经被广泛地应用于数据挖掘、机器学习、模式识别、故障诊断等领域[3-5]。

特征选择是指在不改变原始特征空间性质的前提下，从原始特征空间中选择一部分重要的特征，组成一个新的低维特征空间的过程。属性约简是在保持原始数据的属性区分能力不变的前提下，选择具有最小属性（特征）数量的属性子集的过程，是一种特定背景下的特征选择方法。属性约简是粗糙集理论中的核心内容之一。

目前，研究者已经提出了许多属性约简方法[6-8]。Skowron[6]提出了区分矩阵属性约简方法，该方法可以得到信息系统的所有约简，但是这种算法的复杂度过高（已经被证明为NP-Hard问题）。为了提高约简算法的效率，许多学者应用启发式的搜索策略求解属性约简，从而有效地降低约简算法的耗时。Hu和Cercone[7]将相对正域引入到属性约简中，提出了一种启发式属性约简算法。王国胤等[8-9]将Shannon信息熵用于属性子集评价，提出相应的启发式属性约简，该方法的停止条件也是利用Shannon条件熵。梁吉业等[10-14]将互补熵引入粗糙集理论用于度量信息系统的不确定性，并提出利用互补熵评价属性子集的属性约简算法。

上述启发式属性约简方法都是先根据前向贪婪搜索策略产生候选的属性子集，然后利用某种度量对候选属性子集进行评价，如果某个属性子集与原始属性集的区分能力相同（即满足停止条件），则得到属性约简，否则重复前面的过程直至满足停止条件（如图1所示）。这些算法都使用相同的度量作为属性子集的评价指标和算法的停止条件。评价指标决定着算法的收敛方向，而停止条件决定着算法得到的约简的性质，因此这两者并不必须使用相同的度量。

图1 属性约简过程示意图

根据上述分析，本文根据互补熵的随划分的变化规律，分四种情况分析了约简过程中当某个属性加入属性子集后，相对正域和互补条件熵的变化。并提出了一种以互补条件熵为启发信息、以相对正域为停止条件的属性约简方法，与传统的以相对正域为启发信息的正域约简算法相比，该算法可以得到属性数量更少的约简，同时计算约简的时间消耗也更少。

2 基本概念

设S=(U，A，V，f)为一个信息系统，其中U为非空有限对象集合，称为论域；A为非空有限属性集合；对任意a∈A有 a:U→Va，其中Va称为属性 a 的值域，V=∪a∈AVa，f:U×A=V是一个函数，对于任意的a∈A有 f(x，a)∈Va。

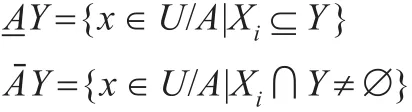
称集合 BNR(Y)=-为Y的 R边界域；POSR(Y)=为Y的 R正域；NEGR(Y)=U-RY为Y的 R负域。

若信息系统中的属性集 A=C∪D，C表示条件属性集，D表示决策属性集，C∩D≠，则该信息系统称为一个决策表，记为DT=(U，C∪D，V，f)。如果其中条件属性集C对论域U的划分为={X1，X2，…，Xm}，决策属性集D对论域U的划分为={Y1，Y2，…，Yn}，则 D 关于C的相对正域记为POSC。若某个决策表的决策属性集关于条件属性集的相对正域为整个论域，则称其为协调的决策表，否则称其为不协调的决策表。

基于互补条件熵可以给出属性a关于属性集C重要度 SGF(a，C，D)的定义：

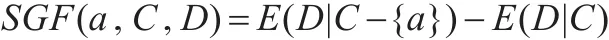
3 以互补熵为启发信息的属性约简

为了给出新的属性约简算法，首先引入下面的定理。

定理1[15]给定决策表 DT=(U，C∪D，V，f)，C 是条件属性集，D是决策属性集。若U/B≻U/C，则

定理1表明随着论域划分的变细，决策表的互补条件熵将变小。

定理2[16]给定决策表 DT=(U，C∪D，V，f)，C 是条件属性集，B⊆C，D是决策属性集，则

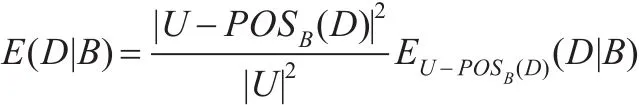
定理2表明互补条件熵不仅与其正域部分的大小有关，还与其非正域部分的互补条件熵的大小有关。进一步结合定理1的结论可以得出非正域部分的条件熵的大小与其划分的粗细程度有关。因此，利用互补条件熵作为启发式信息，则不但可以反映正域部分大小，也可以反映非正域部分的分布情况（划分的粗细程度）。

在属性约简的过程中，决策属性关于当前属性集的非正域部分中对象将会成为下一次迭代时相对正域中的对象，如图2所示，图中决策属性关于属性集B的非正域中的一些对象（阴影部分）在条件属性集为B∪{ai}时进入了相对正域。因此，决策属性集关于某一条件属性集的非正域中的对象的分布情况也会对约简过程中属性的选择产生重要的影响，进而影响约简算法收敛的方向和速度。

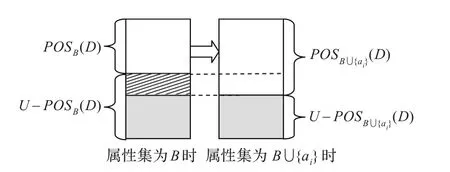
图2 约简过程中相对正域和非正域的变化

为了更好地说明约简过程中以互补条件熵为启发信息和以正域为启发信息的区别，下面分四种情况来分析。

不失一般性，不妨设当前属性子集为B，可选择加入的属性有ai和aj。

为了说明该情况时在论域U下互补条件熵的变化情况，给出下面的定理3。

定理3 给定决策表 DT=(U，C∪D，V，f)，C 是条件属性集，D是决策属性集，B⊆C。若对于任意的属性ai和aj，POSB∪{ai}(D)=POSB∪{aj}(D)， 且 U-POSB∪{ai}(D)/(B ∪{ai})≻U-POSB∪{aj}(D)/(B∪{aj})，则

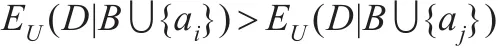
证明根据已知条件(U-POSB∪{ai}(D))/(B∪{ai})≻(UPOSB∪{aj}(D))/(B∪{aj})和定理 1，可以得到(D|B ∪{ai})＞(D|B∪{aj})。

证毕。

根据定理3可以得出，在约简过程中当两个属性ai和aj分别加入的候选属性子集B时，如果决策属性集D关于B∪{ai}的相对正域与关于B∪{aj}的相对正域大小相等，且属性B∪{ai}对非正域部分的划分比B∪{aj}对非正域部分的划分细，则在论域U下，D关于B∪{ai}的互补条件熵较小。

因此，在约简过程中，出现情况1时，若选择正域作为启发式信息，则属性ai和aj的重要程度相同，只能任意选择一个。而选择互补条件熵为启发信息则可以选择到对非正域部分划分更细的属性，为约简过程的下一次迭代奠定更好基础。

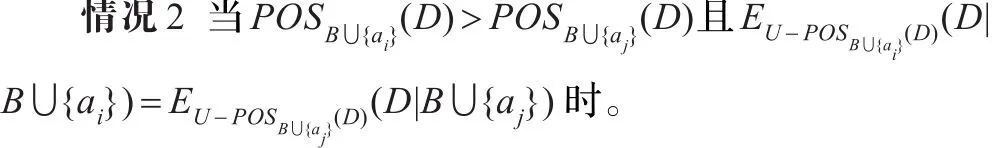
为了说明该情况时在论域U下互补条件熵的变化情况，给出下面的定理4。

定理4 给定决策表 DT=(U，C∪D，V，f)，C 是条件属性集，D是决策属性集，B⊆C。若对于任意的属性ai和aj，POSB∪{ai}(D)＞ POSB∪{aj}(D) 且(D|B ∪{ai})=(D|B ∪{aj})，则

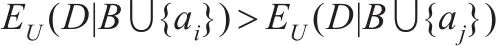
类似于定理3，容易证明定理4。

定理4表明在约简过程中当两个属性ai和aj分别加入候选属性子集B时，如果在决策表的非正域部分B∪{ai}关于决策属性的互补条件熵与B∪{aj}关于决策属性的互补条件熵相等，且在论域U上D关于B∪{ai}相对正域比D关于B∪{aj}相对正域大，则在论域U上D关于B∪{ai}关的互补条件熵较小。

因此，在约简过程中，出现情况2时利用正域和互补条件熵作为启发信息，都会选择并入属性子集B后使得相对正域更大的属性ai。

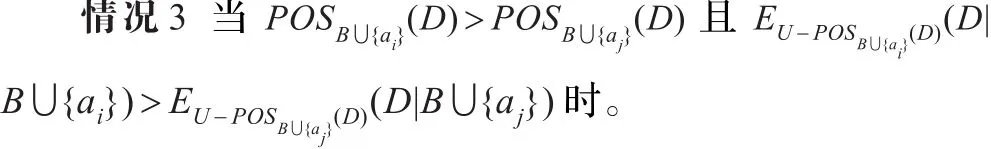
为了说明该情况时在论域U下互补条件熵的变化情况，给出下面的定理5。

定理5 给定决策表 DT=(U，C∪D，V，f)，C 是条件属性集，D是决策属性集，B⊆C。若对于任意的属性ai和aj，(D)＞POSB∪{aj}(D)且 (U-(D))/(B∪{ai})≺(U-(D))/(B∪{aj})，则

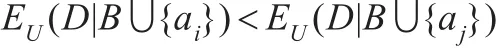
类似于定理3，容易证明定理5。

根据定理5可以得出，在约简过程中当两个属性ai和aj分别加入到候选属性子集B中，如果决策属性集D关于B∪{ai}的相对正域比关于 B∪{aj}的相对正域大，且B∪{ai}对非正域部分的划分比B∪{aj}非正域部分的划分更细，则在论域U下D关于B∪{ai}的互补条件熵较小。

因此，在约简过程中，出现情况3时利用正域和互补条件熵作为启发信息，都会选择并入属性子集B使得相对正域更大的属性ai。

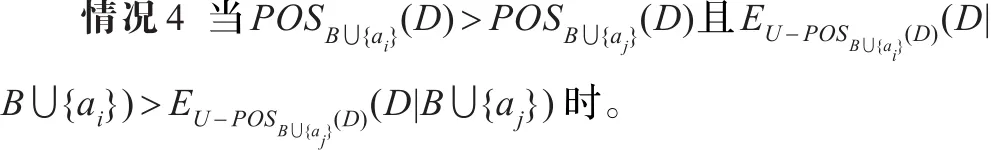
在约简过程中，当两个属性ai和aj分别加入的候选属性子集B中，如果决策属性集D关于B∪{ai}的相对正域比关于B∪{aj}产生的相对正域大，且B∪{ai}对非正域部分的划分比B∪{aj}对非正域部分的划分粗糙，则在论域U下属性子集B∪{ai}的互补条件熵与属性子集B∪{ai}关于决策表的互补条件熵大小关系无法确定。

因此，当约简过程中出现情况4时，若利用正域和互补条件熵作为启发信息，则选择产生相对正域较大的属性ai并入属性子集B；若利用互补条件熵作为启发信息，则能够综合考虑属性加入后新的属性子集产生相对正域的大小和对于非正域部分划分的粗细程度选择属性。这样更有利于为约简过程的下一次迭代提供好的属性。

根据上述分析，本文设计了以互补条件熵为启发信息的正域约简算法，该算法的具体描述如下：

算法1以互补条件熵为启发信息的正域约简算法（CE-PRAR）

表2 算法CE-PRAR和PR-PRAR运行结果和运行时间对比

输入一个决策表T=(U，C∪D，V，f)

输出决策表的相对约简red

步骤1 red←;//red用来存放候选属性子集。

步骤2如果(D)-POSC(D)＜0，则将ai放入red//计算核属性。

步骤3当 POSred(D)≠POSC(D)时，//停止条件执行{red←red∪{a0}，其中Sig(a0，red，D)={Sig(ak，red，D)}}。

步骤4返回red，结束。

下面分析该算法的时间复杂性。设DT=(U，C∪D，V，f)，其中C∪D=ϕ，C是条件属性集合，D是决策属性集合。若|C|=m，|U|=n，则算法的时间复杂度为O(mn2)+O(n3)。

4 实验及分析

为验证本文提出的CE-PRAR算法的性能，本文选取了UCI数据库中的6组数据集进行测试，分别比较了以互补条件熵为启发信息的正域约简算法（CE-PRAR）和以正域为启发信息正域约简（PR-PRAR）的约简结果和时间消耗。实验中使用的数据集的详细信息见表1。

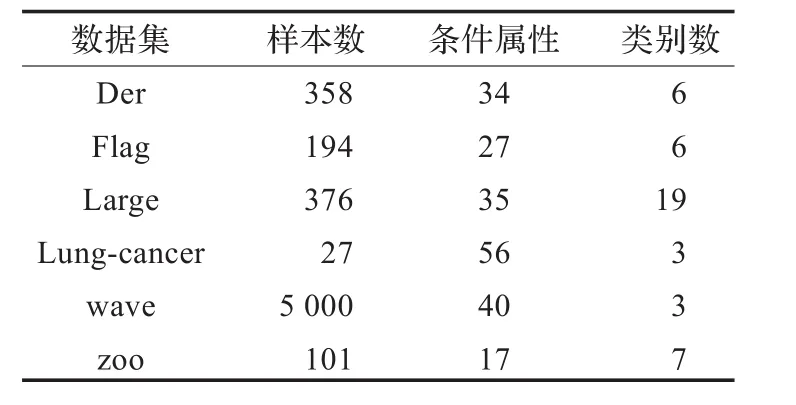
表1 实验用UCI数据集

实验在硬件配置为CPU Pentium 3.40 GHz、内存2 GB的计算机上，用C#语言编程实现算法，开发和测试平台为Microsoft Visual Studio 2005。

表2给出了利用算法CE-PRAR和PR-PRAR在表1中的6个UCI数据集上的约简结果和时间消耗。从表2中可以看出对于大多数数据集由算法CE-PRAR获得的约简的属性数量比利用算法PR-PRAR获得的约简的属性数量少，并且计算耗时也明显变少。在Der、Flag、large、Waveform和Zoo数据集利用算法CE-PRAR得到的约简均比利用算法PR-PRAR得到的约简少1个属性，而且算法CE-PRAR的时间消耗比算法PR-PRAR也要小。特别是在数据集Lung-cancer上效果更为明显，算法CE-PRAR得到的约简属性的数量比算法PR-PRAR得到的约简的属性数量少两个，而且与算法CE-PRAR相比时间消耗明显较小。

为了说明算法CE-PRAR的有效性，利用文献[17]中提出的决策表决策性能评价指标（确定度α、协调度 β和支持度γ）对利用算法CE-PRAR和算法PR-PRAR约简后决策表的决策性能进行了对比分析（如表3所示）。从实验结果中可以看出对于所有的实验数据集，经算法CE-PRAR约简后的决策表的决策性能与经算法PR-PRAR约简后决策表的确定度α、协调度 β和支持度γ的值均相同或相差很小，这说明利用算法CE-PRAR和算法PR-PRAR得到的约简决策表的决策性能非常接近。

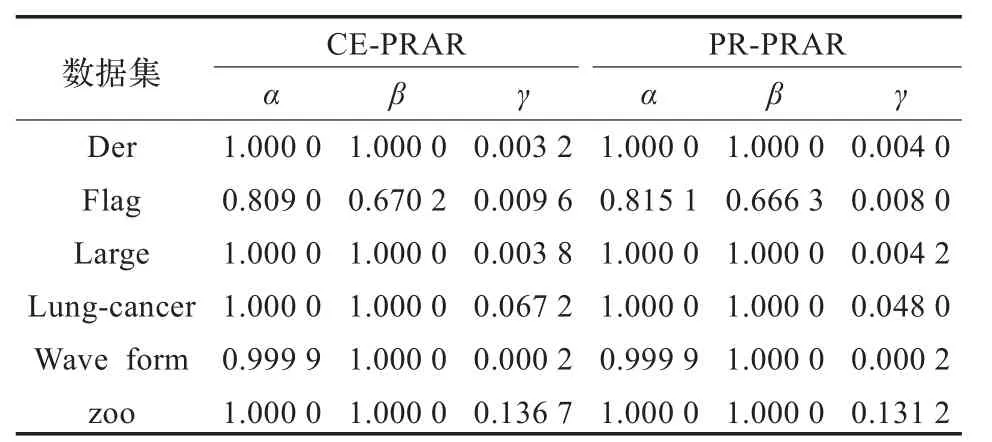
表3 经算法CE-PRAR和PR-PRAR约简后决策表的决策性能对比

5 结论

本文对常见的属性约简方法进行了深入分析，发现在其约简过程中，候选属性子集的评价指标和算法的停止条件都是使用相同的度量，而在正域约简中使用相对正域作为这两个指标。进一步，根据互补熵的随划分的变化规律，分四种情况分析了约简过程中某个属性加入候选属性子集后，相对正域和互补条件熵的变化，发现以互补条件熵作为启发信息不但可以反映约简过程中相对正域大小的变化，还能够反映非正域部分的分布变化。最后，提出了一种以互补熵为启发信息的正域属性约简算法。实验结果表明，提出的新算法与以相对正域为启发信息的正域约简算法相比，可获得一个包含更少属性且决策性能非常接近的约简，而且新算法的时间消耗也明显减少。

[1]张文修，吴伟志，梁吉业，等.粗糙集理论与方法[M].北京：科学出版社，2001.

[2]Pawlak Z.Rough sets theoretical aspects of reasoning about data[M].[S.l.]：Kluwer Academic Publishers，1991.

[3]张文修，梁怡，吴伟志.信息系统与知识发现[M].北京：科学出版社，2003：7-12.

[4]Pedrycz W，Vukovich G.Feature analysis through information granulation and fuzzy sets[J].Pattern Recognition，2002，35：825-834.

[5]Greco S，Pawlak Z，Slowinski R.Can Bayesian confirmation measures be useful for rough set decision rules[J].Engineering Applications of Artificial Intelligence，2004，17：345-361.

[6]Skowron A，Rauszer C.The discernibility matrices and functions in information tables[M]//Intelligent decision support：handbook of applications and advances of rough set theory. Dordrecht：Kluwer Academic Publishers，1992：331-362.

[7]Hu X H，Cercone N.Learning in relationaldatabases：a rough set approach[J].International Journal of Computational Intelligence，1995，11（2）：323-338.

[8]王国胤.决策表核属性的计算方法[J].计算机学报，2003，26（5）：611-615.

[9]王国胤，于洪，杨大春.基于条件信息熵的决策表约简[J].计算机学报，2002，25（7）：759-766.

[10]Liang J Y，Chin K S，Dang C Y，et al.A new method for measuring uncertainty and fuzziness in rough set theory[J]. InternationalJournalofGeneralSystems，2002，31（4）：331-342.

[11]Wei W，Liang J Y，Qian Y H，et al.An attribute reduction approach and its accelerated version for hybrid data[C]// The 8th IEEE International Conference on Cognitive Informatics，2009：167-173.

[12]Wei W，Liang J Y，Qian Y H，et al.Comparative study of decision performance of decision tables induced by attribute reductions[J].International Journal of General Systems，2010，39（8）：813-838.

[13]Wei W，Liang J Y，Qian Y H.A comparative study of rough sets for hybrid data[J].Information Sciences，2012，190（1）：1-16.

[14]梁吉业，魏巍，钱宇华.一种基于条件熵的增量核求解方法[J].系统工程理论与实践，2008，28（4）：81-89.

[15]梁吉业，李德玉.信息系统中的不确定性与知识获取[M].北京：科学出版社，2005：37-46.

[16]Qian Y H，Liang J Y，Pedrycz W，et al.Positive approximation：an accelerator for attribute reduction in rough set theory[J].Artificial Intelligences，2010，174（9/10）：597-618.

[17]Qian Y H，Liang J Y，Li D Y，et al.Measures for evaluating the decision performance of a decision table in rough set theory[J].Information Sciences，2008，178（1）：181-202.

以互补条件熵为启发信息的正域属性约简

魏 巍，陈红星，王 锋

WEI Wei,CHEN Hongxing,WANG Feng

Key Lab of MoE for Computation Intelligence&Chinese Information Processing,School of Computer&Information Technology, Shanxi University,Taiyuan 030006,China

Attribute reduction,as a special approach for feature selection,is a key concept in rough set theory.The positive-region reduction approach is a kind of common reduction approach,which is of greedy and forward search type.These approaches keep adding one attribute with high significance into a pool during each iteration until positive-region no longer changes.In this paper, by analyzing changes of complementary conditional entropy varying with partition,four situations about changes of positive-region and entropy induced by adding a new attribute to the candidate attribute set are introduced.Then,a positive-region reduction algorithm based on complementary entropy is developed.Experimental results show that compared with the traditional positiveregion reduction algorithm,the proposed algorithm can find a reduction including fewer attributes and possessing almost same decision performance in a significantly shorter time.

rough set;attribute reduction;complement entropy;positive region

属性约简是一种特殊的特征选择方法，是粗糙集理论中的核心内容之一。正域约简是一类常见的启发式的约简方法，它通常采用前向贪婪搜索策略产生候选的属性子集，以相对正域作为启发信息和停止条件。根据互补条件熵的随划分的变化规律，分四种情况分析了约简过程中某个属性加入属性子集后，相对正域和互补条件熵的变化，并在此基础上提出了一种以互补熵为启发信息的正域属性约简方法。实验分析表明，新方法与传统的正域约简算法相比，可以得到属性数量更少且决策性能非常接近的约简，同时可以有效地提高约简计算效率。

粗糙集；属性约简；互补熵；正域

A

TP393

10.3778/j.issn.1002-8331.1212-0094

WEI Wei,CHEN Hongxing,WANG Feng.Positive region attribute reduction utilizing complement condition entropy as heuristic information.Computer Engineering and Applications,2013,49（11）：96-100.

国家自然科学基金（No.71031006，No.61202018，No.60970014）；山西省自然科学基金（No.2010021017-3）。

魏巍（1980—），男，博士，讲师，主要研究方向为数据挖掘、粒度计算；陈红星（1963—），男，工程师，主要研究方向为概念格、数据挖掘；王锋（1984—），女，博士研究究生，主要研究方向为粒度计算、模式识别。E-mail：weiwei@sxu.edu.cn

2012-12-10

2013-02-18

1002-8331（2013）11-0096-05