无限大功能梯度材料反平面裂纹应力场
2013-08-01胡志新张雪霞
胡志新,张雪霞,李 婵
(太原科技大学应用科学学院,太原030024)
近几年,为满足一些新技术尤其微电子、航空航天和高温应用等对材料的苛刻要求,一种新型材料(功能梯度材料)的概念被引入到了工程结构中。从应用力学方面来看,功能梯度材料具有的优越性能主要是不均匀性,不仅使其具有较好的热机性能而且更具有良好的屈服应力、断裂韧性、疲劳和蠕变等基本力学行为。目前,已经有许多关于材料非均匀性的研究[1-5]。与功能梯度材料相关的大多数的研究都集中在各向同性体。但事实上,各向同性功能梯度材料[6]不多见。
近几年有相当多学者采用不同的材料模型,对功能梯度正交各向异性材料的反平面问题进行了研究。文献[1]采用模型 μ(z)=μ0|z|m(m>0),μ(z)=μ0(c+|z|)m,文献[7-8]中采用μ(z)=μ0(1+α|z|)2模型。
上述文献中材料物性参数采用的是都是单参数模型,而本文中的材料物性参数采用了双参数三次幂函数模型。采用了积分变换-对偶积分方程的方法,研究含有限尺寸裂纹的无限大功能梯度材料的静态应力强度因子,并考察无量纲应力强度因子ψ(1)随着不均匀系数r以及裂纹长度a的变化情况。研究结果表明:应力强度因子ψ(1)随着r的增加而增加,随着a的增加而增加,这一结果为功能梯度的断裂研究提供了重要的理论意义。
1 材料物性参数的幂函数模型
设无限大功能梯度正交各向异性材料,如图1所示,x轴和y轴是正交主轴,剪切模量μx,μy是y的函数,并且μx,μy是按下列梯度变化的。即:
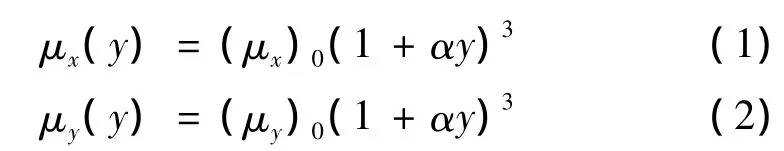
其中不均匀性参数α>0,(μx)0和(μy)0是y=0的剪切模量。
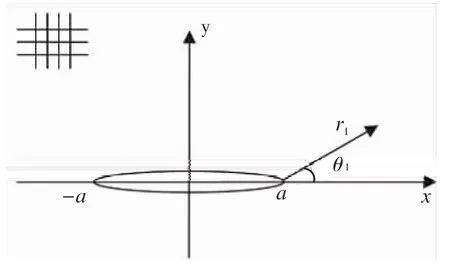
图1 含有限裂纹的功能梯度材料Fig.1 Functionally-graded material with finite length crack
2 偏微分方程和边界条件的建立
假设y=0平面有一条长是2a的裂纹,裂纹面受到了反平面剪切载荷下的作用,x,y和z方向的位移分量分别为ux,uy和uz.ux,uy处处为 0,uz=ω(x,y),非零应力分量 τxz和 τyz如下:

已知其应力平衡方程是:

将式(3)代入式(4)中,可以得到控制方程:
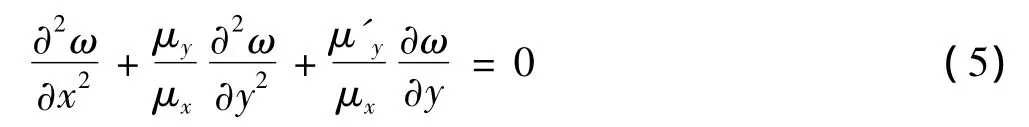
无限大功能梯度正交各向异性材料反平面裂纹问题的边界条件是:
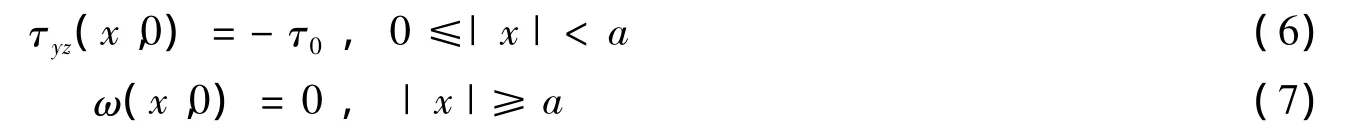
因此,功能梯度材料反平面裂纹的问题就被转化成了求解偏微分方程的边值问题。
3 导出对偶积分方程
由于裂纹的对称性,只需要考虑x>0,y>0的平面。引入以下关于x的Fourier余弦变换:
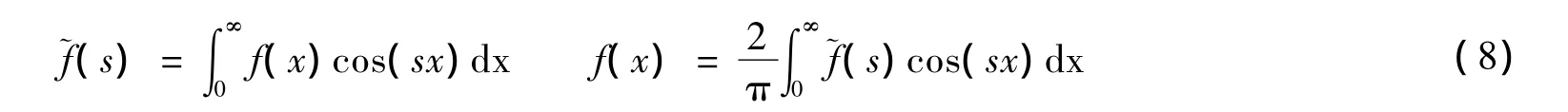
即令
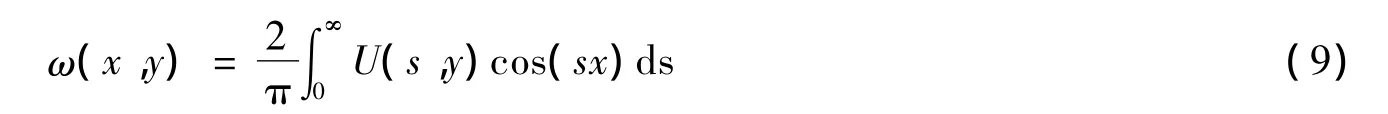
将式(9)代入式(5)可得方程如下:
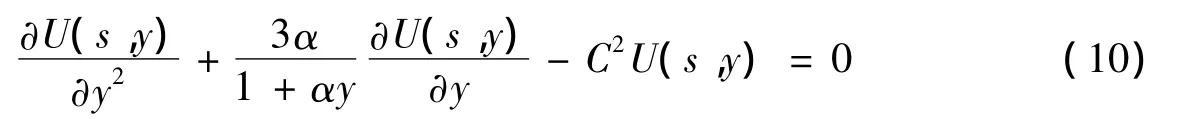
其中
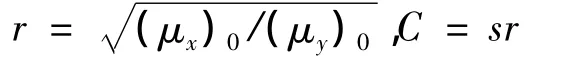
得到修正贝塞尔方程:

其中A1、B1是解的系数,I1()、K1()分别是第一类和第二类Bessel函数。
考虑y→∞ 处的正则条件,方程式(11)的解可表示为:
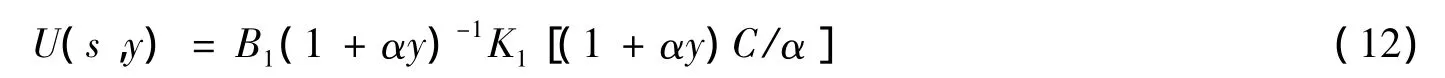
将式(12)代入式(9)得
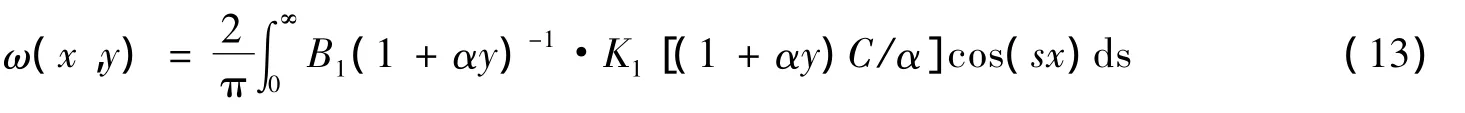
将式(13)代入式(3)得到剪切应力τxz和τyz的积分表达式:
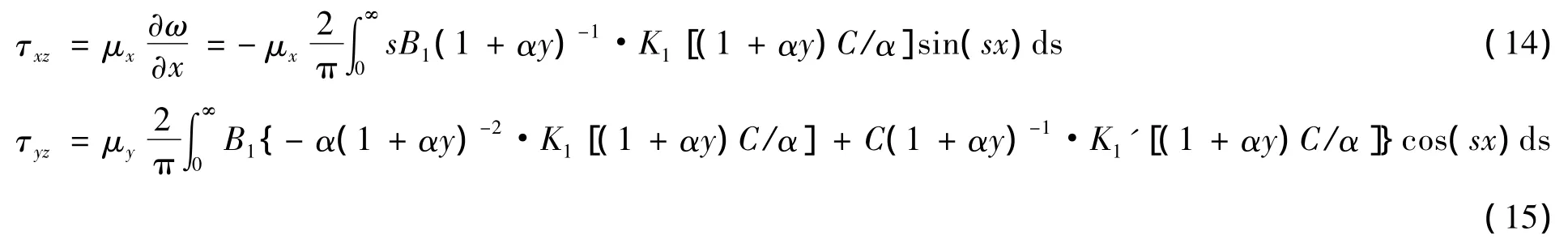
由式(13)、式(15)及边界条件式(6)、式(7)得到对偶积分方程:
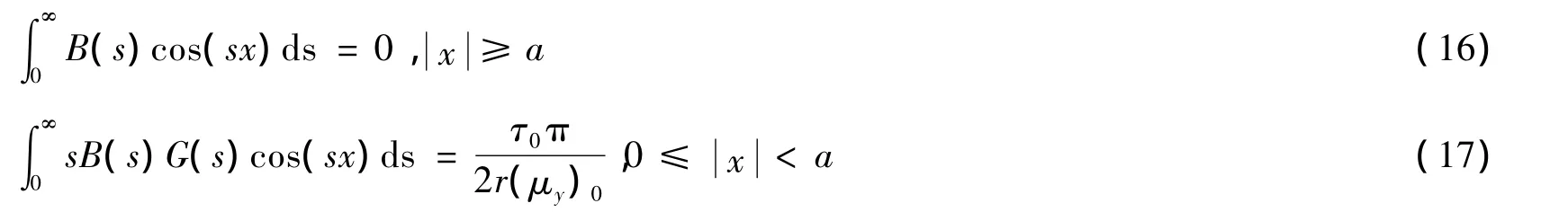
采用Copson方法[9],求解对偶积分方程,得到对偶积分方程的解为:
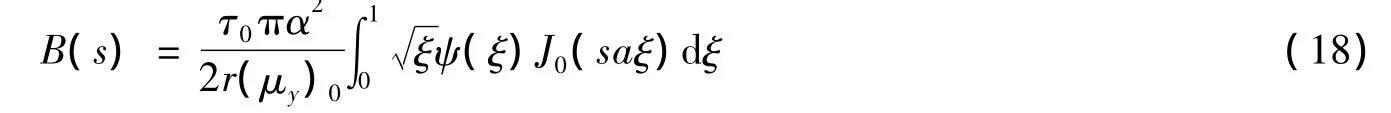
其中J0()是零阶第一类Bessel函数,函数ψ(ξ)由以下第二类Fredholm积分方程控制:
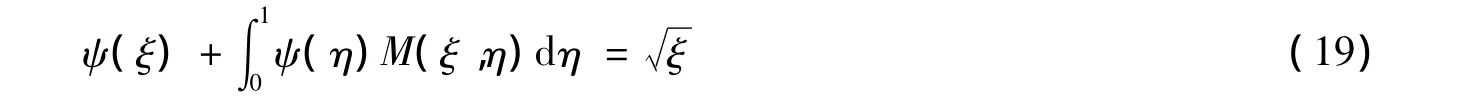
核:
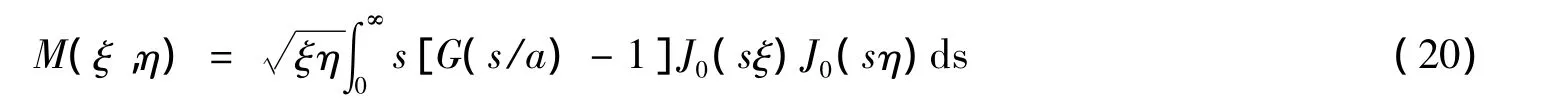
通过数值求解式(19)、式(20)可以得到ψ(1).
4 裂纹尖端应力场及应力强度因子
为了对式(18)进行分部积分,引入Bessel函数的求导公式:
这里v是Bessel函数的阶,z是Bessel函数的变量。
下面对式(18)进行分部积分:
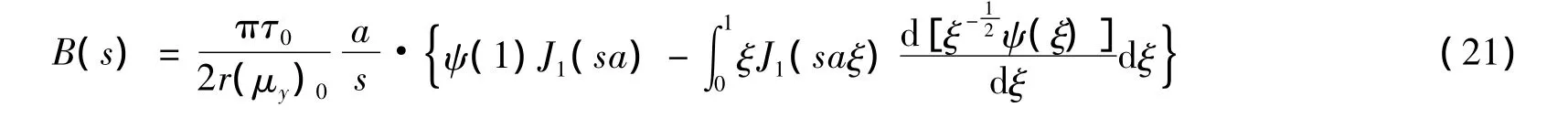
将式(21)代入式(14)、式(15),并且利用B(s)=B1K1(C/α)得:
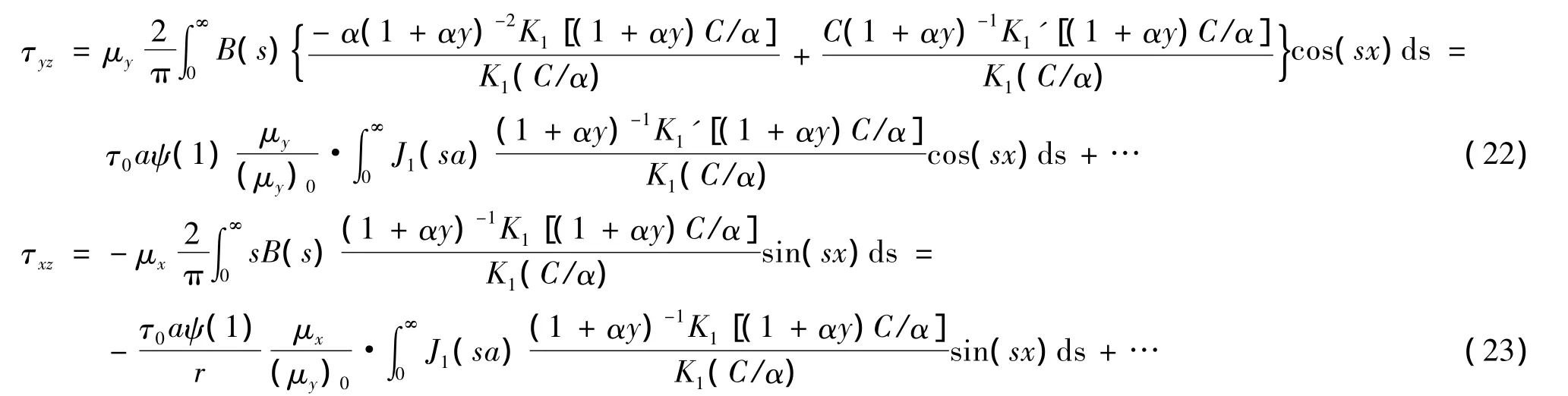
考虑式(22)、式(23)在s→∞ 处的积分发散性以及x→∞ 时Kβ(x)和Kβ'(x)的一些渐进特性[10]:
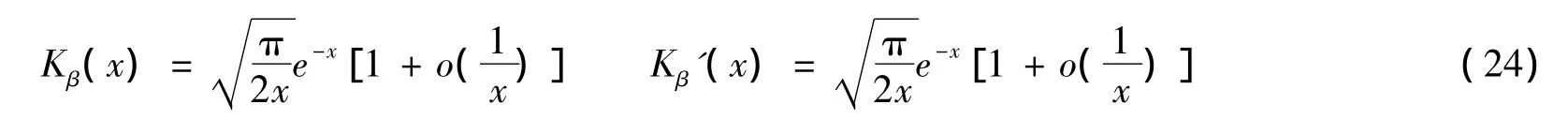
定义复变量z0=x+iry,则有:
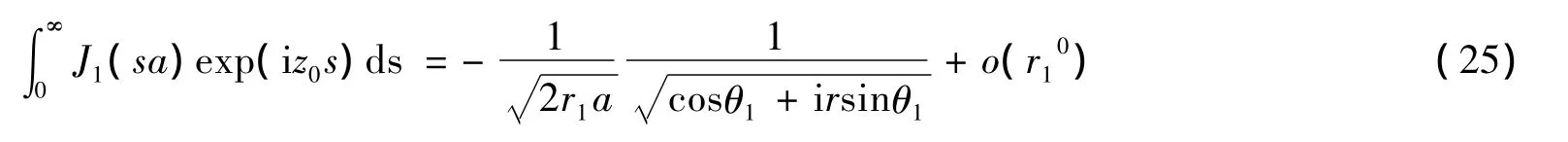
这里r1和θ1在图1中有定义。
第一类一阶Bessel函数满足如下条件:
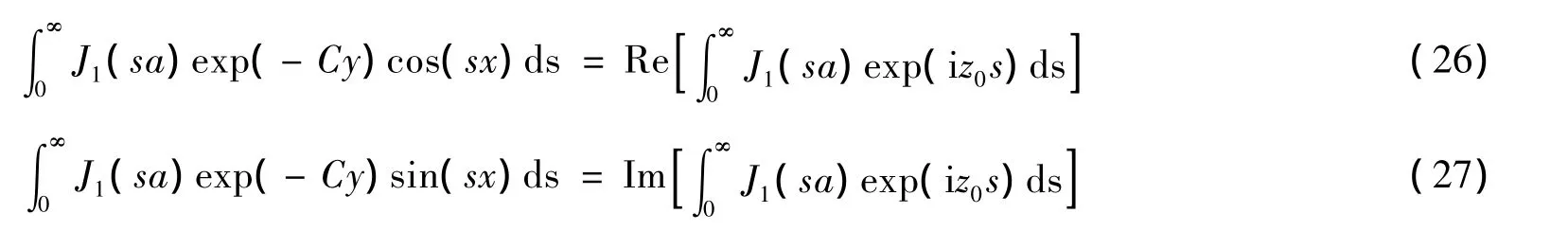
由式(22)-式(27)得到:
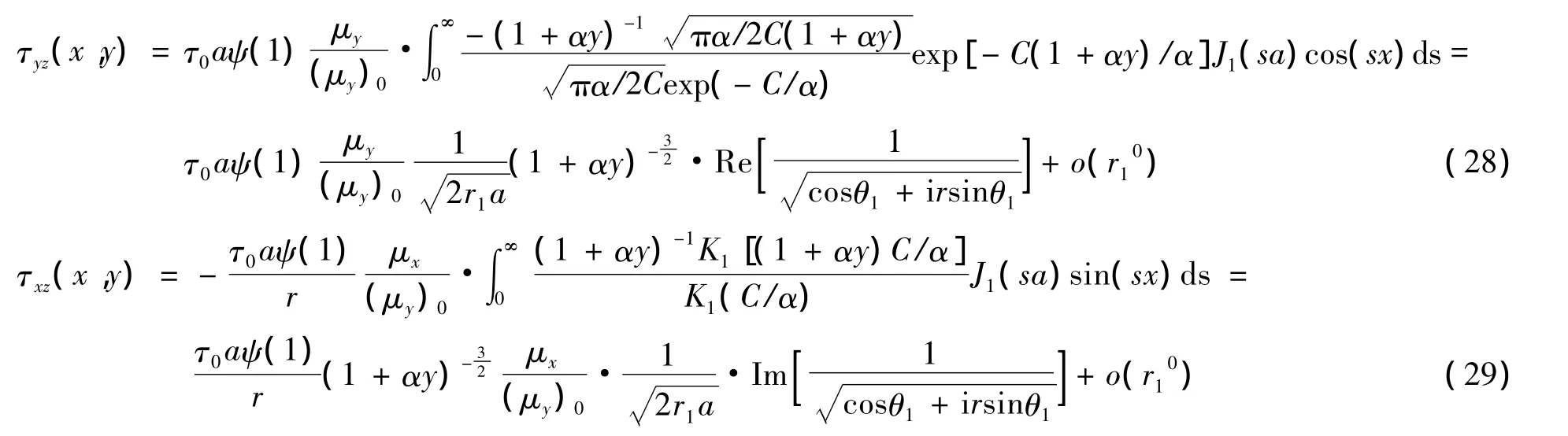
根据图1所示,由直角坐标到极坐标的转换式如下:
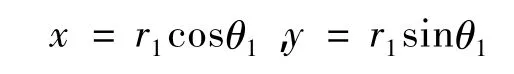
考虑到式(28)、式(29)在r1→0处的变化情况,整理可得:
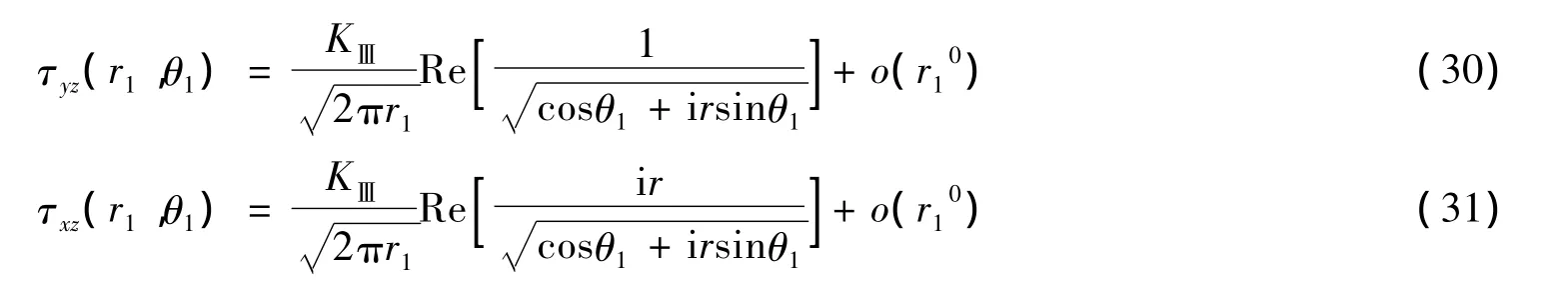
由式(30)、式(31)得到应力强度因子的表达式:

式(32)可变形为:

这里ψ(1)称为无量纲应力强度因子。
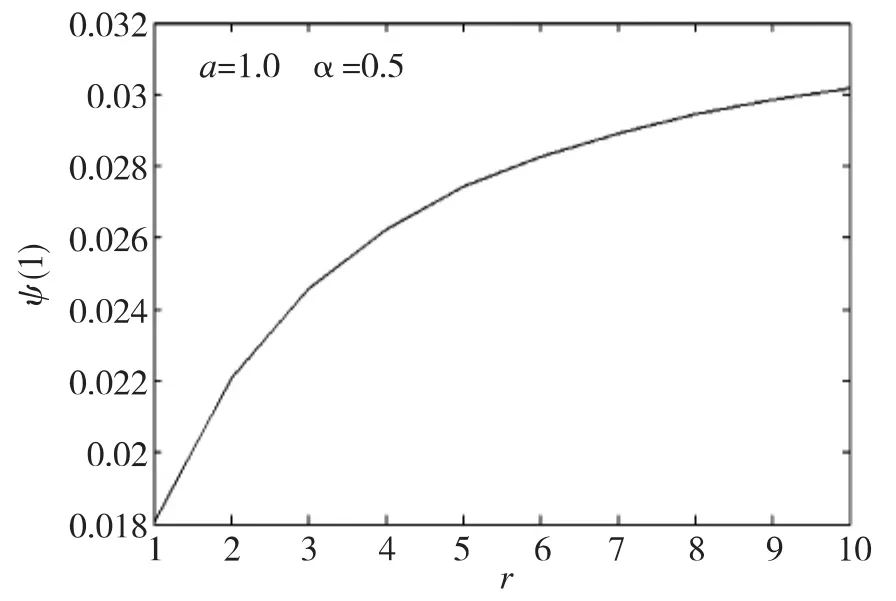
图2 无量纲应力强度因子ψ(1)随着不均匀系数r的变化曲线Fig.2 The variation curves of the dimensionless stress intensity factor ψ(1)with the nonhomogeneous coefficient r
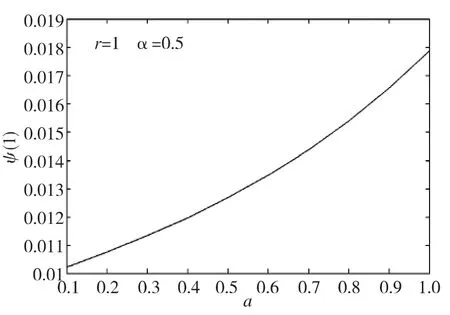
图3 无量纲应力强度因子ψ(1)随着裂纹长度a的变化曲线Fig.3 The variation curves of the dimensionless stress intensity factor ψ(1)with the crack length a
如图2和图3所示:利用数学软件Matlab分析了无量纲应力强度因子ψ(1)随着不均匀系数r和裂纹长度a的变化曲线。
5 结论
(1)从式(27)、式(28)中可以得到,功能梯度正交各向异性材料的裂纹尖端场具有的奇异性,并且极角θ1的角分布函数与正交各向异性均匀材料的情况是相同的,这一结论与功能梯度各向同性材料反平面问题的结论是一致的。
(2)如图2与图3所示,借助matlab软件数值分析了无量纲应力强度因子ψ(1)与不均匀系数r和裂纹长度a的变化关系。图2中显示了ψ(1)随着r增加而增加的变化曲线,也就是说,通过增大垂直于裂纹面的剪切模量可以抑制裂纹的扩展驱动力,这与文献[10]中的结论一致。图3中显示了ψ(1)随着a增加而增加的变化曲线,这一结论让我们知道了应力强度因子与裂纹的尺寸大小有密切的关系,而且裂纹尺寸大小对应力强度因子的影响很大,这是对前人工作的改进与创新。
[1]ERDOGAN F.The crack problem for bonded nonhomogeneous materials underantiplane shear loading[J].ASME Journal of Applied Mechanics,1985,52(4):823-828.
[2]KONDA N,ERDOGAN F.The mixed mode crack problem in a nonhomogeneous Elastic medium[J].Engineering Fracture Mechanics,1994,47(4):533-545.
[3]ERDOGAN F.Fracture mechanics of functionally graded material[J].Composities Engineering,1995,5(7):753-770.
[4]隋中和,李俊林.正交各向异性功能梯度材料反平面断裂力学分析[J].太原科技大学学报,2007,28(4)321-323.
[5]高廷凯,杨维阳.功能梯度材料平面断裂中的一系列偏微分方程边值问题[J].太原科技大学学报,2006,27(1)33-38.
[6]MAHAJIAN R,ERDOGAN F.Cracking of an orthotropic substrate reinforced by an orthotropic plate[J].International Journal of Solids and Structures,2003,23(40):6389-6415.
[7]LI C Y,ZOU Z Z,DUAN Z P.Dynamic stress field around the mode Crack tip in an orthotropic functionally graded material[J].Appl Math Mach,2000,21:651-658.
[8]OZTURK M,ERDOGAN F.Mode crack problem in an inhomogeneous orthotropic medium[J].Int J Engng Sci,1997,35(9):869-883.
[9]COPSON E T.On certain dual integral equations[J].Proceedings Glasgow Mathematical Association,1961(5):19-24.
[10]李春雨.功能梯度材料静动态断裂力学研究[D].哈尔滨:哈尔滨工业大学,1999.
