面向机械设计的一种改进的遗传算法
2013-08-01洪朝飞陶元芳
洪朝飞,陶元芳,潘 鲜
(1.太原科技大学机械工程学院,太原030024;2.江苏省特种设备安全监督研究院无锡分院,江苏无锡214174)
近年来,中国的机械制造业发展迅速,然而中国机械工业在技术创新、新产品开发、产品档次等方面与国际领先水平还有很大差距。增加产业利润、提升产业竞争力除需加大理论研究与技术创新之外,新的设计方法的应用也是重要的一个途径[1]。
遗传算法(Genetic Algorithm)是一种广泛用于NP难问题的群智能优化算法,将生物的遗传与进化的一些基本概念和机理引申到解决工程问题之中[2]。至今,遗传算法已被成功地应用于工业管理、交通运输、工业设计等机械工程领域[3]。但由于机械产品设计问题一般为组合优化与非线性规划相结合的问题,同时约束非常复杂,数学模型往往为多极值、可行域稀疏,目标函数和约束为大规模非线性或没有解析表达式的形式。本文提出一种改进的小生境变种群规模遗传算法,针对机械设计模型的特点,提升遗传算法在解决机械设计问题中的性能。
1 遗传算法在机械设计中的应用
现今机械制造日益向系列化、小批量化、专业化方向发展。要求企业缩短设计周期并且在满足产品品质的基础上尽量节约能源和材料,优化设计方案和加工工艺。传统的设计方法无法满足要求,计算机优化设计的方法可以在设计速度和方案优化上补充传统方法的不足,将机械产品设计的目标和要求通过建模转化为优化设计的目标函数和约束函数,通过计算进行优化的得到设计方案[4]。用优化的方法进行机械产品的设计可以保证设计过程的规范性,设计和校核过程严格按照用户提供的数据库中的要求和公式进行。并且计算机程序也提高了设计的灵活性,当机械产品的设计需要适应新的理念和理论时,用户可以通过更新数据库来快速改进设计方法[5]。
机械优化设计一般属于NP难问题,没有一个确定的方法可以在多项式时间内求解。机械优化问题可以分为机械结构形式的优化、机械结构尺寸参数的优化、机械复杂系统多学科优化等。这些问题可以通过数学模型,将实际问题转化成线性规划、非线性规划和组合优化问题及它们的组合问题,通过优化方法加以求解。但由于机械的设计要综合机电液等多学科,机械产品的对工作性能、安全性能和可靠性等的要求,使得实际的机械优化问题一般具有大规模高度非线性约束,问题的可行解较稀疏,同时由于约束形式多样,通常没有解析式表达的约束。遗传算法只需利用函数值的信息,而无需梯度等高阶信息,因而适用于大规模、高度非线,不连续多峰值的优化以及无解析表达式的优化。遗传算法作为一种群智能优化算法,有很强的鲁棒性和全局收敛性。可以在组合优化和非线性规划中都得到较好的优化效果。
2 基本遗传算法的概述
遗传算法是模拟自然界生物遗传和进化的过程,以群体共同进化的形式搜索一个问题的最优解。群体中每个个体并行的进行适应度评价、选择算子、交叉算子和变异算子等操作并产生新一代个体。
交叉算子模仿自然进化过程中两个同源染色体通过交配而重组产生新的染色体。交叉有一定概率可以结合两染色体的优良基因产生更优的个体,交叉算子是累积优良模式的主要环节。变异算子模拟自然界中基因突变,使复制给新个体的染色体中的基因有一定概率转化为其等为基因。适应度评价算子评价每个个体的表现型求最优解的优良程度,为优胜劣汰提供依据。选择算子是模拟自然界优胜劣汰的过程,以较高的概率保留适应度高的基因,激励好的特性在群体中扩散。选择算子在根据适应度选取的基础上具有一定的随机性,因为选择要容忍一定量的较劣个体的存在以保持种群基因的多样性,保证搜索的全局性,防止算法出现早熟现象。
3 改进小生境变种群规模遗传算法
为使遗传算法对于复杂的约束和目标函数有较好的稳健性和收敛速度,本文介绍了一种带有小生境技术的变种群规模的遗传算法。讨论了种群规模的周期性波动对进化的促进作用,引入了一种新的对约束的处理方法,并改变了选择算子的意义,引入配对算子,规定多父代竞争。整体的程序流程图如图1.
3.1 种群规模波动
传统的遗传算法一般采用固定种群规模。然而自然界中大的生物进化一般都与种群规模的大幅度波动同时发生。生物进化可以分为两个阶段,第一阶段环境稳定种群规模缓慢上升,优良基因逐渐产生与积累;第二个阶段,环境发生灾变种群规模下降,优良基因得到选择并在种群中扩散。改进的遗传算法采用变种群规模规则,种群中个体存活多代,并根据其适应性以某概率被淘汰,存活下的个体按其竞争性依概率交叉配对产生新个体。采用改变约束条件惩罚的苛刻程度的方法使种群规模周期性波动,从而逐步催生优良基因。
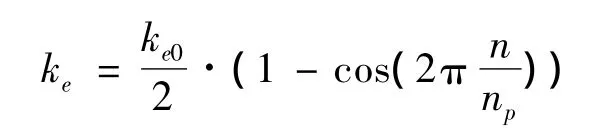
其中ke0为基本惩罚系数,n为进化代数,np灾变周期代数。
3.2 二维小生境
在自然界中,生物一般总和特征相似的生物生活在一起,繁殖后代。又加上地理位置的限制,基因与外界交流得到限制,一个区域的生物群形成一个基因相对独立的小生境。在传统的遗传算法中,选择、交叉算子在整个群体内进行,所有个体的基因交流没有限制,相对优良的基因会很快的在整个种群内扩散,个体很难保持各自的进化方向,整个种群趋于收敛于一个解。故传统的遗传算法很容易出现早熟现象。为改进算法的全局收敛性,引进小生境的概念,将个体的基因交流限制在一个小区域内进行。
设定惩罚苛刻程度的系数为:
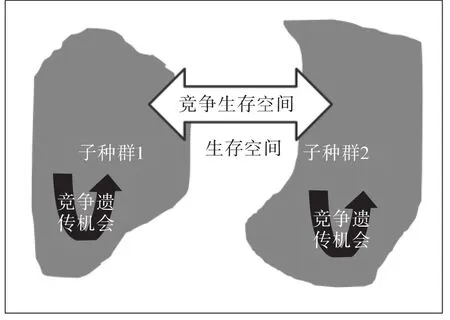
图2 小生境竞争示意图Fig.2 Competition model in Niche environment
如图2所示,在改进的遗传算法中,采用一种位置争夺的小生境技术。将群体投影到一个二维空间。初始种群中个体不会占满全部空间,而是几个个体聚集在一起组成一个初始的子种群,每个子种群之间有一定空间距离。个体在其小生境内进行交叉和配对算子。新生的个体在由母体限定的空间区域内。子种群间会争夺有限的空间,最终使优良基因占有更大空间。
3.3 对目标函数和约束的处理
机械产品的设计要优先考虑满足约束,故机械的优化设计一般为约束优化问题。用遗传算法优化时,处理约束比较常见的方法有如下几种:(1)将不符合约束的个体直接从群体中剔除。(2)采用惩罚函数法,为常用的方法。这种方法要根据不同的约束定义惩罚函数,惩罚函数选取不当将很大的影响优化的收敛速度,或算法很难找到可行解,即使偶然找到,解很差。(3)采用特殊的编码技术,避免产生不满足约束的解,或采用修复技术,但只适用于个别特殊的优化问题。
考虑到在优化设计时以满足约束优先的原则,受到自然界进化机制的启发,将目标函数与满足约束分别用配对和选择两个算子进行搜索。用选择算子淘汰不满足约束的个体,用配对算子挑选下一代个体的父本,使的竞争性高的个体有更大的机会与母本配对。遗传算法在对所有个体进行目标函数和约束的计算评估出适应性和竞争性后,先通过选择算子淘汰部分个体,再从剩余个体中以每个个体为母本,从此个体的一个邻域通过配对算子得到父本,进而进行交叉算子产生新个体。
3.4 编码
在遗传算法搜索过程中,算法不是直接对求解问题的决策变量进行操作,而是通过编码将解空间投射到基因空间,通过交叉,变异对基因进行操作,这是遗传算法的特点之一。
编码是应用遗传算法解决实际问题时要考虑的首要问题,大部分情况下它是影响遗传算法运行效率的主要因素之一。常用的编码方法有:二进制编码法、灰码编码法,浮点数编码法,符号编码法。对于机械优化的问题,设计参数存在尺寸参数等连续值和结构、形状、材料型号等离散量。为保证编码的通用性,采用对离散值和连续值都兼顾的灰码进行编码。
3.5 交叉算子
对于二进制编码的遗传算法,常用的交叉运算方法有单点交叉、双点交叉、均匀交叉等。根据模式理论,为保存优良模式,交叉点选取应越少越好。但如图3所示,单点交叉实际上可以看成是默认以基因段开头与末端为一个交叉点的双点交叉,因此单点交叉对在染色体上不同分布的模式保留的概率不同。故采用模式保留概率稳定的双点交叉算子。
交叉的另一个问题是交叉点的选取。交叉点选取一般的方法为等概率的随机选取。等概率选取交叉点可能存在交叉两片段的基因型相同的情况,则交叉运算后是基因型未改变,降低了交叉效率。故在交叉中剔除相同基因型的交叉,即P{lp=xi|ai=bi}=0.
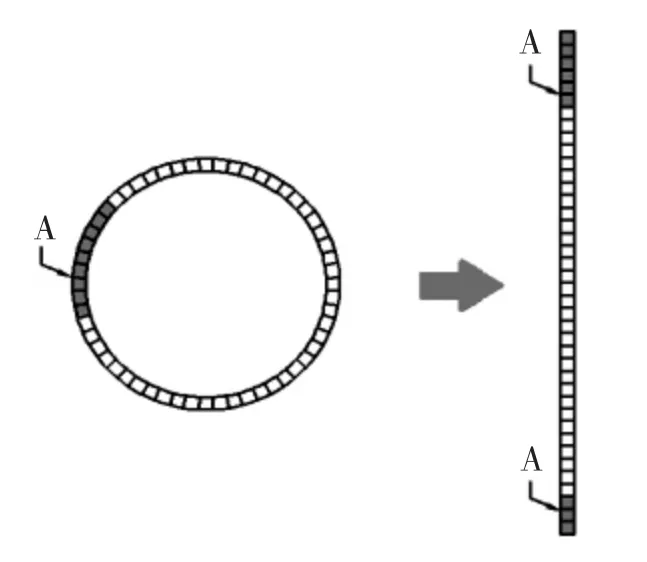
图3 单点叉交隐藏交叉点示意图Fig.3 Extra hidden crossover point in single point crossover method
3.6 变异算子
采用均匀变异算子,对于复制给新个体的每个基因都以父本的变异率变异成其等位基因。变异率会根据个体的适应性在基本变异率的基础上做调整,使得适应性低的个体有较高的变异率。
3.7 选择算子
传统的遗传算法每个个体只生存一代。选择算子的作用是为配对、交叉产生下一代提供父本。选择算子将适应度高的个体有较高的概率遗传到下一代,适应度较低的个体有较低的概率遗传到下一代。
本文提出的遗传算法规定种群的规模是可变的,并且每个个体可以存活一代以上。在改进的遗传算法中选择算子的作用是选择群体中将生存到下一代的个体。根据满足约束的程度计算出适应性,让适应性低的个体有更高的概率被淘汰。选择只保证选择个数的期望为与群体规模成固定比例,个体给选择的概率与个体适应度成正比,本算法的适应度是以满足约束为表征。
其中为总的选择比例的期望。
3.8 配对算子
配对是在基因池中为交叉运算选出一对父母本的过程,是选择算子与交叉算子的中间过程。常用方法是随机配对。本例中的配对是在小生境的范围内进行的,配对的过程中根据个体的竞争性即目标函数值得优劣进行选择。种群中每个存活2代以上的个体在配对算子中都有一次机会作为母本,在小生境的范围内由近到远顺时针选择父本。目标个体被选择为父本的概率与其在小生境内竞争性的排名成正比。
其中rank(A)为个体竞争性排名,mA为子群体内的个体数。
4 实验与结果分析
机械问题的模型可分为连续函数问题和组合优化问题两类。为验证改进的遗传算法的性能并证明其在机械设计中的可行性,做了如下几组实验。首先通过解装箱问题验证变种群对搜索速度的影响,之后通过对比改进的遗传算法、微粒群算法和标准遗传算法在解决装箱问题以及工程实际中的减速箱齿轮组设计和起重机主梁截面设计问题等三个问题的优化结果检验算法的优化性能,验证改进遗传算法的意义。
4.1 种群规模变化对进化的影响实验
此部分采用的实验模型是组合优化中经典的装箱问题。为验证本文提出的种群规模周期性波动有利于促进种群进化的假设,设计改变种群规模波动幅度的实验。通过改变选择算子中的基本惩罚系数ke0来调节种群规模波动的幅度。
本例中按波动从小到大分别进行了三组实验,波动幅度分别为,第一组幅值为0.5;第二组幅值为1;第三组幅值为1.5.上述实验结果均为20次独立重复实验最优个体的目标函数和约束值平均值。实验的结果如图4所示,第二组的优化结果最好,其中有15%能达到最优解4,平均结果为4.85;第三组次之,均能优化到次优解;而波动最小的第一组结果最差,有30%的解只能得到再次优解,平均结果为 5.3.
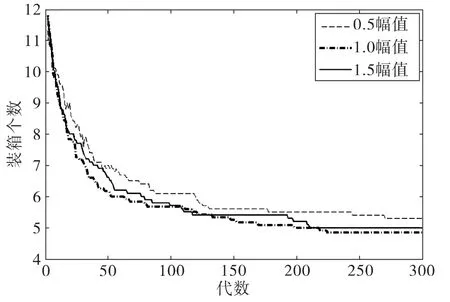
图4 不同波动的结果比较Fig.4 DGA under Different population fluctuation
三组实验的选择比例的平均值均为0.2,只有波动的大小不同。而从实验结果可以看出,种群规模适当的波动可以提高遗传算法的搜索效率和搜索结果,但当波动过大时又会降低搜索结果。可见,种群规模波动对进化具有实际作用。
4.2 改进的遗传算法与其他算法的比较
为验证本文提出的遗传算法的优化性能,以基本遗传算法(SGA)、微粒群算法(PSO)与此处提出的变种群小生境遗传算法(这里简称DGA)做比较。
(1)装箱问题
本单元做了20重物装16箱、50重物装16箱的两组实验。第一组三种算法结果大致相同,第二实验结果如图5所示。可以看出,三种算法虽然搜寻速度大致相同,但改进的遗传算法能得到更优的最优解。
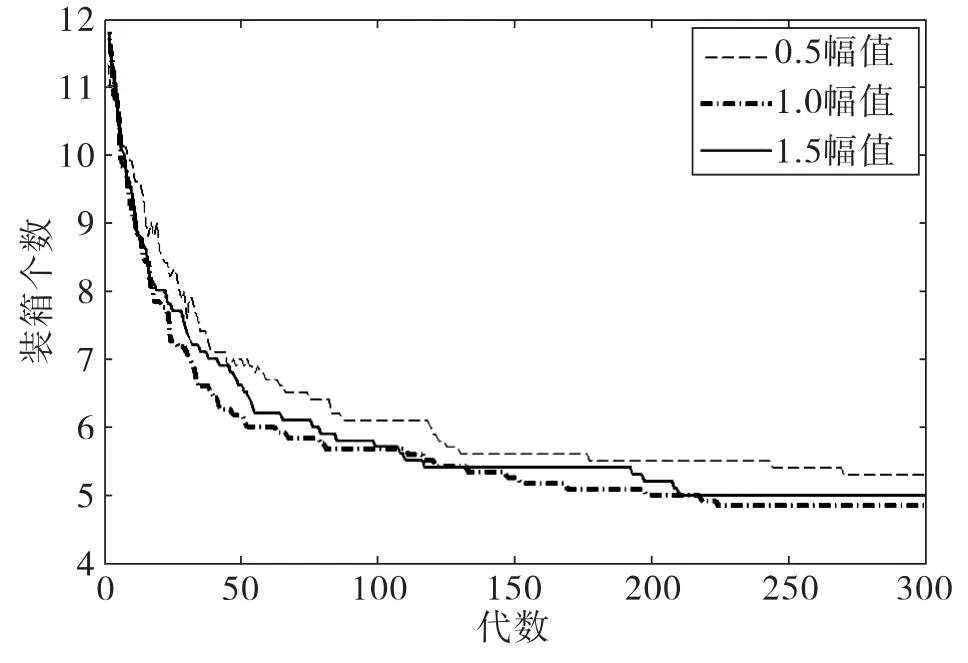
图5 不同算法解装箱问题的比较Fig.5 Different Algorithms to solve packing problem
(2)二级减速器齿轮的优化
本试验采用直尺圆柱齿轮二级减速器的模型,减速器设计条件为高速轴输入功率为6.2 kW,高速轴转速n=1 450 r/min,总传动比i=31.5,齿宽系数φn=0.4;齿轮材料和热处理:大齿轮钢45、正火HB取值范围为187~207,小齿轮钢45、调质HB取值范围为228~255.要求按总中心距最小来确定总方案中的各主要参数。设计变量取为:
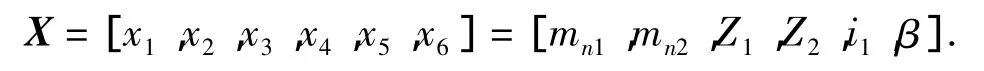
目标函数为中心距最短:
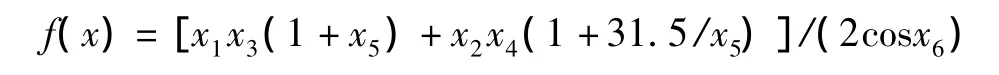
约束有高速机齿轮接触强度条件、低速级齿轮接触强度条件、高速级大齿轮弯曲强度条件、低速级大齿轮弯曲强度条件和大齿轮与轴不干涉条件[6]:
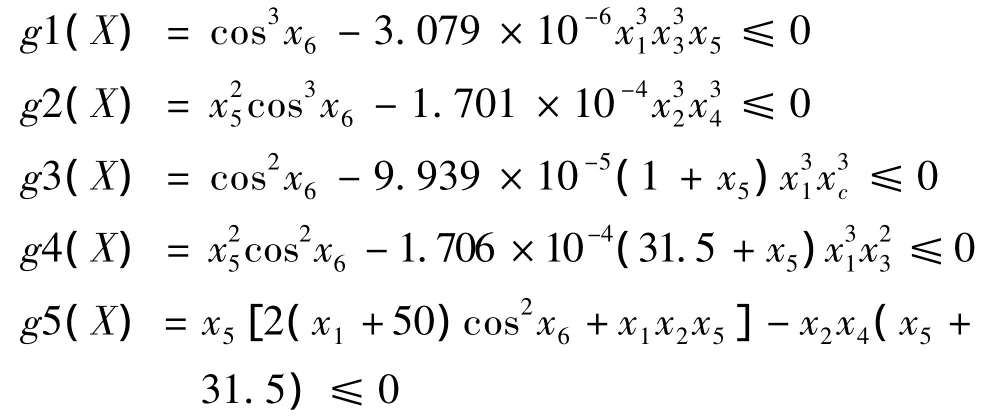
运用三种优化方法,各迭代100代,通过20次重复实验的优化结果如表1:
(3)桥式起重机主梁截面的优化
桥式起重机主梁,以箱形截面为基本结构,取箱形截面的主要尺寸为设计变量,在满足使用性能的要求下,以质量最轻为优化目标,设计变量取为:
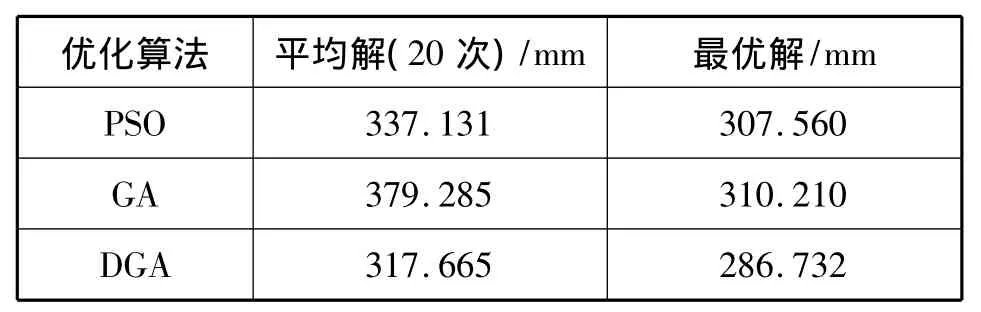
表1 二级减速器齿轮的优化结果Tab.1 Resluts of two-stage helical cylindrical gear reducer
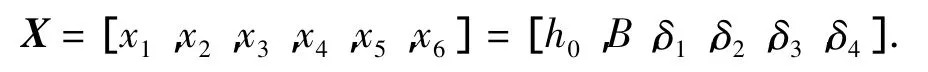
目标函数质量最轻:
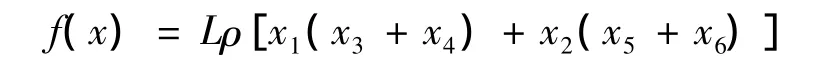
约束有,主梁跨中最大应力约束
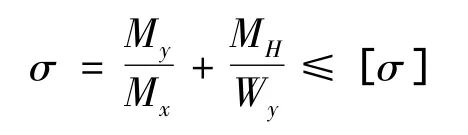
主梁跨端最大剪力约束:τ=τ1+τ2+τ3≤[τ]
静刚度约束:fv≤[fv],fH≤[fH]
动刚度约束:T≤[T]
各板局部稳定性约束:
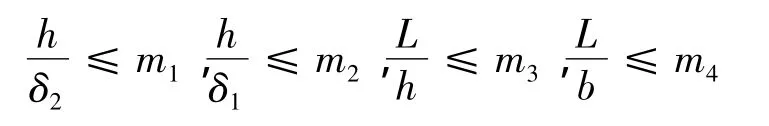
式中m1,m2,m3,m4均按设计规范确定。优化实例取额定起重量t=50 t,跨度为L=35.[7-9]
运用三种优化方法,20次重复实验的优化结果如表2:
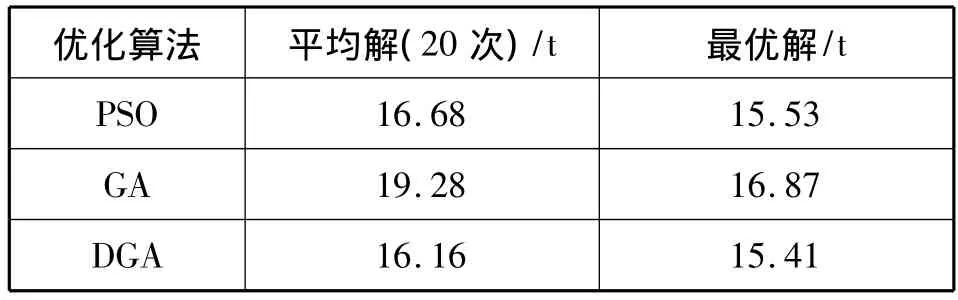
表2 桥式起重机主梁截面的优化结果Tab.2 Results of main beam intersection of bridge crane
5 结束语
遗传算法是对自然界的生物遗传进化的模拟,但是传统的遗传算法在种群规模、交叉繁殖和个体更替等方面的模拟过于简化,实际上弱化了每个个体在群体进化中能起的作用,使得遗传算法很难在解决复杂的问题时保持算法的稳定性,很难收敛于最优解。
本文介绍的遗传算法是对机械设计问题具有一定通用性的优化方法。针对其目标函数和约束的类型不单一,规模较大的特点,将约束和目标函数并列处理。此方法相对于常用的惩罚函数法,提高了算法在种群进化中对约束和目标的规模相对变化的适应性。本文提出了一种新的以二维的种群空间为基础的加入小生境技术和种群规模波动理念,个体多代生存,细化配对、选择算子的遗传算法模式,对个体行为更加细致的模拟在较小的额外计算支出的前提下更大限度的利用了每一个搜索点的信息。并通过几组实验初步验证了其可行性、展示了其优良性能,但此遗传算法模式的实用性以及针对具体的复杂问题的稳定性以及执行效率仍有待进一步的研究。
[1]俞琚.中国工程机械行业的发展现状、前景和主要问题[J].建筑,2011(22):15-17.
[2]玄光男,程润传.遗传算法与工程设计[M].北京:科学出版社,2000.
[3]郭永强.CAD技术介绍[J].太原科技大学学报,2006,27(S0):107-108.
[4]周明,孙树栋.遗传算法原理及应用[M].北京:国防工业出版社,1999.
[5]董立立,赵益萍,梁林泉,等.机械优化设计理论方法研究综述[M].机床与液压,2010,38(15):114-118.
[6]IOANNIS G.TSOULOS.Solving constrained optimization problems using a novel genetic algorithm[J].Applied Mathematics and Computation,2009(208):273-283.
[7]俞鸿斌.二级圆柱齿轮减速器优化设计及其MATLAB[J].实现装备制造技,2007(5):36-41.
[8]陶元芳,董辉强,黄朝辉.双梁门式起重机可视键控优化设计[J].太原重型机械学院学报,2001,33(1):18-20.
[9]李杨,卫良保.基于VC和MATLAB的单梁起重机主梁优化设计[J].太原科技大学学报,2012,33(1):27-29.
