一种特征向量正交的MI MO阵列多目标检测方法

贾继鹏，王 亮

（中国人民解放军91245部队，辽宁 葫芦岛 125001）

一种特征向量正交的MI MO阵列多目标检测方法

贾继鹏，王 亮

（中国人民解放军91245部队，辽宁 葫芦岛 125001）

正交波形MIMO雷达各阵元发射相互正交的信号波形，利用波形分集虚拟扩展阵列孔径，提高阵列系统自由度，采用低增益的宽波束照射探测空域从而获得比相控阵雷达更加优越的检测和估计性能.利用信号子空间和噪声子空间特征向量的正交性，提出MIMO阵列特征向量检测技术(EDT)多目标检测方法(MIMO-EDT)，突破了传统相控阵列EDT方法只能检测小夹角目标的限制，并与常规阵列算法作比较，通过计算机仿真说明MIMO-EDT方法多目标检测能力优于传统相控阵EDT方法.

多输入多输出；协方差；特征门限法；参数估计；目标检测

本文研究基于协方差矩阵特征分解的MI MO阵列多目标检测方法，根据信号子空间和噪声子空间特征向量的正交性，提出MIMO阵列特征向量检测技术(EDT)多目标检测方法(MI MO-ED T)，突破了传统相控阵列ED T方法只能检测小夹角目标的限制，对目标夹角较大时也能有效估计目标数目，而且还分析了目标初始方位角对MI MO阵列ED T方法性能的影响，并与传统相控阵列目标回波信号存在相关性情况下的多目标检测性能作了比较.

1 阵列输出信号协方差矩阵特征分解模型

假定MIMO阵列系统采用一个均匀线列阵，该均匀线列阵由N个阵元组成，相邻阵元间隔为d，所有N个阵元都可用于接收信号，均匀间隔地选取其中的M个阵元作为发射阵元（M≤N），相邻发射阵元间隔为d，M个发射阵元发射彼此正交的窄带信号{Sm(t)},m=1,2,…,M.假定在阵列远场存在K个目标，则所有M个阵元发射信号经K个目标反射后，所有N个接收阵元上的阵列输出信号可表示为

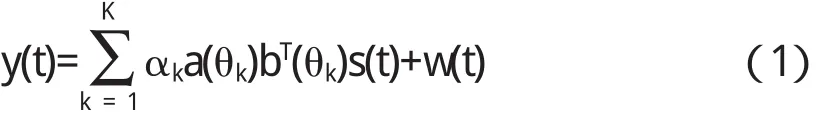
式中 θk表示第 k个目标方位，b(θ)=表示M个发射阵元构成的发射阵列的阵列流形向量，a(θ)=表 示N个接收阵元构成的接收阵列的阵列流形向量，w(t)表示n个接收阵元上的噪声，αk表示第k个目标的反射系数，是确定未知的变量.为简单起见，假定MIMO阵列发射窄带正交信号，发射信号与噪声不相关，噪声是均值为零，方差为的白噪声，且各阵元上噪声彼此独立.

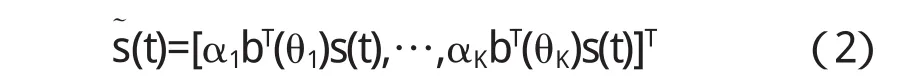
其中α=ding(α1,α2,…,αK)，B(θ)=[b(θ1),b(θ2)…b (θK)]表示发射阵列流形矩阵，A(θ)=[a(θ1)a(θ2)…a(θK)]表示接收阵列流形矩阵，则“等效目标源”信号模型下MIMO阵列输出信号可改写成如下形式

MIMO阵列输出信号自相关矩阵如下

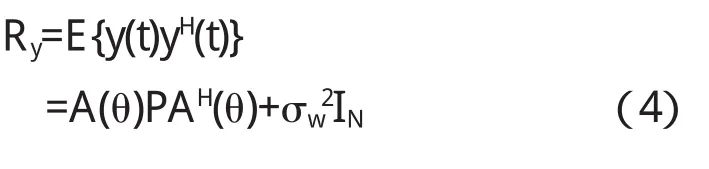
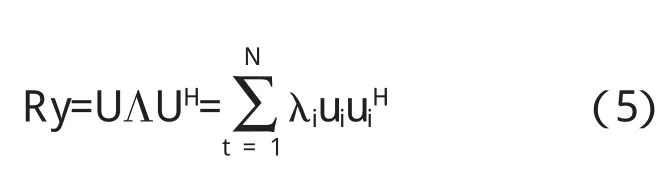
其中Λ=diag(λ1,λ2,…,λN)是由特征值构成的对角矩阵，且特征值满足

ui是与特征值λi对应的特征向量.K个目标情况下，(5)式可改写为

其中Λs是前K个大特征值组成的对角矩阵，Us是与大特征值对应的特征向量构成的矩阵，称为信号子空间，Λw为后N-K个小特征值构成的对角矩阵，Uw是与小特征值对应的特征向量构成的矩阵，称为噪声子空间，信号子空间和噪声子空间正交.

工程上Ry无法精确得到，对MIMO阵列输出信号采样，则MIMO阵列输出采样协方差矩阵近似估计为

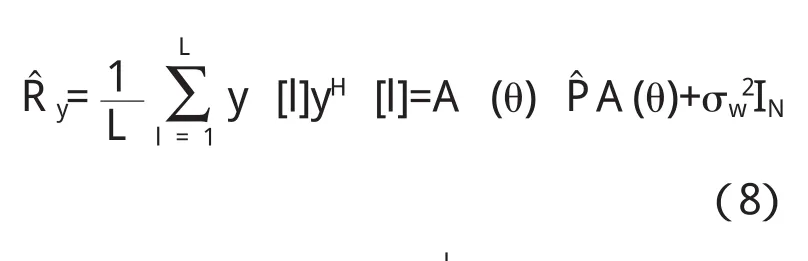
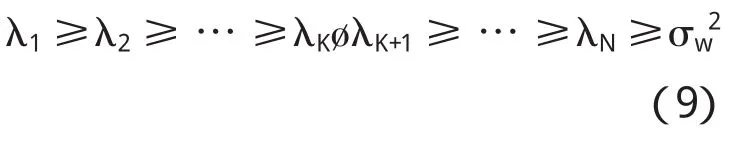
2 MIMO-EDT方法

MIMO-ED T方法利用信号子空间和噪声子空间的正交性检测目标个数.MI MO阵列输出采样协方差矩阵R^y如（8）式分解，其中AP^AH的非零特征值为λ'1≥λ'2≥…≥λ'Q，R^y的N个特征值λ1≥λ2≥…≥λN对应的特征向量分别为u1,u2,…，uN，令u→1,u→2,…，u→N为MIMO阵列特征向量u1,u2,…，uN在Δθ→0时的极限值，它可由下列矩阵：

其中τ为选定的门限值.当ui与信号有关时，ηi大于或等于门限τ，就认为在θ0附近发现了一个目标信号，否则没有目标信号，当i从1到N-1变化时，MI MO-ED T方法检测到的目标个数为发现目标信号的次数.

3 性能分析

对提出的MI MO阵列ED T方法的多目标检测性能进行统计分析，研究多目标检测方法对单目标和双目标的正确检测概率以及最低可检测信噪比等性能，并分别与传统相控阵列目标检测性能相比较，这里假定了传统相控阵列目标回波是完全不相关的.

仿真模型：假定MIMO阵列由10个阵元按半波长（载波频率处）等间隔均匀布放，收发共用（M=N=10），发射窄带正交波形，载波频率f0=5 kHz，采样频率fs=30 kHz，快拍数为2000，统计次数为200.信噪比定义为针对单个目标的阵元输出信噪比，且存在多目标时假设多个目标具有相同目标反射系数.

按（10）式选取MIMO-ED 方法的检测门限.假定单目标方位为0°，在取不同值条件下，MIMO-法检 T方法单目标的正确检测概率与传统相控阵EDT方法的正确检测概率如图1所示；两目标方位分别为-5°和5°（夹角为相控阵列一个波束宽度）时，在门限τ取不同值条件下，MIMO-EDT方法双目标的正确检测概率与传统相控阵EDT方法的正确检测概率如图2所示.图1表明，传统相控阵EDT方法与MI MO-EDT方法具有几乎相同的单目标检测能力；但对于目标方位夹角较大的情况（10°），传统相控阵EDT方法失效，无法检测双目标，而MIMO-EDT方法依然能有效检测双目标，如图2所示，说明了MIMO-EDT方法大夹角多目标检测能力优于传统相控阵列；此外，τ值的不同（检测门限的选取）在一定程度上会影响MIMO-EDT方法和相控阵列EDT方法的检测性能，对高信噪比和低信噪比检测性能折中，文中取τ=0.5.

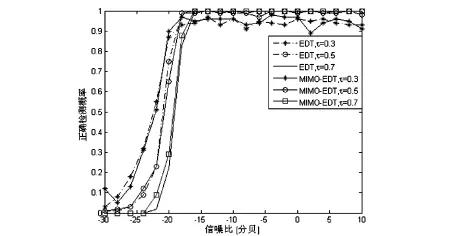
图1 取不同值时MI MO-EDT方法与EDT方法单目标检测性能对比

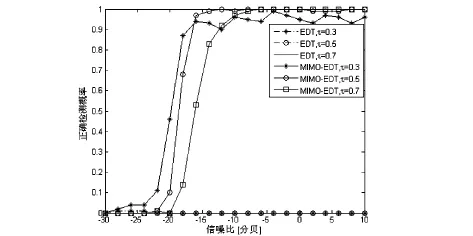
图2 取不同值时MI MO-EDT方法与EDT方法双目标检测性能对比

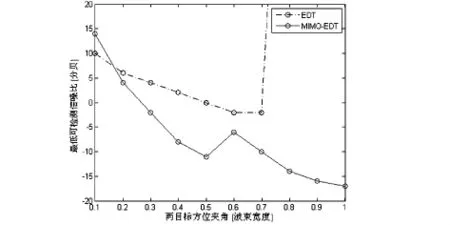
图3 目标夹角取不同值时MI MO-EDT方法与EDT方法双目标检测性能对比（τ=0.5）

图3给出了MIMO-EIT方法对两目标夹角取不同值时的最低可检测信噪比，并与传统相控阵EDT方法进行了比较.从图3上可以看到，双目标夹角分别在1°至5°之间和6°至10°之间时，MIMO-EDT方法双目标最低可检测信噪比随目标夹角的变大而逐渐降低，然而，目标夹角变化从5°（半波束宽度）到6°时，MIMO-EDT方法双目标最低可检测信噪比发生了跃变，但仍然小于传统相控阵双目标最低可检测信噪比，从而说明了M IM O-法目 T方法双目标检测性能始终优于传统相控阵EDT方法，值得注意的是，当目标夹角极小（1°）时，MI MO阵列ED T方法目标检测性能略低于传统相控阵列ED 方法.

4 结论

本文提出的MIMO阵列EDT方法，并给出了计算机仿真结果，通过计算机仿真，基于MI MO阵列ED T算法比传统相控阵EDT算法相比，可以检测出目标方位夹角较大多目标，并且双目标检测性能优于传统相控阵EDT方法.MI MO阵列EDT方法有着良好的应用前景.

〔1〕Wax M and Kailath T, “Detection of Signals by Information TheoreticalCriteria”,IEEE Trans.on Acoustics,Speech,and Signal Processing[J].vol.33,pp.387-392,1985.

〔2〕Wax M and Ziskind I., “Detection of the NumberofCoherentSignalbytheMDL Principal”,IEEE Trans.on Acoustics,Speech, and SignalProcessing [J].vol.37,pp. 1190-1196,1989.

TN 957

A

1673-260X（2013）02-0015-03