含逆向物流的电子易逝品库存控制及仿真

马向国

（北京物资学院物流学院，北京市 101149）

一、引言

近年来，随着经济的发展和人们生活水平的提高，社会对电子产品的需求量日益猛增，电子行业拥有巨大的销售市场和乐观的发展前景。然而，电子产品更新换代的时间越来越短，对于制造商和销售商来说，如何科学合理地控制库存，是在这场竞争中能否胜出的一个关键点。

电子易逝品是指具有一定销售时间限制的电子产品，过了一个时间点t，若还没有销售出去，则产品对于这段销售时间和销售市场将会失去其价值。随着科技的快速发展，高科技电子产品更新速度很快，其显著的特点就是生命周期显著缩短和价值急剧衰减，例如芯片、手机、电脑等。[1]

无论是从技术的角度还是市场的角度来说，电子产品作为库存可以在仓库存放的时间是相当有限的，特别是那些高技术含量的易过时产品，但现有研究并没有对其隐含条件进行深入挖掘，缺少过期产品对整个存在退货的库存控制系统影响的研究。

二、含逆向物流的电子易逝品制造商库存控制模型

1.问题描述

电子产品经销售流向用户，由于产品瑕疵或者质量问题造成回收物流，这些回流的电子产品经过检测，有一部分可以经过核心部件的升级改造（再制造），进入可服务产品库存，然后重新返回销售市场。可服务产品库存包括新制造的产品和再制造的产品。在可服务产品库存中，因为电子产品的易逝性，需要对每件产品标识它的“年龄”，对于超过销售时间限制的产品，要从库存系统中剔除。制造商库存系统如图1所示，库存的增加既包括制造量P，也包括再制造量R，而外界对产品的需求和过期产品的剔除使得库存减少。

2.模型的假设

（1）研究一个单再制造周期，多个制造周期的单一产品库存系统，在一个周期内包括一个再制造周期和n个制造周期。

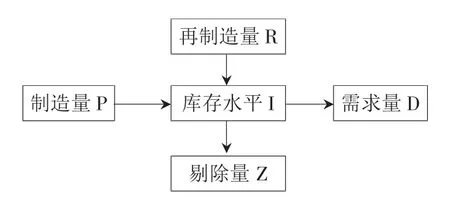
图1 制造商库存系统

（2）市场对电子产品的需求是稳定且连续均匀的，即需求速度为d的常数，产品的回收率和再制造率是确定且连续的，分别为λ、r。

（3）为了规避缺货风险，最小库存水平为Q0。假设当需求变为原来的2倍，再制造周期结束时，库存量可以满足市场需求。

（4）电子产品的生命周期为L，在每个周期内对可服务电子产品进行连续检查，将超出生命周期的产品从库存中剔除，剔除率为z。

（5）生产能力、再制造能力、生产准备成本、库存持有成本均为常数，产品市场价格随时间呈线性递减。再制造能力、需求率均大于回收率（r>λ，d>λ），制造能力、再制造能力均大于需求率和剔除率之和（p>d+z，r>d+z）。

（6）全部回收产品可用于再制造，经再制造后进入可服务产品库存，且质量、价格与新产品无差异。

3.模型参数及变量说明

在本模型中涉及到众多参数和变量，如产品价格、需求率、制造率、回收率、库存持有成本等等。模型参数及变量说明如表1所示。

4.模型建立与求解

在实际生产中，回收品的量比较小，而且为了防止回收品放置时间过长，在每个循环周期中，先进行一次再制造生产，再启动制造生产，并且有若干次制造生产，过程如图2所示。

T1：再制造生产过程，产量为QR，回收品库存以r-λ的速度递减。在此期间，制成品库存以r-d-z的速度递增。T1结束时，回收品库存为0，制成品库存为T1（r-d-z）+Q0。因为在T1时间内再制造率是r，再制造量是 QR，故有 T1=QR/r。

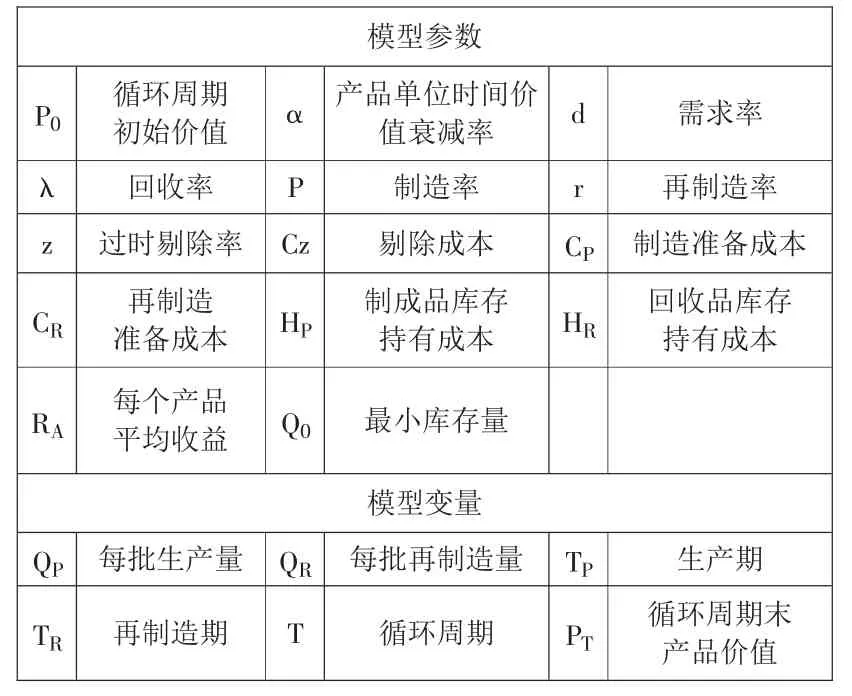
表1 模型参数及变量说明

T2：制成品库存以d+z的速度减少，T2结束时，减少到Q0。由于当需求变为原来的2倍，再制造周期结束时，库存保有量和再制造量能满足市场需求，故有（2d+z）TR=QR+Q0，即：

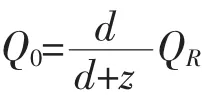
T3：制造生产过程，制成品库存以p-d-z的速度递增。在T3时间段内产量为QP，故有T3=QP/p。T3结束时，制成品库存为T3（p-d-z）+Q0。

T4：制成品库存以d+z的速度减少，T4结束时，减少到Q0。

再制造周期：

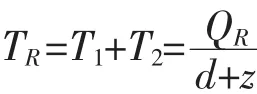
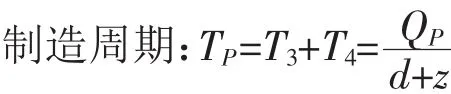
每个周期内所有回收产品用于再制造，所以：

又因为每个周期内全部产品用来满足市场需求和库存剔除，所以有：

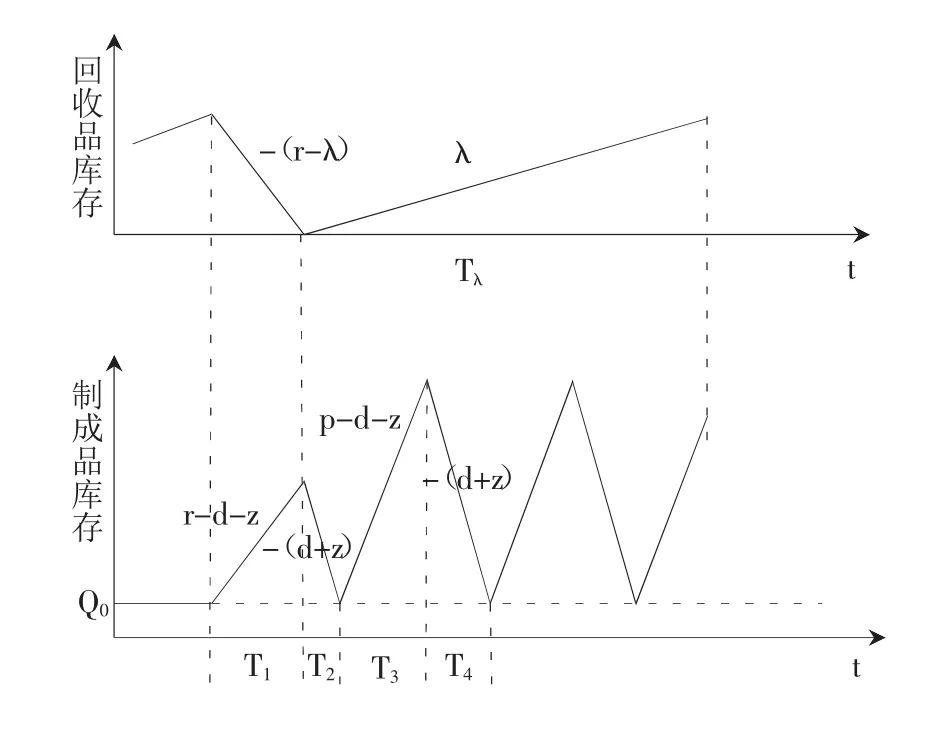
图2 库存水平变化过程

回收品库存为：

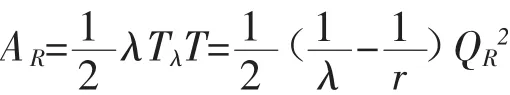
制成品库存为：

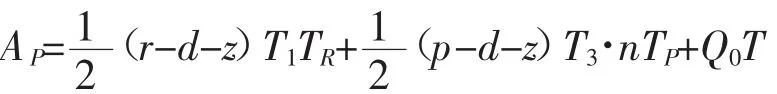
总成本为：

C=nCP+CR+zTCz+ARHR+APHP

由于电子产品的易逝性，一个循环周期后，价格由之前的P0衰减为PT=P0-αT，总收益为：

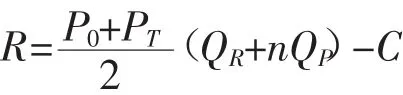
每个产品的平均收益为：

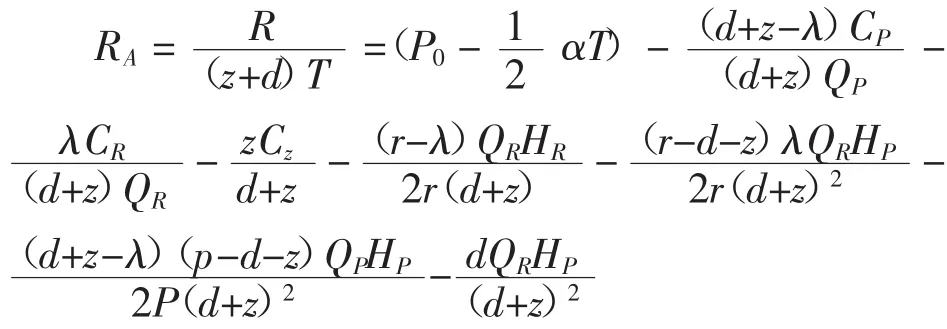
要使每个产品的平均收益最大

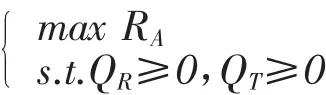
解上述有约束的最优化问题：

由于该规划为凸规划，且目标函数为严格凸函数，Kuhn-Tucker条件是其最优点存在的充要条件，故求其K-T点即可得到最优解：[2]

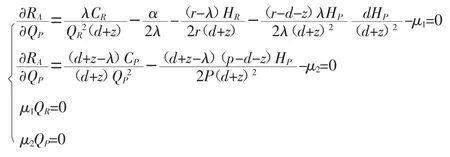
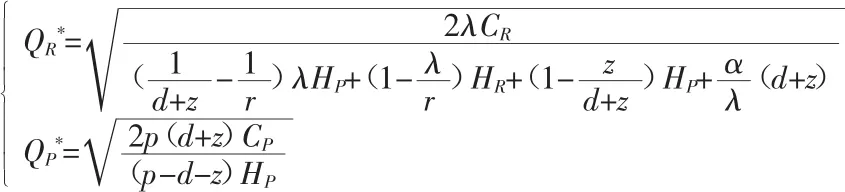
令u1-u2=0，得最优再制造批量和制造批量：

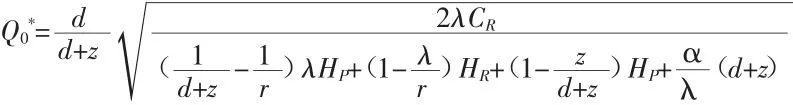
从上面两式中可以看出，电子产品最佳再制造量受回收率、再制造率、需求率、剔除率、价值衰减率的影响，而最佳制造量仅与生产率、需求率和剔除率有关。回收率和再制造量决定了一个循环周期的长短，而每个周期内制造的次数又由制造量和周期的长短决定。随着价值衰减率α的增大，最佳再制造量和库存保有水平都会降低，以此来防止周期过长、库存保有水平过高使产品的价值大幅度衰减。同时，库存时间过长的产品会从库存中剔除，所以减小每个周期的制造量来降低库存量，是减少过期产品的有利途径。

基于以上两点可以得到，易逝性电子产品的库存量不宜过高，然而，库存量的降低会增加启动制造的次数，增加生产准备成本，而且又会导致顾客服务水平的下降，所以寻求库存成本和制造启动成本以及库存水平和顾客服务水平的平衡点是接下来需要继续探讨的问题。

三、含逆向物流电子易逝品制造商库存仿真与优化

1.仿真软件Arena介绍

Arena是美国系统建模公司（System Modeling）于1993年开始基于仿真语言SIMAN及可视化环境CINEMA研制开发的可视化互交集成式商业化仿真软件。[3]作为通用的可视化仿真环境，Arana的应用范围十分广泛，几乎可以覆盖可视化仿真的所有领域。在物流领域，Arena的应用涉及从供应商到客户的整个供应链，包括供应商管理、库存管理、制造过程、分销物流、商务过程及客户服务等。利用Arena的图形建模与分析模块，可以构建出不同的仿真模型，并可以根据实际需要设定仿真参数进行动态系统模拟，从而对实际的复杂系统进行有效分析和处理。

2.仿真模型需要解决的问题

在EOQ模型中定性分析了电子产品易逝性对库存控制的影响。在此仿真模型中，根据某电子产品制造商历史制造数据得到产品需求率、库存剔除率、生产率等相关信息，以EOQ数学模型为基础，利用仿真软件Arena建立仿真模型。

在实际生产中，制造商可以控制和改变每个周期内的制造量和再制造量，从而改变总成本。在此模型中，总成本包括存储成本、制造和再制造准备成本、剔除成本。如果在每个周期内制造量和再制造量比较小，在一段时间内启动次数多，它的生产准备成本就会很高。当然，库存成本就会降低。通过对制造量和再制造量的优化设计，寻求二者之间的最优组合，得到产品平均成本最低是此次仿真的最终目标。

3.仿真模型设计

根据数学模型和仿真流程图，以一个电子产品制造商为例，建立一个基于随机需求的制造商库存控制系统的仿真模型。

本模型模拟的是一个周期内，在需求和制造都随机变化并有剔除情况存在的前提下，回收品库存和可服务产品库存的变化情况，并由此计算出总成本和平均成本。变量和参数设置如表2所示。

4.仿真实验及结果分析

设置每个周期内再制造量是300，制造量是500，系统运行每个周期的时间是360天，共运行3个周期。经过调试，运行仿真模型，可服务产品库存水平变化过程如图3所示。

运行结束，查看仿真报告，得到总成本和平均成本，如表3所示。3个运行周期平均总成本是428433元，产品平均成本是1184元。

根据模型运行结果数据可得，在QR=300，QS=500，运行周期是360天的情况下，总成本是428433元，平均成本是 1184元。当改变（QR，QS）组合，相应的存储成本和生产准备成本会随之改变，进而影响总成本，可以利用Arena优化工具来寻求（QR，QS）的最佳组合，使平均成本达到最小。

5.利用 OptQuest模块寻求最优（QR，QS）组合

OptQuest是Arena一个外部集成的优化工具，它具有强大的分析功能来为仿真模型寻求最佳的解决方案。[4]可以用来定义系统输入（如控制变量与约束变量）和期望的系统输出（如目标函数），然后指导系统对输入的每一组变量进行筛选，通过计算目标函数以得到最佳的输出。

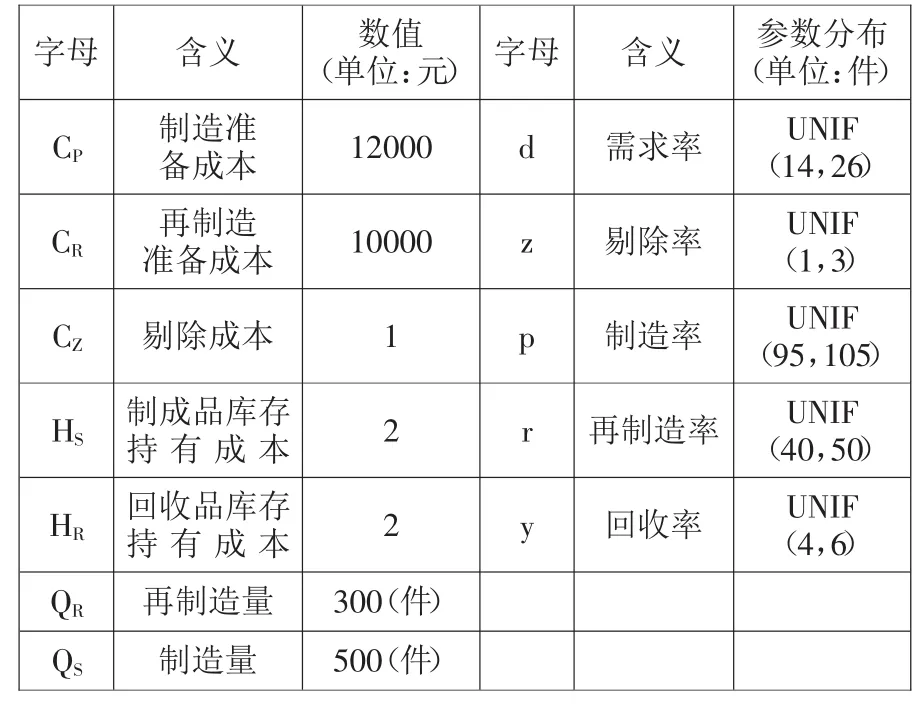
表2 变量和参数设置

在本仿真模型中，需要通过OptQuest工具寻求最佳制造量和再制造量，以达到使总成本最小、平均利润最大的目标。打开OptQuest优化工具后，在控制变量项中选择QR和QS作为控制变量并将QP-QS>0作为约束条件，在目标函数选项卡中选择Minimize Objective使Average Total Cost最小作为目标函数。运行模型，寻优过程与最优解如图4所示，最终得到：当QR=220，QP=790时，平均成本最小，为 930。

OptQuest优化工具的优势显而易见，在此模型中，它能够对一定范围内所有的制造量和再制造量作为输入来计算平均成本，直至找到最小平均成本值，它可以指导企业对库存控制系统作出最佳决策，进而为生产计划的制订提供依据。[5]

四、总结

图3 可服务产品库存

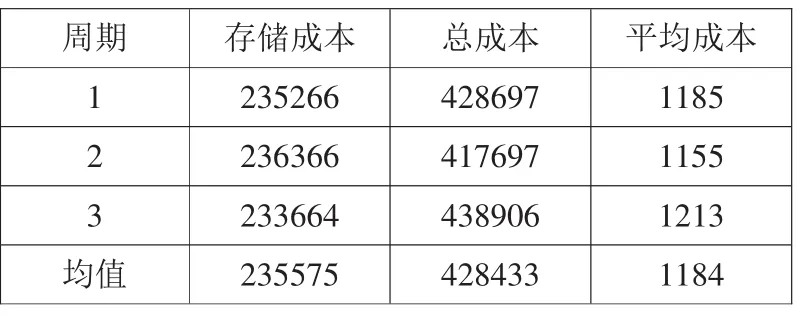
表3 仿真运行结果

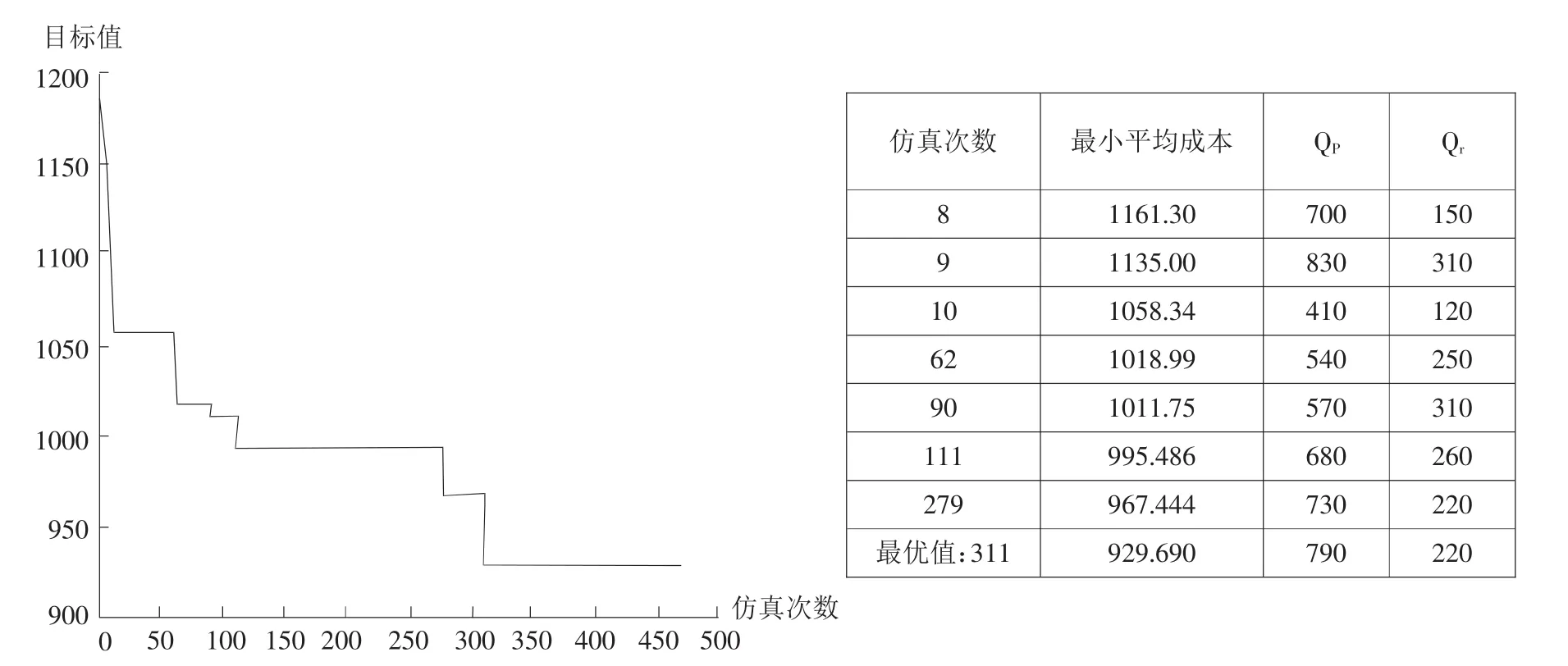
图4 寻优曲线与最优解

本文是对含逆向物流的电子易逝品库存控制的研究，针对电子产品生命周期短、价值衰减迅速的特点，设置产品剔除率和价值衰减系数，建立库存控制数学模型，推导出最优制造批量和再制造批量以及最小库存水平。在现实条件下，各种不确定因素随时发生，数学解析法在很多情况下无所适从，然而利用Arena仿真软件对模型进行模拟仿真，便使此问题迎刃而解，而且可以通过优化工具对模型进行优化，使得制造商寻求到最佳制造策略和库存策略，以达到平均成本最小化的目标。

[1]包宁.易逝性高科技产品更新过程风险的未确知测度评价[J].科技管理研究，2007（3）：180-183.

[2]杜仕斌.电子产品的回收物流库存控制研究[J].上海管理科学，2006（4）：75-77.

[3]周海荣.离散制造企业生产物流系统建模与仿真[D].成都：西南交通大学，2010：45-55.

[4]陈志卷.三鹿奶粉物流系统分析与库存策略仿真[D].天津：河北工业大学，2007：48-50.

[5]曾敏刚.废旧电子类产品的逆向物流研究[J].科技管理研究，2006（8）：60-63.