裂缝性储层射孔井水力裂缝张性起裂特征分析
2013-07-31任岚赵金洲胡永全王磊
任岚,赵金洲,胡永全,王磊
(西南石油大学 油气藏地质及开发工程国家重点实验室,四川 成都,610500)
水力裂缝起裂压力计算对水力压裂优化设计具有重要的作用和影响,该问题也是水力压裂理论研究的重点难点问题。最早的起裂压力计算模型都是针对均质地层裸眼井建立的[1-2]。随着完井技术的发展,人们开始关注射孔井的起裂压力计算,常将射孔孔眼看作一个小的裸眼井与井筒相连,考虑水力裂缝沿孔眼壁面起裂[3-4]。近年来,随着斜井钻成,对斜井破裂压力研究成为新的焦点[5-8]。上述起裂压力计算模型都是针对均质地层,基于以上起裂压力计算理论,井眼壁面只存在2个对称的起裂方位,形成的水力裂缝为关于井眼对称的平面双翼裂缝。然而,最新研究表明,在裂缝性储层中,水力裂缝常常扩展为多分支非平面的缝网[9-13],表现为复杂的起裂和扩展模式。为此,开展裂缝性储层水力裂缝起裂理论研究对认识裂缝性储层水力裂缝起裂特征和延伸规律具有十分重要的理论价值和现实意义,本文作者考虑水力裂缝沿天然裂缝张性起裂,建立了裂缝性地层射孔井张性起裂压力计算的理论模型,利用该模型计算分析水力裂缝沿天然裂缝张性起裂压力变化规律,从而认识裂缝性储层的水力裂缝起裂特征。
1 地质物理模型
首先建立裂缝性储层射孔井水力裂缝沿天然裂缝起裂压力计算的地质物理模型,作如下假设:(1) 天然裂缝性地层为射孔完井,天然裂缝面与射孔孔眼随机相交;(2) 天然裂缝处在主发育带上,具有相同的走向和倾向;(3) 考虑天然裂缝为非充填的张开性裂缝,水力裂缝较容易沿天然裂缝张开起裂;(4) 不考虑套管与水泥环之间胶结程度对起裂的影响。基于以上假设条件,可得裂缝性地层射孔井起裂压力计算的地质物理模型如图1所示。
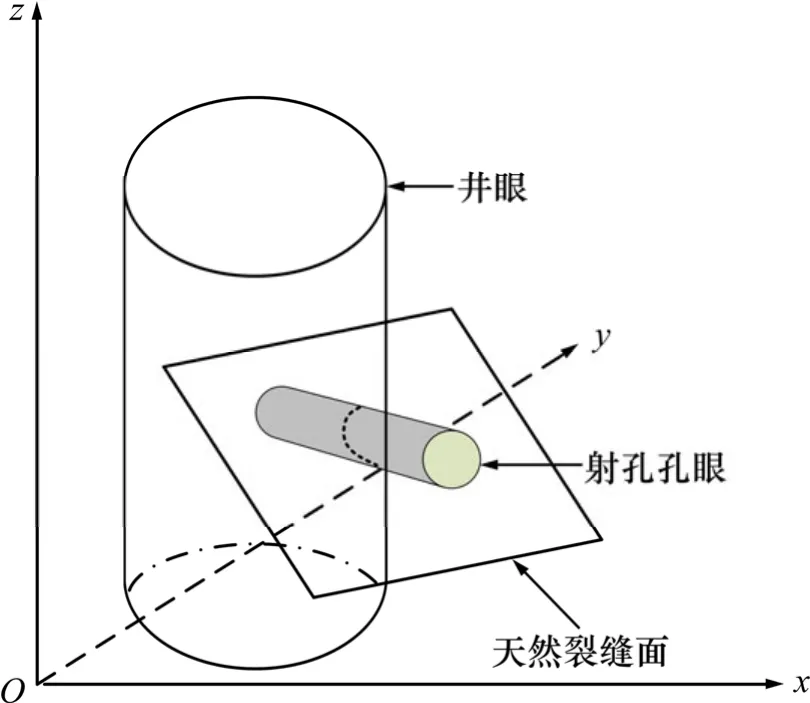
图1 天然裂缝与射孔孔眼相交的地质物理模型Fig.1 Geophysics model for intersection between natural fracture and perforated tunnel
2 井眼围岩应力分布
井眼围岩应力场是计算射孔孔眼壁面应力分布的前提,受固井质量的影响,水泥环与地层岩石之间往往存在微小的裂隙,水力压裂时压裂液很容易流入这些微小裂隙中,导致井底流体压力直接作用在地层岩石上,因此,射孔井围岩需要考虑受远场地应力和井底流体压力的联合作用[14],定义张应力为负,压应力为正,井眼围岩所受的应力在极坐标系下表示为:
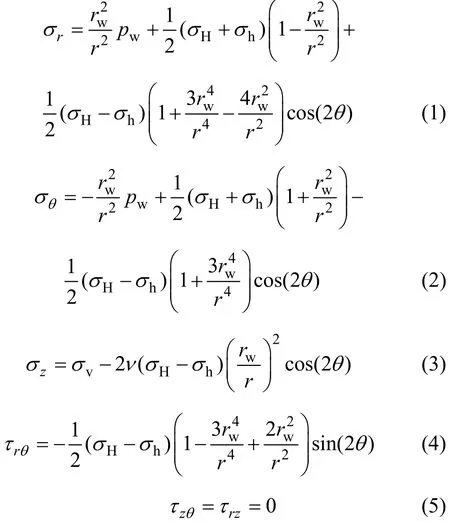
式中:σH为水平最大地应力,MPa;σh为水平最小地应力,MPa;σv为上覆地层压力,MPa;σr为径向应力,MPa;σθ为周向应力,MPa;σz为垂向应力,MPa;τrθ为剪切应力,MPa;pw为井底流体压力,MPa;rw为井眼半径,m;r为应力计算点井眼极坐标半径,m;ν为泊松比;θ为径向上水平最大地应力方向逆时针旋转的极坐标角,(°)。
3 孔眼壁面主应力计算
孔眼壁面三维主应力是计算水力裂缝沿天然裂缝张性起裂压力的基础。为了计算孔眼围岩的应力分布,可将射孔孔眼看作一个小的裸眼井与井筒相连[3-4],在空间上受到3个方向应力作用,分别为水平方向上应力σθ、垂直方向上应力σz和孔眼轴向上应力σr,孔眼围岩受力如图2所示。
考虑孔眼围岩像井筒围岩一样的应力集中[15],在井底流体压力和孔眼围岩应力作用下,考虑压裂液的渗流效应,孔眼壁面围岩所受的应力状态可在射孔孔眼极坐标系中用径向应力σs、周向应力σφ、轴向应力σzz及相应剪切应力表示:
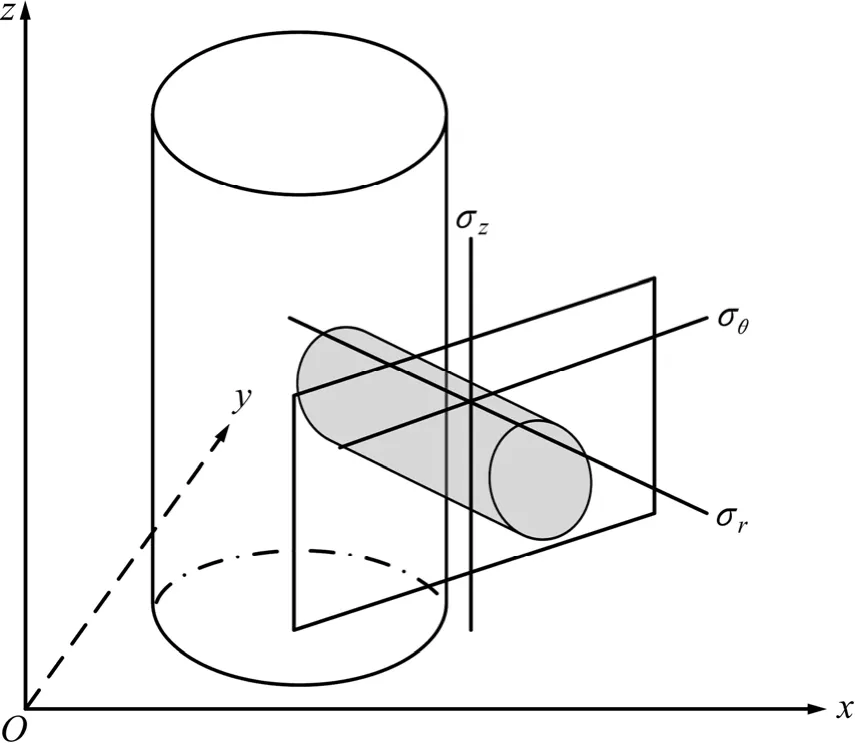
图2 射孔孔眼围岩受力示意图Fig.2 Diagram of stresses acting on rock around perforation
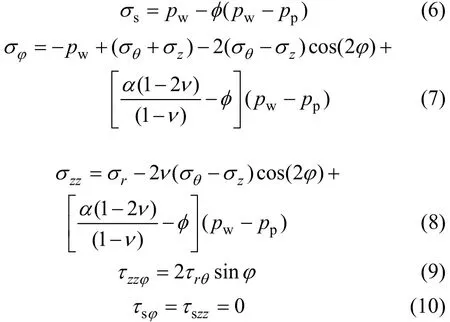
式中:pp为孔隙流体压力,MPa;φ为地层孔隙度,无因次;α为有效应力系数,无因次;φ为孔眼上主应力σθ方向逆时针旋转的极坐标角,(°)。
式(6)~(10)组成了孔眼壁面上任意点的三维应力场,由于其中τsφ和τszz为 0,则σs为其中的一个主应力,而切向应力τzzφ不为 0,因此,周向应力σφ和轴向应力σzz不是φ-zz平面的主应力,φ-zz平面的主应力可以通过复合应力理论进行计算,很容易得到孔眼壁面上任意点的3个主应力为:
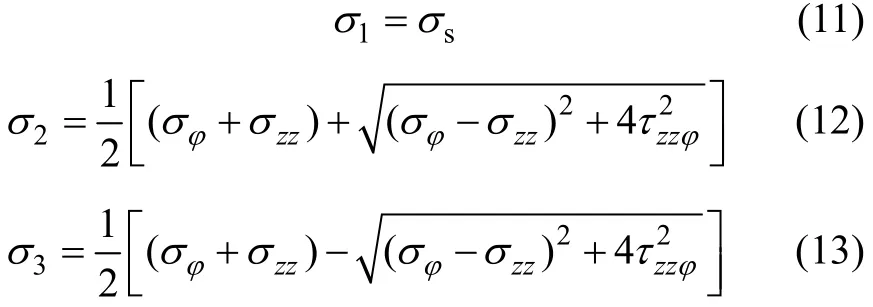
事实上,主应力σ2和σ3是2个相互垂直应力σφ和σzz在φ-zz平面内旋转一定的角度γ得到,旋转的角度γ正好使得的剪切力τzzφ等于0。由平面复合应力理论可知,平面应力转换计算的旋转角度γ满足以下方程:
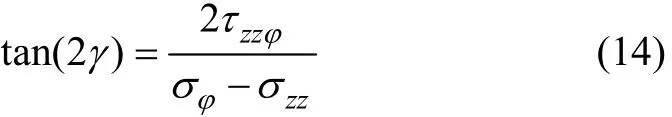
求解该方程,可得满足该方程存在2个可能解:
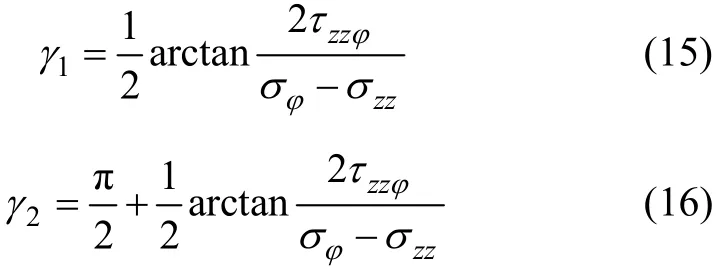
容易看出γ1和γ2是φ-zz平面内2个主应力的方向,但角γ与主应力σ的对应关系如何,还需进一步的分析。为了确定主应力与旋转角度的对应关系,引入最大拉伸应力判别的极值函数[7]:
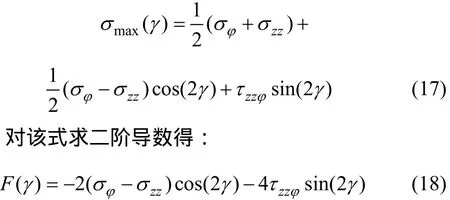
由于F(γ1)和F(γ2)的符号相反,但必有一个是F>0,而另外一个是F<0。可以很容易证明,使得F>0的γi为较大的主应力σ2与应力σzz的夹角。
4 沿天然裂缝张性起裂压力计算模型
如果天然裂缝与孔眼相交,在井底流体压力增加过程中,天然裂缝内的流体压力也将增加,当天然裂缝内的流体压力不小于天然裂缝所受的有效压应力时,水力裂缝沿天然裂缝张性起裂:

式中:pf为天然裂缝内流体压力,MPa;σn为作用在天然裂缝面上的正应力,MPa。
在已知孔眼壁面天然裂缝受到的三维主应力,可计算天然裂缝受到的正应力为:

式中:βi为天然裂缝面法线与主应力σi的夹角,(°)。
为了计算作用在天然裂缝上各个主应力与天然裂缝面法线夹角的余弦。首先要已知天然裂缝与孔眼之间的相对位置关系,考虑在大地坐标系(N,E,Sky)中,假设天然裂缝的走向为北偏东角度Ne,天然裂缝倾角Dip,水平最大地应力方位为北偏东角度Ha,孔眼方位为水平最大地应力σH方向为起点旋转角度θ,天然裂缝与孔眼壁面相交点为主应力σθ方向为起点旋转角度φ。以此假设条件,对天然裂缝的法线方向矢量和各个主应力的方向矢量进行计算。
根据假设条件,可得到在大地坐标系中天然裂缝面法线的方向矢量为:
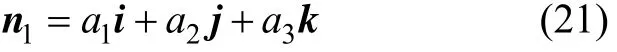
式中:a1=-sinDipcosNe;a2=sinDipsinNe;a3= cosDip。
根据上述假设条件,孔眼壁面的主应力在地应力坐标系中的空间位置关系如图3所示。由图3中主应力σ1的空间方向,结合坐标变换原理[16],可推导在大地坐标系下σ1的方向矢量为:
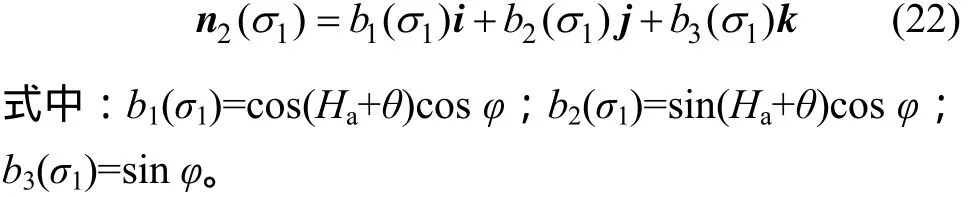
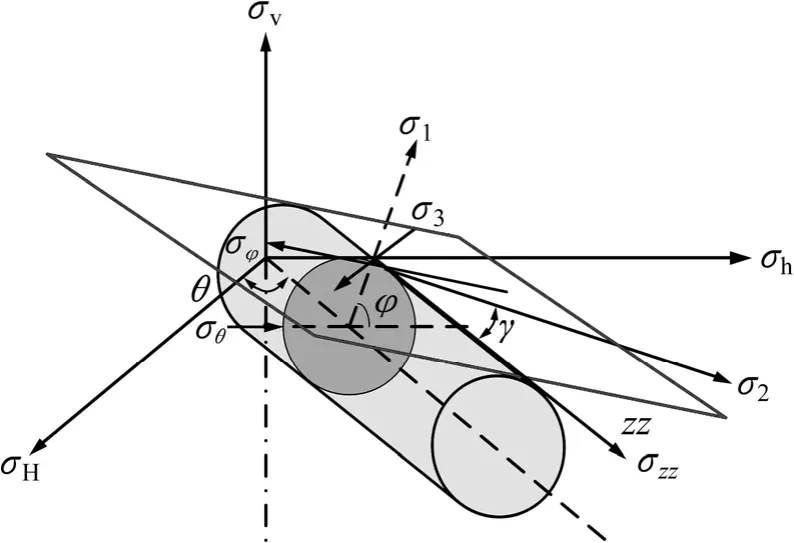
图3 射孔孔眼壁面主应力在地应力坐标系中的空间位置关系Fig.3 Spatial relationship of principal stresses of perforation wall in geostress coordinate system
同理,很容易推导在大地坐标系下σ2的方向矢量为:

同理,很容易推导在大地坐标系下σ3的方向矢量为:
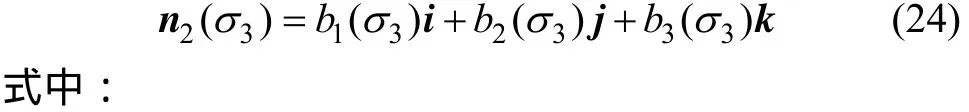
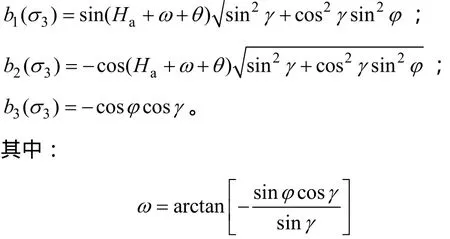
由式(21)~(24)可得天然裂缝面法线方向与各个主应力σi方向的夹角余弦为:
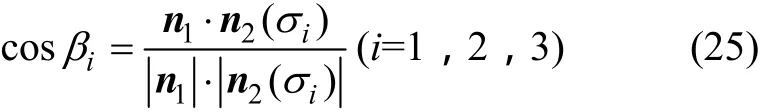
将式(11)~(13)和式(25)代入式(20)可得到作用在天然裂缝面上的正应力,再代入式(19)就可判断水力裂缝是否沿天然裂缝张性起裂。由于孔眼壁面主应力是作用点位置和井底流体压力的函数,不能直接得到张性起裂压力表达式,因此,可以采用井底流体压力逐步升高的试算法进行求解,采用适当的井底压力上升速率步长,一旦给定的井底压力满足张性起裂判别式(19),表明在该井底流体压力下,水力裂缝将沿天然裂缝发生张性起裂。
5 计算与分析
基于以上起裂压力计算模型和计算方法,以东部某盆地裂缝性储层实际数据为例,如表1所示,以此分析裂缝性地层射孔井的张性起裂压力变化规律和起裂特征,然后基于实例井压裂施工作业数据对起裂压力计算模型进行验证。
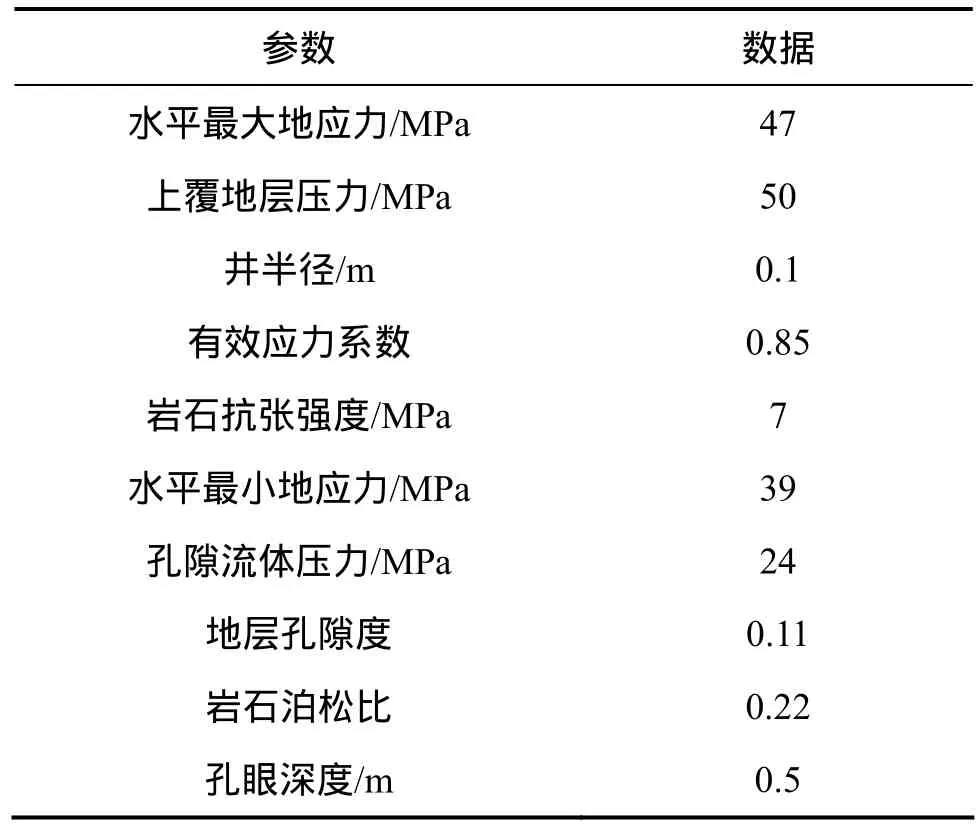
表1 张性起裂压力计算基本数据Table 1 Data for calculation of tensile initiation pressure
5.1 起裂压力规律及起裂特征分析
水力裂缝总沿起裂压力最小的位置起裂,为此,对于特定孔眼方位,定义岩石本体起裂压力为张性起裂发生的门限值,如果张性起裂压力低于岩石本体起裂压力,认为水力裂缝沿天然裂缝张性起裂,否则沿岩石本体起裂。为了对比张性起裂的发生,对均质地层射孔井岩石本体起裂进行计算[1-2],可得水平最大地应力方位和水平最小地应力方位岩石本体起裂压力为39.5 MPa和64.9 MPa。可见:均质地层的水力裂缝将沿水平最大地应力方位起裂延伸。
5.1.1 孔深对起裂的影响
假设孔眼位于水平最大地应力方位,天然裂缝相交孔眼顶部位置,天然裂缝走向北偏东 70°,天然裂缝倾角60°。图 4所示为张性起裂压力随天然裂缝与孔眼相交深度位置的变化规律。从图4可见:受井眼周向应力集中和孔眼轴向应力变化影响,随孔眼深度的增加,起裂压力先增加后减小,最小张性起裂压力位于孔眼指端处。在整个孔眼深度上张性起裂压力都较岩石本体起裂压力低,在孔眼指端处的张性起裂压力较本体起裂压力39.5 MPa降低了36.2%。
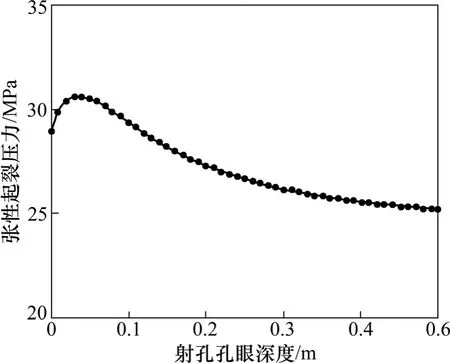
图4 张性起裂压力随孔眼深度的变化Fig.4 Changes of tensile initiation pressure with perforation depth
5.1.2 孔眼周向位置对起裂的影响
孔眼位于水平最大地应力方位(θ=0°),天然裂缝相交孔眼周向的顶部位置(φ=90°)。图5所示为该位置天然裂缝倾角和走向对张性起裂压力的影响。由于该孔眼方位岩石本体起裂压力为39.5 MPa,从图5可见:在低倾角或者中高走向情况下,张性起裂压力小于岩石本体起裂压力,水力裂缝将沿天然裂缝张性起裂。孔眼位于水平最大地应力方向上(θ=0°),天然裂缝相交孔眼周向的水平位置(φ=0°)。图6所示为该位置天然裂缝倾角和走向对张性起裂压力的影响。对比图6和图5可见:该位置张性起裂压力总体上说较相交在孔眼顶部位置(φ=90°)要高,由于该孔眼方位岩石本体起裂压力为39.5 MPa,则相交在该位置的天然裂缝能发生张性起裂的走向和倾角范围极小。为此,天然裂缝与孔眼相交点的孔眼周向角越大,张性起裂压力越小,越容易沿天然裂缝张性起裂,天然裂缝相交孔眼顶端位置的张性起裂压力最小。
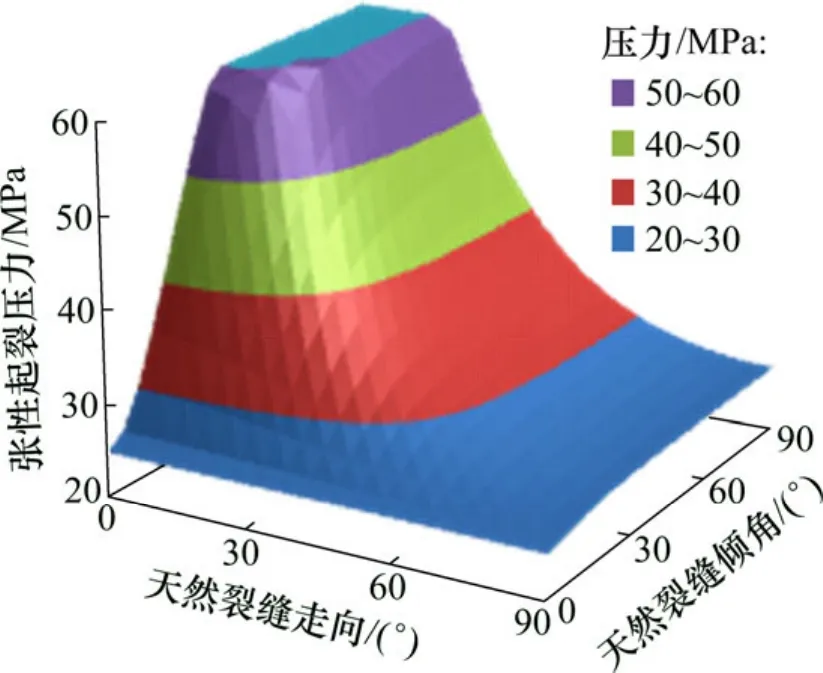
图5 不同天然裂缝走向和倾角下的张性起裂压力Fig.5 Variation of tensile initiation pressure under different strike and dip of natural fractures
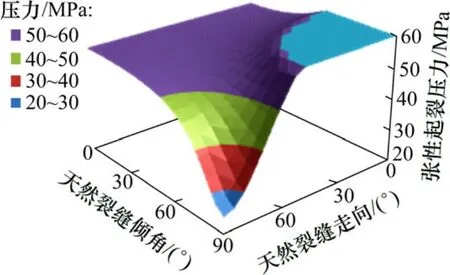
图6 不同天然裂缝走向和倾角下的张性起裂压力Fig.6 Variation of tensile initiation pressure under different strike and dip of natural fractures
5.1.3 水平应力方位对起裂的影响
孔眼位于水平最小地应力方位上(θ=90°),天然裂缝相交孔眼的顶部位置(φ=90°)。图7所示为天然裂缝倾角和走向对张性起裂压力的影响。由于该孔眼方位岩石本体起裂压力为64.9 MPa,从图7可见:该位置天然裂缝在任意倾角和走向下都会发生张性起裂。对比图5和图7可见:天然裂缝为低倾角时,水平最大地应力和水平最小地应力方位的水力裂缝张性起裂压力都在20~30 MPa区间内,这时2个方位的起裂压力差变小,井眼周向上的等效起裂点增多,这种作用效应将导致水力裂缝从井眼周向不同方位的孔眼同时起裂延伸,产生径向缝网。
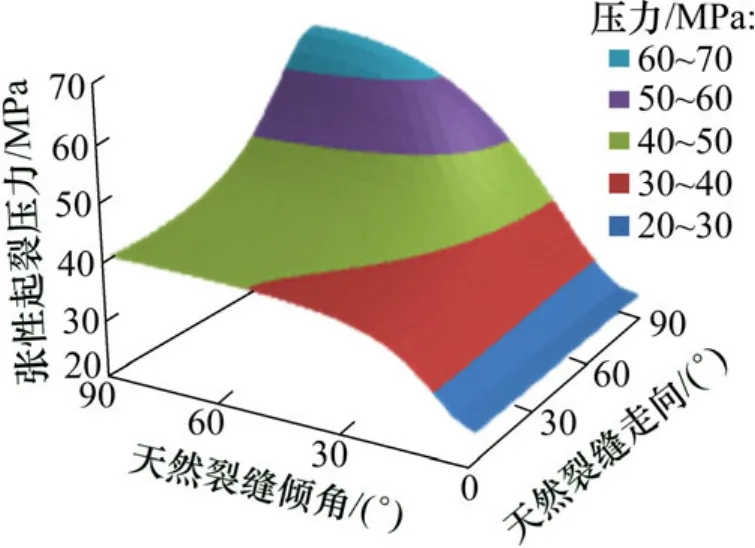
图7 不同天然裂缝走向和倾角下的张性起裂压力Fig.7 Variation of tensile initiation pressure under different strike and dip of natural fractures
5.2 模型验证分析
以该盆地B59-68井进行模型验证分析,施工层段1 994.8~2 013.0 m;储层水平最大地应力方向为北偏东72°;天然裂缝走向为北偏东45°;天然裂缝倾角为20°。储层假设为均质地层的起裂压力为 39.5 MPa,而测试压裂得到该井实际起裂压力为29.2 MPa,远小于岩石本体起裂压力,为此,水力裂缝为沿天然裂缝起裂。采用文中建立的张性起裂压力模型,计算得到水平最大地应力和水平最小地应力的水力裂缝张性起裂压力分别为30.56 MPa和30.1 MPa,模型计算值的相对误差为3.1%,在工程误差范围内,证实了本文起裂压力计算模型的可靠性。
模型计算得到 2个极端方位的起裂压力差仅为0.46 MPa,为此判断水力压裂时水力裂缝将可能从井眼不同方位起裂延伸。根据该井压裂施工过程水力裂缝延伸的微地震监测结果,绘出了裂缝延伸分布如图8所示。由图8可见:近井水力压裂充分发育,延伸方位分别为北偏东 58°~75°,北偏西 15°以及北偏西28°,近井地带具有径向缝网的扩展特征,证实了理论模型对该井水力裂缝沿不同孔眼方位同时起裂延伸推断的正确性。
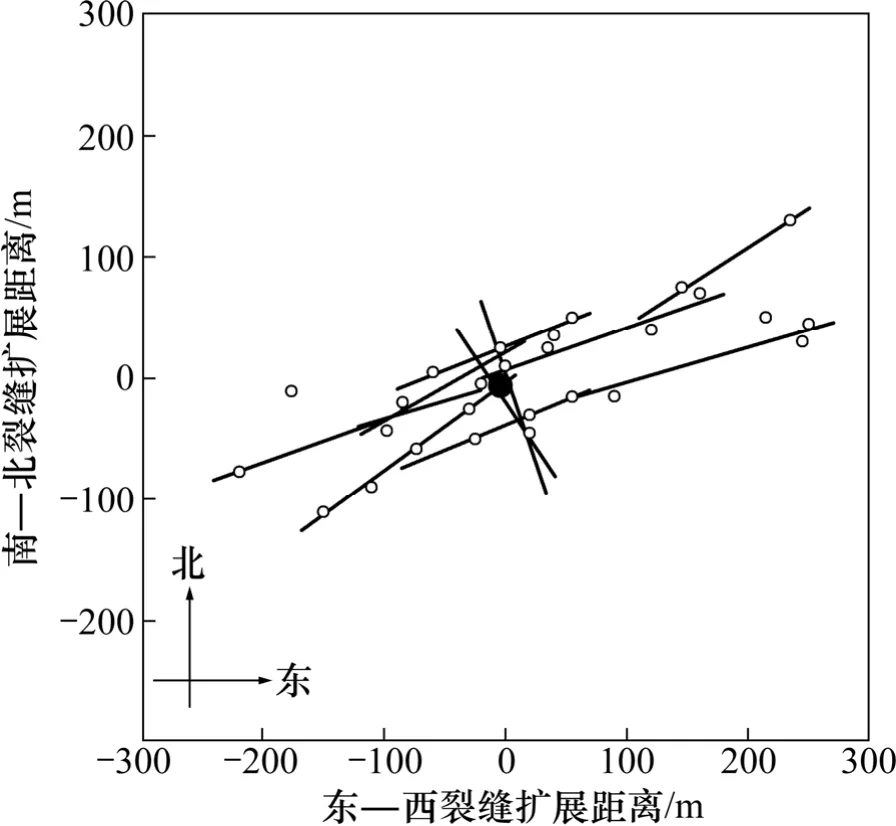
图8 微地震监测的水力裂缝扩展方位分布Fig.8 Distribution of hydraulic fractures based on microseismic monitoring
6 结论
(1) 基于孔眼壁面与天然裂缝相交点受到的主应力以及孔眼与天然裂缝之间的相对位置关系,建立了裂缝性地层射孔井水力裂缝沿天然裂缝的张性起裂压力计算模型,该模型可用于裂缝性地层压裂时水力裂缝张性起裂压力计算和近井裂缝扩展模式分析。
(2) 水力裂缝沿天然裂缝张性起裂压力受天然裂缝与孔眼壁面相交位置、孔眼在井眼周向上的方位以及天然裂缝走向和倾角多种因素的影响,裂缝性储层具有比均质地层起裂压力低,水力裂缝容易沿天然裂缝起裂;同时井眼周向不同方位上存在多裂缝同时起裂延伸的显著特征。
(3) 实例计算证实了文中起裂压力模型计算精度高、计算结果可靠,该模型为裂缝性地层压裂优化设计提供了相应的理论依据,具有重要的理论价值和现实意义。
[1]Hubbert M K, Willis D G.Mechanics of hydraulic fracturing[J].Transactions of Society of Petroleum Engineers of AIME, 1957,210∶ 153-168.
[2]Haimson B, Fairhurst C.Initiation and extension of hydraulic fractures in rocks[J].SPEJ, 1967, 7(3)∶ 310-318.
[3]刘翔.垂直射孔井地应力及破裂压力研究[J].钻采工艺, 2008,31(2)∶ 36-38.LIU Xiang.Study on earth stress and fracturing pressure in vertical perforated wells[J].Drilling & Production Technology,2008, 31(2)∶ 36-38.
[4]Fallahzadeh S H, Shadizadeh S R, Pourafshary P.Dealing with the challenges of hydraulic fracture initiation in deviated-cased perforated boreholes[R].SPE 132797, 2010.
[5]Yew C H, Li Y.Fracturing of a deviated well[J].SPE Production Engineering, 1988, 3(4)∶ 429-437.
[6]Hossain M M, Rahman M K.Hydraulic fracture initiation and propagation∶ Roles of wellbore trajectory, perforation and stress regimes[J].Journal of Petroleum Science and Engineering, 2000,27∶ 129-149.
[7]陈勉, 陈治喜, 黄荣樽.大斜度井水压裂缝起裂研究[J].石油大学学报, 1995, 19(2)∶ 30-35.CHEN Mian, CHEN Zhixi, HUANG Rongzun.Hydraulic fracturing of highly deviated wells[J].Journal of China University of Petroleum, 1995, 19(2)∶ 30-35.
[8]罗天雨, 郭建春, 赵金洲, 等.斜井套管射孔破裂压力及起裂位置研究[J].石油学报, 2007, 28(1)∶ 139-142.LUO Tianyu, GUO Jianchun, ZHAO Jinzhou, et al.Study on fracture initiation pressure and fracture starting point in deviated wellbore with perforations[J].Acta Petrolei Sinica, 2007, 28(1)∶139-142.
[9]Mahrer K D.A review and perspective on far-field hydraulic fracture geometry studies[J].Journal of Petroleum Science and Engineering, 1999, 24(1)∶ 13-28.
[10]陈勉, 周健, 金衍, 等.随机裂缝性储层压裂特征实验研究[J].石油学报, 2008, 29(3)∶ 431-434.CHEN Mian ZHOU Jian, JIN Yan, et al.Experimental study on fracturing features in naturally fractured reservoir[J].Acta Petrolei Sinica, 2008, 29(3)∶ 431-434.
[11]Fisher M K, Heinze J R, Harris C D, et al.Optimizing horizontal completion techniques in the Barnett shale using microseismic fracture mapping[R].SPE 90051, 2004.
[12]Soliman M Y, East L, Augustine J.Fracturing design aimed at enhancing fracture complexity[R].SPE 130043, 2010.
[13]East L, Soliman M Y, Augustine J.Methods for enhancing far-field complexity in fracturing operations[R].SPE 133380,2010.
[14]陈勉, 金衍, 张广清.石油工程岩石力学[M].北京∶ 科学出版社,2008∶ 168-169.CHEN Mian, JIN Yan, ZHANG Guangqing.Rock mechanics of petroleum engineering[M].Beijing∶ Science Press, 2008∶168-169.
[15]郭建春, 辛军, 赵金洲, 等.酸处理降低地层破裂压力的计算分析[J].西南石油大学学报∶ 自然科学版, 2008, 30(2)∶ 83-86.GUO Jianchun, XIN Jun, ZHAO Jinzhou, et al.The calculation analysis of decreasing formation fracturing pressure by acidizing pretreatment[J].Journal of Southwest Petroleum University∶Science and Technology Edition, 2008, 30(2)∶ 83-86.
[16]黄宣国.空间解析几何[M].上海∶ 复旦大学出版社, 2004∶41-44.HUANG Xuanguo.Spatial analytic geometry[M].Shanghai∶Fudan University Press, 2004∶ 41-44.
