卧式双轴搅拌槽的液固两相流数值分析

严宏志，李新明，吴波，徐海良

(中南大学 高性能复杂制造国家重点实验室，湖南 长沙，410083)

卧式双轴搅拌设备广泛应用于机械、化工、冶金等领域，搅拌效率的提高以及设备磨损的减少是搅拌设备的设计关键。目前，卧式双轴搅拌的设计主要依赖经验，难以预测搅拌性能。近年来，利用计算流体力学(CFD)研究搅拌槽内的流动及混合特性逐渐受到重视，在立式单轴搅拌方面国内外学者采用数值模拟方法已开展不少研究，如：Micale[1]用欧拉模型分析搅拌槽内中低质量分数的固体颗粒的分散；Montante等[2]对搅拌槽内颗粒的分布进行模拟；Jaworkski等[3]对搅拌槽的混合效率进行研究；Kasat等[4]模拟搅拌槽的液固两相混合；Taghavi等[5]研究双桨涡轮搅拌槽的功耗；Dohi等[6]研究搅拌槽在气液固三相中的能耗，侯拴弟等[7]利用 k−ε湍流模型分析搅拌槽在不同工况下的速度场分布；钟丽等[8]对液固两相流颗粒离底悬浮进行数值模拟研究；王乐勤等[9]模拟分析三层搅拌槽的混合过程。本文作者利用数值模拟仿真的方法分析卧式双轴搅拌槽在不同工况下的流场特性对搅拌功率的影响，并研究不同工况下的叶片磨损率，以便为提高搅拌效率降低叶片磨耗提供依据。

1 流场数学模型的建立

液固两相流除把流体视为连续介质外，把颗粒群视为拟流体，流体流动受质量守恒(连续方程)、动量守恒、能量守恒，当流动处于湍流状态还应遵守湍流运输方程[10]。在直角坐标系下微分形式连续性方程，动量方程(N−S方程)如式(1)和(2)所示。

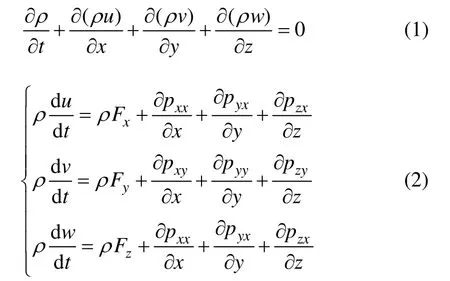
其中：ρ为密度；u，v和w为3个坐标轴方向的速度分量；Fx，Fy和Fz分别是单位质量流体上的质量力在3个方向上的分量；Pij为流体内的应力张量的分量(i=x，y，z；j=x，y，z)。

2 计算过程

通过Pro/E软件设计流场的几何模型，搅拌器包含2个搅拌轴，叶片呈螺旋布置，叶片螺距为180 mm和240 mm 2种，每个螺距内5个叶片，流场模型如图1所示。几何模型导入GAMBIT中划分网格[11]，由于搅拌叶轮是多层螺旋式，流场区域不规则选用非结构化四面体网格，对于流动变化大的区域和叶片处网格加密，设定不同的流域及边界条件，网格划分如图2所示。模拟采用耦合非稳态求解器，定义多相流为Eulerian模型，湍流模型为RNG k−ε，采用无滑移边界条件和标准壁面函数，定义流体物理性质第一相为液体水，第二相为颗粒需要用户自定义属性(密度、粒径、黏度等)，设定边界条件：入口为速度入口边界，出口为自由出口边界，搅拌轴为旋转壁面边界，其余为固定壁面，最后求解并进行后处理[12]。

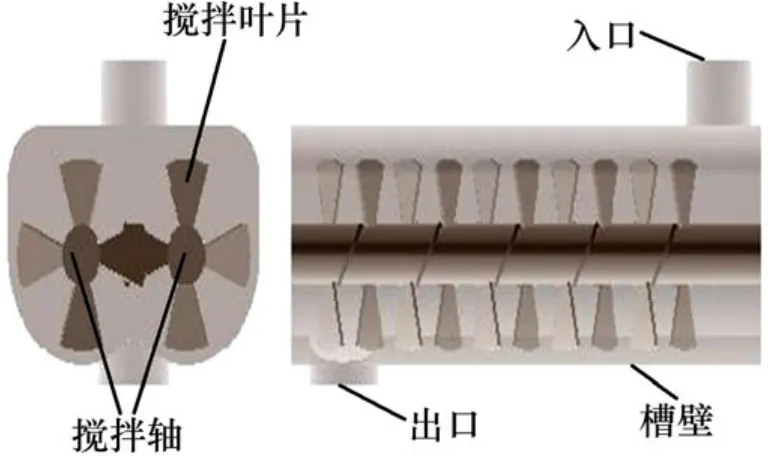
图1 搅拌槽几何模型Fig.1 Geometry model of stirred tank

图2 搅拌槽网格模型Fig.2 Mesh model of stirred tank

3 仿真结果分析

在不同工况下分析搅拌槽的速度场，压力场，湍流强度以及颗粒运动轨迹对搅拌功率及叶片磨损的影响，7种不同的工况如表 1所示。表 1中：N1和 N2分别是2个搅拌轴的转速；v1和v2分别是液相、固相的入口速度；d为颗粒直径；φ为颗粒体积分数。

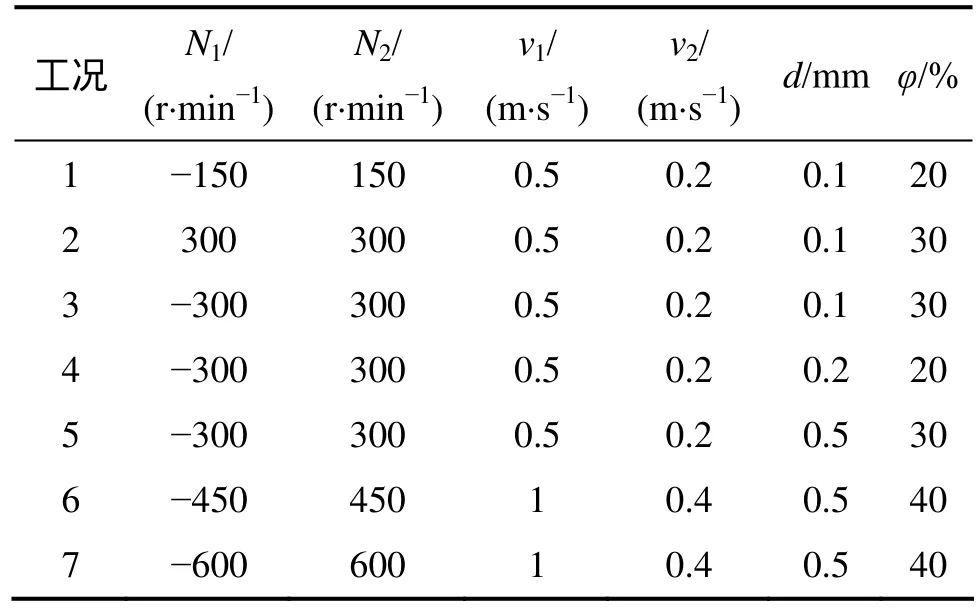
表1 不同的搅拌工况Table 1 Different stirring conditions

3.1 搅拌轴旋向及转速值对速度场的影响

分析在工况1、工况2和工况3时2搅拌轴相对旋转方向和转速对搅拌槽均质混合的影响。

(1) 搅拌轴转速相等时旋转方向对流场的影响。在z=0.495 m截面上速度矢量图如图3所示，当2个搅拌轴的旋向相同(工况2)时流场的平均速度偏大，在搅拌槽内形成1个大循环流，物料间的交叉混合能力差，不利于物料的混合；当2个搅拌轴旋向相反(工况3)时流场的平均速度偏小，在搅拌槽内形成2个旋向相反的循环流场，且漩涡流区域增多，叶片与壁面间产生湍流漩涡有利于混合液的均匀混合，在壁面处的流体也有足够的流速避免流动死角的出现，减少物料堆积。

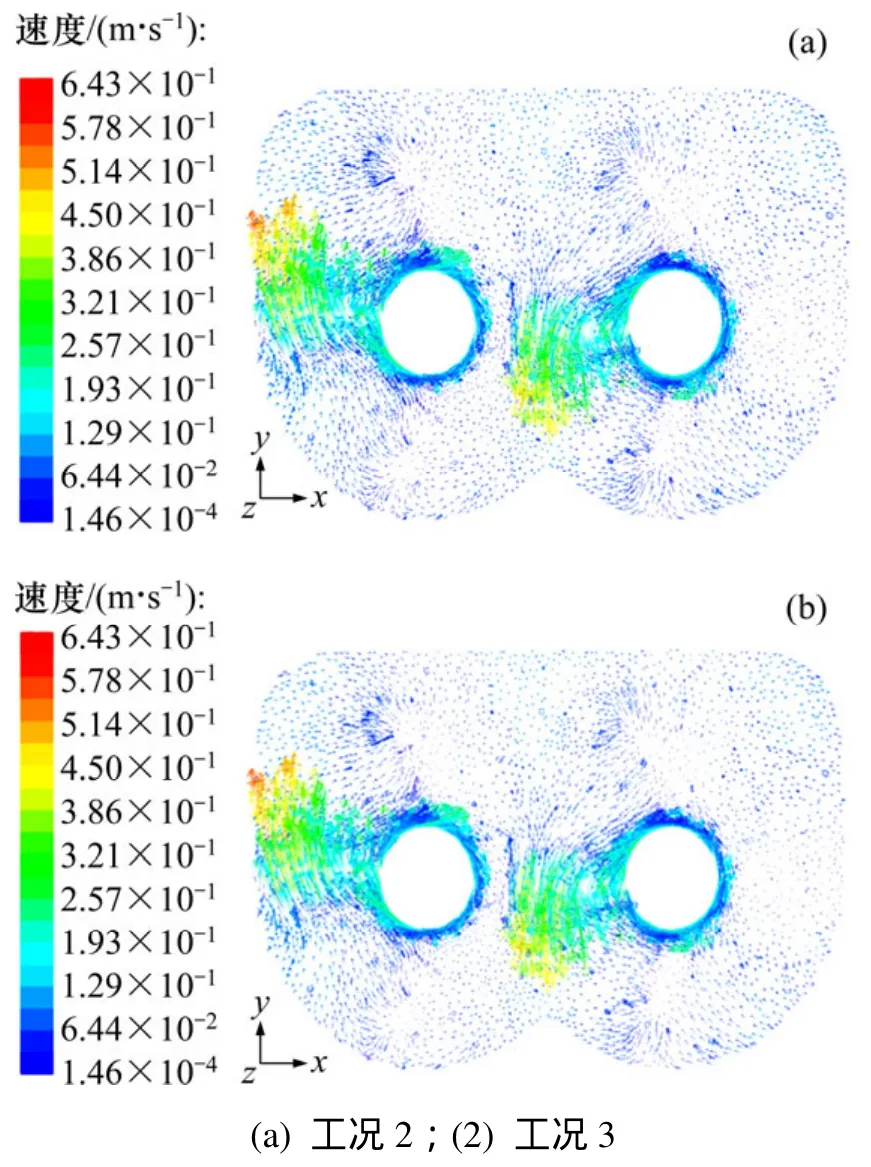
图3 z=0.495 m截面的速度矢量图Fig.3 z=0.495 m section of velocity vector

(2) 搅拌轴的旋向相反时分析转速对流场的影响。在y=0 m的截面上的速度矢量如图4所示。从图4可知：2个搅拌轴旋向相反时叶片之间漩涡湍流作用明显；转速越大流体平均速度越大，流场脉动性越强，越容易形成湍流漩涡，提高颗粒的分散混均效率。

图4 y=0 m截面的速度矢量图Fig.4 y=0 m section of velocity vector

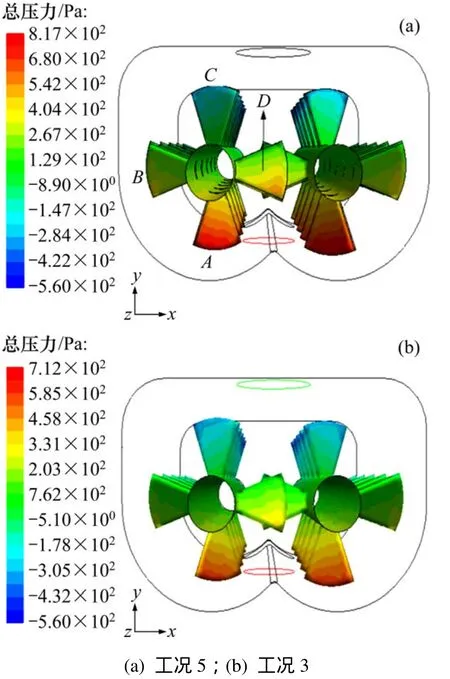
图5 搅拌轴上叶片的总压力云图Fig.5 Total pressure of mixing blades

3.2 不同颗粒直径和不同颗粒质量参数时压力场分析

不同粒径时搅拌轴上叶片的压力如图5所示。由图5可知：颗粒浓度相同时颗粒直径越大，搅拌叶片的平均压力越大。搅拌叶片在不同位置时其压力分布不同，图5(a)中A处的叶片压力梯度大，此处叶片处于搅拌槽底部由于颗粒受到重力、黏滞力、离心力、Gidaspow曳力的作用叶片边缘出现最大压力；B处的叶片受槽壁的影响，其边缘压力偏大；C处的叶片边缘出现负压，上层叶片对流体有抽吸作用利于流场的混合；D处的叶片由于2个搅拌轴在此处交叉混合，叶片上压力梯度明显。

不同粒径时搅拌槽的截面及搅拌槽槽壁的压力分布如图6和图7所示。由图6中截面z=0.135 m的压力分布可知：

(1) 垂直于搅拌轴的截面上总压力呈对称分布，搅拌轴上部出现负压是因为混合液被推动后叶片背面形成空隙造成。

(2) 在不同工况时，由截面z=0.135 m的对称线上固体颗粒的动压力与y方向取值的关系可知：粒径越大，颗粒动压越大，在出口处颗粒的动压力最大，随y方向取值的增大动压力减小，在y=−0.05 m处又开始增大，在搅拌轴附近颗粒动压值瞬间增大且流场湍动能增大，搅拌轴的上方颗粒动压变化很小。由图 7可见：粒径越大，搅拌槽壁面的压力梯度变化越大；不同工况时搅拌槽底部压力随着z增大，总压力增大；粒径越大，压力越大，压力大的地方容易造成槽壁磨损。

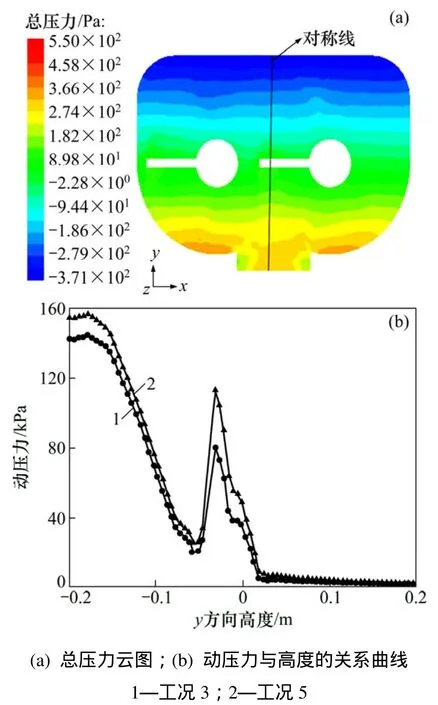
图6 z=0.135 m截面上的总压力云图及动压力与高度的关系曲线Fig.6 z=0.135 m total pressure of mixing blades and relationship between dynamic pressure and height

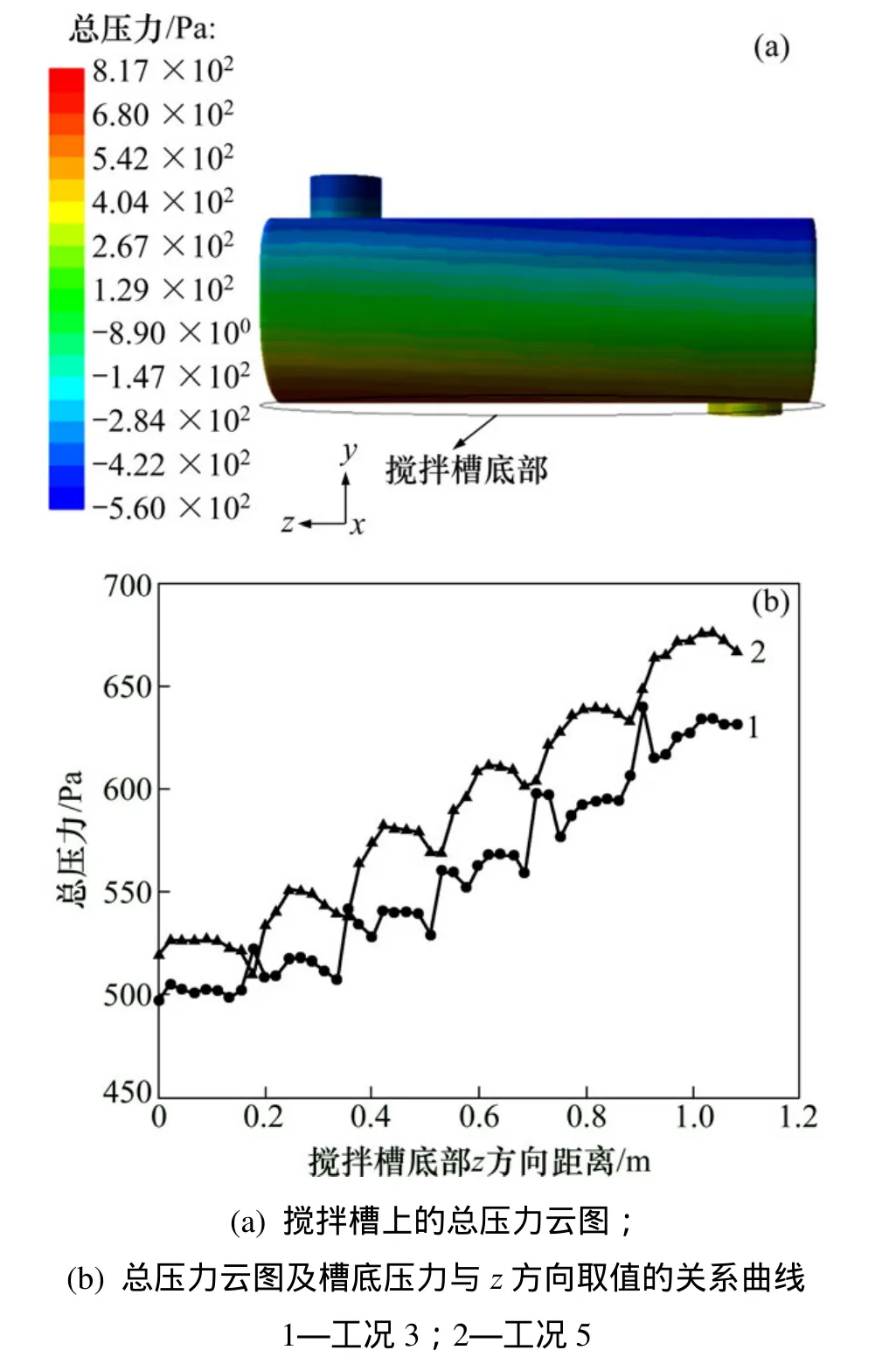
图7 搅拌槽上的总压力云图及槽底压力与z方向取值的关系曲线Fig.7 Total pressure of stirred tank and total pressure changes with z under bottom of Stirred tank

图 8所示为搅拌叶片最大压力随工况的变化情况，其中图 8(a)所示为叶片最大压力与颗粒体积分数的关系。从图 8(a)可见：颗粒体积分数越大，压力越大，在颗粒体积分数小于0.15时压力梯度较大，颗粒体积分数大于0.15大于时压力增大趋势变小；颗粒体积分数大，叶片与颗粒的撞击频率高，颗粒大叶片的撞击力大，叶片易磨损。图8(b)所示为相同体积分数时叶片最大压力与粒径的关系。从图8(b)可见：转速越高颗粒能量大，撞击叶片压力大；粒径增大压力增大；转速小时，叶片最大压力随粒径的变化梯度小，转速变化对叶片最大压力的影响较大。

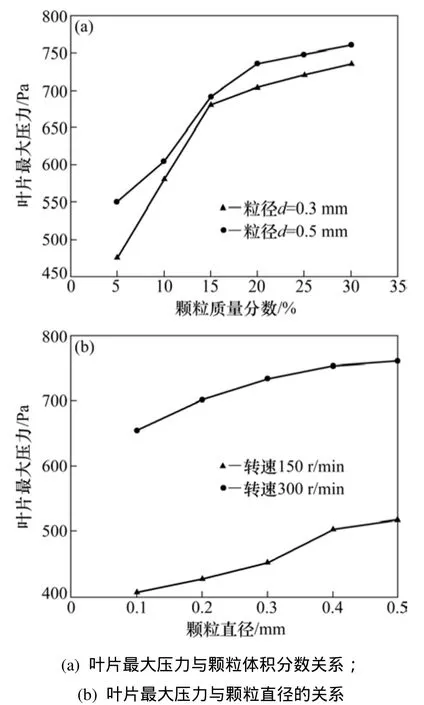
图8 搅拌叶片最大压力随工况的变化Fig.8 Maximum pressure of blades changing with different conditions

3.3 不同叶片螺距时湍流强度及颗粒轨迹线的分析

图9所示为工况3时在z=0.5 m截面上的湍流强度。比较不同螺距的湍流强度可知：螺距小则湍流强度平均值大，湍流强度较大的区域是湍流漩涡出现的区域；湍流强度大，流场的脉动速度大，有利于搅拌混合。

图10所示为不同螺距下颗粒的轨迹线。由图10可见：螺距小叶片数多，叶片与颗粒的碰撞概率大，在径向力和切向力的作用下搅拌均匀性好；螺距大叶片数少，由于重力作用搅拌槽底部颗粒浓度较大，在轴向力作用下快速流向出口，搅拌均匀性差。颗粒在液体中存在抱团的现象，叶片数量多搅拌均匀，混合液受到回流、湍流、二次流作用分散混合性能得到提高。

图9 湍流强度云图Fig.9 Turbulence intensity

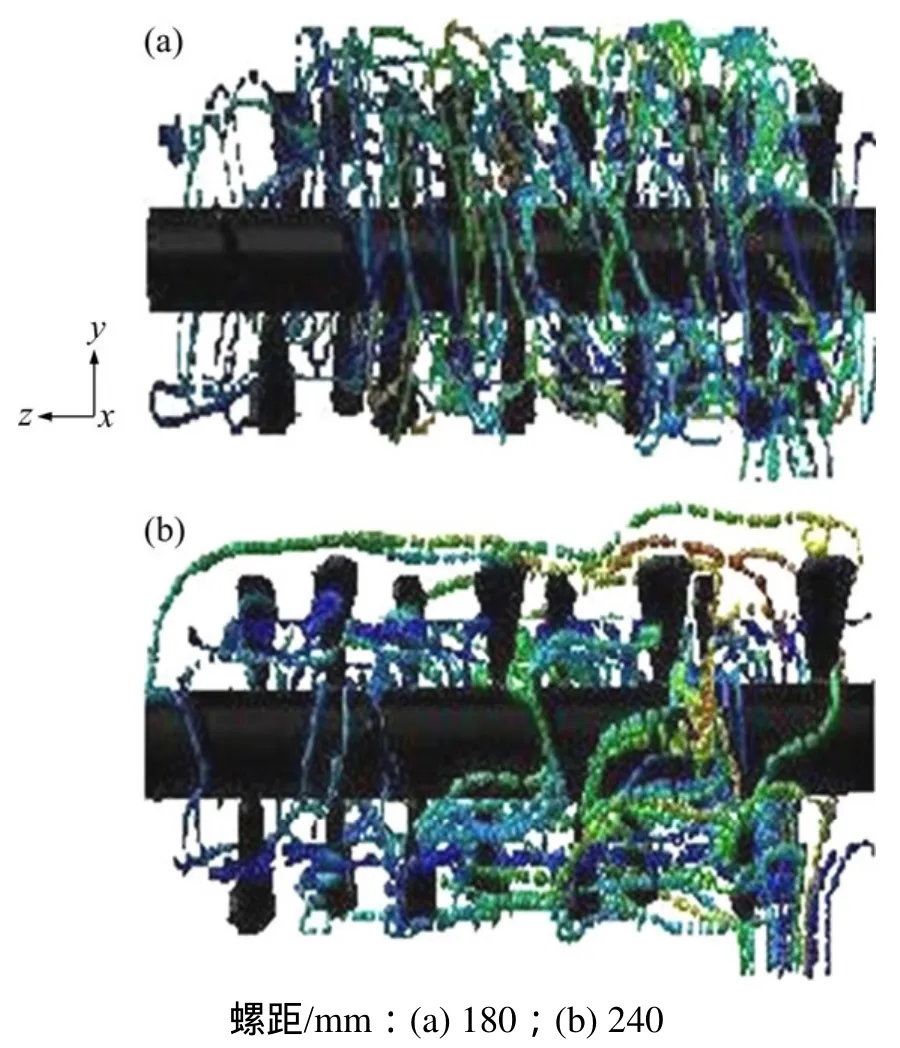
图10 颗粒运动轨迹图Fig.10 Trajectories of particles

3.4 卧式双轴搅拌功率特性分析

在流场特性的分析基础上，选择合理的搅拌参数分析搅拌功率的影响因素。计算不同工况下功率准数NP[13]，求解搅拌槽的理论功率为P1，即为总功率。数值模拟的搅拌功率P由公式P=2πNM计算得到，其中N为搅拌转速，M为数值模拟的搅拌扭矩。数值模拟的搅拌功率即为实际用来搅拌的有用功。定义搅拌效率n=P/P1。分析搅拌轴的功率随粒径、搅拌转速、颗粒体积分数的变化，如图11所示(其中φ为颗粒体积分数，N为搅拌转速)。从下图11(a)～(c)可见：粒径和转速相同时体积分数越大功率越大；粒径和体积分数相同时转速越大功率越大；转速和体积分数一定时随着粒径的增大功率减小，转速越大功率减小的趋势越明显。由图11(d)可见：在双对数坐标系下，当体积分数和粒径不变时，功率随转速近似线性变化。

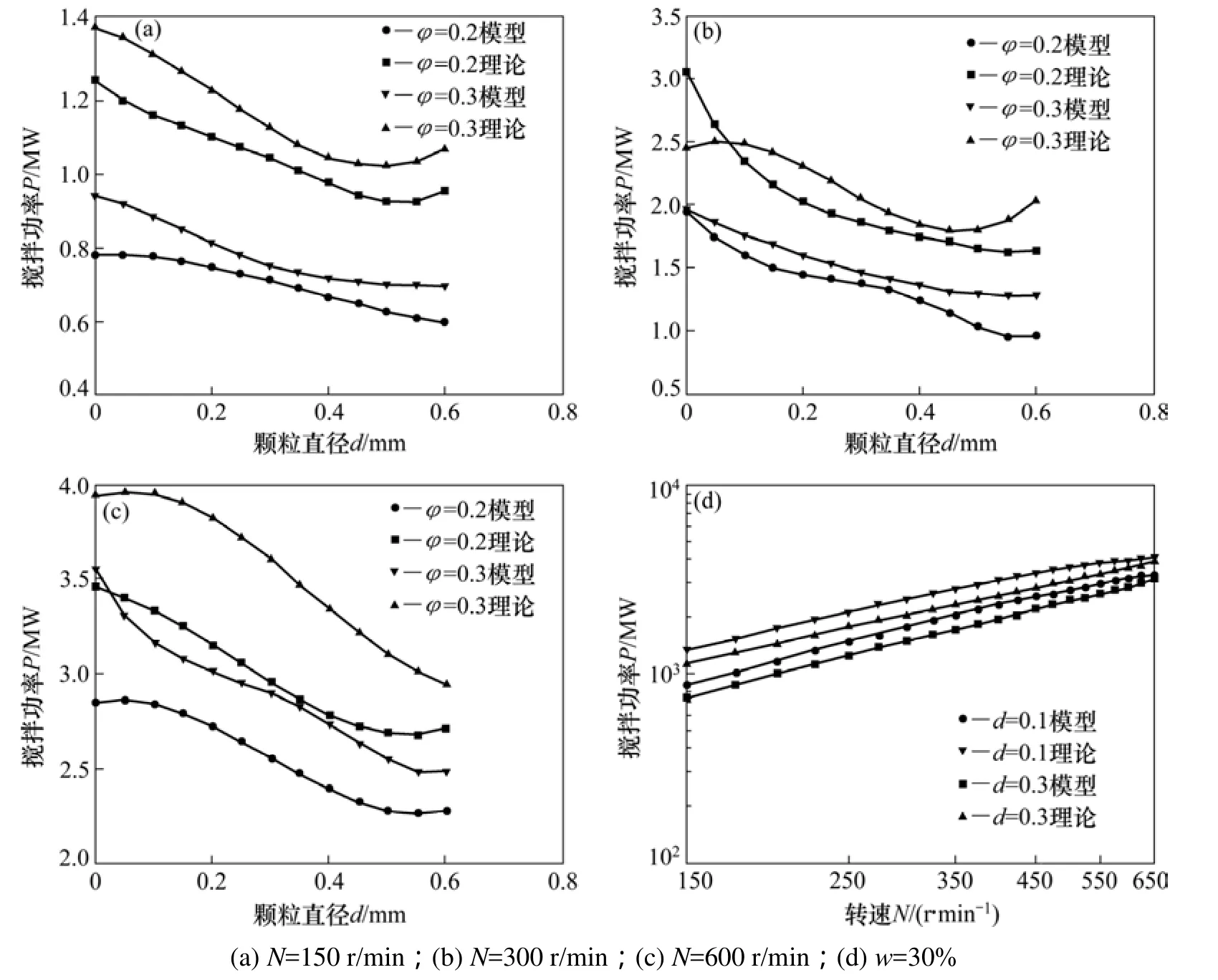
图11 不同工况时搅拌功率的变化情况Fig.11 Mixing power changing with different conditions

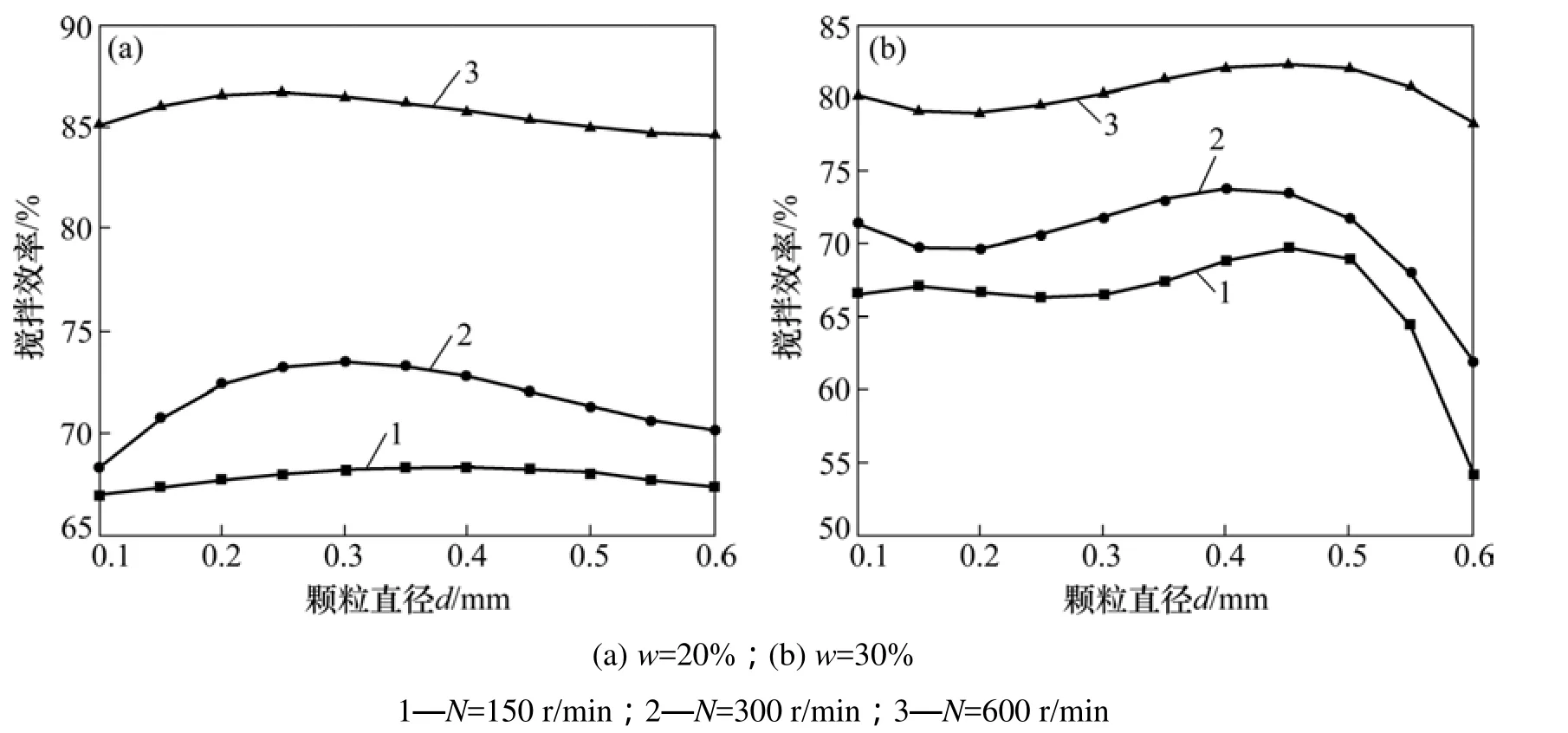
图12 不同工况时搅拌效率的变化关系Fig.12 Mixing efficiency changing with different conditions

分析图12搅拌轴的效率n随着粒径的变化可知：搅拌轴转速高时，搅拌效率高，且搅拌效率对粒径及颗粒体积分数不敏感；搅拌轴转速小时，在体积分数为20%时，随着粒径的增大，效率先升高后降低；粒径为0.3 mm效率最高；当颗粒体积分数为0.3%时，搅拌效率先降低后升高再降低的趋势，最大值约在d=0.5 mm处，随后在低转速时，粒径再增大，搅拌效率快速下降。

3.5 搅拌叶片的磨损率分析

从液固两相流冲刷磨损机理出发，数值模拟分析叶片的磨损率[14−15]。转速相同、颗粒体积分数不同时磨损率随着粒径的变化如图13(a)所示；颗粒体积分数相同而转速不同时磨损率随着粒径的变化如图 13(b)所示。由图13可见：颗粒体积分数大，转速高叶片的磨损严重，在粒径小于0.5 mm时粒径增大，磨损率迅速增加，粒径大于0.5 mm后磨损率变化平缓且出现波动；颗粒体积分数相同时，转速越大磨损量越大，粒径越大，磨损率越大。在双对数坐标系下，粒径 d＜0.5 mm时在磨损率与转速近似成正比。

图13 不同工况时叶片磨损率的变化关系Fig.13 Erosion-wear rate of blades changing with different conditions

4 结论

(1) 螺距小搅拌叶片多，当搅拌转速大颗粒大时，叶片与颗粒的碰撞频率高，颗粒具有的能量大，流场的湍流强度大，有利于液固两相流快速混合。两搅拌轴转向相反，流场脉动速度大，叶片与壁面形成漩涡，壁面处的流体有足够大流速，可避免搅拌死角出现。

(2) 当体积分数和转速不变时，随着颗粒粒径的增大，功率逐渐减小，粒径d＞0.5 mm功率减小的趋势变缓。双对数坐标系下，当体积分数和粒径不变时功率随转速近似线性变化。

(3) 转速大搅拌效率高，转速高时搅拌效率对粒径及颗粒体积分数不敏感。颗粒体积分数小时，搅拌效率变化平稳；体积分数高时，在d＜0.5mm时搅拌效率变化不大，当粒径继续增大时，搅拌效率迅速下降。

(4) 当颗粒体积分数和转速不变时，粒径增大磨损率先增大后趋于平稳；粒径d＞0.5 mm时，磨损率在最大值附近上下波动，颗粒体积分数越大，磨损量越大；当颗粒体积分数一定时，粒径越大则磨损率越大，转速越大则磨损率越大。粒径d＜0.5 mm时双对数坐标系下磨损率与转速近似成正比关系。

[1]Micale G.CFD simulation of particle distribution in stirred vessels[J].Trans IchemE, 2000, 78(A): 435−444.

[2]Montante G, Magelli F.Modelling of solids distribution in stirred tanks: Analysis of simulation strategies and comparison with experimental data[J].International Journal of Computational Fluid Dynamics, 2005, 19(3): 253−262.

[3]Jaworski Z, Bujalski W, Otomo N, et al.CFD study of homogenization with dual rushton turbines-compatarison with experimental results[J].Trans IchemE, 2000, 78(A): 327−333.

[4]Kasat G R, Khopkar A R, Ranade V V.CFD simulation of liquid-phase mixing in solid-liquid stirred reactor[J].Chemical Engineering Science, 2008, 63(15): 3877−3885.

[5]Taghavi M, Zadghaffari R, Moghaddas J, et al.Experimental and CFD investigation of power consumption in a dual Rushton turbine stirred tank [J].Chemical Engineering Research &Design, 2011, 89(3): 280−290.

[6]Dohi N, Takahashi T, Minekawa K, et a1.Power consumption and solid suspension performance of large-scale impellers in gas-liquid-solid three-phase stirred tank reactors[J].Chemical Engineering Journal, 2004, 97(2/3): 103−114.

[7]侯拴弟, 张政, 王英琛, 等.轴流桨搅拌槽三维流场数值模拟[J].化工学报, 2000, 51(1): 70−75.HOU Shuandi, ZHANG Zheng, WANG Yingchen, et al.Numerical simulation of turbulent flow in stirred tank agitated by axial impeller[J].Journal of Chemical Industry and Engineering, 2000, 51(1): 70−75.

[8]钟丽, 黄雄斌, 贾志刚.固−液搅拌槽内颗粒离底悬浮临界转速的CFD模拟[J].北京化工大学学报, 2003, 30(6): 18−22.ZHONG Li, HUANG Xiongbin, JIA Zhigang.CFD modeling of solids just-suspended impeller speed in stirred tanks[J].Journal of Beijing University of Chemical Technology, 2003, 30(6):18−22.

[9]王乐勤, 杜红霞, 吴大转, 等.多层桨式搅拌罐内混合过程的数值模拟[J].工程热物理学报, 2007, 28(3): 418−420.WANG Leqin, DU Hongxia, WU Da-zhuan, et a1.Numerical simulation of mixing process in stirred tank with multiple impellers[J].Journal of Engineering Thermophysics, 2007, 28(3):418−420.

[10]王福军.计算流体力学分析[M].北京: 清华大学出版社,2004: 74−83.WANG Fujun.Computational fluid dynamics analysis[M].Beijing: Tsinghua University Press, 2004: 74−83.

[11]Fluent Inc, GAMBIT Modeling Guide[M].Lebanon: Fluent Inc,2006: 41−88.

[12]Fluent Inc, FULENT User Defined Function Manual[M].Lebanon: Fluent Inc, 2009: 14−24.

[13]王凯, 虞军.搅拌设备[M].北京: 化工工业出版社, 2003:65−70.WANG Kai, YU Jun.Mixing equipment[M].Beijing: Chemical Industry Press, 2003: 65−70.

[14]Fort I, Jirout T.The relation between the rate of erosion wear of a pitched blade impeller and its process characteristics[J].Chemical Engineering Research and Design, 2011, 89(10):1929−1937.

[15]Gnanavelu A, Kapur N, Neville A, et al.An integrated methodology for predicting material wears rates due to erosion[J].Wear, 2009, 267(11): 1935−1944.