一种高压输电塔在风场中的失稳与加固

钟万里，吴灌伦，王伟，吴怡，陈航航

(1.广东电网公司电力科学研究院，广东 广州，510080)2.武汉大学 动力与机械学院，湖北 武汉，430072)

输电线路常见的由机械结构引起的事故有倒杆、倒塔、导线舞动、断线(股)等，造成供电中断，严重威胁电力系统安全稳定运行。输电塔的破坏形式主要有强度破坏和失稳破坏2种，其中在覆冰、强风作用下出现失稳时，将造成倒塔、断线等电网灾害[1]。针对输电塔的动力学建模与分析，Irvine[2]建立了连续体模型，在考虑和忽略缆索刚度2种工况下进行了索塔结构动力学分析；Ozono等[3]在高频段将输电塔简化成悬臂杆，在低频段采用多质点模型，其分析结果与输电塔−线体系平面内动力响应特性基本一致；Yasui等[4]采用梁、桁架单元建立的输电塔−线体系模型，分析其时域响应特性。输电塔的稳定性问题包括风致动力和静力稳定2类。动力稳定是一个引入了时间参数的动态问题，输电塔−线体系的动力特征复杂，关于动态稳定性的判定准如Budiansky−Roth准则、位移相等准则和动态增量法(IDA)等[5]则是研究热点。与风致动力稳定分析相比，输电塔的静力稳定分析避免了动力问题对输电塔带来的风载荷的脉动处理及动力载荷带来的响应上的复杂性，重点对杆塔结构本身的失稳特性进行分析。在此，本文作者以沿海地区多台风的气候为背景，研究典型塔型的失稳模态及其局部加固方法。首先将输电塔的风速载荷转换为风压载荷，在转换过程中，结合技术资料，通过工况系数修正基本风压载荷，以符合输电塔的实际风载荷条件，并具体划分横担风压载荷和塔身风压载荷；其次，参考沿海地区的输电线路设计风速，以30 m/s为基本风速，利用ANSYS软件对输电塔不同加固方案进行非线性屈曲分析。

1 输电塔所受风荷载的计算

1.1 风速与风压的关系

为了确定输电塔所受外载，根据流体力学中的伯努利方程，将风速换算成风压w[6]：

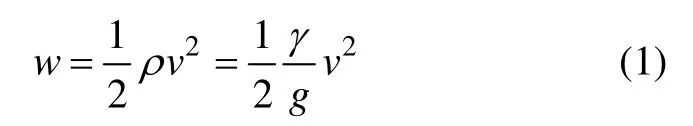
式中：ρ为空气质点密度(t/m3)；γ为空气重力密度(kN/m3)；v为来流风速(m/s)。

基本风压w0不是结构上的风荷载。由于结构的高度及体型结构不同，再考虑脉动风的作用，本文采用高度变化系数μz、体型系数μs和风振系数βz来描述，顺风向总的风载荷为：

式中：基本风压w0中包含着非标准条件的修正。高耸结构设计规范(GB 50135—2006)为重现期不同的情况引入修正系数μr，称为重现期调整系数。对一般高耸结构由于重现期取50 a，μr=1.1；对重要的高耸结构，重现期取 100 a，μr=1.2[6]。

1.1.1 风压高度变化系数μz

不同地貌、不同高度的风压高度变化系数 μz见表1。

1.1.2 风压体型系数μs

风压体型系数 μs为风作用于结构上的实际压力w实际与来流风压w计算之比，即

对工程实际中整个面上特定测点的实际值进行加权平均，可得平均风压体型系数：

其中：A为测点处塔架轮廓面积。根据 SDGJ 94—90(《架空送电线路杆塔结构设计技术规定》)，塔身杆件体形系数取 μs=μst(1+η)μst=0.7，由挡风系数φ和宽厚比B/H确定。

1.1.3 风振系数βz

令T1为系统第1周期，当T1＜0.25 s时，风振系数βz取1；当T1≥0.25 s时，风振影响会随着周期的增大而增大，此时，需考虑脉动风的影响。

表1 风压高度变化系数μzTable 1 Wind pressure – height variation coefficien t μz

1.2 横担与塔身的风荷载计算

根据SDGJ 94—90(《架空送电线路杆塔结构设计技术规范》)，风向垂直于横担到正面时，

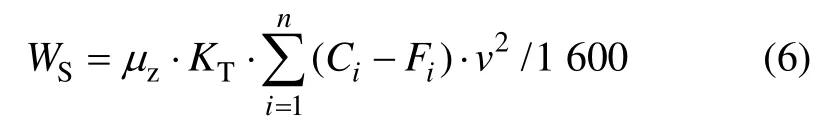
式中：WS为垂直于横担正面总风荷载(kN)；μz为风压随高度的增加系数，按横担形心处距地面高度计算，取B类地貌，则Ci为杆件体型系数(当角钢与槽钢等截面时，取1.4(1+η)；当圆钢与钢管等截面时，设d为圆截面杆件直径(n)；w为计算风压，w=v2/1 000，当 wd2≤0.002时，取 1.2(1+η)；当0.002＜wd2＜0.015时，按线性插入)；风振系数KT和背风面构件体型系数降低系数η分别按表2和表3选用。表2和表3中：Fk与F分别表示横担正面轮廓面积和构件在风力方向投影面积的总和；h为横担高度；b为横担宽度；Fi为横担(塔架)正面某一根构件在风力方向的投影面积(m2)；n为1个面上构件总数；v为计算标高处的高空风速(m/s)。

对塔身，将整塔每隔10～20 m为1段，按式(6)计算风荷载，作用点偏安全地取自下而上的2/3段高处，并忽略组合构件背风面杆件挡风的影响。

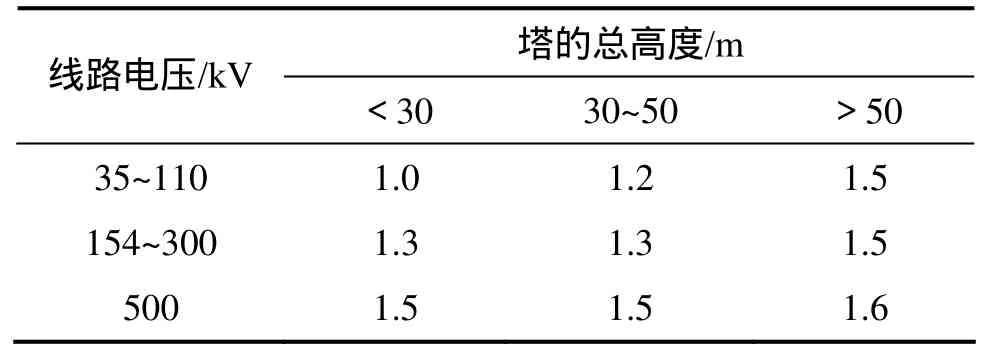
表2 横担(塔)风振系数KTTable 2 Coefficient of wind−induced vibration KT

表3 体型系数降低系数ηTable 3 Shaper reducing coefficient η

2 输电塔抗风稳定性分析

结构失稳(屈曲)问题一般分为2类：第1类是理想化情况，即达到某种荷载时，除结构原来的平衡状态存在外，可能出现第2个平衡状态，又称为分岔失稳或分支点失稳，或称特征值屈曲，此类结构失稳时相应的荷载成为屈曲荷载；第2类是结构失稳时，变形迅速增大，而不会出现新的变形形式，即平衡状态不发生质变，也称极值点失稳[7]。结构失稳时相应的荷载成为极限荷载。此外，还有1种跳跃失稳，当荷载达到某值时，结构平衡状态发生明显跳跃，过渡到非邻近的另一个具有较大位移的平衡状态。由于在跳跃时结构已经破坏，其后的状态不能被利用，所以，归入第2类失稳[8]。

对应于上述2种失稳问题，在利用有限元分析软件ANSYS对输电塔进行稳定性分析时，ANSYS提供了2种分析方法。

(1) 特征值法。该方法用于预测理想弹性结构的理论屈曲强度，是经典的欧拉屈曲分析方法。但是，在实际情况中，由于结构的缺陷和非线性特征很难得到特征值，采用特征值方法往往高估了现实结构的屈曲强度[9]。特征值屈曲分析可以预测出屈曲荷载的上限，为进一步非线性屈曲分析提供了初始加载值。

(2) 非线性法。该方法考虑大变形、非线性等特性进行分析。其分析过程是：逐渐增加荷载，直到达到某个临界值为止，此时结构变得不稳定，即给1个很小的荷载增量，就达到较大变形，这个临界值就是临界荷载。

2.1 第1类稳定问题的屈曲分析及屈曲因子

输电塔在强风下的失效形式主要为杆件受压失稳屈曲[10]。输电塔是由许多单元组成的一个整体，当 1个单元发生失稳形变后，影响相邻的单元，进而引起整个结构的内力重新分布：因此，有必要从整体结构上分析塔的稳定性，即进行屈曲分析[11]。如结构第 1类稳定问题在数学可归结为广义特征值问题，通过对特征值方程的求解，确定结构屈曲时的极限荷载和破坏形态。屈曲特征方程为：

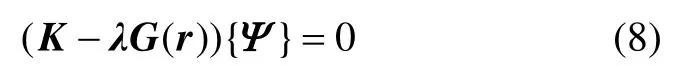
式中：K为刚度矩阵；G(r)为荷载向量 r作用下的几何刚度；λ为特征值对角矩阵；Ψ为特征向量。

通过特征方程求解特征值和相应的特征向量，确定屈曲荷载及其对应的变形形态。每一组“特征值−特征向量”称为结构的1个屈曲模式。特征值λ称为屈曲因子，在给定模式中，它必须乘以r中的荷载才能引起屈曲，即屈曲荷载为屈曲因子与给定荷载的乘积[12]。在一般情况下，可将λ视为安全系数：若λ＞1，则给定的荷载必须增大以引起屈曲；若λ＜1，则需降低外荷才能避免屈曲[13]。

2.2 铁塔屈曲分析

根据沿海地区的线路设计规范，取基本风速为30 m/s的平均风，在此条件下对输电塔进行屈曲分析。首先，在ANSYS中建立输电塔的有限元模型，将所确定的等效风压加载在各层塔迎风面的型材作为分布面载，进行静力分析，分析时，激活预应力影响；定义分析类型、分析选项、荷载步，获得特征屈曲解；扩展静力解。

参考相关研究中的输电塔失稳局部加固策略(见图1)，本文确定2种加固方案。对比现有杆塔无加固的情况，对以下3种工况进行分析。

(1) 工况1：无加固工况。对输电塔进行特征值屈曲计算，提取其前2阶屈曲模态，得到的结果如图2(a)和图 2(b)所示。由塔弹性屈曲模态及其系数见表 4。由表4可知：现有输电塔的一阶和二阶屈曲系数分别为6.121和6.213，满足基本风速30 m/s的设计要求。

当风载继续增加时，可能的失稳部位在塔身主材上。如图2(a)和图2(b)所示，失稳环节在第1和第2段塔身主材上，也就是说，塔身主材为杆塔薄弱环节，为提高输电塔的风载承受力，本文提出主材局部加固补强的方法。

(2) 工况2：塔身第1和第2段主材局部加固，主材面积增加50%。图1(a)所示为对局部加固的示意图。

(3)工况3：塔身第1、第2和第3段主材局部加固，如图1(b)所示。

图1 塔身主材局部加固Fig.1 Partial reinforcements of main part of tower

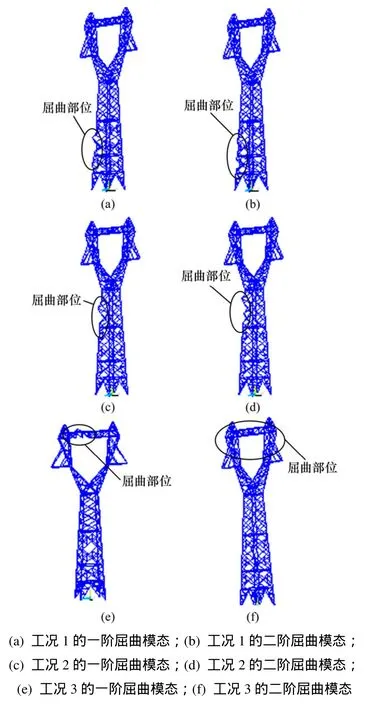
图2 3种工况下的一阶和二阶屈曲模态Fig.2 First and second buckling mode of transmission tower

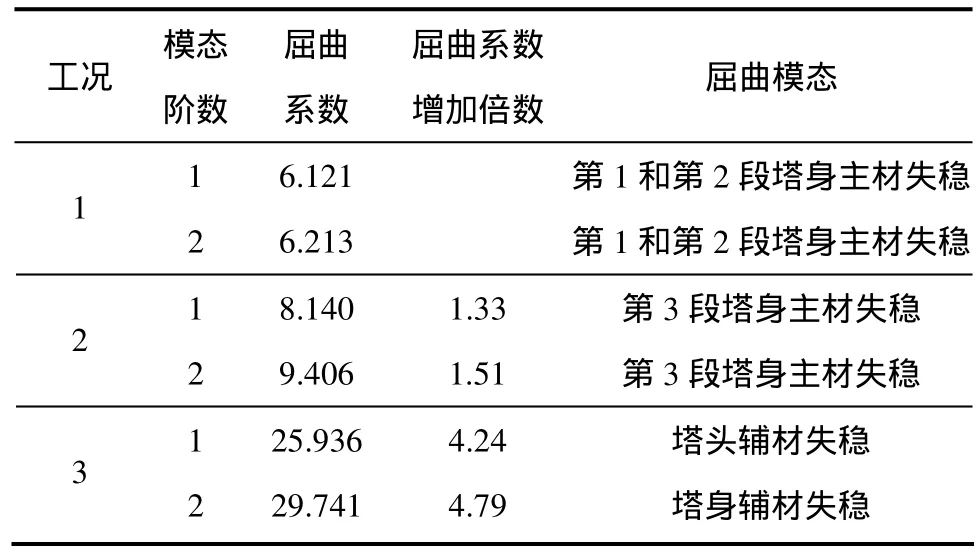
表4 电塔弹性屈曲模态及其系数Table 4 Coefficient and buckling mode of flexibility of electrical towers

为了分析加固对杆塔抵抗屈曲失稳能力的影响，均取基本风速30 m/s，分析结果见表4和图3。从表4和图3可见：加固后输电塔的一阶和二阶屈曲系数分别增大到原来的1.33，1.51，4.24和 4.78；失稳部位从下往上移至横担部位。

3 结果分析

(1) 据现有塔的结构设计，最先发生屈曲失稳的部位是下部第1和第2段塔身；当对下部塔身主材加固后，屈曲失稳的薄弱环节则沿主材往塔顶移。

(2) 对比工况2和工况3这2种加固方案，发现随着主材加固段数的增加，屈曲系数的增加比例增大，加固效果更明显。

(3) 当塔身主材加固后，其失稳部位从主材整体失稳移至辅材的局部屈服，极大地减小了输电塔因主材遭到破坏而发生失稳倒塔的可能性。

(4) 为了提高经济效果，在塔身到达了一定的屈曲系数后，可适当减少第3段主材的加固程度。另外，在采用增加主材截面积方法的同时，可通过探讨截面形状，使塔身的设计得到进一步优化，以此提高塔的整体稳定性，使设计更合理。

4 结论

(1) 通过对输电塔进行失稳分析，对其发生失稳破坏的薄弱环节进行加固改造，其失稳部位从主材整体失稳移至辅材的局部屈服，从塔身主材移向塔顶，减小了输电塔因主材遭到破坏而发生失稳倒塔的可能性，能够保证输电塔结构在外荷载作用下足够安全。

(2) 对所述类型的输电塔，随着主材加固段的增加，屈曲系数的增加比例增大，加固的效果更明显。为了提高输电塔的抗屈曲失稳能力，应同时加固塔身的3段主材，当抗屈曲系数达到一定要求后，可以适当降低第3段塔身主材的加固程度，以提高经济效果。

(3) 采用局部加固的方法适当加固塔身主材，并合理选择主材截面形状的设计方式可以使输电塔整体稳定性提高。

[1]张勇.输电线路风灾防御的现状与对策[J].华东电力, 2006,34(3): 28−31.ZHANG Yong.Status quo of wind hazard prevention for transmission lines and countermeasures[J].East China Electric Power, 2006, 34(3): 28−31.

[2]Irvine H M.Cable structures[M].Cambridge: MIT Press, 1981:1−20.

[3]Ozono S, Maeda J.In-plane dynamic interaction between a tower and conductors at lower requences[J].Engineer Structure,1992, 14(4): 210−216.

[4]Yasui H, Marukawa H, Momomura Y.Analytical study on wind-induced vibration of power transmission tower[J].Journal of Wind Engineering and Industrial Aerodynamics, 1999, 83(2):431−441.

[5]李庆伟, 李宏男.输电塔结构的动力稳定性研究[J].防震减灾工程学报, 2008, 28(2): 202−207.LI Qingwei, LI Hongnan.Study on dynamic instability of transmission tower[J].Journal of Disaster Prevention and Mitigation Engineering, 2008, 28(2): 202−207.

[6]王肇民.高耸结构设计手册[M].北京: 中国建筑工业出版社,1995: 11−32.WANG Zhaomin.Towering structure design handbook[M].Beijing: China Building Industry Press, 1995: 11−32.

[7]邓长根, 吴建华, 甘东华.钢结构失稳监测方法和失稳监控部件研究[J].建筑科学与工程学报, 2006, 23(3): 21−25.DENG Changgen, WU Jianhua, GAN Donghua.Research on instability monitoring methods and instability monitoring components for steel structures[J].Journal of Architecture and Civil Engineering, 2006, 23(3): 21−25.

[8]陈晓明, 邓洪洲, 王肇民.大跨越输电线路舞动稳定性研究[J].工程力学, 2004, 21(1): 56−60.CHEN Xiaoming, DENG Hongzhou, WANG Zhaomin.Conductor galloping stability analysis of long-span transmission system[J].Engineering Mechanics, 2004, 21(1): 56−60.

[9]张朝晖.ANSYS 8.0结构分析及实例解析[M].北京: 机械工业出版社, 2005: 120−134.ZHANG Zhaohui.Structural analysis and examples of resolution of ANSYS 8.0[M].Beijing: Mechanical Industry Press, 2005:120−134.

[10]江宜城, 钟寅亥, 樊剑, 等.黏弹性阻尼器控制下大跨越输电塔风振响应分析[J].钢结构, 2003, 18(4): 34−36.JIANG Yicheng, ZHONG Yinhai, FAN Jian.Wind vibration responses analyses for electrical transmission tower with viscoelastic dampers under wind load[J].Steel Construction,2003, 18(4): 34−36.

[11]何艳丽, 王增春, 董石麟, 等.桅杆结构的内共振对其动力稳定性的影响[J].钢结构, 2001, 16(3): 38−42.HE Yanli, WANG Zengchun, DONG Shilin, et al.Effect of internal resonance of mast structure on its dynamic stability[J].Steel Construction, 2001, 16(3): 38−42.

[12]邓洪洲, 吴昀, 刘万群, 等.大跨越输电塔结构风振系数研究[J].特种结构, 2006, 23(3): 66−69.DENG Hongzhou, WU Jun, LIU Wanqun, et al.Span transmission tower structure of wind-induced vibration coefficient[J].Special Structures, 2006, 23(3): 66−69.

[13]李雪, 李宏男, 黄连壮.高压输电线路覆冰倒塔非线性屈曲分析[J].振动与冲击, 2009, 28(5): 111−114.LI Xue, LI Hongnan, HUANG Lianzhuang.Nonlinear buckling analysis of collapsed steel tower for 220 kV Guajing iced transmission line[J].Journal of Vibration and Shock, 2009, 28(5):111−114.