纤维混凝土力学性能分析的随机双尺度模型

贺鹏飞，刘 书，柳 献，袁 勇

（1.同济大学 应用力学研究所，上海200092；2.同济大学 土木工程学院，上海200092）

短纤维增强混凝土是一种以混凝土为基体，以金属纤维、无机非金属纤维、合成纤维或天然有机纤维为增强相的复合材料.这些短而细且随机均匀分布的纤维起着阻止基体中原有微裂缝的扩展并延缓新裂缝产生从而改善基体的韧性与抗冲击性的作用［1］.近年来短纤维增强混凝土凭借其强度高、模量大、比重小、耐腐蚀性好以及其他方面的优越性能受到了越来越广泛的关注［2］.

在实际应用中，为了更好地开发、利用短纤维增强混凝土，首先要能够较好地预测其弹性常数，这也是后续强度计算、结构设计的基础.而短纤维增强混凝土的力学性能不但与基体的性能有关，还与细观特征及纤维增强相关，所以从细观层面建立合适的模型来精确地预测其力学性能是十分必要的.

目前纤维增强复合材料力学性能的研究方法以细观力学为主，常见的包括自洽法［3］、广义自洽法［4－5］、Mori－Tanaka方法［6－7］、均匀化理论［8－10］等.20世纪70 年 代 Lions［11］，Kesavan［12－13］在 均 匀 化 理 论的基础上提出了结合有限元的双尺度渐近分析方法，并对复合材料进行有效性能的预报.在过去的10年中，双尺度分析方法取得了很多成果.崔俊芝和曹礼群［14－16］给出了整周期复合材料弹性结构的双尺度渐近展开式并在数学上证明了双尺度渐近解是收敛于真实解的.之后，Yu等［17］将双尺度渐进展开法应用到纤维编织复合材料的力学性能预测上.Li等［18］利用这种方法提出了一种新的统计双尺度模型，并计算分析了随机分布颗粒复合材料的力学性能参数.

随着研究的深入，双尺度方法在周期或拟周期复合材料力学性能计算方面的应用越来越广泛.但是，之前的这些双尺度模型并不能有效地应用到短纤维增强混凝土中，因为其中短纤维乱向随机分布的材料特点不能被很好地刻画.本文通过定义新的随机单胞模型将双尺度方法与短纤维增强混凝土材料结合.

1 随机双尺度模型

1.1 单胞的描述

已有的单胞模型主要是通过生成随机分布的球形颗粒或者椭球颗粒来模拟随机颗粒增强复合材料或者是模拟连续纤维增强复合材料（单向纤维增强复合材料和编织复合材料）.这2种单胞模型均不能很好模拟短纤维增强混凝土，第1种单胞在增强相形状方面不能很好模拟短纤维，第2种单胞不能模拟短纤维增强相随机乱向分布的特性.

正如随机颗粒增强材料一样，短纤维作为增强相也是随机分布的，不同的是本单胞模型的增强相形状不再是圆形或椭球颗粒，而是随机分布的圆柱体，如图1，图中Γu和Γt分别表示位移边界和力边界、参数ε表示单胞尺寸、x表示宏观坐标系、引入细观局部坐标y＝x／ε，所研究材料的物理量受2个参数的控制，x和y，其中x表示宏观尺度的变化，而y主要用来反映局部细观尺度的信息.

单胞尺寸ε相对于材料宏观结构的几何尺度是非常小的量，0≪ε≪1.然而为了较为精确地评估力学性能，对于含有乱向随机分布纤维的短纤维增强混凝土来说，一个简单的单胞是不够的，因此引入随机参数，在单胞中随机生成满足相同概率分布模型的圆柱体来模拟短纤维，其余模拟混凝土基体.每个圆柱体有7个参数，其中位置参数：圆柱体底面中心坐标（yi，1，yi，2，yi，3），其中i表示单胞中第i个圆柱体；尺寸参数：母线长度L、半径R；方向参数：圆柱体母线与y3轴的夹角θ，圆柱体母线在坐标系y1Oy2平面上的投影与y1轴的夹角φ.其中位置参数和方向参数服从均匀分布概率模型，而尺寸参数根据实际纤维尺寸进行模拟，在各自范围内服从均匀分布，这样单胞内所含圆柱体的体积分数可以根据纤维体积分数实际值有效控制.

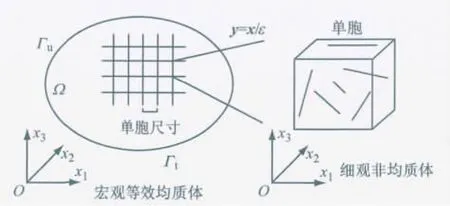
图1 宏观结构与细观特征体Fig.1 Macro－structure and representative element volume（REV）

在一个单胞内，n为生成的圆柱体的数量，因此，可以定义相应的分布模型w.

按上述表征方法，任何短纤维增强混凝土结构都可以看成是由具有相同分布模型的单胞组合而成.

式中：t为单胞个数；Q表示一个单位化单胞，单胞尺寸为1；ε表示单胞尺寸，相应的圆柱体分布模型为w.认为宏观点x是由单胞周期性排列组成，定义

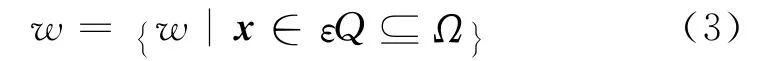
1.2 随机双尺度分析

当宏观结构受到外部荷载的作用时，由于该材料细观层次的高度非均质性，使得结构场变量（如位移、应变和应力等）在宏观位置x的非常小的邻域ε内有很大的变化［11］.双尺度的本质是认为宏观上均质的材料在细观尺度上是非均质的，在单胞内将材料结构力学量表示成关于宏观坐标x和细观坐标y的函数，这样将材料的宏观性能与细观非均质结构联系一起.

由固体弹性力学可知，混合边界条件下弹性问题可以表述为［15］

式中：aijhk（x，w）（i，j，h，k＝1，2…，n）为等效均质体上一点x处对应单胞内材料组分的刚度系数；fi（x）为线弹性体所受体力分量.u（x，w）为位移矢量.所满足的边界条件为

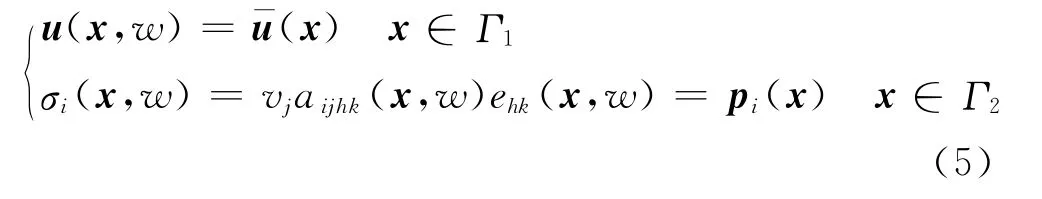
式中：Γ1和Γ2分别表示位移边界和力边界；vj（j＝1，2，…，n）为力边界Γ2的外法线方向余弦；σi（x，w）为单胞边界处应力（x）和pi（x）分别为对应位移边界和力边界上的给定位移和载荷.其中

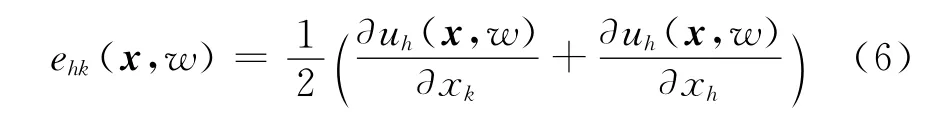
同时考虑到构件宏观参数和细观特征对位移u（x）的影响，在宏观坐标系x（x1，x2，x3）和细观局部坐标系y（y1，y2，y3）下有以下位移展开式［16］：

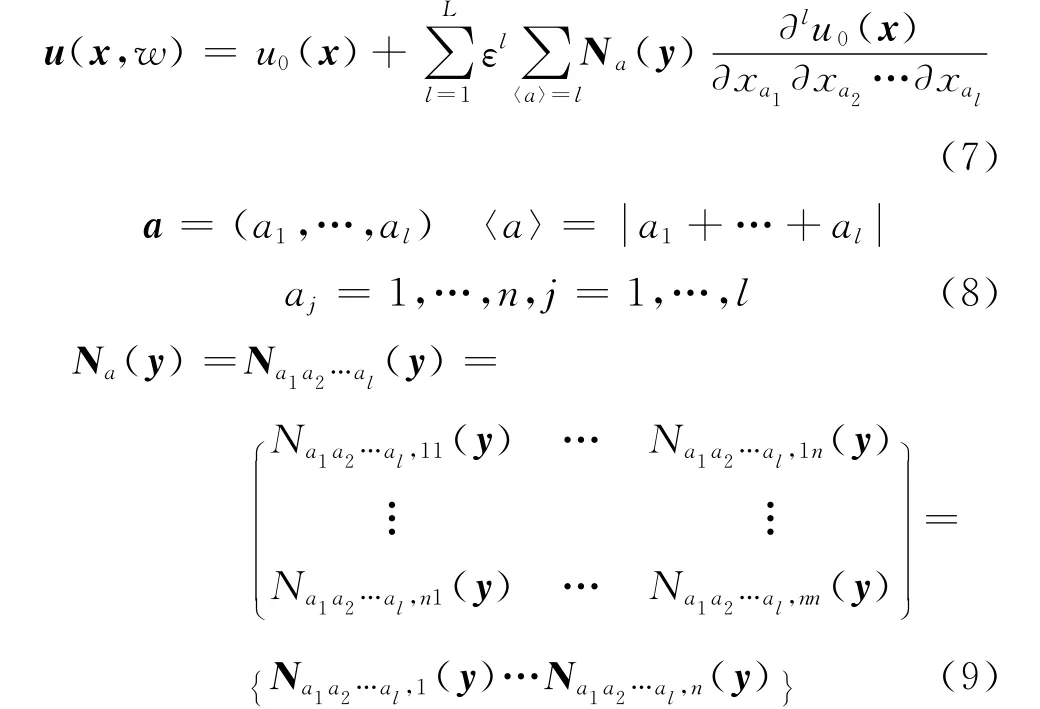
式中：u0（x）为宏观整体结构Ω上的均匀化位移解；L为计算阶数；Na（y）为单胞矩阵向量函数，反映复合材料结构细观特征的影响.

将式（7）代入式（4）中，因为ε→0，所以εn（n＝－2，－1）的系数必须为零，进而可到单胞形函数Na（y）满足的方程［17］，进而求解出均匀化刚度系数（w）.

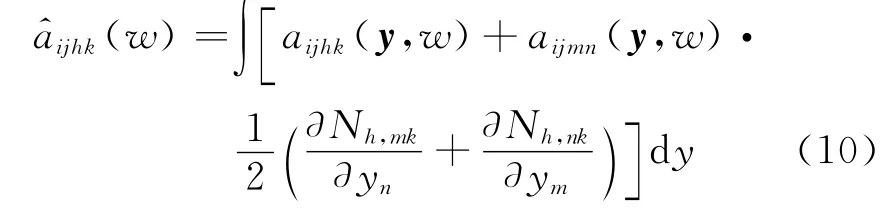
从式（10）可以看出，均匀化刚度系数a＾ijhk（w）不仅和单胞内组分材料的刚度系数aijhk（x，y，w）有关，还决定于反映单胞局部不均匀性的形函数.进而由式（4）和式（10）求得宏观均匀化位移解u0（x）.

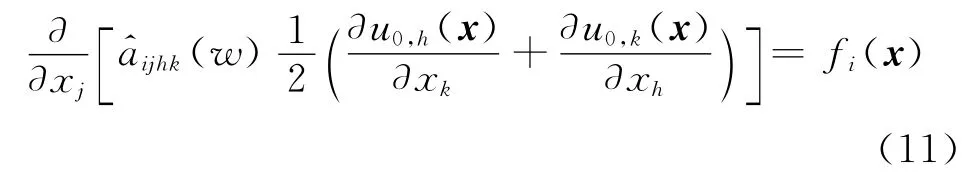
进而得到考虑细观特征影响的位移场分布u（x，w）.根据弹性力学几何和物理方程，求出相应的更为精确的应变场［17］.

2 模型验证

为了对给出的随机双尺度模型的有效性进行验证，在钢纤维增强混凝土试验数据［19］的基础上将本文模型的计算结果与试验结果进行对比，各组分材料的力学参数见表1.

表1 混凝土基体和钢纤维力学性能参数［19］Tab.1 Mechanic parameters of concrete matrix and fiber［19］

在单胞内生成满足随机分布的圆柱体来模拟钢纤维，其余模拟等效均质混凝土基体，其中单胞尺寸为5mm×5mm×5mm，圆柱体直径为300～800 um，母线长为2～5cm，圆柱体直径D和母线长L在各自范围内服从均匀分布，满足一定体积分数，并且相互之间不重合.对分布模型为w的单胞采用10节点四面体单元进行网格划分，如图2，建立单胞有限元模型，利用有限元方法进行求解，得到考虑细观特征影响的均匀化刚度系数a＾ijhk（w），对M个单胞进行重复计算，根据Kolmogorov强大数定理便可得到考虑纤维随机分布精确度更高的解aijhk，H（x）.

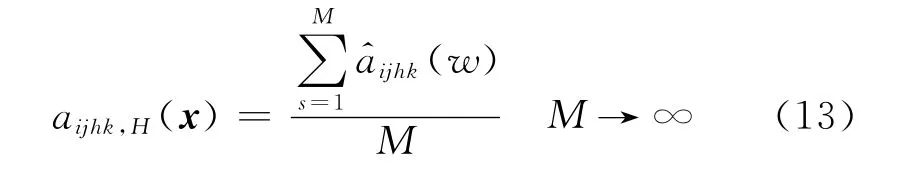
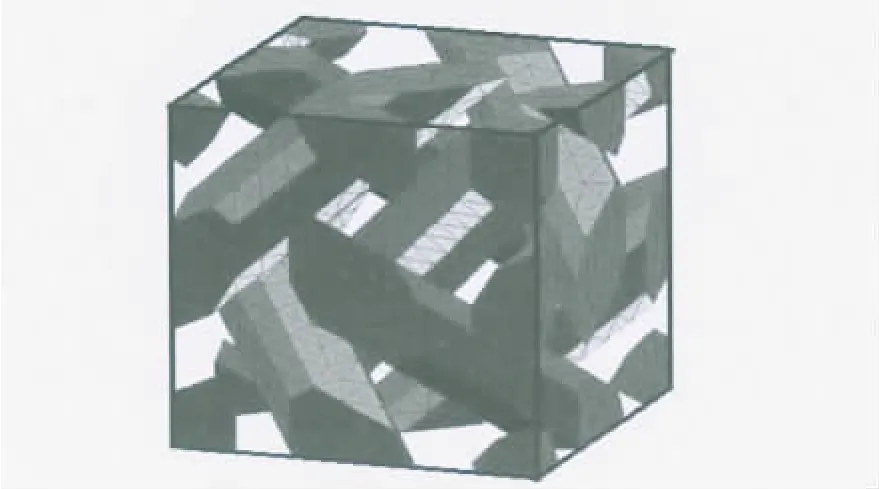
图2 整个单胞有限元模型Fig.2 The entire FEM model of REV

计算对比结果如图3所示，可以发现，本文模型能给出一个很好的预测.为了进一步确定随机双尺度模型在预测短纤维增强混凝土弹性常数方面的有效性，再次利用此模型计算了钢纤维增强混凝土的弹性模量，与试验结果［20］进行对比，各组分材料的力学参数见表2；并选取了其他常用方法［21－22］进行计算分析.

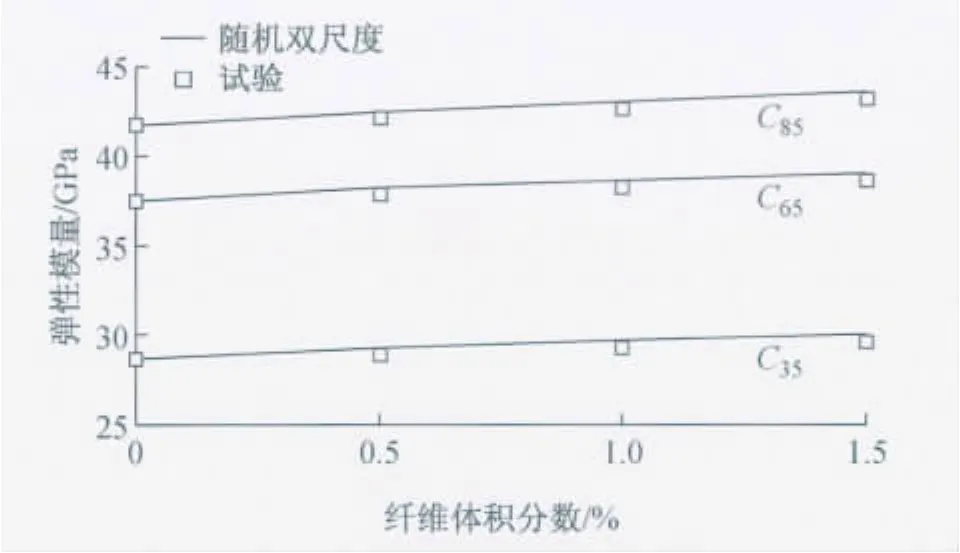
图3 弹性模量计算结果与试验结果对比Fig.3 Comparison of computation and the measured elastic modulus

表2 混凝土基体和钢纤维力学性能［20］Tab.2 Mechanic parameteres of concrete matrix and steel fiber［20］

从图4中与试验结果的对比可以发现，本文模型和其他经典模型都能给出很好的预测，但随机双尺度模型的预测更加接近真实的试验结果，误差在0.8%以内，能够较为精确地预测短纤维增强混凝土的弹性常数.文献［21］方法给出的结果比试验值小，而文献［22］方法给出的结果偏大；并且随着纤维体积分数的增加，这2个模型的误差逐渐增大，而随机双尺度模型的误差则趋于平稳.由此得出结论，本文给出的随机双尺度模型能够更为精确地预测短纤维增强混凝土弹性常数.

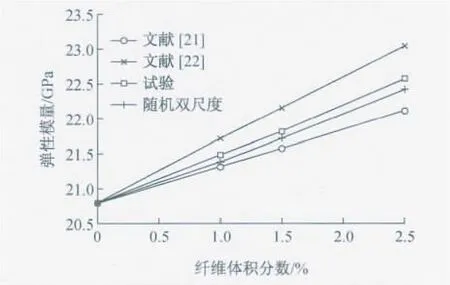
图4 不同模型弹性模量与纤维体积分数关系Fig.4 Elastic modulus with different fiber volume fractions for different models

3 短纤维增强混凝土弹性常数分析

选取工程中常用的钢纤维、PP纤维（聚丙烯纤维）、玻璃纤维和碳纤维（T300）4种纤维模拟高模量纤维混凝土和低模量纤维混凝土，基体混凝土和各纤维的力学性能参数见表3.

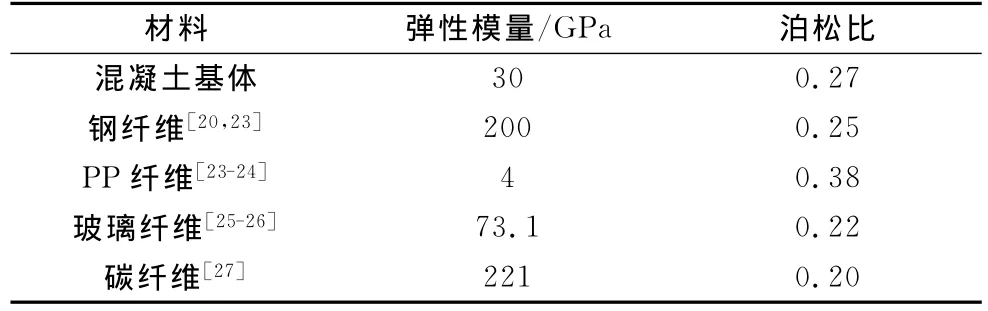
表3 混凝土基体和几种纤维力学性能Tab.3 Mechanic parameters of concrete matrix and different fibers

已有的研究表明，对于现有的乱向短纤维增强混凝土，纤维由于受到重力效应和边壁效应的影响，很难均匀分布.而纤维的体积分数或长径比增大后，在搅拌时容易产生结团现象，目前纤维体积分数仅能达到1%～3%［28］.故结合实际情况对4种纤维不同体积分数下的弹性常数进行对比分析.在单胞内生成满足随机分布的圆柱体来模拟纤维，其余模拟等效均质混凝土基体，其中，单胞尺寸为5mm×5 mm×5mm，圆柱体直径为300～800um，母线长为2～5cm，R和L在各自范围内服从均匀分布，满足一定体积分数，并且相互之间不重合.

图5中Ehom为宏观等效均质体弹性模量，Em为混凝土基体弹性模量.可以看出，由于钢纤维、玻璃纤维、碳纤维的弹性模量大于混凝土基体的弹性模量，在未产生裂纹之前，短纤维增强混凝土的弹性模量随纤维体积分数的增大而增大，与“混合定律”吻合很好；而PP纤维的弹性模量小于混凝土基体的弹性模量，所以随着纤维体积分数的增大反而出现了减小的情况.并且不同纤维种类对弹性模量的影响很明显.由于钢纤维和碳纤维的弹性模量接近，所以2种短纤维混凝土弹性模量提升的效果也相近，都大于玻璃纤维.如在纤维体积分数为1.50%时，钢纤维和碳纤维的提升效果仍分别达到了相近的4.80%和4.70%，大于玻璃纤维的1.48%，相反PP纤维的降低了2.27%.

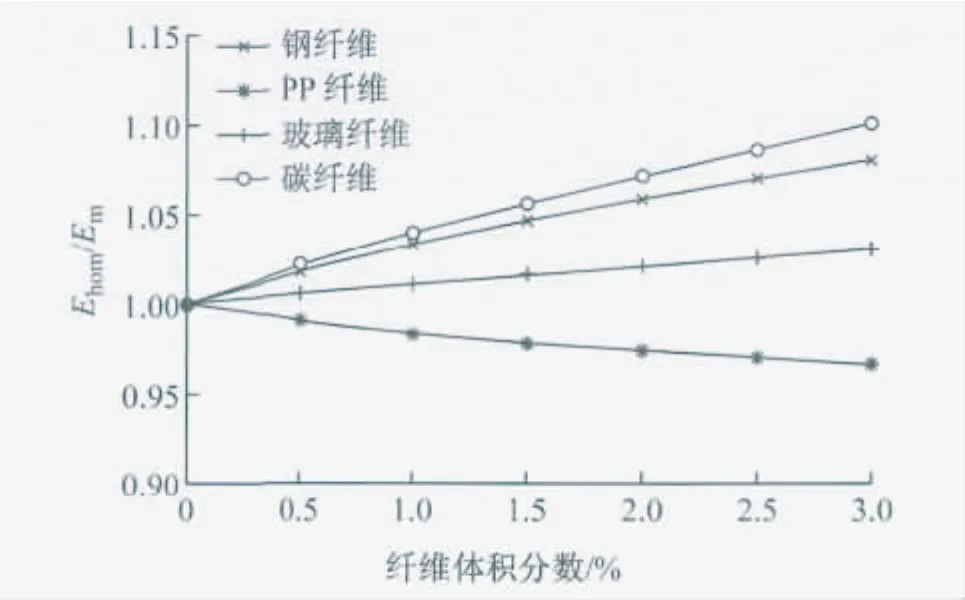
图5 不同纤维Ehom／Em和体积分数的关系Fig.5 The influence of fiber’s type and volume fraction on elastic modulus

图6 中μhom为宏观等效均质体泊松比，μm为混凝土基体泊松比.可以看出，随着体积分数的增加，泊松比的变化和纤维种类的关系与弹性模量相反；但是等效泊松比并没有太大幅度的变化，不同的纤维种类差别不大，并且随着体积分数的增大变化也甚微.主要有两点原因：一是混凝土基体和纤维的泊松比差别不大，二是纤维体积分数很小，所以等效泊松比主要由混凝土基体决定，基本不变.

图6 不同纤维μhom／μm和体积分数的关系Fig.6 The influence of fiber’s type and volume fraction on Poisson’s ratio

通过以上的对比分析可以得出结论，短纤维增强混凝土弹性模量受纤维种类和纤维体积分数影响较为明显.在4种纤维中，钢纤维和碳纤维具有较高的弹性模量，从而相应的纤维增强混凝土模量提升效果比玻璃纤维明显，属于高模量纤维混凝土；而PP纤维的弹性模量较低，会使相应的纤维混凝土的弹性模量和剪切模量降低，属于低模量纤维混凝土.而等效泊松比主要由基体混凝土决定，所以受纤维种类和纤维体积分数影响有限.

4 结语

以双尺度方法为理论基础，将短纤维混凝土的细观结构与宏观力学性能相结合，通过引入服从均匀随机分布模型的随机参数定义了新的单胞模型，单胞中按照一定纤维体积分数随机生成的圆柱体很好地模拟了短纤维混凝土中乱向均匀分布的短纤维，并且给出了该模型结合有限元方法的计算方法.

接着利用提出的随机双尺度模型计算了钢纤维混凝土的弹性模量，并与试验结果及其他经典方法进行对比，验证了此模型在分析短纤维增强混凝土弹性性能方面的有效性.

进而选取了目前工程中常用的4种纤维即钢纤维、PP纤维、玻璃纤维、碳纤维研究分析了短纤维增强混凝土的弹性常数与纤维种类和体积分数的关系.短纤维增强混凝土弹性模量受纤维种类和纤维体积分数影响较为明显，而等效泊松比主要是由基体混凝土决定，所以受纤维种类和纤维体积分数影响有限.

［1］Hannant D J.Fiber cements and fiber concretes［M］.New York：Wiley，1978.

［2］孙成访，谷倩，彭少民.喷射纤维混凝土的性能与应用综述［J］.混凝土，2008，8（8）：101.SUN Chengfang， GU Qian， PENG Shaomin.General introduction of the performance and application of sprayed FRPC［J］.Concrete，2008，8（8）：101.

［3］Gonzalez C，Lorca J L.A self－consistent approach to the elastoplastic behavior of two－phase materials including damage ［J］.Journal of the Mechanics and Physics of Solids，2000，48（4）：675.

［4］DONG X N，ZHANG X H.A generalized self－consistent estimate for the effective elastic moduli of fiber－reinforced composite materials with multiple transversely isotropic inclusions ［J］.International Journal of Mechanical Sciences，2005，47（6）：922.

［5］JIANG C P，TONG Z H.A generalized self－consistent method for piezoelectric fiber reinforced composites under anti－plane shear［J］.Mechanics of Materials，2001，33（4）：295.

［6］Benveniste Y.A new approach to the application of Mori－Tanaka’s theory in composite materials ［J］.Mechanics of Materials，1987，6（2）：147.

［7］Koyama S，Katano S.A modification of the Mori－Tanaka estimate of average elasto－plastic behavior of composites and polycrystals with interfacial debonding ［J］.Mechanics of Materials，2011，43（10）：538.

［8］Guedes J M，Kikuchi N.Pre－processing and post－processing for materials based on the homogenization method with adaptive finite element method ［J］.Computer Methods in Applied Mechanics and Engineering，1990，83（3）：143.

［9］Gal E，Ganz A，Chadad L，et al.Development of a concrete unit cell［J］.International Journal for Multiscale Computational Engineering，2008，6（5）：499.

［10］Gal E，Kryvoruk R.Meso－scale analysis of FRC using a two－step homogenization approach［J］.Composite Structure，2011，89（11）：921.

［11］Lions J L.Some methods in the mathematical analysis of systems and their control.Beijing：Science Press，1981.

［12］Kesavan S.Homogenization of elliptic eigenvalue problemsⅠ［J］.Applied Mathematics and Optimization，1979，5（1）：153.

［13］Kesavan S.Homogenization of elliptic eigenvalue problemsⅡ［J］.Applied Mathematics and Optimization，1979，5（1）：197.

［14］崔俊芝，曹礼群.基于双尺度渐近分析的有限元算法［J］.计算数学，1998，20（1）：89.CUI Junzhi，CAO Liqun.Finite element method based on twoscale asymptotic analysis［J］.MathematicaNumericaSinica，1998，20（1）：89.

［15］曹礼群，崔俊芝.整周期复合材料弹性结构的有限元计算［J］.计算数学，1998，20（3）：279.CAO Liqun，CUI Junzhi.Finite element computation for elastic structures of composite material formed by entirely basic configurations［J］.MathematicaNumericaSinica，1998，20（3）：279.

［16］曹礼群，崔俊芝.整周期复合材料弹性结构的双尺度渐近分析［J］.应用数学学报，1999，22（1）：38.CAO Liqun，CUI Junzhi.The two－scale asymptotic analysis for elastic structures of composite materials with only including entirely basic configuration ［J］.ActaMathematicaApplicatae Sinica，1999，22（1）：38.

［17］Yu X G，Cui J Z.The prediction on mechanical properties of 4－step braided composites via two－scale method ［J］.Composite Science and Technology，2007，67（3／4）：471.

［18］Li Y Y，Cui J Z.The multi－scale computational method for the mechanics parameters of the materials with random distribution of multi－scale grains［J］.Composite Science and Technology，2005，65（9）：1447.

［19］Thomas J，Ramaswamy A.Mechanical properties of steel fiberreinforced concrete ［J］.Journal of Materials in Civil Engineering，2007，19（5）：385.

［20］Williamson G R.The effect of steel fibers on the compressive strength of concrete［J］.American Concrete Institute，1974（1）：195－207.

［21］Halpin J C，Kardos J L.Halpin–Tsai equations：a review［J］.Polymer Engineering and Science，1976，16：344.

［22］Ahmad H A，Lagoudas C L.Effective elastic properties of fiberreinforced concrete with random fibers ［J］.Journal of Engineering Mechanics，1991，117（12）：2931.

［23］阳知乾，刘建忠.不同纤维对砂浆的抗冲击性能影响［J］.混凝土，2010，2（2）：109.YANG Zhiqian，LIU Jianzhong.Effect of different fibers on the impact resistance of fiber reinforced mortar ［J］.Concrete，2010，2（2）：109.

［24］陈宏友.聚丙烯纤维混凝土力学性能室内试验研究［J］.中外公路，2005，25（1）：91.CHEN Hongyou.Laboratory test of the mechanical properties of polypropylene fiber reinforced concrete［J］.Journal of China and Foreign Highway，2005，25（1）：91.

［25］Piggott M R，Harris B.Compression strength of carbon，glass and Kevlar－49 fiber reinforced polyester resins ［J］.Materials Science，1980，15（10）：2523.

［26］Lo K H，Chim E S M.Compressive Strength of unidirectional Composites［J］.Journal of Reinforced Plastics and Composites，1992，11（8）：838.

［27］Chamis C C.Simplified composite micromechanics equations for strength，fracture toughness and environmental effects ［J］.Journal of Advanced Materials，1984，15：41.

［28］Bentur A，Mindess S.Fiber reinforced cementitious composites［M］.［S.l.］：Elsevier Science Publishing Co.，1990.