电动汽车用锂离子动力电池电感主动均衡系统
2013-07-30戴海峰魏学哲孙泽昌陈金干
戴海峰,魏学哲,孙泽昌,陈金干
(1.同济大学 新能源汽车工程中心,上海201804;2.同济大学 汽车学院,上海201804;3.上海恒动汽车电源有限公司,上海201804)
电动汽车动力电池成组后,电池单体性能不一致严重影响了电池组的使用效果[1-2].单体电池的差异主要由两方面构成:成组前单体电池初始性能差异及使用过程中差异的放大.为减少单体不一致性在应用中的不良影响,可以针对上述2种因素分别采取相应的措施.
首先,可以通过电池单体分选,减小电池成组前的单体性能差异[3-5].该方法并不能根本解决电池成组的不一致问题.在电池组使用过程中,使用环境的不一致等因素会导致电池性能差异的放大,故需要另外的方法抑制电池一致性变差,这一般通过均衡技术实现.
目前,对锂离子电池均衡有2种方法:一是化学方法,通过电池内部化学反应达到均衡充电的效果;一是物理方法,即采取机械或电子的手段达到均衡的效果[6-13].化学均衡法实际上是使用氧化还原对添加剂实现过充保护,该方法目前还未能得到广泛应用.物理方法根据是否有能量损失又分为被动均衡和主动均衡2种.被动均衡一般采用旁路放电电阻实现对高电量的电池放电使其跟模块中具有最小电量的单体保持一致,该方案结构简单,容易实现;但由于每个单体并联一个放电电阻,从而损耗电能并产生热量,给电池系统热管理提出了更高要求.主动均衡通过储能原件实现不均衡电池间的能量转移.这类方案普遍结构复杂,硬件成本高,对系统的可靠性设计也提出了较高的要求;但其能量利用率较高,是目前电池单体均衡研究的一个热点.根据所采用的储能原件不同,主动均衡主要分为电容均衡、变压器均衡以及电感均衡三类.本文基于电感均衡的原理研究了电动汽车用动力电池单体的均衡方案.
1 均衡电路基本结构及原理分析
所设计的电感均衡电路基本结构如图1所示.图中,Q1-Q4为控制均衡过程的场效应管(MOSFET),D1D4为续流二极管,C1-C4为滤波电容,L1-L4为均衡电感.其基本原理为:通过相应的开关控制,将高单体荷电状态(SOC)电池的多余能量存储到电感中,并通过电感将能量转移到低SOC电池中.该方案中,电感只能为相邻的单体电池传递能量.因此,若要给由n节电池构成的电池组均衡,至少需要使用n-1个电感.虽然电感数量较多,但由于电路功率较小、工作频率较高,因此电感的体积较小,均衡电路的体积也较小,结构紧凑.

图1 电感均衡电路Fig.1 Primary balancing schematic
单体电池的电感均衡过程可以分为2个步骤:①高SOC单体电池对电感充电;②电感对低SOC电池放电.为了说明该电路的工作原理,这里假设图1中的电池1为SOC较高单体电池,电池2为SOC较低单体电池,均衡电路将电池1的部分电量转移到电池2中,以使2节单体电池电量平衡.
1.1 高SOC单体电池对电感充电过程分析
闭合开关Q1,断开开关Q2,此时电池1、开关Q1和电感L1构成闭合回路,电池1给电感L1充电,流过电感的电流不断上升,同时电感中存储的能量也不断增加.在这个过程中,电路可以用图2的等效电路替代,图中,Ro为整个回路的等效直流电阻,V1为电池1电池电压,L为储能电感,i为均衡电流.

图2 电感充电等效电路Fig.2 Equivalent circuit during charging of inductance
为计算电感所存能量,要先计算出等效电路中的电流.根据基尔霍夫定律,可得如下方程:
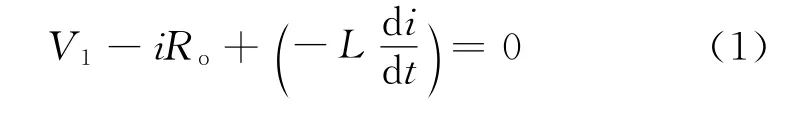
整理可得

式中,t为电感充电持续时间.
1.2 电感对低SOC单体电池放电过程分析
开关Q1,Q2都处于断开状态,电感中的电流保持原有方向,与电池2和D2构成回路开始放电,能量随之下降,同时对电池2充电,如图3所示.
初始时,电感的电流初始值I0为上一过程的电流终值,V2为电池2的电压,Vf为二极管的导通电压.该过程的持续时间取决于D2的导通时间,即加载到D2上的正向电压,当此电压大于导通电压,则回路稳定维持导通;当此电压小于导通电压,则回路截止,此过程终止.而加载在D2上的电压则取决于电感中电流的变化率.因此,电感中的电流是此过程的关键参数.
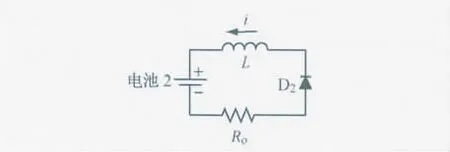
图3 电感放电等效电路Fig.3 Equivalent circuit during discharging of inductance
通过基尔霍夫定律根据式(3)计算电路的电流变化:

整理可得

2 均衡电路设计及主要元件选择
在图1的电感均衡方案中,以任意相邻2节电池均衡为例说明电路的设计及主要元件的选择.
2.1 系统输入输出参数
由于单体电池串联电压均值约为3.3V,因此,对于任意单节均衡电路,输入直流电压VDC可设为3.3V,如设计均衡电流为Io,则输出最大功率为

考虑系统效率Eff,则任意单节均衡电路的输入功率Pimax为

2.2 占空比和开关频率
由于均衡电路开关频率较高,为减小电感磁复位和开关管损耗,提高效率,系统设计工作于断续电流模式(discontinuous current mode,DCM);同时考虑到电感放电回路中二极管导通压降的存在,电感剩余能量不能完全耗尽,易引起电感饱和,因此这里取占空比D为30%.而开关频率与电路元件尺寸以及电路功耗有关.频率越高,电路元件体积尺寸可减小越多,但考虑到电路中的MOS管和二极管的功耗,系统开关频率取200kHz.
2.3 电感参数
若忽略电感充电回路中的等效串联电阻Ro(约为0.01Ω),并忽略电感并联电阻上消耗电流(约为1%以下),则充电均衡电流为

式中,f为开关频率.那么通过电流预设值ic和D可计算出均衡电感L.

式中,Vc为均衡单体电池电压.
2.4 高频滤波电容
为了保证均衡电流达到设计峰值,就必须在均衡过程中给充电回路提供稳定的充电电压,而滤波电容就可起到稳压滤波的作用.该电容值的确定需要采用迭代的计算方法得到.首先,忽略均衡过程中电压纹波,并计算此状态下的均衡电流平均值ia.

式中:ipeak为均衡峰值电流;Ton为开关导通时间;Tp为开关周期.
根据电容的定义可知,电容的电压纹波Δu与电容接受/释放的电量ΔQ有关.
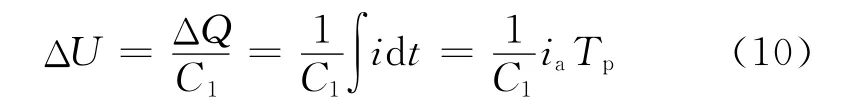
式中,C1为高频滤波电容.
在均衡过程中,需要限制充电电压的纹波,一般要求电压纹波ΔU小于10mV.将各个参数代入式(10)可得

为了进一步提高电压稳定性,电容C1可适当放大.若所设计出的稳压滤波电容值过大,则应重新设置最大均衡电流值,并迭代计算电容.
2.5 电感并联电阻的选择
由于在电感放电过程中,L1与C2构成了LC串联振荡电路,电池2的电压也随着振荡,为了消除振荡引起的不利影响,在电感两端并联一小电阻,如图1中的R1和R2构建阻尼环节.该电阻值对整个系统的工作效率有较大影响,若设置过小,虽然可以加快振荡衰减过程,但同时在电感充放电过程中消耗过多能量;若设置过大,虽然可以保证电感充放电的能量利用率,却不能实现阻尼作用.通过仿真获取兼顾两者的平衡点.
对所设计的系统选择电感两端并联2kΩ电阻后进行仿真,如图4.均衡电流在整个过程中保持稳定,在每次电感放电结束后电流都能迅速衰减到零.在均衡过程中,流过2kΩ电阻的电流最大值为3 mA,只占整个均衡电流的0.25%,均衡能量损失很小,对均衡效率影响不明显.
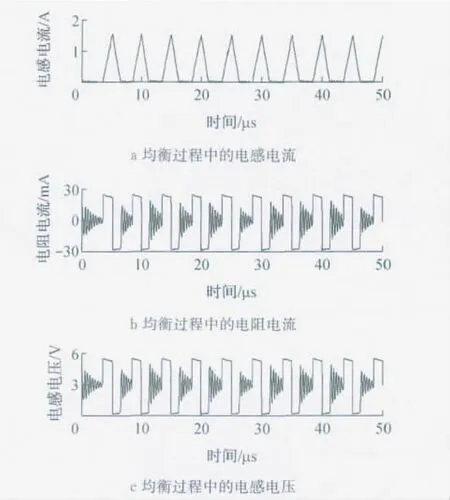
图4 电感剩余能量消耗仿真Fig.4 Simulation of residual energy consumption on inductance
2.6 MOSFET管和二极管的选择
开关器件MOS管的选择可从漏源极击穿电压、持续漏极电流、开关延时和导通电阻等方面来考察.均衡电路中的电压需求为2节单体最大电压之和,即电压等级应该在10V以上;考虑到均衡电流尖峰可能较大及以后增大均衡电流的可能性,电流等级应该在10A以上;开关延时表征开关是否迅速开关,其值越小开关越迅速,功耗越小,发热越小,故应该选择开关延时较小的MOS管;为了减少回路中的功率损耗及防止MOS管发热,应该选择导通内阻比较小的MOS管.
而就构成电感放电回路的二极管而言,应具备如下特性:导通阻抗小,减小电能消耗,同时降低系统温升;导通压降小,使电感电能尽可能多地释放给电池;响应速度快等.
3 电感主动均衡电路的仿真及优化
对图1所示的设计电路图进行仿真.仿真工具采用LINEAR公司提供的模拟软件LTspice IV.参照图1电感主动均衡电路,利用LTspice IV设计如图5所示的电感主动均衡仿真电路图,图中,D2s为续流二极管,V1,V3分别模拟相邻电池电压,L1为均衡电感,R4为并联电阻,M1为控制均衡 MOSFET,R1为MOSFET栅极放电电阻,D1s,R2用于使电容C1s端电压迅速回零,C1s用于驱动信号隔直,V2为MOSFET驱动信号.尽管仿真中仅设计了一路均衡电路,但由于其他几路工作情况相同,因此,在通过仿真确定一路的参数后,其他几路参数可类似地分析计算.仿真时用3.2V恒压源V1,V3代替真实的单体电池,用电压源V2输出脉冲信号代替脉宽调制(PWM)的控制,输出0~5V方波.
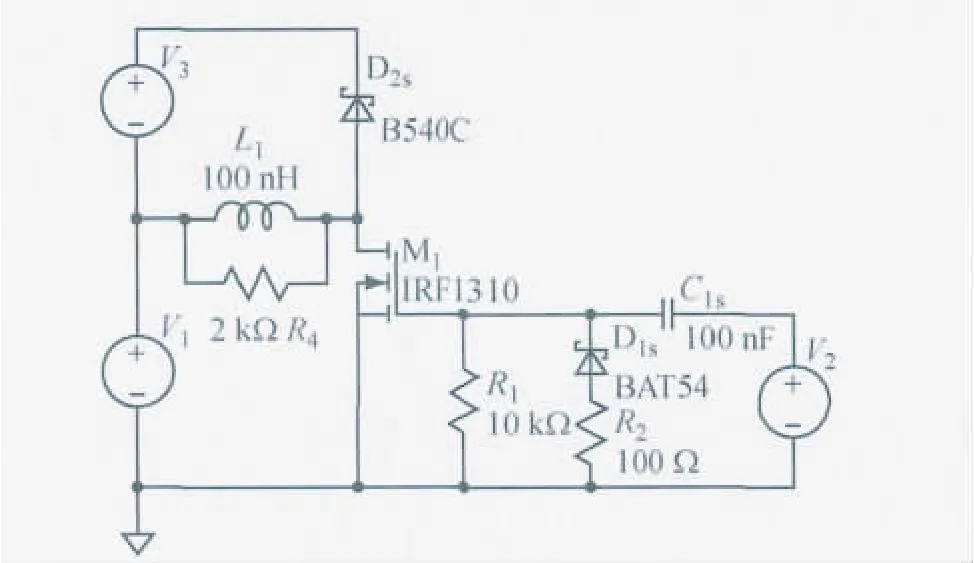
图5 电感主动均衡仿真电路Fig.5 Simulation of the active balance schematic
由于MOS管门极(G端)和源极(S端)之间寄生电容的存在,在MOS管开启时,先给寄生电容充电,电容的电压缓慢上升,故MOS管的开启速度变缓;当MOS管关断时,寄生电容放电,但电容电压下降缓慢,故MOS管的关断速度亦变缓,这样使得MOS管开关延时大大增加.而MOS管开关延时期间会有均衡电流流过,这增加了MOS管的功率损耗,不仅影响均衡电路的效率,且使MOS管发热,影响其使用寿命.为了解决这一问题,在MOS管G端与S端间并联一个放电电阻R1.从解决MOS管开关延时的角度来说,该电阻越小放电越快,MOS管关断越迅速.但如果电阻过小,电容C1端的电荷通过R1迅速放掉,使得控制电压迅速下降,MOS管导通不完全,同样导致MOS管功率损耗增加.通过仿真,权衡R1取10kΩ时能比较好地解决上述2种情况.
二极管D1s的作用是使电容C1s两端的电压迅速回零,保证控制信号的幅值在0~5V之间变化.当没有电阻R2和二极管D1s时,MOS管G端的控制波形如图6所示,控制信号曲线有负电压出现,而且幅值越来越小.究其原因,电容C1两端的电压不能突变,如当C1左边的电压下降至2.5V,此时C1右边电压由5.0V下降至0V,由于电容两端电容不能突变,电容左边电压也下降5.0V,这时C1s左边电压降至-2.5V.而有电阻R2和二极管C1s时,一旦出现负电压D1s导通,D1s和R2提供一个放电的通道,负电压通过R2放电,电压迅速归零,否则如果电压不能迅速回零,将会出现MOS管开启电压不够的情况.
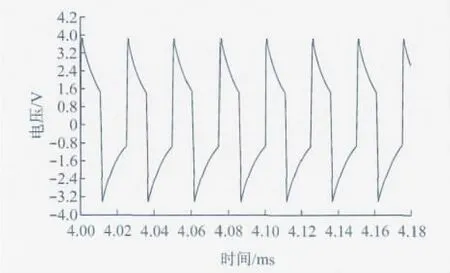
图6 无二极管时的MOS控制端电压Fig.6 Gate control voltage of MOS without the diode
图7 是各个元件通过参数优化后的仿真结果.可以看出控制波形虽然有变为负电压的现象,但是幅度很小,而且能迅速回正,所以它不会引起控制信号电压幅值减小,从而保证MOS管的正常开启和关断.工作电流曲线为三角波,且跟控制波形保持同步,即当MOS管开启时,电流上升,电池给电感充电;当MOS管关闭时,电流下降,电感给电池充电.

图7 电路优化后的仿真结果Fig.7 Simulation results after optimization
4 电感主动均衡试验
以12节串联8Ah磷酸铁锂(LiFePO4)电池模块为对象,测试上述电感主动均衡方案的效果.
4.1 电流测试结果及分析
在均衡过程中观察单体电池的均衡电流,图8所示是电感的工作电流,该图利用示波器电流探头测得,电流探头的比例为100mV·A-1,本文所有试验均是采用此比例.可以看出,电感充电电流的最大值是1.770A,充电周期平均电流值约为0.469 A,放电周期平均值约为0.339A,电感工作电流周期平均值为0.833A.电流曲线为三角波,曲线的上升阶段是单体电池向电感转移能量的过程,即电感的充电过程,曲线的下降阶段是电感向单体电池转移能量的过程,即电感的放电过程,从而实现了能量单体之间的转移.在能转移过程中,可估算出该电感主动均衡方案的效率η.

式中:U1,U2分别为低侧、高侧电池单体电压;I1,I2分别为电感放电、充电电流峰值;T1,T2分别为电感放电、充电时间;Iavg1,Iavg2分别为电感放电、充电周期平均电流.
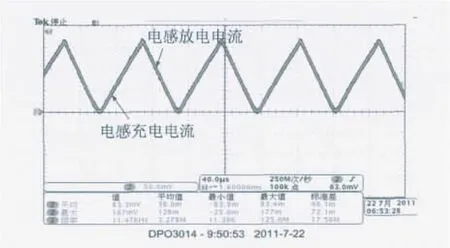
图8 均衡中的电感电流Fig.8 Working current of inductance during balancing
以上的电流分析均基于单路均衡开启时的工作电流,实际应用中可能出现某个单体电池电压高而相邻单体电池电压均低或是某个单体电池电压低而相邻电池电压均高的情况.在这2种情况下需开启双向均衡,也就是让高电压单体电池给相邻的低电压单体电池同时充电,或让相邻的高电压单体电池同时给低电压单体电池充电.在这种情况下,所提方案均衡时转移的能量约是单向的2倍,增加了均衡的效果,缩短了均衡时间.以图9、图10来分析上述2种特殊的均衡方式.
图9是以双向充电(相邻的高电压单体电池同时给低电压单体电池充电)时低电压单体的充电电流曲线.从图可见,在1个充放电周期中电流曲线左侧以电流的向上跳变点为分割点将曲线分成左右两部分,前半部分为单个电感的充电电流曲线,能量存储在电感中,并未给其他单体电池充电;后半部分的电流向上发生了一个跳变,这是由于另一个电感也在存储能量,此时的电能相当于2个电感上的能量的叠加.电流曲线的右侧则是储存在2个电感上的能量给低电压单体电池充电的过程.平均电流可达1.150A,大大增加了均衡电流,缩短了均衡时间.

图9 双向充电均衡电流Fig.9 Balancing current during bi-directional charging
图10 是以双向放电(高电压单体电池同时给相邻的低电压单体电池充电)时低电压单体的充电电流曲线.可以看出,在1个充放电周期中,电流曲线左侧是高电压单体电池给相邻的2个电感放电的过程,能量存储在2个电感中;电流曲线右侧以电流的向下跳变点为分割点将曲线分成左右两部分,这两部分分别是2个电感放电给相邻的低电压单体电池充电的过程.该双向放电的过程平均电流达到1.330 A,远大于单个电池充放电的平均电流.
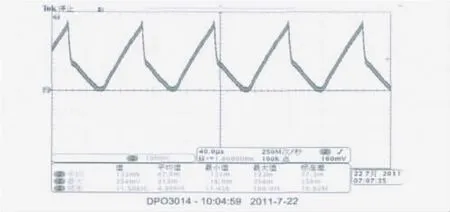
图10 双向放电均衡电流Fig.10 Balancing current during bi-directional discharging
4.2 电池均衡效果分析
为了更清楚地研究分析均衡电路的效果,试验前对单体电池电压进行调节,使整个模块存在一个较大的压差.各个单体电池起始电压及其电压分布情况如图11a所示.可以看出,电池模块中存在偏离平均电压的过高单体和过低单体.其中最高单体电池电压值为3.075V,最低单体电压值为2.950V,其压差为125mV.
均衡结束后的单体电池电压分布如图11b所示.对模块单体电池电压进行分析,最高单体电池电压为3.015V,最低单体电池电压为3.003V,其压差为12mV,可认为此次均衡结束.从图11可以看出,该电感主动均衡方案效果明显,能使得一个模块中参差不齐的电压分布均衡值相同.
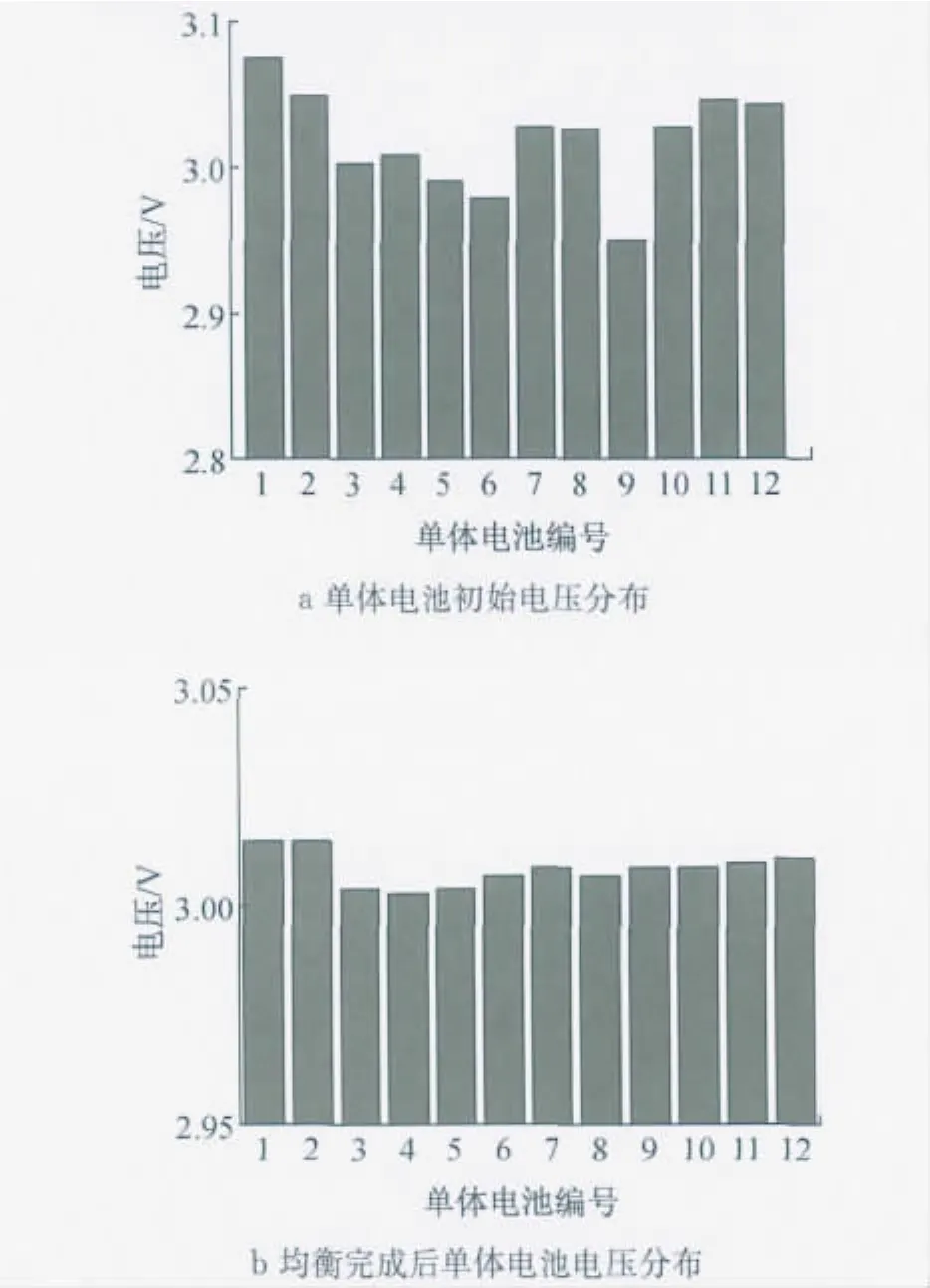
图11 均衡前后的单体电池电压分布Fig.11 Battery voltages before/after balancing
图12 是在均衡过程中各个单体电池电压的变化曲线.可以看出,所有单体电池电压不断趋于平均值.跟被动均衡电压曲线不同的是,对于电压偏高的单体,通过释放能量逐渐趋于均值,对于电压偏低的单体,通过吸收能量逐渐趋于均值.电感主动均衡电压走势呈现如“>”型,说明在电感主动均衡过程中高电压单体通过电感把能量转移到低电压单体,而非使能量耗散,提高了均衡效率.
试验结束后,单体电池的最高和最低电压趋于平均值.总电池的平均电压略有下降,从3.020V降至3.010V,降幅约为10mV,说明该电感主动均衡方案仍然有电能损耗,主要是因为均衡回路中电感和MOS管等器件存在着阻抗.通过深入研究可采取一些优化措施,如采用软开关技术或优化系统参数以进一步提高系统均衡效率.

图12 均衡过程中单体电池电压变化Fig.12 Cell voltage variations cells during balancing
5 结论
针对电动汽车用锂离子动力电池单体不一致问题,研究了一种基于电感式的主动均衡方案.由于电路功率较小、工作频率较高,因此电路体积较小,结构紧凑,连线简单,易于模块化设计,便于系统拓展.详细研究了系统的设计、仿真及参数的选择、优化,着重分析了频率、占空比、电感参数、滤波电容、电感并联电阻等参数的选择对系统性能的影响.采用12节磷酸铁锂电池组成模块进行均衡方案测试验证,分析均衡过程中的电流及效率,并比较了均衡前后电池的一致性,结果表明,该方案具有较好的均衡效果,测试过程中相邻单体间的均衡效率可达到72%左右.尽管本方案已得到初步验证,但仍需要完善,如进一步提高系统效率、增大均衡电流以适应更大容量电池使用需求以及均衡系统的可靠性措施等方面仍需作深入研究.
[1]麻友良,陈全世.混合动力电动汽车用蓄电池不一致的影响分析[J].汽车电器,2001(2):5.MA Youliang,CHEN Quanshi.The inconsistent influence analysis of battery for hybrid electric vehicle[J].Auto Electric Parts,2001(2):5.
[2]王震坡,孙逢春,林程.不一致性对动力电池组使用寿命影响的分析[J].北京理工大学学报,2006,26(7):577.WANG Zhenpo,SUN Fengchun,LIN Cheng.An analysis on the influence of inconsistencies upon the service life of power battery packs[J].Transactions of Beijing Institute of Technology,2006,26(7):577.
[3]多智华,李革臣,张殿龙.一种快速实现波形识别的电池分类算法[J].哈尔滨理工大学学报,2001,6(4):52.DUO Zhihua,LI Gecheng,ZHANG Dianlong.A fast algorithm based on curve recognition for cells classification[J].Journal of Harbin University of Science and Technology,2001,6(4):52.
[4]申建斌,唐有根,李玉杰,等.无监督聚类在锂离子电池分类中的应用[J].计算机与应用化学,2007,24(3):305.SHEN Jianbin,TANG Yougen,LI Yujie,et al.A new method based on unsupervised clustering for lithium-ion battery classification[J].Computers and Applied Chemistry,2007,24(3):305.
[5]Kim Jonghoon,Shin Jongwon,Chun Changyoon,et al.Stable configuration of a li-ion series battery pack based on a screening process for improved voltage/SOC balancing [J].IEEE Transactions on Power Electronics,2012,27(1):411.
[6]吴友宇,梁红.电动汽车动力电池均衡方法研究[J].汽车工程,2004,26(4):382.WU Youyu,LIANG Hong.A study on equalization charging for EV traction battery[J].Automotive Engineering,2004,26(4):382.
[7]CAO Jian,Schofield N,Emadi A.Battery balancing methods:a comprehensive review [C]//Proceedings of IEEE Vehicle Power and Propulsion Conference.Harbin:VPPC,2008:1-6.
[8]Stephen W.Moore,Peter J.Schneider.A review of cell equalization methods for lithium ion and lithium polymer battery systems[C]//SAE.[S.l.]:SAE,2001:2001-01-0959.
[9]何仕品,朱建新.锂离子电池管理系统及其均衡模块的设计与研究 [J].汽车工程,2009,31(5):444.HE Shipin,ZHU Jianxin.Design and study of battery management systm and its equalization module for Li-ion batteries[J].Automotive Engineering,2009,31(5):444.
[10]李红林,张承宁,孙逢春,等.锂离子电池组均衡充电和保护系统研究[J].北京理工大学学报,2004,24(3):210.LI Honglin,ZHANG Chengning,SUN Fengchun,et al.Equalization charging and protection system for li-ion battery series [J].Transactions of Beijing Institute of Technology,2004,24(3):210.
[11]杨春雷,刘志远.一种电动汽车动力电池均衡控制方法的设计[J].上海交通大学学报,2011,45(8):1186.YANG Chunlei,LIU Zhiyuan.Equalization control method design for power batteries in an electric vehicle[J].Journal of Shanghai Jiaotong University,2011,45(8):1186.
[12]Einhorn M,Guertlschmid W,Blochberger T,et al.A current equalization method for serially connected battery cells using a single power converter for each cell[J].IEEE Transactions on Vehicular Technology,2011,60(9):4227.
[13]罗玉涛,张智明,赵克刚.一种集散式动力电池组动态均衡管理系统 [J].电动技术学报,2008,23(8):131.LUO Yutao,ZHANG Zhiming,ZHAO Kegang.A novel distributed equilibrium and management system of dynamic battery pack[J].Transactions of China Electrotechnical Society,2008,23(8):131.
