房产销售价格变化与物价水平的动态效应分析

张 丽

（洛阳师范学院数学科学学院统计系，河南洛阳 471022）

1 问题的提出

从经济学角度，不管居民是花钱买房还是租房都可看作消费，而房屋销售并未纳入居民消费价格指数CPI的核算中，住房列入了固定资本的形成范畴。但是在CPI数据中含有调查居住类的项目，比如木材、水泥及水、电、天然气等能源的花费，这与反映生产原材料的价格变动的工业品出厂价格指数PPI共同体现了当前物价水平变化情况。由此可见，房价波动与居民的消费水平及生产成本密切相关，了解房产销售价格指数波动的特征，有必要分析房产销售价格与物价水平间存在的关系。

目前国内的学者对相关问题做了研究，吕莜萍[1]从土地价格、商品房价格及二手房价格之间的传导机理,分析了我国房地产市场的定价模式及不同趋势中市场参与者的交易行为,揭示了我国房地产市场价格变动的内在机制。李运蒙[2]运用向量自回归模型及脉冲响应函数对2007年1月至2010年6月居民中长期消费贷款和房屋销售价格指数月度统计数据之间的波动传导关系进行了研究。龙海明[3]选择1999～2008年的土地交易价格指数与房屋销售价格指数季度数据，通过建立VAR模型进行实证分析，研究表明房价对地价的影响高于地价对房价的影响。本文将2005年7月至2010年12月的商品房销售价格指数视作随机时间序列，通过分析价格序列间的动态变化规律，建立向量自回归模型，在统计分析基础上对短期内的未来房地产价格走势进行判断。

2 模型分析

2.1 VAR模型

向量自回归是从数据特征出发，将系统中的每一个内生变量作为模型中所有内生变量滞后项的函数来建立模型，从而将单变量自回归(AR)推广到多变量的时间序列分析中。常用于解释经济系统中多变量序列之间的动态变化规律，其模型形式为

其中，Yt是m维内生变量向量；Xt是n维外生变量向量；T是样本个数；Ai与Bi分别是待估的参数矩阵，p，q分别是模型中内生变量与外生变量的滞后期阶数；εt是独立同分布的随机扰动项。

具体地，三维滞后一阶的模型为

Y1t=α10+Φ11Y1t-1+Φ12Y2t-1+Φ13Y3t-1+ε1t

Y2t=α20+Φ21Y1t-1+Φ22Y2t-1+Φ23Y3t-1+ε2t

Y3t=α30+Φ31Y1t-1+Φ32Y2t-1+Φ33Y3t-1+ε3t

2.2 变量选取与数据说明

本文将采用房地产价格指数(EPI)作为度量房产销售价格的指标，以居民消费物价指数(CPI)作为物价水平与通货膨胀的度量指标，工业品出厂价格指数(PPI)作为企业原材料生产成本的度量指标。所有数据均为月度同比指数，选取样本区间为：2005年7月至2010年12月(原始数据来源于中国国家统计局网站)，实证分析的数据均采用计量统计软件Eviews6.0运算处理得到。建立工作文件，绘制样本序列数据的时序图及相关关系初步判断原序列非平稳，则对序列做ADF单位根检验，假设原序列具有单位根，分别对如下三个方程进行检验：

∇yt=γyt-1+（序列存在截距项）

∇yt=α+γyt-1+（序列存在时间趋势项）

∇yt=α+δt+γyt-1+（序列存在高阶滞后项）

其中，α为常数项，βi为高阶滞后相关系数，γ=0表示序列为单位根过程，δt为线性时间趋势项，随机扰动项μi为白噪声[4][5]。

分别对仅有滞后项、存在截距项、存在截距与趋势的方程进行平稳性检验，计算出的t统计量均大于1%，5%，10%显著水平下的临界值，对应p值较大，即拒绝原假设犯错的概率很大，故不能拒绝有单位根的原假设，原有CPI序列、EPI序列及PPI序列均为非平稳序列。

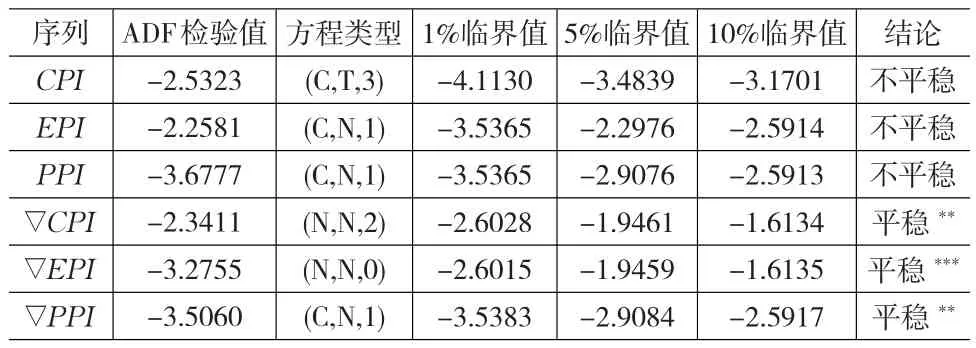
表1 各序列单位根检验的结果

对原始数据做一阶逐期差分后，经表1单位根检验结果可知，差分后的序列为平稳时间序列。说明CPI序列、EPI序列及PPI序列为同阶单整序列，原序列之间可能存在长期稳定的比例关系，满足协整检验的条件，可以进一步建立VAR模型。

2.3 Granger因果检验与协整检验

格兰杰因果检验考察不同序列之间是否互为Granger成因，主要表现在解释变量序列的滞后项的引入能否对目标变量的解释有显著影响。即引入A序列的滞后值有助于提高B序列的被解释程度，则A序列是B序列的Granger成因。格兰杰因果检验对变量序列的滞后项很敏感，通常需对不同的滞后期进行检验。

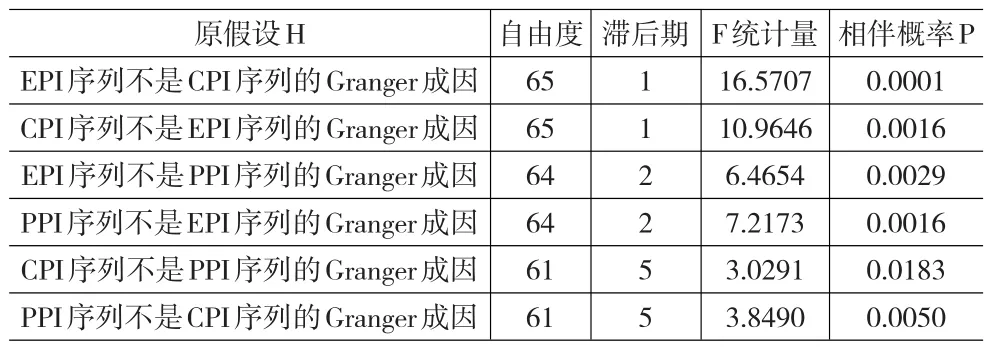
表2 格兰杰因果检验结果

经表2检验结果可知，在5%的显著水平下，各原假设在不同的滞后期被拒绝，表明EPI与CPI序列及PPI序列之间存在较强的因果关系，房产价格的波动存在理性预期，消费价格水平及生产成本对房产价格的影响比较直接，而生产成本与消费价格水平之间的影响实效较长。各序列间互为Granger因果关系，具有双向的反馈关系，适合建立三变量序列的VAR模型。

2.4 模型估计

VAR模型建立的关键问题是对变量相互影响的最大可能滞后阶数进行判断。滞后期太小，不能够充分提取信息以完整反映变量间动态关系；而滞后期过长将导致待估参数增多，模型复杂且过度损失自由度，进一步会影响参数估计的有效性。实践中，往往利用三个序列之间的互相关关系（如图1、图2、图3）对滞后期进行初选。充分考虑三组变量序列滞后项与超前项之间滞后期的平衡，取足够大的滞后期以充分提取信息，从(3,1),(0,3),(0,1)中预选滞后3期进行模型估计。

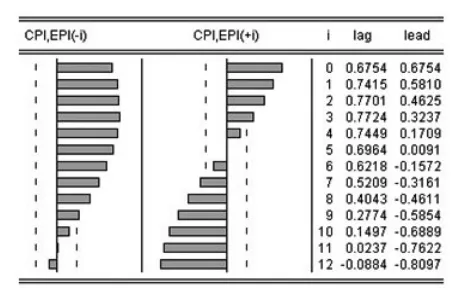
图1 CPI序列与EPI序列的互相关图

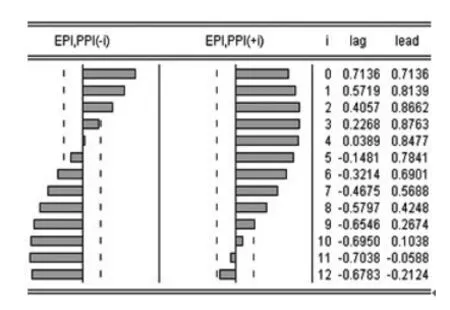
图2 EPI序列与PPI序列的互相关图

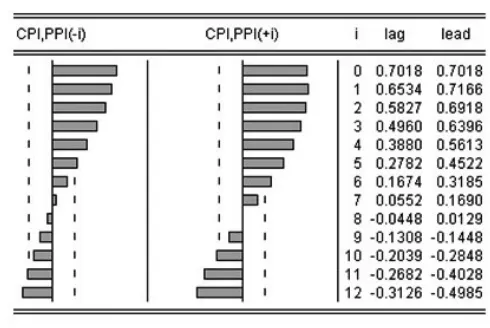
图3 CPI序列与PPI序列的互相关图

图4 VAR模型稳定性检验根模图

另外，结合LR检验统计量、AIC信息准则、SC信息准则、HQ信息准则以及最终预测误差FPE，对模型进行评价，具体计算方法为

其中T为样本个数，k为模型中待估参数的个数，p为VAR模型的最佳阶数，为残差方差的极大似然估计值，LogL为模型参数的对数似然估计值，表达式为

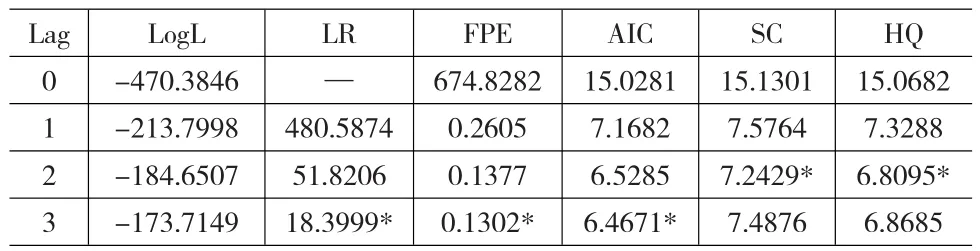
表3 VAR模型滞后阶数的选择指标

从模型的评价指标结果(表3)看出，多数指标集中在Lag=3阶时取值最小，Lag=2的SC准则及HQ准则为最小值，主要取决于SC信息准则对模型参数的惩罚力度比较大；以信息提取充分为前提，选取众数为原则，最终确定VAR模型的最大滞后阶数为3阶。随着滞后期加长，模型的稳定性会下降，因此结合滞后3阶的VAR模型稳定性检验根模图(图4)进行检验。被估模型的所有特征根的模都落在单位圆内，所以系统满足状态稳定的条件，建立VAR(3)模型合理有效。

进一步判断CPI序列、EPI序列及PPI序列之间是否存在稳定的动态关系，在滞后3期，假定模型含有无约束的截距项条件下，对序列的协整关系进行检验。

从Johansen检验基于极大似然估计的迹统计量检验结果表明（见表4），在5%的显著水平下拒绝原假设，说明CPI序列、EPI序列及PPI序列存在长期均衡的协整关系。

表4 迹统计量协整检验结果

综合以上检验结果，对样本数据建立模型，经参数估计得VAR(3)模型具体形式为

从方程估计结果看出，EPI序列滞后一期对自身的影响系数为1.126，滞后二期、三期的系数都比较显著，说明房产销售价格受自身序列波动的影响很强，当期的价格体现了过往三期的水平。

2.5 脉冲响应与方差分解

向量自回归模型的脉冲响应函数与方差分解分析，可以表现不同序列对冲击做出的动态反应路径。脉冲响应函数刻画误差变动在系统内传递的动态过程，即随机扰动项上加一个一次性的冲击对于内生变量当前和未来取值将带来怎样的影响。

图5 脉冲响应结果

图5中实线表示各序列对于一个标准差新息的脉冲响应，随着预测期数的增加所显示出的变化路径。虚线表示脉冲响应的两倍标准差置信域。结果表明，CPI序列、EPI序列及PPI序列均对自身扰动的反应很敏感，在面临一次偶然的上涨时，会拉动其后几个月的较大幅度的增加，特别是EPI序列的增幅甚至达到高位后，缓慢回落。说明房产价格指数受自身变化趋势的影响直接且效果持续性强，房价调控的过程必然是长期的。

EPI序列对CPI序列的脉冲响应存在持续较小的正影响，即当期给消费价格指数一个正的冲击，房产价格指数会有微小的反应，并很快衰减至零。而EPI序列对PPI序列的脉冲响为负影响，生产价格指数当期受到一个标准差的冲击，初期对房产价格指数没有明显影响，之后逐渐呈稳定的负响应。而CPI序列对生产成本指数的冲击比较敏感，有持续递增、逐渐放大的负影响。可见，EPI序列物价水平变化的影响存在一定的时滞性，但其影响效果不大。

方差分解的基本思想是将系统中各个内生变量的波动按其成因分解成与随机扰动项相关的各组成部分，从而了解每一个结构冲击对模型内生变量的相对重要性。其目的在于搞清楚系统的一个变量受到结构冲击后，以变量预测误差百分比的形式反映变量之间的交互程度。

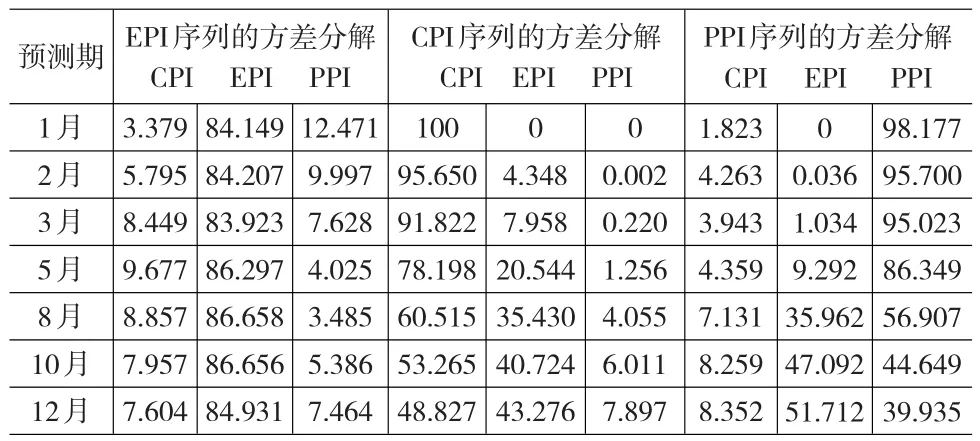
表5 各序列方差分解结果

方差分解的结果见表5，根据方差分解的结果：

首先，EPI序列中的随机新息当期直接影响EPI，且通过当期影响传递到后期。EPI序列对自身的影响始终保持着较高贡献率(大于84%)，滞后期越短，房产销售价格指数的自身解释能力就越强，可见房价的上涨通常在短期内很难得以复位。CPI及PPI序列对房产价格的影响始终没有成为主力，消费价格的冲击存在10%以内的影响，而生产成本的上涨在前两月内对房价有较明显的波动，其后的时间有逐步的纠正，影响控制在10%以内。说明整体物价水平的变动会对房价形成冲击，但影响有限。即便是建筑原材料生产价格的变动对房价的冲击作用仍然是可控的，由此可见，房价自身的推动作用远大于市场物价水平的影响作用，所以房产销售价格波动的决定因素不是物价水平，更多的来源于房产市场的供求关系及房产销售政策的导向力量。

其次，CPI序列与PPI序列尽管在初期对自身的贡献程度极高，但经系统传递后到第十二期影响均降至50%以下。相比之下，房产价格指数的变动对物价水平的的影响却十分显著，EPI序列对CPI序列与PPI序列的贡献程度分别达到43.276%与51.712%，说明EPI序列的变化对物价水平波动的冲击是长期而稳定的。房产价格的上涨必然在带动消费价格水平的上涨，并将在其后一段时间内推动生产成本价格一定程度的上涨。从长期来看，控制房产销售价格上涨幅度对稳定整个经济社会的物价水平有着很重要的作用。

2.6 模型预测

利用所估计的VAR(3)模型对EPI进行预测，扩展数据样本期为2005年7月至2011年12月，通过运行Eviews6.0，采用动态预测方法，计算得到2011年共计12期的房产销售价格指数预测值。表6预测结果表明，与上年同期相比，在2011年间房产销售价格指数EPI将呈现逐渐回落的趋势。

表6 2011年EPI动态预测值

3 结论

从统计数据上看，房产销售价格指数与物价水平的变动呈现相同的变化趋势，协整分析表明其具有长期均衡的关系。Granger因果检验结果表明，从数据特征上房产销售价格序列与CPI序列与PPI序列具有显著的双向可释性。从脉冲响应函数与方差分解的分析结果来看，房产销售价格指数对自身的变动很敏感，受CPI序列与PPI序列的影响较稳定。而物价水平变动与房产销售价格水平的相互影响程度并不对等，房价受物价水平引导的因素并不强，而物价的变动程度却受房产价格变动影响长久，所以说稳定物价必须关注房产销售价格的变化趋势。市场物价的波动对房产价格的冲击是有限的，房地产价格上涨更多的是过往自身价格水平的体现。

房产价格波动主要来自房地产市场的供求不平衡，一方面，普通房源供应不足而圈地、囤地现象存在；另一方面，住房的刚性需求推动与改善性、投机性需求的助长。同时，随着消费价格与生产资料价格水平的不断攀升使得房价预期明显增加，各方面因素均为房价上升提供了空间。因此，房价调控应切实抓好保障住房的建设，规范房地产市场管理，依法查处恶意炒作、哄抬房价等扰乱市场秩序的行为，以促进房产市场长期稳定的发展态势。

[1]吕莜萍.我国房地产市场价格传导机理及效应分析[J].价格理论与实践,2011,(5).

[2]李运蒙.房产市场风险与银行信贷风险传导的时滞分析[J].统计与决策,2011,(5)．

[3]龙海明,郭微.基于VAR模型的我国房价与地价动态计量分析[J].经济数学,2009,(6)．

[4]高铁梅.计量经济分析方法与建模[M].北京:清华大学出版社,2009,（5）.

[5]Harvey,A.C.The Econometric Analysis of Time Series[M].New York:Wiley,1981．