几何分布冷贮备产品的统计分析

徐晓岭，王蓉华，应晶晶，顾蓓青

(1.上海对外贸易学院商务信息学院，上海 201620；2.上海师范大学数理学院，上海 200234)

1 几何分布冷贮备系统产品简介

设冷贮备系统产品由2个单元组成，产品在初始时刻，一个单元开始工作，另一个单元作冷贮备。当第一个单元失效时，贮备单元去替换，直到贮备单元失效时，产品就失效。所谓冷贮备是指贮备单元不失效也不劣化，贮备期的长短对以后使用时的工作寿命没有影响。此系统可以用图1来表示。

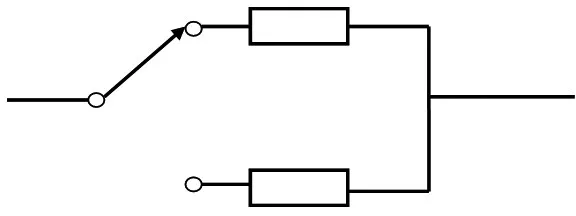
图1 冷贮备系统产品示意图

在工程上，许多单元的寿命分布可用离散型分布来描述，譬如一些开关、插件以及以成功次数作为评价使用寿命的单元等，其寿命就可以用离散寿命分布中的几何分布来描述。由于几何分布无记忆性，使得它是离散寿命分布类中最为重要的，几何分布已广泛应用于信息工程、电子工程、控制论以及经济学等领域。

设离散型随机变量X服从参数为1-q的几何分布，X～G(1-q)，即X的概率分布为：

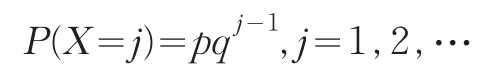
其中0＜q＜1,p=1-q

2 几何分布冷贮备系统产品寿命分布及数字特征

设冷贮备系统产品由两个单元构成，假定产品的两个单元的寿命Y1,Y2同服从参数为q1的几何分布，Yi～G(1-q1)，i=1,2，开关寿命Yk服从参数为q2的几何分布，Yk～G(1-q2)，且Y1,Y2,Yk相互独立。

在初始时刻单元1进入工作状态，单元2工作冷贮备，当单元1失效时，需要使用转换开关，若此时开关已经失效则产品失效。即产品的寿命就是单元1的寿命Y1；当单元1失效时，若转换开关正常则单元2替换单元1进入状态，直到单元2失效，产品就失效，此时产品的寿命是Y1+Y2，于是，产品的寿命X为：

对k≥1，X的分布律为：

对k≥1，X的可靠度函数为：

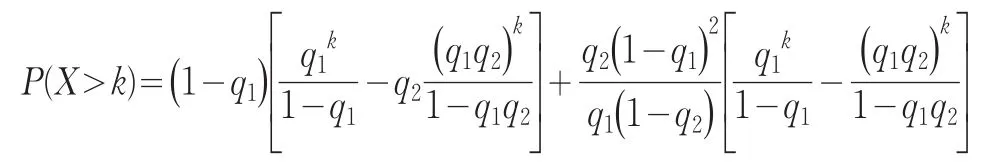
进而，X的均值、二阶矩及方差分别为：

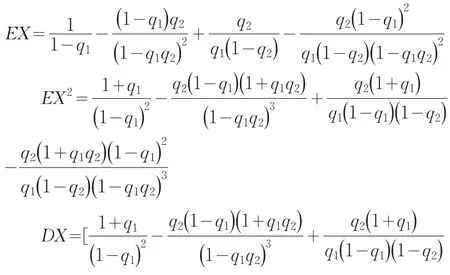
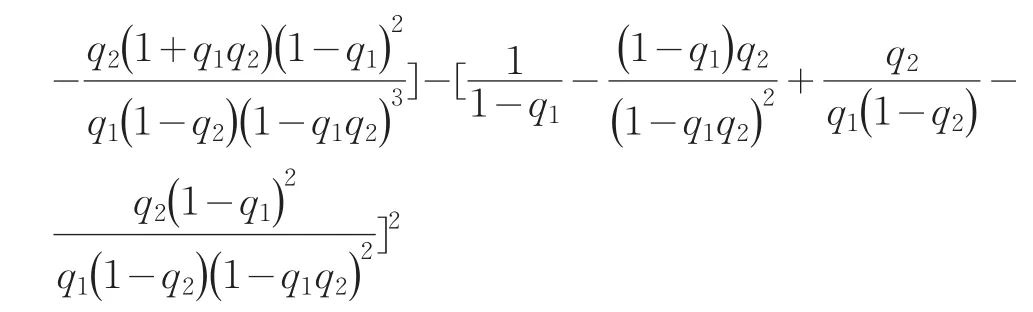
特别地，当q1=q2=q时，

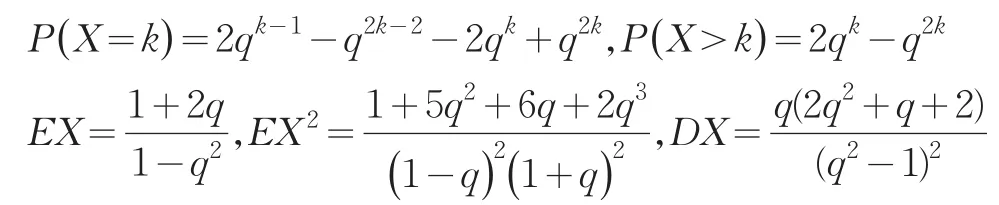
3 几何分布冷贮备系统产品的统计分析

3.1 参数的矩估计

设X1,X2,…,Xn是来自总体X的一个简单随机样本，其样本观察值记为：x1,x2,…,xn.由矩估计思想可列如下方程：

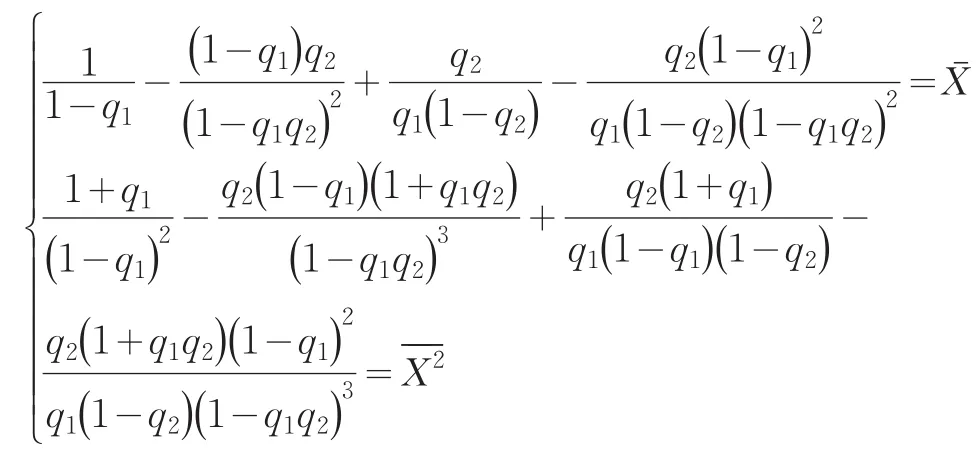
从中可解得参数的矩估计。

化简可得方程：

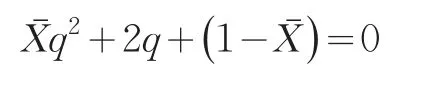
从中可解得参数q的矩估计

3.2 参数的极大似然估计

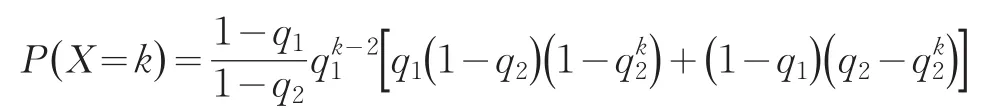
特别地，当q1=q2=q时，

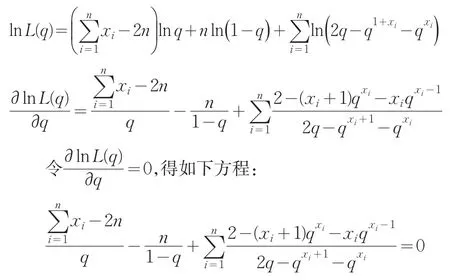
从中可解得参数的极大似然估计q̂。

考察上述方程在q∈(0,1)上解的情况：给定q的真值为0.8，样本容量为20，通过Monte-Carlo模拟产生一组样本，从而给出函数f(q)的图像如下：

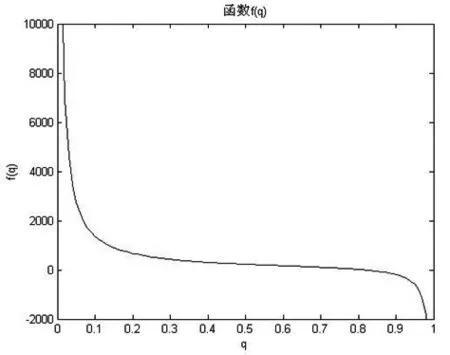
图2 函数f(q)的图像

3.3 参数估计的模拟比较

为比较上述点估计的优劣，采用Monte-Carlo模拟的方法。先固定样本容量n=10(10)40，给定参数p的真值，q1=q2=0.5(0.1)0.9，通过Monte-Carlo模拟产生样本容量为n的一个随机样本，在全样本情况下参数的矩估计和极大似然估计，如此重复1000次计算点估计的均值和均方差，模拟结果列于表1，从中可以看出：（1）对固定的q，q的矩估计和极大似然估计的均方差随n的增大而减小；（2）比较矩估计和极大似然估计的均方差，可得随样本容量的增大，极大似然估计较矩估计相对较小，均值也比较接近真值。因此可以认为：极大似然估计优于矩估计。

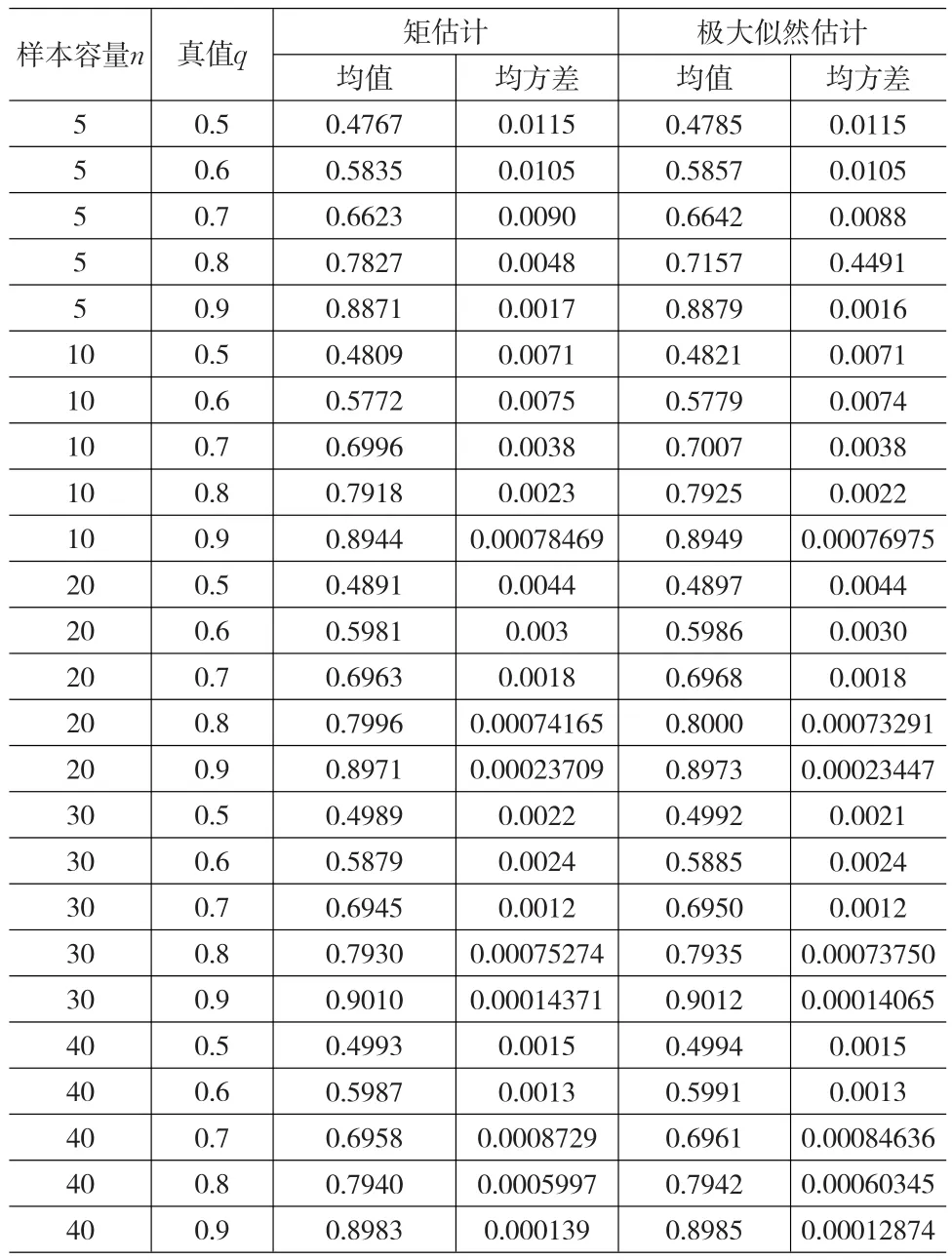
表1 矩估计和极大似然估计的模拟结果

例1：取参数真值为q=0.8，样本容量为n=30，通过Monte-Carlo模拟产生30个随机数如下：9，1，8，7，3，7，7，3，10，3，10，5，1，1，5，10，4，39，6，10，17，4，13，2，10，9，8，11，6，9，利用本文方法可得参数q的矩估计为：q̂1=0.8173；极大似然估计为：=0.8162.

[1]曹晋华，程侃.可靠性数学引论[M].北京：科学出版社,1986.

[2]茆诗松.概率论与数理统计[M].上海：中国统计出版社,2005.

[3]徐晓岭.几何分布和Weibull分布产品的统计分析[D].上海：上海师范大学数理学院，2004.

[4]程侃.寿命分布类与可靠性数学理论[M].北京：科学出版社，1999.

[5]市田，铃木和幸.可靠性分布与统计[M].北京：机械工业出版社，1988.

[6]胡昌寿田.可靠性工程设计实验分析管理[M].北京：宇航出版社，1989.

[7]叶中行，杜之韩，柳金甫，陈珊敏.概率论与数理统计[M].北京：科学出版社，2001.