基于HP滤波和GARCH模型的股票价格趋势预测
2013-07-27杨建辉张然欣
杨建辉,张然欣
(华南理工大学工商管理学院,广州 510000)
0 引言
在股票市场中,对市场状况最直接的反映就是各种股票的价格及其变动,并由此派生出其它各种表征市场状况的特征量。其中,股票价格是最基本的特征量,也是人们所能感觉到的最直接的表现,其它特征量则是以股票价格为基础的间接量。而关于股票的价格,它总是处在不停的波动变化之中,受政治、经济以及市场技术等多方面的因素的影响。目前已形成的各种股价理论虽然能解释股市上的某些现象,但对股票价格的描述和分析都不完全、不确切。
HP滤波方法是对非平稳变化的股票价格序列进行趋势分解,分解成为不同性质的数据序列。龚攀峰(2009)基于HP滤波由失业率和经济增长率得到潜在失业率和经济增长率,进而计算出失业率缺口和经济增长率缺口[1];张连城、韩蓓(2009)结合1952-2007年中国年度产出数据特征,讨论了应用HP滤波方法测算潜在产出时的平滑参数选择问题。平滑参数取100时的HP滤波器能更准确地刻画长期增长路径,平滑参数取6.25时的HP滤波器能更好地捕捉潜在产出的波动特点[2];彭兆祺、孙超(2011)采用HP滤波方法,对我国经济的长期均衡增长或潜在增速进行考察,分析了经济周期的变化,长期均衡经济增长显示出经济周期扁平化,波动幅度放缓更加明显,波谷、波峰的间距由5年延长到目前的6年和8年[3]。
GARCH模型主要运用于中国股票市场波动性的预测,但是国内GARCH模型用于金融产品价格趋势的研究不是很多,研究的比较多的是对人民币汇率的预测。刘国旗(2000)应用GARCH模型及其两种非线性修正模型(QGARCH模型和GJR模型)预测中国股票市场的波动[4];Brooks和Simon按照一定的标准选用特定的GARCH模型来预测美元汇率的收益波动情况[5];惠晓峰(2003)运用时间序列的GARCH模型,采用一步向前预测的滚动算法和递归算法,对汇率体制改革后的人民币美元汇率建模进行预测[6];罗艳(2011)用ARMA和GARCH模型预测沪深300消费指数的变化趋势进行了进行全局预测和短期预测[7]。
在综合比较国内外学者运用GARCH模型预测方法的基础上,本文选择采用HP滤波法与GARCH模型对股票价格的基本走势进行研究,希望通过这些方法的验证为股票价格走势的预测提供较为科学的依据,但是股票价格的决定因素是非常复杂的,本文将HP滤波法与GARCH模型结合起来对股票价格进行的分析预测只是一种尝试,更多的是一种思路和方法方面的探索。
1 模型思想及其方法
1.1 HP滤波模型的基本思想原理
HP滤波是在宏观经济分析用来的到经济时间序列的长期趋势而广泛使用的方法之一。它是由Hodrick和Prescott提出的一种滤波方法,即认为经济变量变动趋势是缓慢的,不是永远不变也不是随机波动而变,它把经济运行看作是长期内在的或者潜在的增长趋势和短期波动的结合,把实际产出分解为趋势和周期性两种成分[3]。该方法采用对称的数据移动平均的方法原理,设计了一个滤波器,将变化不定的时间序列数据中具有一定趋势变化的平滑序列分离出来。于是时间序列数据就被分为两部分:周期性波动数据和趋势要素数据。
对于时间序列数据S={s1,s2,…,sn}来说,假如分解出来的周期性数据为 Y={y1,y2,… ,yn},趋势要素为 T={t1,t2,… ,tn},则S=Y+T,i=1,2,…,n。
趋势被定义为下面的最小化问题的解:
式中的λ为正数,用以调节两者的比重,称为平滑参数,是控制平滑程度的惩罚因子。该值越大,则T越平滑,当该值趋向于无穷时,第二项为0。这时,HP滤波退化为最小二乘法。
HP滤波法也有自己的局限性,其一:HP滤波法的结果跟取值有很大的关系;其二:HP滤波法要求考察趋势值和实际值的缺口之和为0,从而尾点的数据会严重的影响结果。
1.2 GARCH模型的基本思想原理
金融市场价格波动具有随时间变化的特点,经济学家和金融财务专家们研究发现金融市场上时间序列数据从一个时期到另一个时期的变化过程中,常常出现价格波动率聚类现象。即大幅度波动聚集在某一段时间,而小幅度波动聚集在另一段时间上。这时称该时间序列存在条件异方差,建模就需要用到条件异方差模型[8]。
传统的回归模型在古典假设中要求扰动项具有同方差性,但是不能解释金融数据尖峰厚尾、波动丛集性和杠杆效应的特征。这种情况下,为了充分地描述金融资产收益率的波动特性,在原有的ARCH模型基础上Tim Bollerslev在1986年该模型中增加了q阶自回归项,称为推广的ARCH(GARCH)模型。GARCH是一种使用过去变化和过去方差来预测将来变化的时间序列建模方法。它的优势在于可有效的排除资产收益率中的过度峰值该推广的模型解决了原有模型固有的缺点,使待估参数大为减少并且提高了计算的准确性。
GARCH模型一般由两个方程组成:一个是条件均值方程,另一个是条件方差方程。这两个方程通常可以表示为:
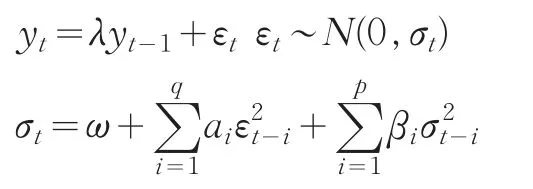
其中p≥0,q>0。当期的方差依赖于三个因素:常数项ω,ARCH 项(用前一期的残差的平方表示,反映前一期的波动性)和前一期的预测方差
1.3 基于HP滤波法的自回归和GARCH模型
令S={s1,s2,…,sn}为某段时间获得的股票时间序列数据,其为波动非平稳序列,首先对该序列进行HP滤波,运用Eviews[12]辅助工具将数据分解成具有时间规律变化的趋势数据和带有循环周期的随机波动序列,S=Y+T。
首先,对分解出来的趋势元素序列T采用自回归模型进行拟合和预测。根据可判系数最大和AIC、SC准则最小来确定模型的阶数,然后得到自回归模型。根据模型然后对趋势元素序列前400个数值进行拟合,然后对样本外的89个数据进行预测,得到预测的趋势元素序列Tf。给出自回归模型未预测的带有周期的随机波动序列Y0,且Y0=S-Tf。
然后,对序列Y0进行ARCH效应的检验,试利用GARCH模型对其进行前400个数值拟合,然后对样本外的89个数据进行预测,根据AIC、SC准则最小来确定模型的阶数并确定模型的系数,最后给出GARCH模型预测的Yf。
最后,通过对数据进行重组,得到原始序列S样本外89个数据的预测序列Sf=Y0f+Tf,并根据原始时间序列数据和预测序列数据的趋势图进行比较来分析模型的预测效果。
2 实证分析
2.1 数据额选取
本文选取了中国股市中具有代表性的股票上证指数,选取的是2010年1月4日到2011年12月30日的日收盘价数据共489条。样本容量大使得模型的拟合效果更好,得出的结论也更具说服力。选取前400个数据进行模型的建立,然后对样本外的89个数据进行样本外预测。本文的数据处理与分析选用的软件是Eviews5.0和ExceL2007。数据分析
2.2.1HP滤波对数据的分解
在HP滤波中,取λ=100。将原始时间序列数据分解成趋势项序列和周期项序列,得到的分解结果如下图1所示。

图1 HP滤波分解图
从图1中可以看出,HP滤波分解出具有较平滑趋势的红色曲线数据Trend和具有波动规律的绿色曲线数据Cycle,红色曲线数据即为趋势要素序列T,绿色曲线数据为周期性序列数据Y。然后,分别用自回归模型和GARCH模型对分解出的数据进行拟合和预测。
2.2.2 自回归模型的拟合和预测
运用自回归模型对趋势要素序列T进行模拟和预测。通过可判系数最大和AIC、SC准则最小原则来确定模型的阶数,经过多次拟合确定为4阶,其R-squared=0.9999,因此其拟合效果是很好的。
自回归模型中参数为:
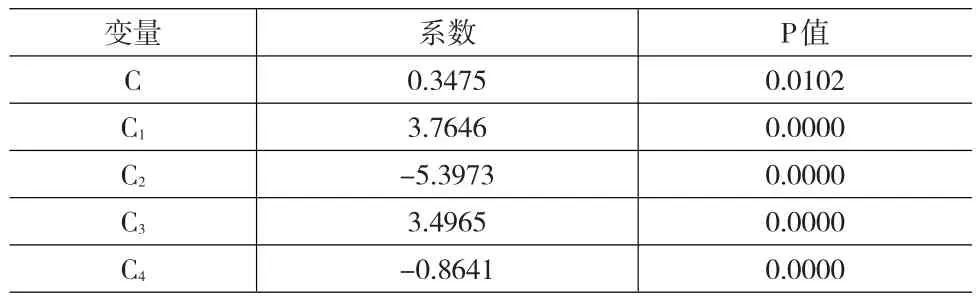
表1 模型参数
因此模型的表达式为:
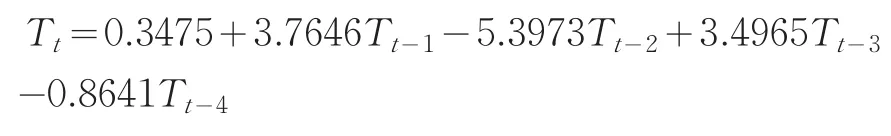
在模型的基础上采用静态预测法对样本外的89个数据进行预测,预测效果如图2所示:
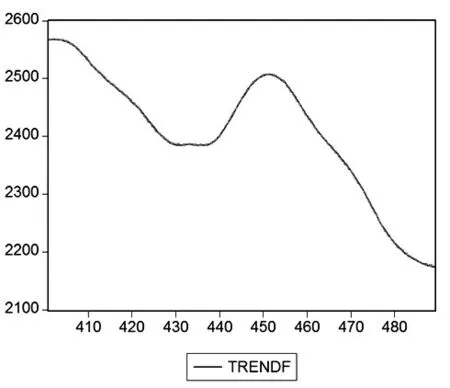
图2 趋势元素样本外预测
如图2所示,其中红色曲线为部分原始趋势序列T,蓝色曲线为部分趋势元素预测序列Tf,由此得到自回归模型未预测的带有周期的随机波动序列Y0=S-Tf,然后利用GARCH模型对Y0进行拟合和预测。
2.2.3 GARCH模型的拟合和预测
(1)基本描述统计量。

表2 基本描述统计量
由表2可知,股票的周期性序列表现出负偏度,因而拒绝原序列服从均值为0的正态分布的原假设;同时表现出很高的过度峰度(峰度>3时成为过度峰度),Jarque-Bera正态检验检验量也拒绝正态分布的原假设,股票周期性序列存在明显的波动聚集和尖峰、厚尾现象,传统的基于正态分布假设的静态模型不足以捕捉序列的这一特性。因此,我们选择基于GARCH模型来对其进行拟合。
(2)平稳性检验。
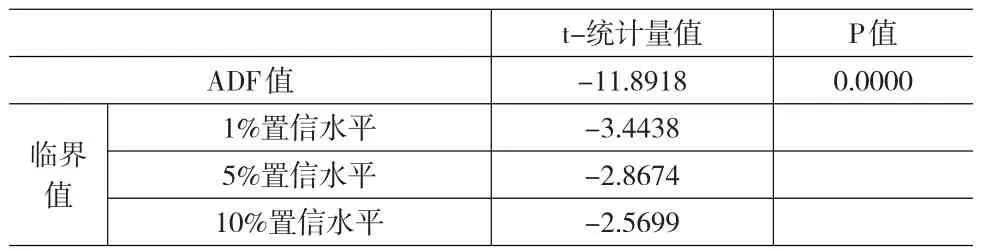
表3 周期性序列的ADF检验
表3中,P=0.0000,拒绝原假设,即周期性序列不存在一个单位根,即认为周期性序列是平稳的。下面对周期性序列的自相关性进行检验。
(3)周期性序列的自相关性检验。
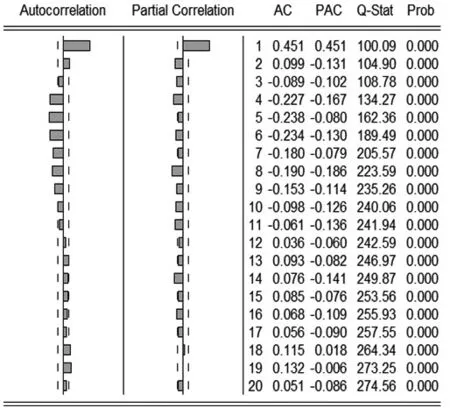
图3 周期性序列的自相关性检验
如图3所示,根据周期性序列Y0的自相关函数(ACF)和偏自相关函数(PACF)值以及P统计量的值可知,Y0存在着明显的自相关性。
周期性序列Y0为平稳序列但是存在自相关,所以方程为均值回归方程。因此我们可以把Y0的生成过程设为如下均值方程的形式:
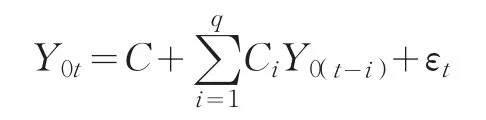
因此我们需要根据AIC、SC准则最小原则进行多次尝试来确定模型的阶数q值。
(4)异方差性检验。
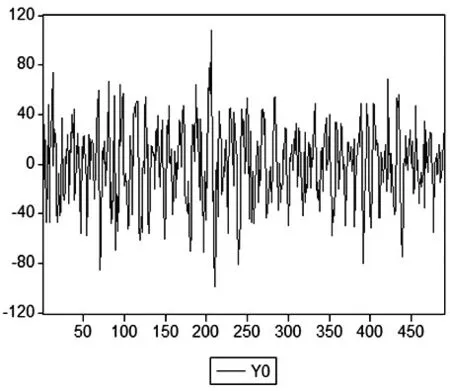
图4 周期性序列Y0的直线图
通过图4对周期性序列Y0的直线图进行观察可以看出,Y0存在着明显的“集群效应”,即一次大的波动后面伴随着大的波动,一次小的波动后面伴随着小的波动,即认为序列Y0存在着异方差。
(5)GARCH模型的拟合与预测。
通过上边的分析我们知道周期性序列Y0存在着自相关性,均值方程如式(1)所示的形式,通过采用EVIEWS5.0软件根据AIC、SC准则最小原则我们确定建立了立起AR(2)-GARCH(1,1)模型。结果如下:

(6)ARCH LM效应检验。

表4 ARCH LM效应检验
该检验用来分析标准残差是否存在着额外的ARCH效应。表4计算结果表明,对1阶滞后、10阶滞后、20阶滞后的残差进行估计,F统计量和Obs*R2统计量均不显著,表明标准残差不存在额外的ARCH效应,同时也再次表明方差方程的估计是准确的[6]。
在模型的基础上我们对Y0进行拟合,在前400样本的基础上利用静态预测法对其余的89个数值进行样本外预测得到序列Y0f。
2.3 预测效果分析
将自回归模型预测的趋势元素序列Tf和GARCH模型预测到的数据Y0f进行重组,得到原始序列S样本外89个数据的预测序列Sf=Y0f+Tf,现将样本外预测的89个数据的预测序列与原始序列的比较如下图5所示。

图5 原始值与预测值趋势图
在图5中,蓝色曲线是原始的股票时间序列数据S的89个样本序列,红色曲线SF是89个数据的预测序列。从图中我们可以看出,该模型的预测效果,预测值的趋势与原始数值的趋势趋于相同,因此我们认为该模型对于股票价格趋势的预测能够提供帮助。
3 结论
由于影响股票价格的因素是及其复杂,因此很难建立一个很精确地模型对股票价格进行预测。本文中通过HP滤波法将复杂多变的股票数据进行分解,分解为趋势元素数据和具有波动性的序列数据,对不同性质的数据并分别采用自回归和GARCH模型对数据进行拟合回归,在拟合较好的基础上对上证指数股票的价格趋势进行预测。实例结果表明,预测数据的趋势与原始数据区域相同,因此基于HP滤波的GARCH模型对于预测股票价格的趋势效果很好,在实际中应用具有一定的参考价值。本文对股票价格趋势进行的分析预测只是一种尝试,更多的是一种思路和方法方面的探索,希望可为金融产品的趋势研究提供帮助。
[1]龚攀峰.基于HP滤波失业率失衡和经济增长失衡的内在机制分析[J].统计教育,2009,(10).
[2]张连城,韩蓓.中国潜在经济增长率分析[J].经济与管理研究,2009,(3).
[3]彭兆祺,孙超.基于HP滤波分析方法的我国经济增长研究[J].山西财经大学学报,2011,33(1).
[4]刘国旗.非线性GARCH模型在中国股市波动预测中的应用研究[J].统计研究,2000,(1).
[5]Chris Brooks,Simon P.B.Forecasting Exchange Rate Volatility Using Conditional Variance Models Selected by Information Criteria[J].Eco⁃nomics Letters,1998,(61).
[6]惠晓峰等.基于时间序列GARCH模型的人民币汇率预测[J].金融研究,2003,(5).
[7]罗艳.用GARCH模型预测沪深300消费指数的变化趋势[J].科技向导,2011,(15).
[8]陈志民,陈恩爱,杨乃如.非线性GARCH模型在人民币汇率预测中的应用[J].宜春学院学报(自然科学),2007,29(2).
[9]张晓峒.Eviews使用指南与案例[M].北京:机械工业出版社,2007.
