我国批发零售业宏观营销效率因子分析
2013-07-27谢江波
刘 苏,万 涛,谢江波,毛 羽
(1.华中科技大学公共管理学院,武汉 430070;2.湖北省科技信息研究院,武汉 430071;3.中广传播集团有限公司,北京 100000)
对宏观营销效率的分析可从分销部门营销效率和物流业营销效率这两个层面来衡量。但是截止目前,有关这两个层面的系统研究不多,而且已有研究多倾向于使用定性方法,较少涉及定量分析。同时多从全国总体效率进行分析,没有涉及各地区宏观营销效率分布情况。因此,本文拟采用定量的方法,对作为宏观营销效率重要组成部分的各地区批发零售业宏观营销效率进行系统研究,以期得出更为客观的结论。
1 批发零售业宏观营销效率指标体系构建
Engle(1941)认为,营销效率的分析应包含批零企业数量、销售净额、经营费用、每一美元投入(表现为经营费用)所获得的产出(表现为销售净额)、从业人员数量、每一从业人员平均销售额等指标。Turck(1948)在Engle的基础上提出,应将人·时生产率也纳入营销效率的考察范围。Moyer(1972)进一步提出了衡量分销系统效率的4个指标:商品销售总额中分销费用所占比重、总就业人员中流通领域就业人员所占比重、零售商品总额中毛利所占比例、流通领域人·时产出年均增长率同生产部门人·时产出年均增长率相比较。综上所述,营销效率的衡量紧紧围绕投入和产出两方面。本文在数据可获得的前提下,重点选取了能反映投入产出对比关系和批零企业增长情况的12项指标来构建指标体系,从而在一定程度上来反映批零企业的盈利效率、管理效率、成长效率和规模效率。选用的指标体系见表1:
其中平均每个商店雇佣的人员数是逆指标,指标值越大,营销效率越低;其它指标都是正指标。
2 数据来源与计量方法
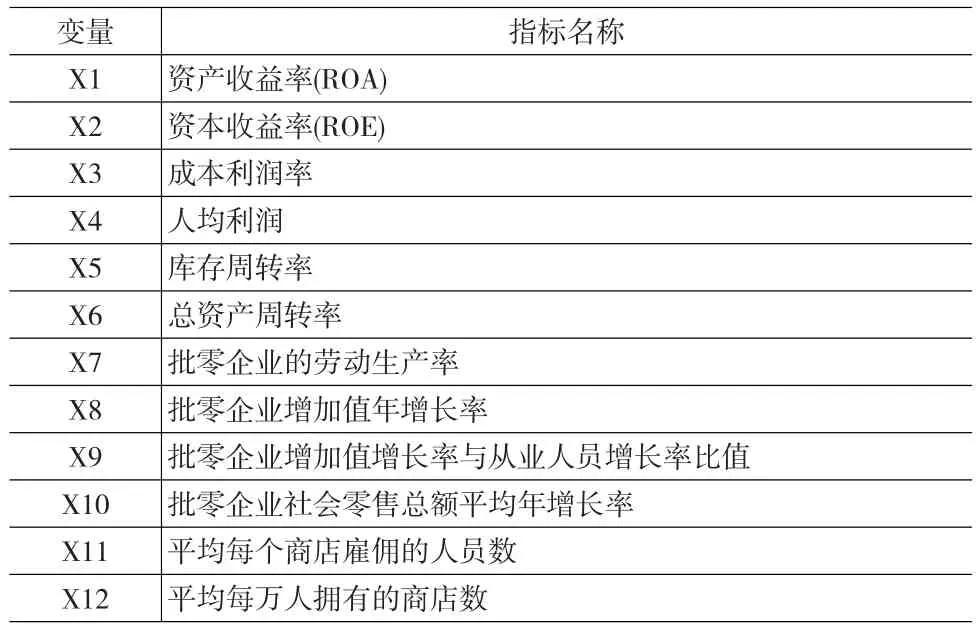
表1 批发零售业宏观营销效率指标体系
2.1 数据来源
本文收集了全国31个省、自治区、直辖市的相关数据,数据全部来自统计年鉴。变量X1、X2、X3、X4、X5、X6、X7、X11和X12的数值根据2011年《中国统计年鉴》横截面资料计算求得。变量X8、X9和X10的数值根据1997-2011年《中国统计年鉴》纵向资料计算求得。其中国家在1998年将重庆市改为直辖市后,我们将重庆市和四川省的资料按统一口径进行了调整。各省指标具体数值见表2。
2.2 计量方法
基于各项指标数据量纲不一致,故先对这些指标进行综合集成和无量纲化处理。主要原理如下:
设X=(X(1),…,X(p))为P维随机变量,∑为X的协方差阵,即:
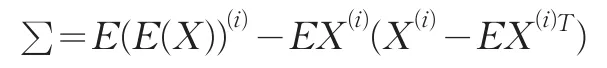
因为X的协方差阵∑是非负定的,由对称阵的性质可知,必存在正交阵U(Uτ=U-1)使
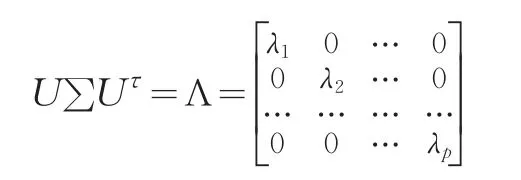
对角阵Λ的对角线元素λ满足λ1≥λ2≥…≥λp≥0,以Uj表示UT的第j列,即UT=(U1,U2,…,Up),ZΔ=UX=(U1,U2,…,Up)TX,则Z的诸分量Z(j)=UTX,此时Z的协方差阵为δ。
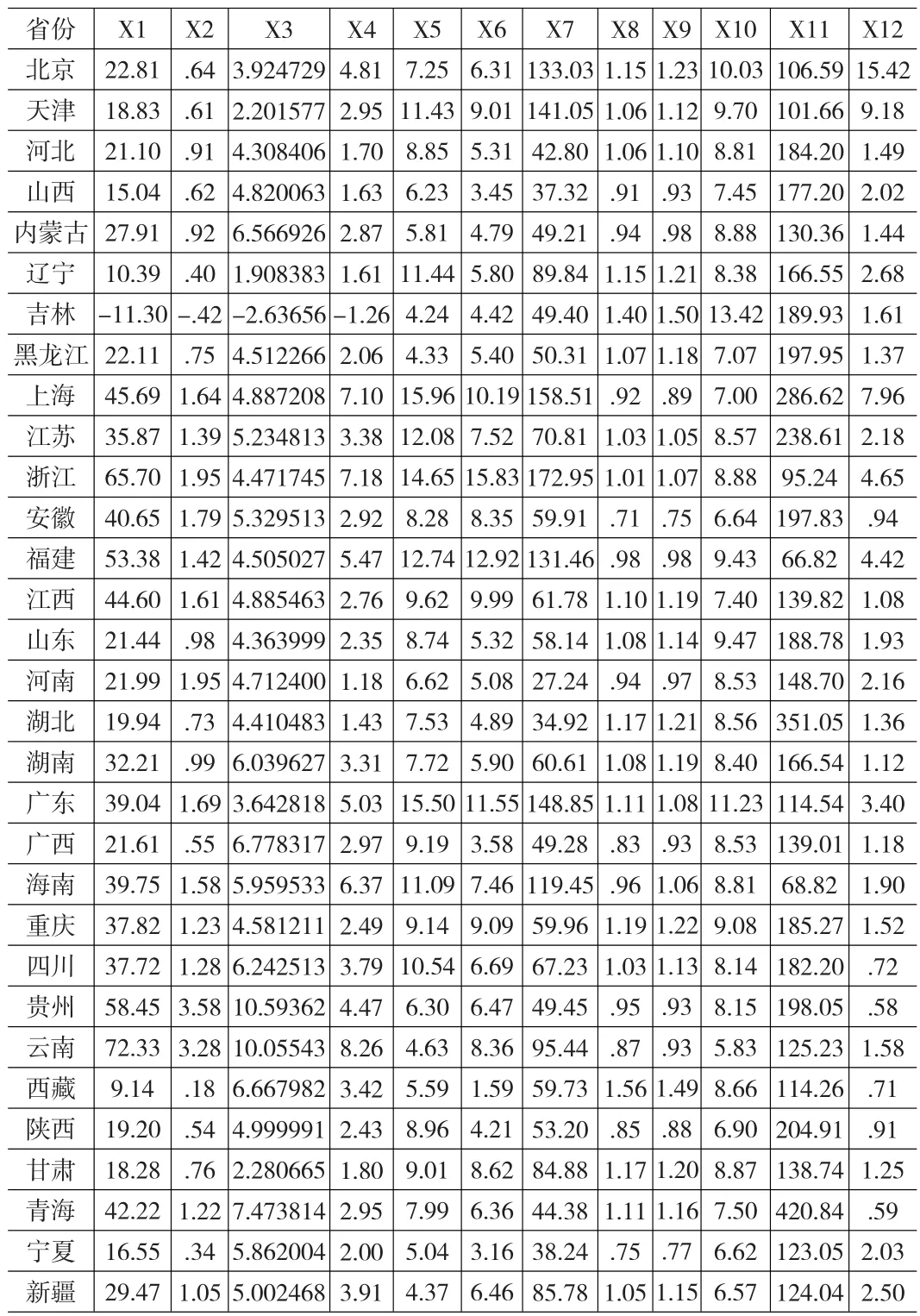
表2 各地区批发零售业宏观营销效率指标值(全国31个省市自治区资料)
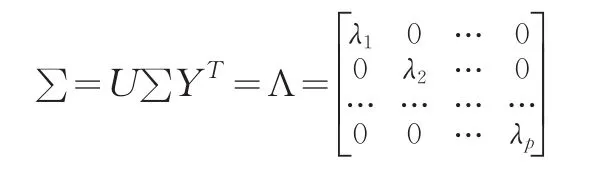
Z有如下性质:
性质1:Z(1),Z(2),…,Z(p)是互不相关的向量,且λj是Z(j)的方差。
性质2:若B为任一p维向量,BTB=1,则maxD(BτX)=λ1,且当B=U1时,D(U1xx)=D(Z(1)=λ1)。
性质3:若B为任一p维向量,与U1,U2,…,Uj-1正交,且BτB=1,则:
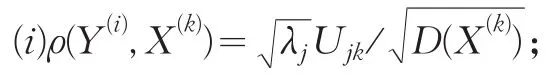
性质4:设U=(Ujk),则Z(j)与X(k)间的相关系数
(ii)
(iii)为X的第j个主成分,称为主成分Z(j)的贡献率称为Z(1),Z(2),…的累积贡献率,p(Z(j),Z(k))称为因子负荷量。以上性质说明,经过正交交换处理,Z各分量之间互不相关,其主成分是一定条件下解释X这个随机变量差异能力最强的线性组合。
通常,协方差阵或相关系数矩阵的特征值之间差异很大,因而通过指定的贡献率来确定的主成分个数小于原来分量个数。由此可见,在不损失原有信息的条件下,主成分分析法可以显著的压缩随机变量的个数。
Z各分量之间互不相关,当X服从多元正态分布时相互独立,各主成分分析法可以用来有效剔除观测资料中的冗余信息。并且,各分量之间互不相关的性质也便于将子系统的数学模型经过调整集成后获得大系统的数字模型。
2.3 构造宏观营销效率指数基本程序
在SPSS软件环境下编制主成分分析法程序,以标准化了的地区宏观营销效率数据作为输入,计算出地区宏观营销效率表现要素的相关矩阵,然后进一步通过相关矩阵求得特征值、累计特征值及主成分的载荷。再根据最初的几个特征值在全部特征值的累计百分率大于或等于百分率的原则决定选取主成分的具体数值。假定前m个主成分分别为:
Zi1=fi1(xi1,xi2,…)
Zi2=fi2(xi1,xi2,…)
Zi3=fi3(xi1,xi2,…)
Zim=fim(xi1,xi2,…)
将第Ⅰ地区各解释变量的数值标准化后代入,可求得Z1、Z2、…、Zm的数值,然后将这m个主成分对应的特征值加权累加,从而构造一个地区的宏观营销效率,其数学表达式如下:
E1=[λimZi1+λi2h+…+λimZim],其中Ei为宏观营销效率指标,λi1,…,λ1m为前m个特征值。基于上面的计算数据,可进行一定的实证分析。通过主成分分析构建的宏观营销效率会出现一部分负值。需要说明的是,这里的负值仅仅代表宏观营销效率的相对水平,即表明该地区在所有被考虑选地区中的相对地位是低于平均水平的。
3 我国各地区宏观营销效率分析
3.1 求R特征值与贡献率
使用SPSS11.5统计分析软件,处理表2中的数据。首先将各项评价指标的原始数据标准化,然后建立变量的相关系数矩阵R的特征值及贡献率。发现变量的相关系数矩阵有四大特征根:3.180、3.077、2.429、1.477,它们对宏观营销效率指标标准差的累计贡献率为84.695%。这意味着前四个成分显示了原始数据所提供的足够信息。同时,过程内特征值均大于1,四个特征值全部符合要求(最小特征值为1.477),主因子分析过程相应提取四个主成分量:F1、F2、F3、F4。
3.2 构建因子载荷矩阵
首先,我们为四个主因子分量F1、F2、F3、F4建立原始因子载荷矩阵,然后对其结构进行调整和简化,最终得出方差最大正交旋转矩阵,这也就是标准化后前四个主成分的载荷矩阵。同时,根据正交载荷阵中高载荷,将指标值分为四类,可以看出第一个主因子在X1、X2、X3、X 4上有较大载荷,其中X1和X2是衡量宏观营销盈利效率的核心指标,X3是较为全面反映各地批发零售业宏观营销的获利效率的指标,X4是从人力资源角度反映宏观营销收益潜力的指标。这4项指标都可以从某个方面反映批发零售业盈利效率,因此我们称它们为获利效率因子。第二个主因子在X5、X6、X7上有较大的载荷,其中X5、X6综合反映企业的资产管理状况,不仅影响企业的偿债能力,也是整个企业管理的重要内容;X7反映企业人力资源的技术以及管理现状。可见X5、X6、X7是对货币资本、人力资本管理效率的反映,我们称之为管理效率因子。第三个主因子在X8,X9,X10上有较大的载荷,它们是各地批发零售业增长情况的综合反映,我们称之为成长效率因子。在第四个主成分上有较大载荷的是X11、X 12,它们分别反映批发零售企业的规模大小以及分布密度,我们称之为规模效率因子。以上四个主成分因子数值越大,则说明该地区的批发零售业宏观营销效率越高。
3.3 因子评分
因子评分以各因子的信息贡献率作为加重权数计算各地区批发零售业宏观营销效率的综合测评得分,公式如下:
Zi=0.312864F1i+0.302733F2i+0.239034F3i+0.145369F4i
其中,Zi为各地区批发零售业宏观营销效率得分,Fji的系数为各因子的信息贡献率,它是各因子的方差贡献率与四个主成分的累计贡献率的比值,则F1i、F2i、F3i、F4i的系数分别为0.312864、0.302733、0.239034、0.145369。通过计算最后得分得出各地区批发零售业宏观营销效率状况的因子综合测评分及排序,如表3所示。
从表6可以看出,浙江、广东、云南、福建、海南和北京批发零售业宏观营销效率最高,名列全国31个省、直辖市、自治区中的前6位;河南、安徽、广西、陕西、山西、宁夏的批发零售业宏观营销效率最低,名列后6位。排在前6位的省市除云南省不是沿海地区外,其他各省市基本上都属于沿海城市或我国的政治文化中心;而排在最后6位的省市,除广西外其他都属内陆省份或边远省份。
再从各项因子上进行分析。云南省作为一个经济并不太发达的省份之所以能在批发零售业宏观营销效率排名中进入前3名,主要得益于获利效率因子和规模效率因子,但是比较而言,其管理效率因子和成长效率因子仍得分较低,与全国先进省份相比仍有差距。而北京、上海作为全国的文化和经济中心,在此次总体排名中并不是太理想。
4 结论
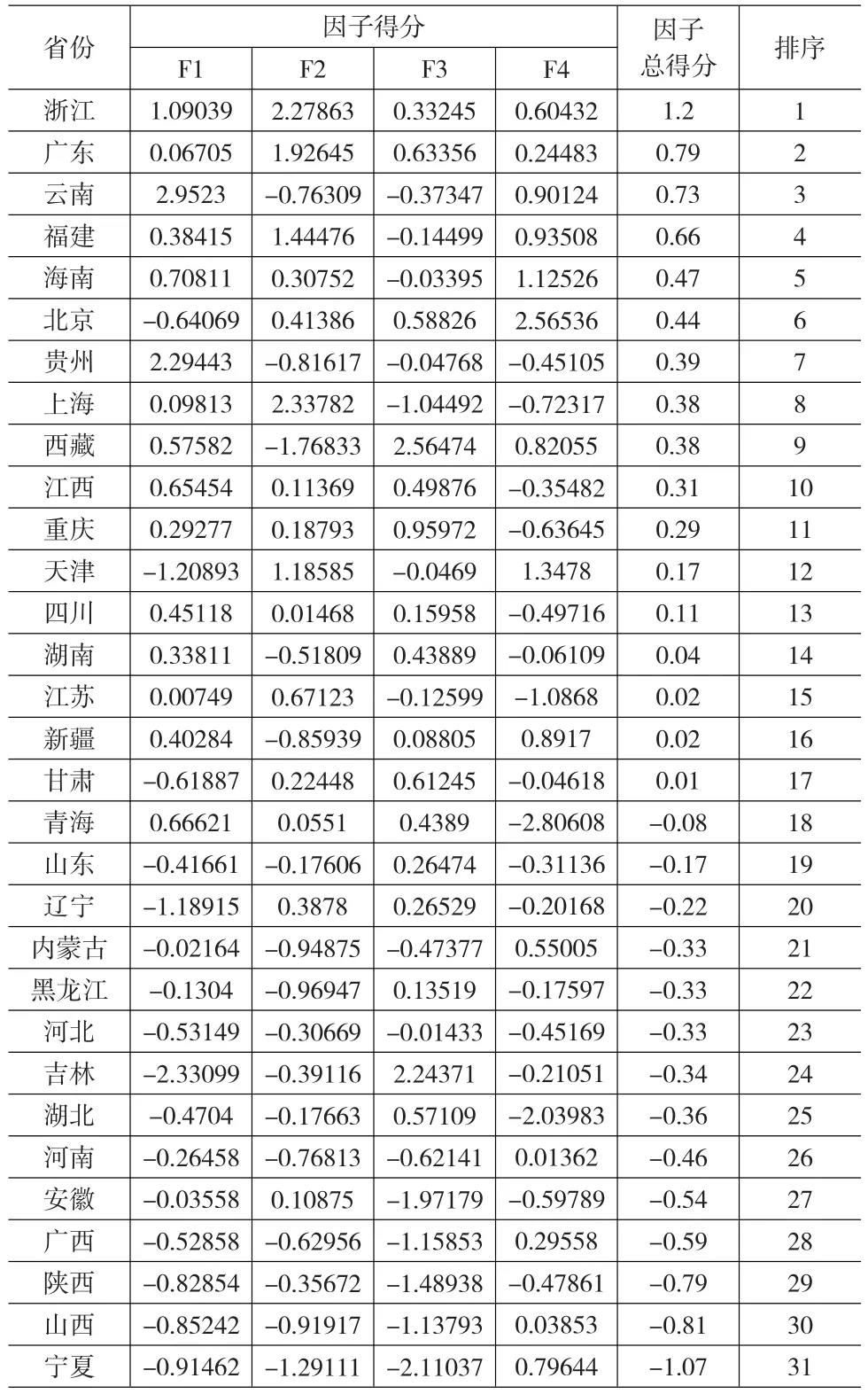
表3 各省直辖市自治区宏观营销效率评分及排序
综合各项因子分析结果,可以看出我国批发零售业宏观营销效率的高低走势并非与各地区的经济发展水平完全一致,但是能大体上反映一个地区的市场外向度,市场外向度高的地区的宏观营销效率相对较高。市场外向度主要通过地区的地理位置优势和政治文化中心来体现。
同时,全国各地区批发零售业宏观营销效率差异很大,效率高的只集中在少数几个地区,近一半地区的宏观营销效率在全国平均水平以下。这反映出我国批发零售业区域发展不平衡,同时在整体上仍处于较低水平,批发零售业的宏观营销效率和竞争力亟待提高。
[1]甘碧群,张雪兰.我国宏观营销效率分析[J].中国流通经济,2003,(9).
[2]甘碧群,王文超.批发零售行业的宏观营销效率研究[J].武汉大学学报(社科版),2003,(3).
[3]国家统计局.中国统计年鉴[Z].北京:中国统计出版社,1997~2011.
[4]李涛.我国35个大中城市人力资本投资实证分析[J].中国管理科学,2004,(8).
