基于DFIG自身无功能力提高风电场的电压稳定性的研究

2013-07-25高瑶陆浩李权周

电气开关 2013年2期

高瑶，陆浩，李权周

（1.河南省电力公司焦作供电公司，河南焦作 454150；2.四川同济京奥城市规划设计研究有限公司，四川成都 610051）

1 引言

作为一个间歇性、多变化的电源，大型的风电开发势必会面临如何顺利接入电网的挑战。随着并网风机规模的扩大，大规模风电出力变化将对电网造成很大冲击，加之地区电网网架不够坚强、电源结构较为单一，造成电网无功控制电压调节难度加大，给电网运行控制带来较多问题［1］。

风力发电具有随机性、间歇性、不确定性等特点，大规模的风电并网将会对电网稳定产生不利影响，其中电压无功控制调节问题日益突出，系统对风电场无功补偿设备的要求越来越高。

目前抑制电压的波动与闪变主要是在风电场出口处加装无功补偿装置，最常用的方法是安装静止无功补偿装置（SVC）或静止同步补偿器（STATCOM）。然而前者本身会产生低次的谐波电流，因此需要与滤波器并联使用；后者每单位容量的价格高昂，提升了风电场的投入成本，大型风电场广泛使用十分不经济。如何经济有效地适应风电出力的快速变化，并满足系统无功电压的控制需求，成为当今风电并网的一个重大课题。

目前我国的各大风电场中，双馈异步风力发电机（DFIG）得到了最为广泛的应用［2，3］，而有研究表明，多次脱网事故均与DFIG构成的风电场有关［4，5］，因此对DFIG进行深入研究，探讨其有效的电压无功控制策略将显得尤为重要。

本文主要针对双馈异步风力发电机有功、无功解耦控制的性能，建立了DFIG风力发电机模型，仿真分析了利用风机本身无功输出能力改善风电场暂态稳定性，探讨充分挖掘DFIG自身无功能力的可能性。

2 双馈异步风力发电机模型

双馈异步发电机的结构如图1所示，主要分为风力机、发电机以及换流器三个部分。

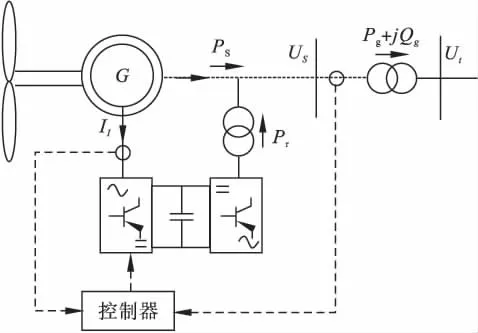
图1 双馈异步发电机结构图

2.1 风力机模型［6，7］

由空气动力学知识，风力机的输入功率为:

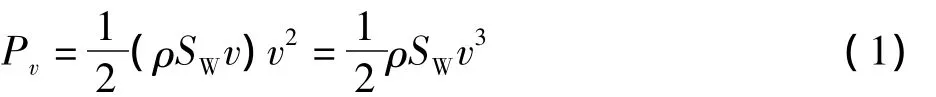
其中:ρ—空气密度；

SW—风力机的叶片扫风面积；

v—未扰动风速。

为叶尖速比，即叶片尖端线速度与风速的比值。其中w为风力机叶片的旋转角速度，R为叶片半径。

为风能利用系数，用来表征风力机捕获风能的能力。它与风轮直径、桨距角、叶片转速、风速等因素有关。CP是桨距角β与叶尖速比λ的综合函数:CP（β，λ）。一般在额定风速以下，桨距角基本处于零度附近，此时风能利用系数CP只是尖速比λ的函数。

则有风力机输出机械功率:

2.2 双馈电机模型［8－10］

假设电机定子、转子三相绕组对称且不考虑零轴分量，可得到同步转速ω旋转dq坐标系中的双馈电机数学模型。

电压方程:

磁链方程:

其中Ls为dq坐标系中定子等效两相绕组的自感；Lr为dq坐标系中转子等效两相绕组的自感；Lm为dq坐标系中定子、转子同轴等效绕组间的互感。

转矩方程:

其中Te为发电机的电磁转矩，np为电机的极对数。

运动方程:

其中TL为风力机发出的驱动转矩；J为风电机组的转动惯量。

2.3 换流器模型

2.3.1 网侧PWM变换器数学模型［11－12］

同步速ω旋转dq坐标系下，网侧PWM变换器数学模型为:

其中，ugd、ugq分别为网侧电压的d、q轴分量；igd、igq分别为输入电流的d、q轴分量；vgd、vgq分别为换流器交流侧电压的d、q轴分量；sd、sq分别为开关函数的d、q轴分量。

2.3.2 转子侧PWM变换器数学模型［2，13］

为了实现对双馈电机的有功功率、无功功率的有效控制，需采用矢量控制技术，通过坐标变换将转子电流有功分量、无功分量进行解耦，并对两个分量分别控制，在变速恒频条件下实现最大风能追踪，得到当前风速条件下最大功率输出；实现无功功率的有效控制，保证电网稳定。同步速ω旋转dq坐标系下，d轴定向于电网电压矢量，转子侧PWM变换器数学模型为:

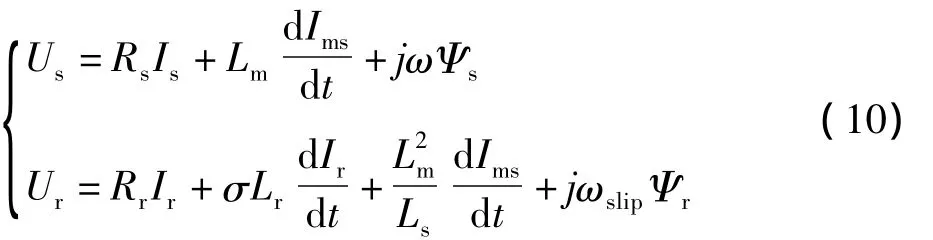
其中，Us、Ur分别为电机定子、转子电压矢量；Is、Ir分别为电机定子、转子电流矢量；Ψs、Ψr分别为电机定子、转子磁链矢量；Ims为定子的等效励磁电流矢量；σ为发电机的漏磁系数。

3 暂态电压控制模型

通过DFIG的转子侧变频器控制，在电网发生故障导致电压波动时发出无功功率参与暂态电压控制，抑制参考点电压波动，并能在故障后恢复正常值。本文将DFIG机端电压作为参考点，暂态电压控制框图如图2所示。

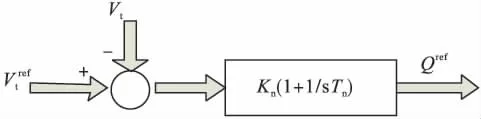
图2 暂态电压控制框图

4 仿真算例

4.1 仿真模型

本文采用的算例为由多个风机等值的一台风机通过变压器和线路连接到系统母线。接线如图3所示。

图3 仿真系统连接图

本文采用的算例为由多个风机等值的一台风机通过变压器和线路连接到系统母线。接线如图3所示。

风力机采用“1+1”等值模型［15］，由 6 台 2.2MW双馈异步风电机组等值成为一台13.2MW风电机。等值后风机的参数如图4所示。

出口电压为690V，经升压变压器升至10kV，通过输电线路连接到大系统。仿真中风速保持额定风速10m/s。

4.2 仿真算例

仿真一:风电场侧10kV线路在t=1s时发生单相接地故障，故障持续时间为0.08s，10kV母线B2电压Vabc、风力机机端电压Vt、换流器电容电压Vdc如图4、图5、图6所示。

图4 故障后10kV母线B2电压Vabc（V）

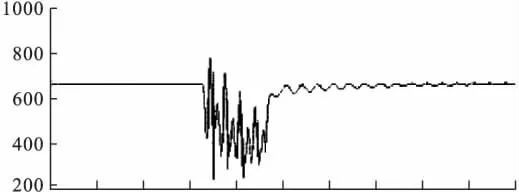
图5 故障后风力机机端电压Vt（V）

图6 故障后换流器电容电压Vdc（V）

仿真二:风电场侧10kV线路在t=1s时发生单相接地故障，故障持续时间为0.08s，控制风机对应故障持续发出无功约1MW，10kV母线B2电压Vabc、风力机机端电压Vt、换流器电容电压Vdc如图7、图8、图9所示。

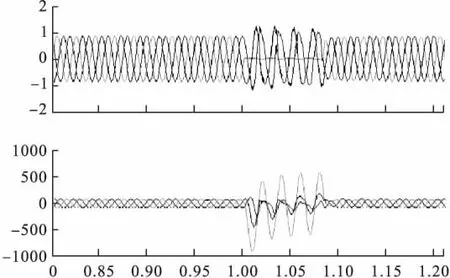
图7 风机无功支持后10kV母线B2电压Vabc（V）

图8 风机无功支持后风力机机端电压Vt（V）

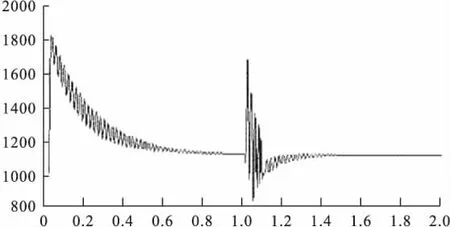
图9 风机无功支持后换流器电容电压Vdc（V）

4.3 仿真分析

（1）由图4、图7对比得知，故障后10kV母线B2电压Vabc有波动，在故障切除以后恢复正常，说明风机在经受单相接地故障后可以维持稳定运行不至失稳。

（2）由图5、图8对比，图6与图9对比可以看出，故障时风机机端电压出现震荡，在风机加入无功支持以后，电压震荡幅度有所减小，机端电压震荡得到抑制；故障时换流器直流侧电压Vdc出现震荡，在风机加入无功支持以后，电压震荡幅度有所减小，机端电压震荡得到抑制。说明了风机自身的无功能力可以改善风机自身的电压失稳现象，使得风机运行更加稳定。