电力系统安全与稳定运行问题分析
2013-07-25莫衍毅
莫衍毅
(广西电网公司横县供电公司,广西 横县 530003)
1 引言
目前的中国电力市场化改革不断深入,电力市场的运行前提是必须保证电网安全、稳定运行,电力市场化改革决不能以牺牲电力系统的安全和可靠性为代价,电力体制改革成功与否的重要标志是电网运行的安全性与稳定性[1-4],电力市场化进程是电力工业发展的必然趋势,安全性与稳定性是电力系统运行中最重要的因素[5-9]。
2 电力系统的安全运行条件
随着现代通信技术和信息技术的发展,为了保障大电网的安全和经济运行,各种信息系统在电力系统领域里得到了广泛应用,图1为现代电力系统整体框架。

图1 现代电力系统整体框架
电力系统的运行条件可描述如下:
功率平衡约束方程,即等式约束条件,包括系统的有功功率和无功功率平衡:

式中:PGi、QGi—电源的有功与无功功率;
PLj、QLj—负荷的有功与无功功率;
ΔPs、ΔQs—有功与无功的总损耗。
运行约束条件,即不等式约束条件,包括节点电压约束、发电机有功约束和无功约束、线路潮流约束为:




2 电力系统的静态电压安全裕度
电压安全准则基于电压安全裕度,一般是指系统需要保持多少的电压安全裕度才认为其电压安全裕度是符合电压安全准则的。
计算电压安全裕度是进行电压安全评估的一个重要步骤,即电压当前运行点到崩溃点之间的距离,关键是如何确定电压崩溃点,计算崩溃点的方法有很多种,概括起来可以分为以下几类。
(1)崩溃点法
崩溃点法的数学模型为:

式中:f—潮流方程组成的方程组向量;
x=[δ,V]T—系统状态变量;
μ—负荷参数;
re、le—右、左特征值向量。
崩溃点法的理论基础是分歧理论和雅可比矩阵奇异理论,是通过直接求解系统在电压崩溃点所满足的非线性方程组获得电压崩溃点的值。
(2)最小奇异值法
矩阵的最小奇异值分解公式为:

式中:A∈Rm×m;
U、A—m×m正交矩阵;
ui、vi—U、V的左右奇异向量;
B—对角矩阵。
则当负荷和发电机节点的注入功率改变时δmin变化量的近似表达式为:

式中:J—雅可比矩阵。
常规潮流雅可比矩阵的奇异度与电压稳定之间有着密切关系,用潮流雅可比矩阵的最小奇异值作为定量衡量系统运行点与电压崩溃点临近程度的指标。
(3)最优潮流法
潮流方程和雅可比矩阵奇异为约束条件的最优化模型为:

条件如下:

式中:wT—拉格朗日乘子向量。
最优潮流法是直接法的一种,直接计算运行点到崩溃点之间的负荷增量,不要求基础运行情况到极限点的解轨线。
3 电力系统安全经济调度模型
以发电成本最小为目的的电力系统安全经济调度模型:
目标函数为:

式中:NG—系统中的机组台数;
T—优化时段数;F()—机组i的发电成本函数;
—机组i在时段t的出力。
约束条件为:
(1)系统功率平衡约束

式中:T—调度周期的时段数;
—时段t的负荷量。
(2)线路有功功率传输限制约束

其中:l=1,…,L;t=1,…,T。
式中:—线路l在时段t的有功功率;
Pfl.max、Pfl.max—线路l有功的上、下限。
(3)机组出力约束

式中:PGi.min、PGi.max—机组出力上、下限。
(4)机组爬坡速率约束

式中:—优化前一时段的机组出力;
UGi、DGi—机组上、下爬坡速率限制。
处理线路有功功率传输限制时,当采用直流潮流方程作为约束条件时,一般采用节点功率转移因子将线路有功功率表示为节点注入功率的线性函数。直流潮流计算方法如下:

式中:Sfl-k—节点k对线路l的转移因子;
Pfij—直流潮流中线路有功功率;
θi、θj—节点i、j的电压相角;
xij—线路ij的电抗。由于:

则:

节点功率转移矩阵可表示为:
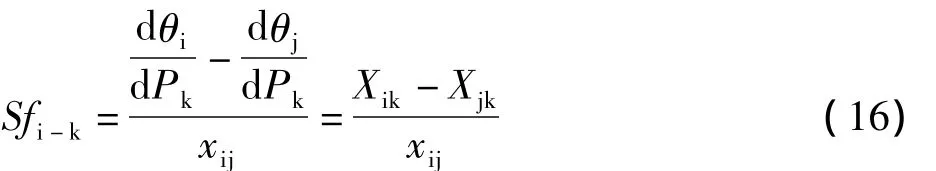
在已确定的电力系统中,线路阻抗参数固定,系统的节点功率转移因子为常数,则有功功率可表示为节点注入功率的线性函数:

4 电力系统的暂态失稳概率
一般认为电力系统中发生故障的概率基本服从泊松分布,其表达式为:

式中:P(Ei)—线路发生故障的概率;
λi—线路i的故障率。
故障类型的概率为:

式中:fi—第i种历史故障发生的次数;
M—4,表示四种常见故障。
故障清除时间的两种表达形式为:

重合闸失败的概率公式为:

式中:Pr—重合闸失败的概率;
P(L)、P(O)—雷击和其他原因引起的故障概率;
P(U|L)、P(U|O)—雷击和其他原因引起的重合闸失败概率。
5 总结
目前,随着电力系统规模的不断扩大以及电力市场化改革的深入,电网的安全稳定问题受到越来越多的关注和重视,对电力市场环境下的电网安全性与稳定性的研究十分必要和迫切。我国的电力工业的市场化改革刚刚起步,电力市场会对电网的安全性与稳定性造成何种影响,以及在市场环境下如何更好地提高电网的安全性与稳定性,这些都是必须认真考虑的问题。
[1]余贻鑫,陈礼义.电力系统的安全性和稳定性[M].北京:科学出版社,1988.
[2]袁季修.电力系统安全稳定控制[M].北京:中国电力出版社,1996.
[3]袁季修.电力系统安全稳定控制的规划和应用[J].中国电力.1999,32(5):29 -32.
[4]孙元章,杨新林,王海风.考虑暂态稳定性约束的最优潮流问题[J].电力系统自动化,2005,29(16):56 -59,53.
[5]夏清,彭涛,江健健.兼顾经济协调发展和电网安全的区域共同市场[J].电力系统自动化,2004,28(19):1 -5.
[6]谭伦农,张保会,刘海涛.市场环境下电力系统的安全可靠性问题[J].电力系统自动化,2002,26(6):11 -14.
[7]余贻鑫,赵义术,刘辉,等.基于实用动态安全域的电力系统安全成本优化[J].中国电机工程学报,2004,24(6):13 -18.
[8]谭论农.市场环境下电力系统安全性的经济实现[D].西安交通大学,2003.
[9]王锡凡,王秀丽,别朝红.电力市场条件下电力系统的可靠性问题[J].电力系统自动化,2000,25(1).
