双曲线切线的一组优美性质
2013-07-25江苏省张家港市暨阳高级中学赵颖颖
☉江苏省张家港市暨阳高级中学 赵颖颖
文[1]给出了椭圆切线的几个有关性质,笔者思考:椭圆和双曲线同为圆锥曲线,既然椭圆有这样的性质,双曲线应该也有相同的性质,或者有类似的性质.经过笔者的探究,发现答案是肯定的.现在将双曲线切线的若干性质叙述如下.
性质1 双曲线的任意一条切线平分该切点与两焦点连线段所夹的角.
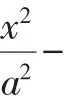
图1

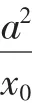
所以PT平分∠F1PF2.
若点P(x0,y0)在双曲线的左支,同理可证.
即双曲线的任意一条切线平分该切点与两焦点连线段所夹的角.
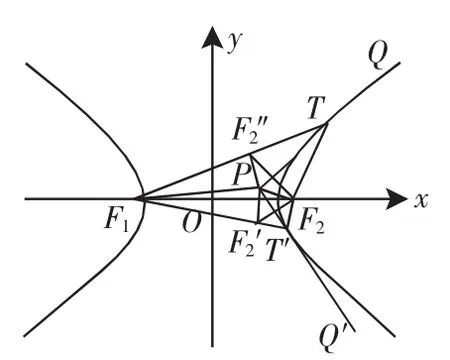
性质2 自双曲线外任一点引双曲线的两条切线,则该点与一个焦点的连线和该焦点与两切点连线段所在的直线成等角.(双曲线的两支将平面分成三部分,视不含焦点的部分为双曲线的外部)

由一定点引出的两条切线有两个可能,其一,向双曲线的两支各引一条切线;其二,向双曲线的一支引两条切线.我们分两种情况讨论:
(1)如图2所示,由点P向双曲线的两支各引一条切线PQ和PQ′,T、T′为相应的切点.
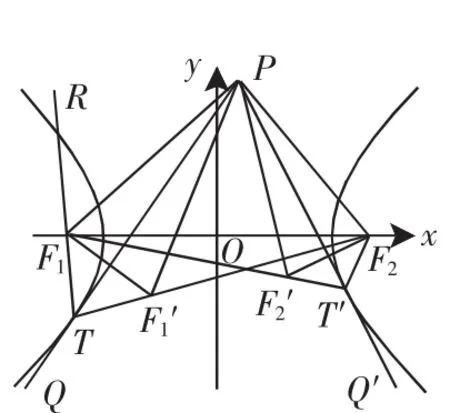
图2
作点F1关于直线PQ的对称点F1′,则∠F1TP=∠PTF1′.
又根据性质1,有∠F1TP=∠F2TP,
所以∠PTF1′=∠F2TP,所以T、F1′、F2三点共线,
同理,作点F2关于直线PQ的对称点F2′,

所以△PF1F2′≌△PF1′F2(三边对应相等),
所以∠PF1F2′=∠PF1′F2.
又因为∠PF1T=∠TF1′P,∠PF1′F2+∠TF1′P=π,所以∠PF1F2′+∠PF1T=π.
又因为∠PF1R+∠PF1T=π,所以∠PF1F2′=∠PF1R,
即PF1与F1T、F1T′所成的角相等.
同理PF2与F2T、F2T′所成的角相等.
(2)如图3所示,由点P向双曲线的一支引两切线PQ和PQ′,T、T′为相应的切点.
作点F2关于直线PQ′的对称点F2′,则∠F2T′P=∠PT′F2′.
又根据性质1,有∠F1T′P=∠F2T′P,
同理,作点F2关于直线PQ的对称点F2″,
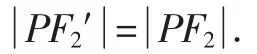
所以△PF1F2′≌△PF1F2″(三边对应相等),
所以∠PF2′F1=∠PF2″F1,∠PF1T=∠PF1T′.
即PF1与F1T、F1T′所成的角相等.
又因为∠PF2′F1+∠T′F2′P=π,∠PF2″F1+∠TF2″P=π,
所以∠T′F2′P=∠TF2″P.
又因为∠T′F2′P=∠T′F2P,∠TF2″P=∠TF2P,
所以∠T′F2P=∠TF2P.
即PF2与F2T、F2T′所成的角相等.
综合(1)、(2),于是性质2得证.
性质3 双曲线的一条动切线介于从双曲线外一定点引出的两条切线间的部分,在一个焦点的视角是常量.
由一定点引出的两条切线有两种可能,其一,向双曲线的两支各引一条切线;其二,向双曲线的一支引两条切线.下面我们分两种情况讨论:
(1)如图4所示,设PA和PB为从双曲线外一定点P向双曲线的两支各引一支的两切线,A、B为相应的切点,F2为双曲线的一个焦点,动切线CD交PA反向延长线于点D,交PB于点C,与双曲线相切于点E.
设∠AF2B=2α,因为PA和PB为定切线,所以2α为常量.
连接PF2,则由性质2可知PF2与AF2、BF2所在的直线所成的角相等,即∠PF2A=∠PF2B′.
又因为DA和DC也是双曲线的两条切线,连接DF2,
所以DF2与DA、DC所在的直线所成的角相等,即∠DF2A=∠DF2E′.
同理CD和CB也是双曲线的两条切线,故∠CF2E=∠CF2B.
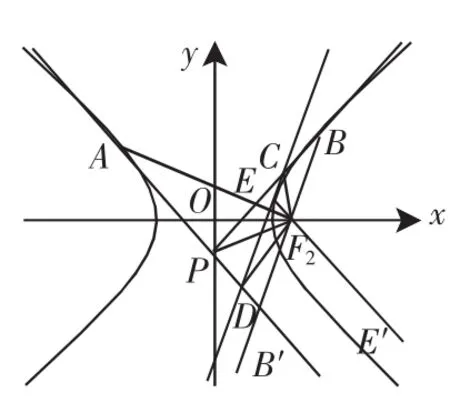
图4
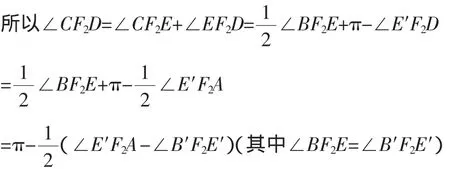

注:若2α>π,类似可证.
(2)如图5所示,设PA和PB为从双曲线外一定点P向双曲线中的一支引出的两条切线,A、B为相应的切点,F2为双曲线的一个焦点,动切线CD分别交PA、PB于点C、点D,且与双曲线相切于点E.
设∠AF2P+∠PF2B=2α,因为PA和PB为定切线,所以2α为常量.
连接PF2,则由性质2可知PF2与AF2、BF2所在的直线所成的角相等,即∠PF2A=∠PF2B.
又因为DB和DC也是双曲线的两条切线,连接DF2,CF2,
所以DF2与DB、DC所在的直线所成的角相等,即∠DF2B=∠DF2E.
同理CD和CA也是双曲线的两条切线,故∠CF2E=∠CF2A.

图5
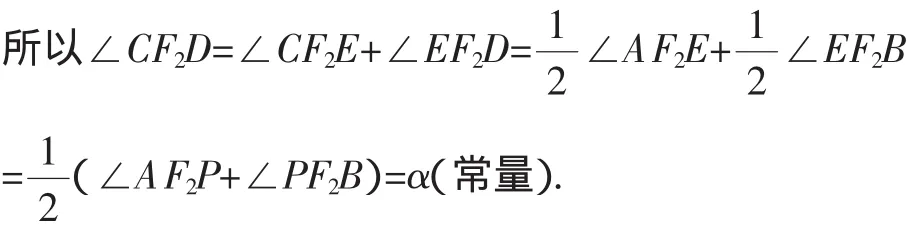
综合(1)、(2),于是性质3得证.
性质4 自双曲线的两焦点向双曲线的任一切线所引的两条垂线段长的积为定值.
故两焦点到切线的垂线段长的积为:
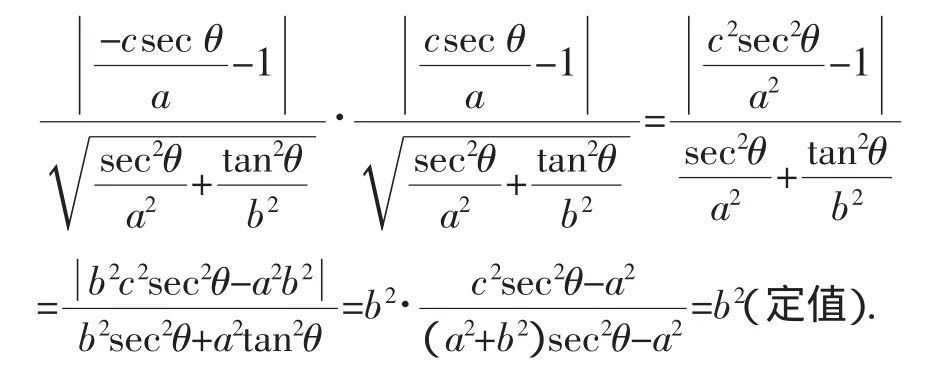
性质5 双曲线的一条动切线介于双曲线的两渐近线间的部分,在一个焦点的视角是一个常量,且视角的余弦值为双曲线离心率的倒数(或负倒数).
设切线交两渐近线于点A、B.
易得双曲线的渐近线方程分别为bx-ay=0、bx+ay=0.
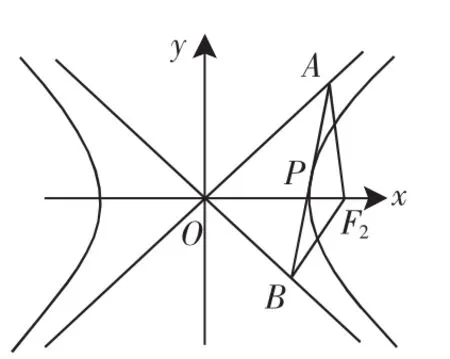
图6




于是性质5得证.
推论1 双曲线的一条动切线与双曲线的两渐近线的交点和双曲线的两焦点共圆.(证略)
性质6 双曲线的两渐近线被双曲线上任一点处的切线截得的两切线段长相等.
设切线交两渐近线于点A、B,
易得双曲线的渐近线方程分别为bx-ay=0、bx+ay=0.
由性质5证明知该切线与两渐近线的交点分别为

于是性质6得证.
性质7 双曲线的任一点处的切线与双曲线的两渐近线围成的封闭三角形的面积为双曲线实半轴与虚半轴之积.
设切线交两渐近线于点A、B,
易得双曲线的渐近线方程分别为bx-ay=0、bx+ay=0.

于是性质7得证.
1.崔宝法.椭圆切线的几个典型性质[J].数学通讯,2006(15).
