新型机械式无级变速器的设计及优化

曾 文 王玉兴 夏红梅 卿艳梅

华南农业大学，广州，510642

0 引言

机械式脉动无级变速器采用连杆（或其他类型）机构组成一个相，由至少三个相组成一个无级变速机构，通过超越离合器的过滤作用，滤掉低于某一速度值的转速，输出符合单向离合器过滤条件的转速。机械式脉动无级变速器具有传动可靠、寿命长、变速范围大、最低输出转速可为零、静止和运动中均可调速、结构简单、制造较容易等特点［1－2］。但这类脉动机械式无级变速器的基本工作机构为多套连杆机构，普遍存在以下缺陷：不平衡惯性力引起的振动大；承载能力和抗冲击能力相对较弱；脉动度较大；多相结构导致机械效率降低，磨损加剧；整机效率不高，输出功率小，不适合用于大功率场合［3－4］。为克服机械式脉动无级变速器的缺陷，国内外学者做了大量的研究工作，研究开发了多种类型的新型脉动无级变速器［5－9］，这些变速器距离实际使用越来越近。

本文利用棘轮传动具有可靠性高、传动平稳等优点，将棘轮传动与双曲柄机构组合，提出了一种新型的增速型无级变速装置。这种新型无级变速装置具有输出速度的脉动度小、整机结构简单、制造成本低的特点。

1 工作原理

1.1 传动机构原理

新型机械式脉动无级变速器的工作原理如图1所示，其主体传动机构与传统脉动无级变速器一样，也是基于连杆机构设计的。

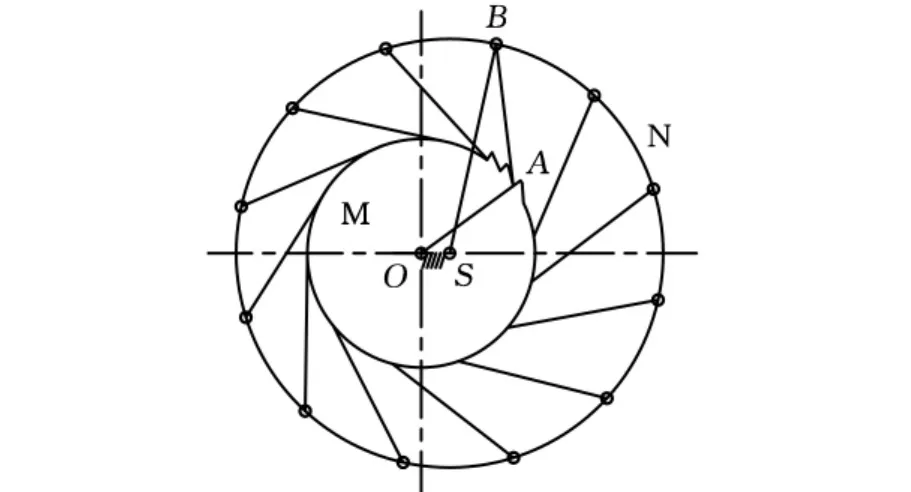
图1 棘轮传动机构原理示意图

棘轮机构由主动棘轮M、棘爪AB、从动摆杆SB（从动轮N）组成，主动棘轮逆时针转动，通过棘爪AB带动摆杆SB实现逆时针转动。在棘轮棘爪啮合传动时，该棘轮机构可以简化为四杆机构OABS。由于该机构需要实现从动摆杆SB整周连续转动，因此四杆机构OABS为一双曲柄机构，且OS为最短杆。在双曲柄机构中，从动曲柄SB的输出角速度周期性变化，且周期内速度脉动较大，不适合直接输出。为了使得从动曲柄输出的角速度脉动较小，可以采用多组相同的双曲柄机构。具体到该棘轮机构上，只需要在从动轮N和棘轮M间均匀添加多个棘爪即组成多相双曲柄机构，各相双曲柄机构的主动曲柄均为棘轮M，从动曲柄均为输出轮N。在棘轮M的转动过程中，只有从动曲柄SB转动角速度最大的一相双曲柄机构起作用，其他相机构中的棘爪AB在棘轮上滑动，从而实现超越。

分析棘轮啮合式无级变速的原理知，相对于传统脉动无级变速器，该新型无级变速器具有以下的基本特点：①棘轮作为传递运动的构件，同时又起到了超越离合器同等的效用，因而不再需要专门的超越离合器，整机结构较简单；②力的传递由传统脉动无级变速器的摩擦式改变为啮合式，力传递的可靠性得到提高；③系统中的运动部件为棘轮和外轮，因此系统的惯性力、惯性力矩较小；④每对棘轮和棘爪的啮合范围有限，等价四杆机构的工作范围相对较小，即棘轮和棘爪的相数必须较多，每相机构的输出速度均在极值附近较小的范围内，速度脉动值小，输出运动的连续性和平稳性得到较大的提升；⑤通过改变主动棘轮M和从动轮N的偏心进行无级调速，当偏心为0时，无级变速器的传动比为1；⑥该无级变速器属于增速类无级变速器。

1.2 变速机构装置设计

对于单套的棘轮啮合无级变速，需要通过调整从动外轮与主动棘轮之间的偏心来调速，所以从动外轮的轴心是变化的。为了解决该问题，可以将一套棘轮啮合无级变速机构作为输入转换机构，而使用与其共轭的一套棘轮啮合无级变速机构作为输出转换机构，两套棘轮啮合无级变速机构的外轮作为一个构件，这样，输入转换机构的从动外轮就作为输出转换机构的主动外轮，推动其棘轮实现定轴输出，无级变速器的传动比就为输入转换机构的传动比与输出转换机构传动比的乘积，无级变速器的传动比范围也得以增大。

图2所示为设计的棘轮啮合式无级变速器装置结构。运动与动力通过输入轴5传递到输入转换机构的棘轮17，由棘轮机构驱动外轮8逆时针转动。外轮8同时也是输出转换机构的主动构件，然后驱动输出棘轮19也实现逆时针的转动。变速时只需调整偏心调节杆10的摆动角度就能调节外轮8和棘轮之间的偏心，从而达到调速目的。

2 传动比分析

2.1 输入转换机构

取输入转换机构任一相的双曲柄机构进行分析，机构运动简图见图3。为说明输入转换机构的变速原理，需先推导主动曲柄OA的角速度ω1和从动曲柄SB的角速度ω3之间的关系。四杆机构的杆长设置如下：R为从动曲柄SB的长度，r为主动曲柄OA的长度，l为棘爪AB的长度，e为偏心摆杆OS的长度。

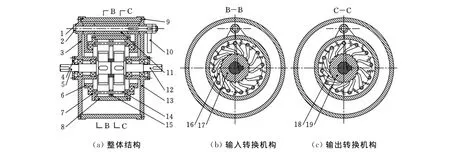
图2 无级变速器装置结构

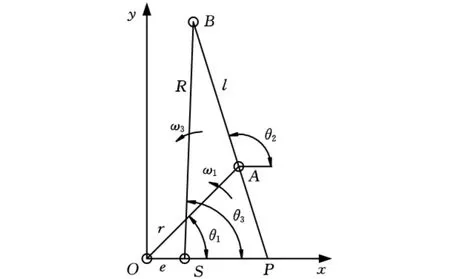
图3 输入转换机构运动简图

图3为输入转换机构运动简图，P点为曲柄OA与曲柄SB的相对瞬心。根据相对瞬心的定义，有

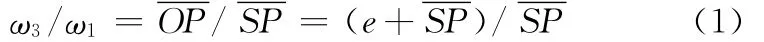
由式（1）可知，当e＝0时，四杆机构成为一个稳定的三角形，机构作为一个整体进行转动，此时输出角速度ω3与输入角速度ω1完全相同，即传动比为1；当P点在S点的右边时，ω3与ω1的比值大于1，而该输入转换机构只有在输出角速度ω3最大值附近的较小范围内起作用，因此该无级变速器为增速型调速。

基于复数矢量法可得到输入转换机构的角θ1、θ2、θ3之间的联系方程［10］：

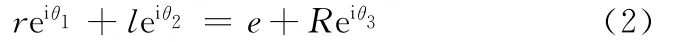
利用欧拉公式eiθ＝cosθ＋isinθ将式（2）的实部和虚部分离，并消去θ2后可得到θ3与θ1的关系如下：

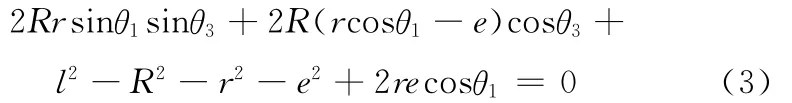
设μ1＝e/R，μ2＝r/R，μ3＝l/R，μ4＝ （μ3－μ2－μ1－1）/2，则式（3）可简化为

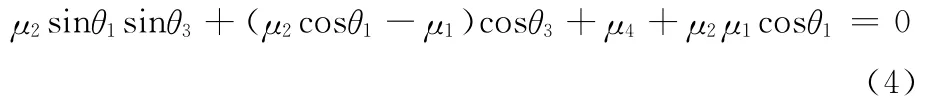
求解式（4）可得

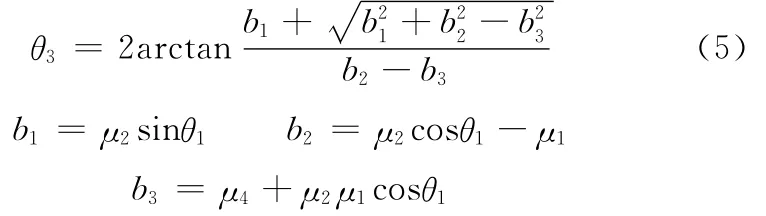
再将式（5）的θ3值代入式（2）即可得到θ2的值。

将式（2）对时间求导，可得

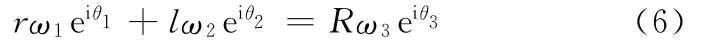
用欧拉公式将式（6）的实部和虚部分离并消去ω2后可得

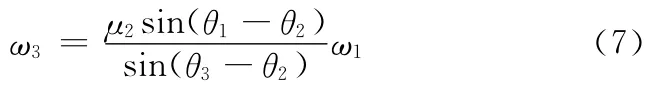
输入转换机构由多相组成，其每相作用的角度范围为360/z（z为机构相数）。图4为输入机构为多相时外轮的输出曲线图，每相作用的角度范围为a～b。由图4可知，输入机构的平均输出角速度为最大输出角速度ω3max与a点的角速度ωa的平均值：

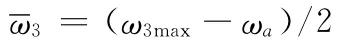
脉动度δ用输出角速度的变化幅度Δω与平均输出角速度的比值来表示，即

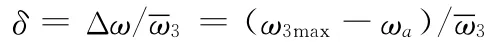
输入转换机构的平均传动比i1为

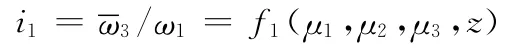
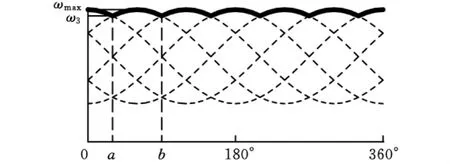
图4 多相时外轮N的输出曲线

2.2 输出转换机构

在输出转换机构中，曲柄SB变为主动构件，曲柄O′A′变为从动构件。输出转换机构运动简图见图5。与输入转换机构的计算过程类似，可以获得输出转换机构中的曲柄O′A′转角θ3、连杆A′B的转角θ2与主动曲柄SB转角θ1的关系：

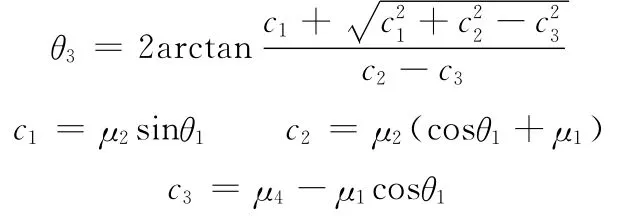
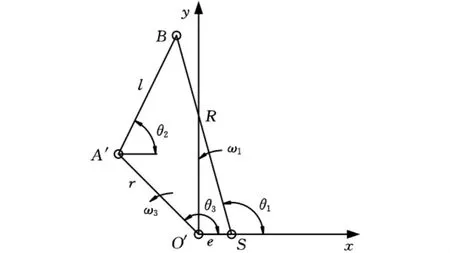
图5 输出转换机构运动简图

输出构件O′A′的角速度ω3与主动曲柄SB角速度ω1的关系为

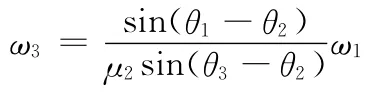
与输入转换机构一样，输出转换机构也为增速输出，其平均输出角速度和脉动度与输入转换机构公式相同，其传动比i2为

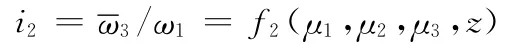
综合输入转换机构和输出转换机构的传动比，即为无级变速器的总传动比i：

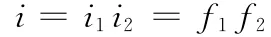
3 优化模型的建立

无级变速器优化设计的目的是在满足机构杆长条件、机构尺寸限制、传动角限制的前提下，获得最大的增速传动比［11-12］。

3.1 设计变量

从输入转换机构传动比和输出转换机构传动比的分析中可知，输出构件的最大转速取决于各杆的杆长。由于设计时外轮半径一般根据传动的功率和整机尺寸限制来选取而作为已知值，所以可以使用各杆杆长作为优化设计的设计变量。设计变量定义为：μ1＝e/R，μ2＝r/R，μ3＝l/R。

3.2 目标函数

与一般脉动式无级变速器的脉动度相比，棘轮啮合式无级变速器的脉动度显然要小很多，其转速脉动基本上可以忽略。以实现无级变速器传动比最大为出发点建立目标函数。当双曲柄机构的各杆杆长固定时，输入转换机构和输出转换机构的传动比是不变的。换言之，在外轮半径R不变时，输入转换机构传动比i1和输出转换机构的传动比i2是随设计变量μ1、μ2、μ3变化的，因此可建立无级变速器传动比最大的优化目标函数如下：

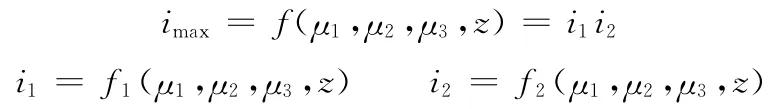
3.3 约束条件

考虑机构必须满足双曲柄的存在条件，存在以下约束：

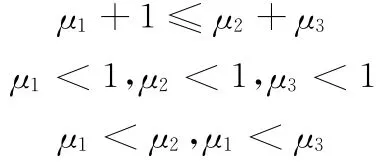
为了保证啮合传动的过程中棘轮与棘爪、棘爪与外轮之间不产生干涉，需要设定如下的约束关系：

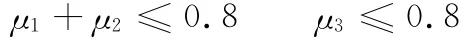
为保证双曲柄机构在啮合范围内能顺利地运动，其传动角应在许可的范围内。工程中常取传动角许可范围为30°～150°。

对于图3所示的输入转换机构，由余弦定理可得依传动角许可范围条件，可得

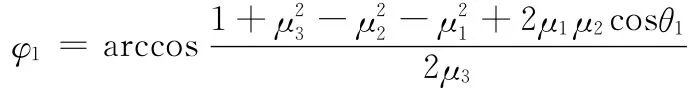
30°＜φ1＜150°

对于图5所示的输出转换机构，由余弦定理可得

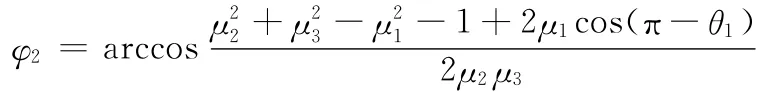
依传动角许可范围条件，可得

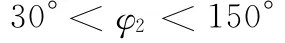
3.4 优化结果

使用C＃语言编写的优化程序的人机界面见图6。以外轮半径60mm、机构相数12为例，获得机构优化参数如下：r＝40mm，l＝44mm，e＝9mm，最大传动比imax＝1.5785，脉动度δ＝2.15%。由优化结果可知，该类型的无级变速器增速范围不大，但其转速的脉动度相对于传统4相或6相的无级变速器脉动度18%［12］就小很多。

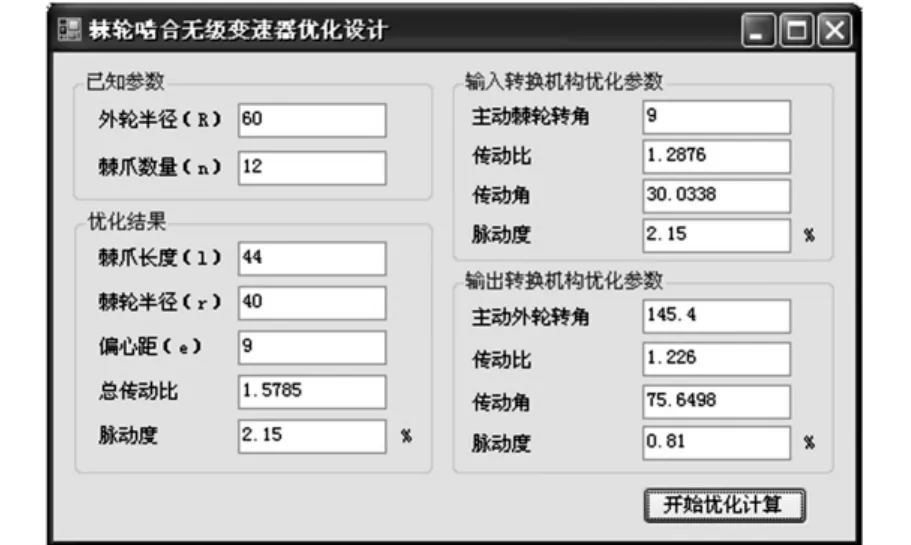
图6 人机交互优化设计界面

4 结论

（1）结合棘轮机构和双曲柄机构的特点，设计了一种新型的棘轮啮合式无级变速器，该无级变速器具有结构简单、传动可靠性高、脉动度小的特点，是一种增速型的无级变速器。

（2）运用解析几何及机构综合的方法建立了无级变速器输入转换机构和输出转换机构的机构综合模型，为该无级变速器的传动比计算提供了依据。

（3）建立了以实现无级变速器传动比最大为目标函数，双曲柄的存在条件、机构尺寸限制、传动角限制等为约束条件，机构杆长为设计变量的优化设计模型，编写了优化设计程序。优化示例结果表明，该类无级变速器的脉动度小，但传动比范围有限。

［1］周有强.机械无级变速器［M］.北京：机械工业出版社，2001.

［2］周有强，崔学良，董志峰.机械无级变速器发展概述［J］.机械传动，2005，29（1）：65－68.

Zhou Youqiang，Chui Xueliang，Dong Zhifeng.Development Overview of Mechanical Continuously Variable Transmission［J］.Journal of Mechanical Transmission，2005，29（1）：65－68.

［3］聂松辉，刘宏昭，邱爱红.新型非摩擦式机械无级变速器的原理与特性［J］.机械工程学报，2007，43（9）：191－194.

Nie Songhui，Liu Hongzhao，Qiu Aihong.Principle and Characteristics for Original Non－frictional Mechanical Continuously Variable Transmission［J］.Chinese Journal of Mechanical Engineering，2007，43（9）：191－194.

［4］杜力，黄茂林，李太福.脉动式无级变速器真实运动规律的研究［J］.中国机械工程，2004，15（12）：1080－1084.

Du Li，Huang Maolin，Li Taifu.Study on the Real Motion Law of Impulse Variable Speed Device［J］.China Mechanical Engineering，2004，15（12）：1080－1084.

［5］冯云华，杜力，黄茂林.非摩擦式连续作用无级变速器的结构创新及设计［J］.重庆大学学报，2003，26（9）：43－46.

Feng Yunhua，Du Li，Huang Maolin.Design of Non－frictional Variable Speed Driver with Continuous Action［J］.Journal of Chongqing University，2003，26（9）：43－46.

［6］聂松辉，刘宏昭，邱爱红.新型脉动式无级变速器研究［J］.华南理工大学学报，2007，35（8）：44－48.

Nie Songhui，Liu Hongzhao，Qiu Aihong.Development of Novel Pulsed Mechanical Continuously Variable Transmission［J］.Journal of South China University of Technology（Natural Science Edition），2007，35（8）：44－48.

［7］卢军平.齿轮式脉动无级变速器改进与结构优化设计［D］.苏州：苏州大学，2011.

［8］王树春，车仁炜，徐伟国.一种新型的机械无级变速器［J］.机械设计，2004，21（4）：56－59.

Wang Shuchun，Che Renwei，Xu Weiguo.A Novel Mechanical Continuously Variable Transmission［J］.Journal of Machine Design，2004，21（4）：56－59.

［9］毛志伟，张华.一种新型脉动式无级变速器机构运动分析与运动仿真研究［J］.机械传动，2005，29（3）：44－46.

Mao Zhiwei，Zhang Hua.Reaserch on the Mechanism Motion Analysis and Motion Display of the New Style Pulse Stepless Transmission［J］.Journal of Mechanical Transmission，2005，29（3）：44－46.

［10］孙恒，陈作模.机械原理［M］.北京：高等教育出版社，2004.

［11］徐彦兰，王玉顺.曲柄摇杆式脉动无级变速器的机构参数优化［J］.山西农业大学学报（自然科学版），2010，30（4）：363－370.

Xu Yanlan，Wang Yushun.The Optimal Design of Impulse Steeples Speed Variation［J］.Journal of Shanxi Agricultural University （Natural Science Edition），2010，30（4）：363－370.

［12］赵鹏云，黄茂林，杜力，等.脉动值恒定的新型无级变速器的优化设计［J］.重庆大学学报（自然科学版），2005，28（9）：9－12.

Zhao Pengyun，Huang Maolin，Du Li，et al.Optimum Design of New Style Impulse Variable Speed Device Based on Invariable Impulse Value［J］.Journal of Chongqing University（Natural Science Edition），2005，28（9）：9－12.