汽车自动调整臂螺旋压缩弹簧的失效建模

罗 哉 江文松 陆 艺 胡晓峰

中国计量学院，杭州，310018

0 引言

汽车制动间隙自动调整臂（以下简称自调臂）是汽车制动系统中的关键部件。汽车在频繁制动下，制动衬片和制动轮毂之间预设的间隙（以下简称蹄毂间隙）就会因制动衬片的磨损而增大。自调臂能自动补偿增大的蹄毂间隙［1］，从而使汽车在任意制动情况下都能保持正常的制动效果，避免出现制动力不足甚至侧翻等失效情况的发生［2］。

自调臂自调功能的失效是制动性能长期稳定的严重威胁，失效一旦发生，将严重影响汽车的制动效果，甚至会引起交通事故，给社会生产和生命财产带来不必要的损害。

本文针对引起自调功能失效的机械结构建立了故障树模型，分析了可能引起失效的所有事件，重点研究了螺旋压缩弹簧的失效所诱发的自调功能失效的情况，建立了该系统下失效的力学模型。该失效模型将有助于自调臂的结构特性优化，有助于检测行业研发合理有效的自调臂性能检测设备，以完善自调臂的性能。

1 自调臂的机械结构和工作原理

1.1 自调臂机械结构组成

如图1所示，自调臂的结构主要由壳体7、蜗轮蜗杆（6，11）、单向离合器（2，3，4）、齿轮齿条传动机构（4，8）、控制盘与控制臂（9，10）以及三组重要的弹簧（3，13，15）等结构组成［3－5］。

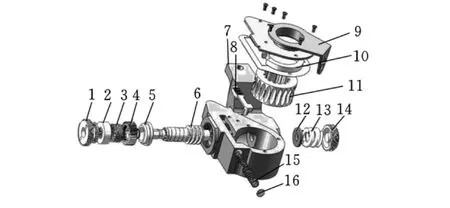
图1 自调臂结构图

蜗杆左侧装配单向离合器，单向离合器自左向右由离合环、离合弹簧和齿轮组成。单向离合器中的离合环有内锥齿，与蜗杆端面的外锥齿轮构成锥形离合器。受蜗杆右端的螺旋压缩弹簧作用，锥齿轮通过保持或释放啮合状态来传递力矩。

1.2 自调臂工作原理

自调臂通过间隙感知原理保证制动器蹄毂间隙的恒定。在制动回位过程中，感知与蹄毂间隙的超量值相对应的自调臂的角行程，并自动加以微调补偿。而弹性角行程（制动衬片与制动轮毂的接触使传力元件产生弹性变形的角行程）则不予调整［6］，如图2所示。其中，C为正常制动间隙角行程，即预设的蹄毂间隙；Ce为超量间隙角行程，即制动衬片因磨损产生的蹄毂间隙的增大量；E为弹性角行程。

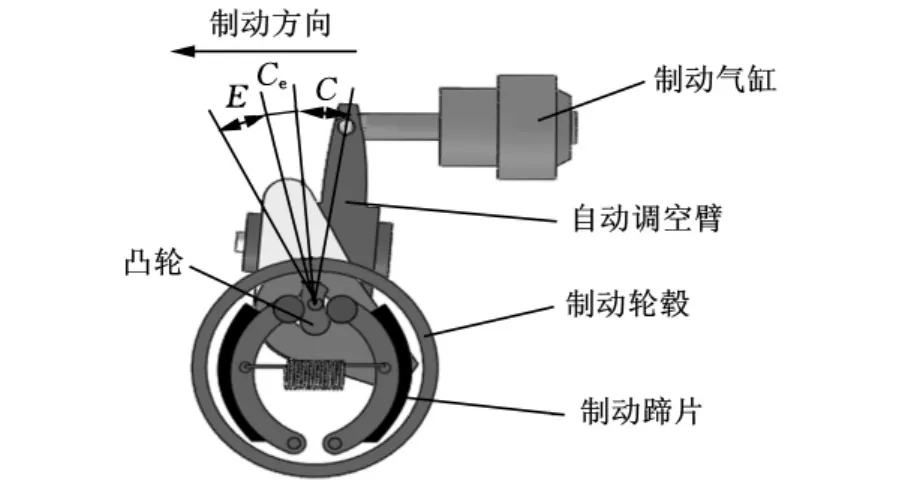
图2 制动器中自调臂的转角构成

制动前，齿条后端与单向离合器的齿轮啮合，前端的突起嵌在控制盘的缺口内。突起紧贴缺口后边沿，缺口大小对应于正常制动间隙的转角C。制动时，控制盘作为定位器件，齿条则会从缺口的后边沿滑向缺口前边沿。

超量间隙的调整是在制动回位的过程中完成的。回位时，壳体带动齿条向缺口的后边沿移动。如果制动衬片发生磨损，蹄毂间隙存在超量值，壳体将继续回位，齿条的突起由于被缺口后边沿挡住而不能继续后退，从而推动与齿条啮合的离合齿轮转动，使单向离合器沿顺时针方向转动超量间隙对应的角行程，并使蜗杆驱动蜗轮沿逆时针方向转动一个永久的角度，从而消除超量间隙，调整蹄毂间隙到预设标准值。

2 螺旋压缩弹簧的失效建模

2.1 构建自调功能的故障树

基 于 故 障 树 分 析 法 （fault tree analysis，FTA）将组成自调臂的结构系统的零件定义为组元，自调臂的自调功能用来描述系统的部分功能特性［7－8］。自调臂自调功能的失效属于竞争失效模式，若系统的任一组元失效，都将导致系统功能的失效［9］。根据实现自调功能的结构构成，建立自调功能失效的故障树模型，如图3所示。

螺旋压缩弹簧的压紧状态对保持单向离合器与蜗杆锥齿轮啮合起到关键性作用，一旦螺旋压缩弹簧因失效导致弹簧力不足，就会引发锥形离合齿轮因轴向推力小而打滑，导致涡轮的自调量不足，最终引起自调功能失效。

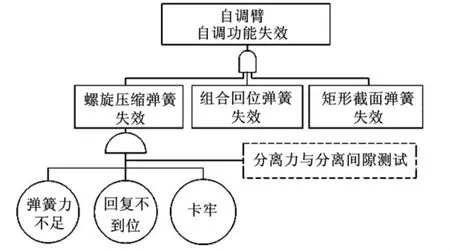
图3 自调臂的故障树

利用分离力与分离间隙测试系统实时测试螺旋压缩弹簧的分离力和分离间隙值，据此计算判断该弹簧是否会引起打滑。再利用调整力矩测试系统测试自调臂的正反转力矩，根据力矩值验证离合器锥齿轮打滑与否。根据自调臂的工作原理，如果力矩明显小于标准值则证明离合器锥齿轮打滑。

2.2 螺旋压缩弹簧的失效形式和失效模型分析

螺旋压缩弹簧经过长期受压，往往会发生弹力不足、回复不到位、卡牢等塑性变形失效［10］，如图3所示。为了定量分析弹簧的失效特征，根据虎克定律分析弹簧的应力随其劲度系数变化的关系，从而判断失效发生的临界点。

2.3 建立失效的力学模型

自调臂的螺旋压缩弹簧为圆截面圆柱压缩弹簧。蜗杆施加在螺旋弹簧上的轴向载荷为F，其作用线与弹簧的螺旋中心线重合，螺旋角α一般取5°～9°，此时cosα≈1，sinα≈0。

根据虎克定律，弹簧的载荷F与弹簧的压缩量Δx成线性关系，即

式中，k为弹簧的劲度系数，即弹簧的刚度；n为弹簧的工作圈数；d为弹簧丝的直径；D为弹簧中径；G为弹簧材料的切变模量；c为弹簧的旋绕比。

自调臂的分离力必须大于单向离合器锥齿轮的轴向力Fa才能保持离合器齿轮的啮合状态，此时，Fa≤kΔx。因此有

式（3）表明，弹簧的刚度与弹簧的旋绕比c成反比。因此在弹簧选型时，弹簧的旋绕比不能过大。

弹簧在载荷作用下，总应力主要由剪切力产生的剪切应力和扭矩产生的扭转剪切应力组成。另外，弹簧的曲率对剪切应力也会产生很大的影响，因此在计算应力过程中还要考虑剪切应力集中系数κτ（即曲度因子）的影响，弹簧的最大剪切应力有如下关系［11］：

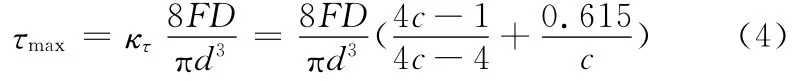
弹簧受压下，压缩变形量为

联立式（4）、式（5），弹簧的最大压缩变形量为

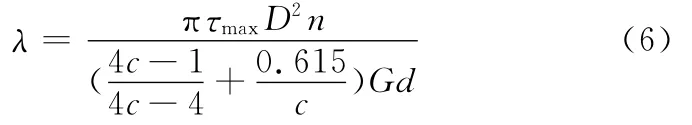
自调臂在安装过程中，螺旋压缩弹簧对蜗杆施加的预紧力所引起的位移量以及壳体与蜗杆之间的相对微小位移量共同构成了弹簧的预压缩量ε。设分离间隙值为l，弹簧的变形量应大于这两种情况下的总压缩量［12］，即λ≥l＋ε。显然，由式（1）得ε＝Fs/k，即

分析式（5）可知，弹簧的力特性受弹簧丝直径、弹簧中径、弹簧圈数及其材质的影响都较大。一旦弹簧的上述指标不满足载荷要求，弹簧将因过载而产生塑性变形，弹簧的刚度将随特性曲线的奇异而改变。代入各项参数，联立式（3）、式（7），就可以根据螺旋压缩弹簧的失效临界判断自调臂自调功能失效的临界条件。

3 实验与结果分析

实验在图4所示的综合性能检测系统中进行，该实验系统使用精度达0.1%的BK－2B型力传感器和扭矩测量精度达0.3%的JN338型扭矩传感器，系统测量标准不确定度为±0.01N·m。由于在该装置中，对自调臂扭矩和力的测量不能直接放在工作台上进行，因此需要设计专门的夹具，用以压紧自调臂。为了使自调臂的分离力与分离间隙的测试结果与实车环境下的动态参数吻合，自调臂的夹具完全按照实车的安装环境设计，从而消除测试环境对螺旋压缩弹簧失效模型准确性的影响。实验步骤如下：

（1）分离力与分离间隙测试。将自调臂装入夹具3中并启动薄型气缸5压紧自调臂，伺服电机10推动伺服平移装置8接近自调臂，使推杆接触在自调臂2的蜗杆的六方头上，当力传感器6的值达到设定值时，伺服平移装置立即停止移动，扭矩伺服电机9带动推杆转动90°角，使自调臂的蜗杆的六方头对准推杆的六方孔，之后伺服平移装置带动推杆退回至力为零处。伺服电机10带动伺服平移装置压缩自调臂的蜗杆至力为8k N处，同时计算机实时绘制出力－位移曲线，计算出自调臂的分离力和分离间隙值。分离力与分离间隙测试的曲线如图5所示。

图4 综合性能测试系统

图5 分离力与分离间隙测试曲线

（2）调整力矩测试。将转轴导入自调臂蜗杆的六方头内（对准方式同上），启动检测开关，计算机实时显示扭矩传感器检测的扭矩并绘制出扭矩－角度曲线，计算调整力矩正转最大值和反转最小值，其特性曲线如图6所示。

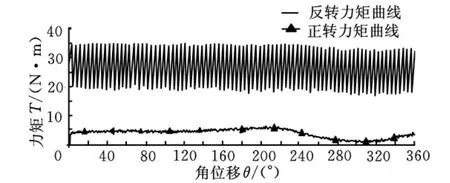
图6 调整力矩测试曲线

某自调臂的螺旋压缩弹簧材质为合金弹簧钢丝，其参数如下：弹簧丝直径d＝7mm；圈数n＝4；中径D＝20mm；旋绕比c≈2.7；通过查机械标准手册［13］，G＝78.7GPa。利用上述测试系统，对15个使用时间不同的该型号自调臂进行测试，每个自调臂测量5次取平均值。实验结果见表1。

4 结论

（1）表1的测试结果表明，当螺旋压缩弹簧刚度在4918.75≤k≤738 120时，反转扭矩T＞20N·m，即自调功能正常，而通过模型得出的结果与实验测试数据一致。

表1 自调臂失效模型的理论结果与测试值的对比

（2）当螺旋压缩弹簧的刚度k≥1 012 510时，在蜗杆反转推开啮合的锥齿轮时，因分离行程大于其变形量，导致弹簧塑性变形失效，调整力矩减小。模型验证的结果与实验数据一致。

（3）当螺旋压缩弹簧的刚度k≤2014.72时，蜗杆会因轴向推力不足导致离合器锥齿轮打滑，反转力矩骤减，制动器的自调量不足引起自调功能失效。上述模型的结果与实验测试数据一致。

（4）本模型从理论上揭示了自调臂自调功能失效的根源为所在结构处的弹簧失效，这为自调臂的结构优化及其性能、寿命检测提供了参考。

（5）本模型的构建只考虑了常温理想环境下的失效因素。根据中华人民共和国建设部CJ/T242－2007标准规定，自调臂的失效还需要考虑盐性、粉尘、极限温度等环境因素的影响和材质耐久性等时间因素的影响。今后可以综合考虑在以上几种复杂环境下的自调臂失效模型的构建。

［1］中华人民共和国建设部.CJ/T242－2007城市客车外置式制动间隙自动调整臂［S］.北京：中国标准出版社，2007.

［2］卢少波，李以农，郑玲.基于制动与悬架系统的车辆主动侧翻控制的研究［J］.汽车工程，2011，33（8）：669－675.

Lu Shaobo，Li Yinong，Zheng Ling.A Study on Vehicle Active Rollover Control Based on Braking and Suspension Systems［J］.Automotive Engineering，2011，33（8）：669－675.

［3］郝金城，卢春雷，蔡旭东.刹车间隙自动调整臂［J］.重型汽车，1996，33（2）：18－20.

He Jincheng，Lu Chunlei，Cai Xudong.Automatic Slack Adjuster［J］.Heavy Daty Truck，1996，33（2）：18－20.

［4］邱国锋，罗哉，林敏.汽车自动调整臂自调功能检测系统设计［J］.中国计量学院学报，2011，22（3）：212－216.

Qiu Guofeng，Luo Zai，Lin Min.Design on Detecting System for the Automatic Adjustment Function of Automatic Slack Adjuster［J］.Journal of China University of Metrology，2011，22（3）：212－216.

［5］刘宁霞，罗哉，邱国锋.自动调整臂寿命检测与评价系统［J］.中国计量学院学报，2012，23（2）：120－124.

Liu Ningxia，Luo Zai，Qiu Guofeng.Test and Evaluation System for Automatic Slack Adjuster Lifetime［J］.Journal of China University of Metrology，2012，23（2）：120－124.

［6］王军，赖峰.制动间隙自动调整臂的设计原理［J］.汽车科技，2006，2（2）：7－9.

Wang Jun，Lai Feng the Design Principle for Autoadjustable Arm［J］.Auto Mobile Science ＆ Technology，2006，2（2）：7－9.

［7］史定华，徐峰.FTA的若干问题与进展［J］.自动化学报，1986，12（3）：315－322.

Shi Dinghua，Xu Feng.Problems and Development of FTA［J］.Acta Automatica Sinica，1986，12（3）：315－322.

［8］Papadopoulos Y.Model－based System Monitoring and Diagnosis of Failures Using State Charts and Fault Trees［J］.Reliability Engineering and System Safety，2003（81）：325－341.

［9］李春洋，陈循，易晓山.考虑共因失效的多态系统可靠性优化［J］.中国机械工程，2010，21（2）：155－159.

Li Chunyang，Chen Dun，Yi Xiaoshan.Reliability Optimization of Multi－state System in Presence of Common Cause Failures［J］.China Mechanical Engineering，2010，21（2）：155－159.

［10］叶定奇，廉斌.初论压缩弹簧失效及预防措施［J］.机械管理开发，2006，2（2）：87－89.

Ye Dingqi，Lian Bin.Discussion on Pressure Spring Malfunction and Prevention［J］.Mechanical Management and Development，2006，2（2）：87－89.

［11］吴波，黎明发.机械零件与系统可靠性模型［M］.北京：化学工业出版社，2002.

［12］桑楠.S形凸轮制动间隙自动调整臂工作原理及运动仿真［D］.武汉：武汉理工大学，2003.

［13］机械工程师手册编委会.机械工程师手册［M］.北京：机械工业出版社，2007.