基于Taguchi方法的车门结构稳健性优化
2013-07-25洪健程
谢 晖 刘 行 洪健程
1.湖南大学汽车车身先进设计制造国家重点实验室,长沙,410082
2.苏州金鸿顺汽车部件股份有限公司,张家港,215600
0 引言
在汽车车门系统研发中,为了缩短新产品开发的周期,降低研发成本,计算机模拟仿真与优化算法结合成为了重要的设计分析手段。国内外学者很早就将该方法应用于车门系统的设计中[1-3],获得了比较好的结果。事实上,车门在制造和使用过程中存在许多不确定性因素,如制造精度、材料特性以及载何工况等,导致车门的品质特性响应(如刚度、强度和模态等)表现为概率分布,可能使设计超出约束条件而失效[4]。
随着稳健设计在许多领域的广泛应用和取得显著的实际成效,研究人员也将稳健设计方法引入到汽车工业中。文献[5-6]采用田口方法(Taguchi method)进行车门系统稳健设计;文献[7]采用基于6σ质量工程的稳健设计方法,分别对汽车侧面碰撞性能和乘员约束系统进行稳健性优化;文献[8-10]采用双响应面法对汽车碰撞安全性能进行稳健性优化。在汽车工业中,稳健设计主要有三种方法:第一种是田口方法;第二种是基于6σ质量工程的稳健设计方法;第三种是双响应面法。田口方法主要基于正交设计和SN比设计,计算分析流程规范,应用范围广,已有很多成功的案例。基于6σ质量工程的稳健设计方法通过使质量特性远离边界约束,达到6σ水平,保证质量特性稳定。该方法需要不断地计算质量特性的均值和标准差,在大多数情况下,这两个值比较难确定,一般通过抽样模拟的方法获取,但计算效率和精度存在一定的问题。双响应面法将质量特性的均值和标准差各自用一个响应面进行拟合,然后对响应面模型进行优化求解获得稳健解。该方法数学法则严谨,计算精度高。由于后续的分析和计算都是基于响应面模型进行的,因此响应面模型的拟合精度与计算结果的好坏直接相关。针对不同的问题,响应面类型和样本点的选取并没有统一的规则。该方法对工程技术人员要求较高。比较而言,田口方法由于计算分析流程规范,在工程上得到了更为广泛的应用。
目前,针对汽车车门结构性能稳健性优化的研究相对较少。文献[5-6]采用田口方法进行车门结构优化,因没有考虑不确定性因素的影响,最后得到的并不是最稳健的解,而只是较优解。文献[10]基于6σ质量工程的稳健设计方法进行车门的轻量化稳健性设计,设计中虽考虑了车门板料尺寸的不确定性,但因没有考虑材料特性与载荷工况的不确定性影响,设计也难尽如人意。本文从工程应用角度出发,适用田口方法中的参数设计方法,考虑材料特性与载荷工况的不确定性,对处于详细设计阶段的车门进行稳健性优化,设计在减轻车门重量的同时,提高了车门结构性能的稳定性。本文方法具有较强的工程实用性。
1 Taguchi方法
Taguchi方法主要由系统设计、参数设计和容差设计三个阶段的设计组成,亦称为三段设计或三次设计。三次设计是运用专业技术和试验设计技术,特别是SN比试验设计,开发和设计功能稳定、质量优良的产品[11-12]。
(1)系统设计。系统设计是应用专业技术进行系统或产品的功能设计和结构设计。一个系统或一种产品,其要由哪些子系统、哪些零部件组成,采用什么结构,如何把子系统、零部件组合起来,功能目标值的水平如何属系统设计应考虑的范畴。
(2)参数设计。参数设计是确定系统或产品中各个参数的最佳水平及其组合的阶段。参数设计可以运用一部分波动大的原材料、零件与加工条件,设计出目的特性稳定的优良产品。参数设计实质上是运用试验设计技术进行的优化设计,是整个设计过程中的核心阶段。
(3)容差设计。容差设计就是在参数设计时决定了各参数中心值后,再对中心值规定出容许差(公差的一半)。容差设计的目的在于衰减或缩小由各种干扰所引发的目的特征值的波动,确定各元器件、零部件应选用的品级,规划产品的质量与成本。
1.1 SN比
SN比起源于通信领域,作为评价通信设备、线路、信号质量等优劣的指标,采用信号(signal)的功率与噪声(noise)的功率之比,即SN比,作为指标,其单位为dB(分贝)。田口教授在稳健性设计中引入SN比作为评价设计优劣的一种测度,也作为产品质量特性的稳定性指标,已成为稳健设计中的重要工具。SN比在不同场合具有不同的计算公式。
望目特性的SN比表达式为

望小特性的SN比表达式为

望大特性的SN比表达式为

式中,yi为质量特性的测量值;n为测量值的个数。
1.2 参数设计的主要步骤
Taguchi方法中参数设计的主要步骤如下:
(1)根据设计要求,确定产品性能指标、控制因素以及误差因素。
(2)确定控制因素和误差因素的水平,一般取三水平为宜。
(3)选择合适的正交表,将控制因素配列于内表,误差因素配列于外表。
(4)依照正交表的组合处理,通过计算和试验得到产品性能指标。
(5)计算SN比的η值,记入内表数据栏。
(6)对η值进行统计分析,选出最佳设计条件。
(7)对最佳设计条件进行验证计算或试验。
图1所示为参数设计具体实施步骤。
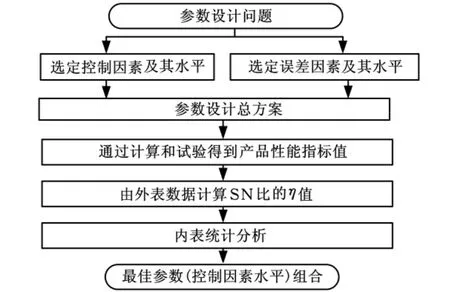
图1 参数设计框图
2 算例研究
2.1 车门有限元模型及工况简述
车门的有限元模型如图2所示,采用壳单元划分网格,网格大小为10mm。模型包含60 351个单元,其中四边形单元为39 201个,三角形单元为1284个(占单元总数的2.1%)。车门各板之间的点焊连接用Cweld单元模拟,车门防撞梁与外板间的胶接用Solid实体单元模拟。

图2 车门有限元模型和下垂刚度工况
汽车车门应具有足够的刚度、强度和良好的抗振特性,以保证汽车的安全性和乘坐舒适性[10]。车门的刚度一般包括下垂刚度、上扭刚度和下扭刚度。
车门下垂刚度分析加载方式如图2所示,约束车门副铰链6个方向的自由度以及锁心处Y向的平动自由度,主副铰链之间放开绕Z轴的旋转自由度,在锁心处施加900N的Z向力。车门上扭刚度的加载方式为:在窗框边线以下5mm施加900N的Y向力。约束车门副铰链6个方向的自由度,主副铰链之间放开绕Z轴的旋转自由度;约束锁心X、Y、Z方向的3个移动自由度。车门下扭刚度的加载方式为:在内板下部圆角中心处施加900N的Y向力。约束方式与计算上扭刚度时相同。
对原车门模型进行刚度分析,得到的结果如表1所示。
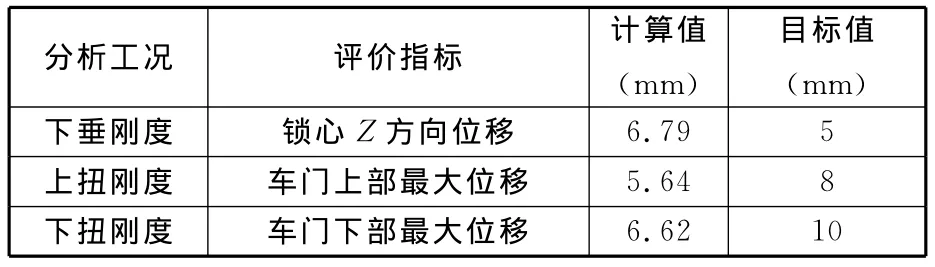
表1 原车门模型刚度分析结果
由表1可知,车门的下垂刚度不满足设计要求。另外,根据该车型整车模态规划表,车门一阶固有频率应大于35Hz,否则可能与车身低阶模态耦合共振。经计算,原车门的一阶固有频率为33.91Hz,不满足设计要求。因此需要对该车门的下垂刚度和一阶固有频率进行优化设计。由于车门上扭刚度和下扭刚度与目标值间有较多的余量,为了降低问题的复杂程度,故在优化分析时暂不考虑,只对最终结果进行验证分析。
2.2 试验方案设计
根据设计要求及专业技术分析,选取车门中7个板件的厚度作为控制因素。每个因素对应3个水平,如表2所示。如果按照7因素和3水平进行全因子试验,则需要进行37=2187次试验。计算量非常大,评估和处理这些组合需要花费大量的时间和精力。基于正交试验的Taguchi参数设计方法,能用较少的试验次数,获得理想的评价结果。选用正交表的原则是:只要试验因素能安排得下,就尽可能用小号正交表。根据因素和水平的数目,选用不等水平正交表L18(6×37)。最终到得的内表试验方案如表3所示。第一列没有安排控制因素,用来考查试验误差的影响。

表2 控制因素及水平 mm

表3 内表设计
对于误差因素,本例考虑了材料密度ρ和弹性模量E的不确定性以及下垂刚度试验中加载力F的波动对试验结果的影响。误差因素的波动范围分别为

参数设计中,误差因素以取三水平为宜。依据因素和水平的数目,需要选用正交表L9(34)作为外表。整个参数设计中,总的试验次数为内表的试验次数乘以外表的试验次数,即18×9=162次。这也是一个比较大的计算量。为了减少外表设计中的试验次数,本文采用文献[13]提出的二水平正交设计方法进行正交设计。误差因素波动范围的下界和上界分别为第1和第2水平。选用正交表L4(23),得到的外表试验方案如表4所示。
将表3的内表和表4的外表直积起来,分别得到关于车门下垂刚度和车门一阶固有频率的直积设计表,如表5、表6所示。显然,直积设计共有18×4=72种组合,计算的工作量大大减少。采用组合工况,可在单次有限元计算中同时获得车门下垂刚度中的锁心Z向位移量和一阶固有频率。在Isight软件中设置好试验设计方案,通过调用有限元分析软件Nastran,自动完成72次有限元分析。在一台主频为2.8GHz,内存为3G的双核电脑上计算,共耗时3.75h。锁心Z向位移量计算结果见表5,车门一阶固有频率计算结果见表6。

表4 外表设计
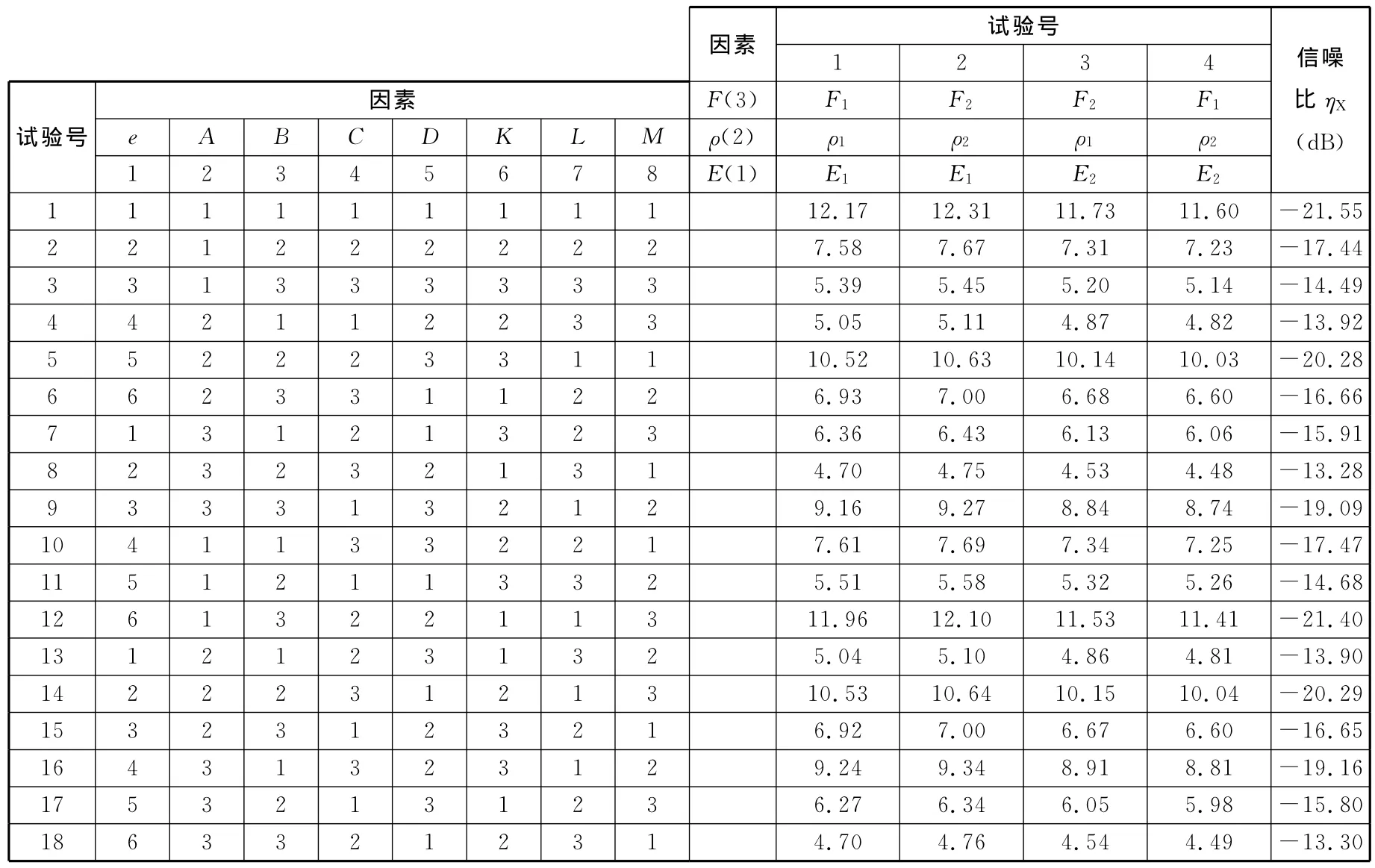
表5 车门下垂刚度直积设计与试验数据

表6 车门一阶固有频率直积设计与试验数据
2.3 试验结果分析
首先计算SN比,如欲求内表的第1号试验条件的SN比,即取外表第一行的4个数据进行计算。同样地,可求得内表其余试验条件的SN比。对于锁心Z向位移量,车门下垂刚度越大,则锁心Z向位移量越小,为望小特性。SN比按式(2)计算。车门一阶固有频率为望大特性,SN比按式(3)计算。最终得到的锁心Z向位移量SN比和车门一阶固有频率SN比分别见表5和表6。
通过SN比方差分析可以判断控制因素的主次与显著性,从而确定最优组合及其置信区间。对表5和表6中的SN比分别进行方差分析,得到的分析结果如表7和表8所示,表中的Fb为方差齐性检验的计算值。方差分析表中各偏差平方和及其自由度的计算公式为
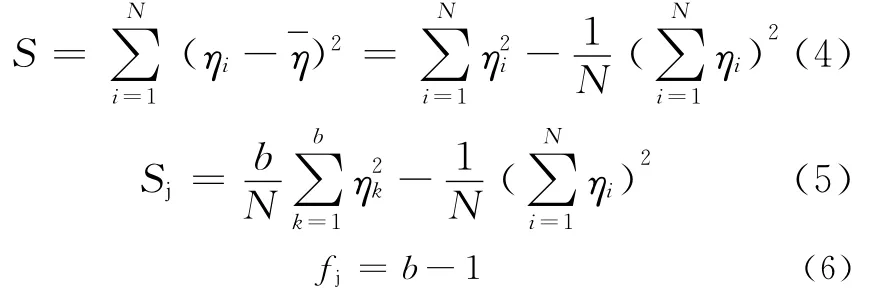
并且

式中,ηi为望目、望小和望大的SN比;ηk为第k水平对应的η合计值;Sj为控制因素的主效应及其波动值或偏差平方和;b为控制因素水平数;N为内表试验次数;Se为空列的偏差平方和;fe为(等于)空列的水平数减1,即fe=6-1=5。

表7 锁心Z向位移量SN比方差分析表
在质量设计中,通常把显著性水平α≤0.05的因素作为显著因素,最佳组合就是显著因素都取优水平的组合。至于非显著因素则权衡利弊,综合考虑选取适当水平[12]。由表7可以看出,对锁心Z向位移量,控制因素A、L是显著的。由表8可以看出,对车门一阶固有频率,只有控制因素A是显著的。由于SN比大的因素水平为优,故SN比大的优水平组合即为最佳组合。对显著因素各水平对应的η平均值进行计算,结果如表9所示。

表8 车门一阶固有频率SN比方差分析表
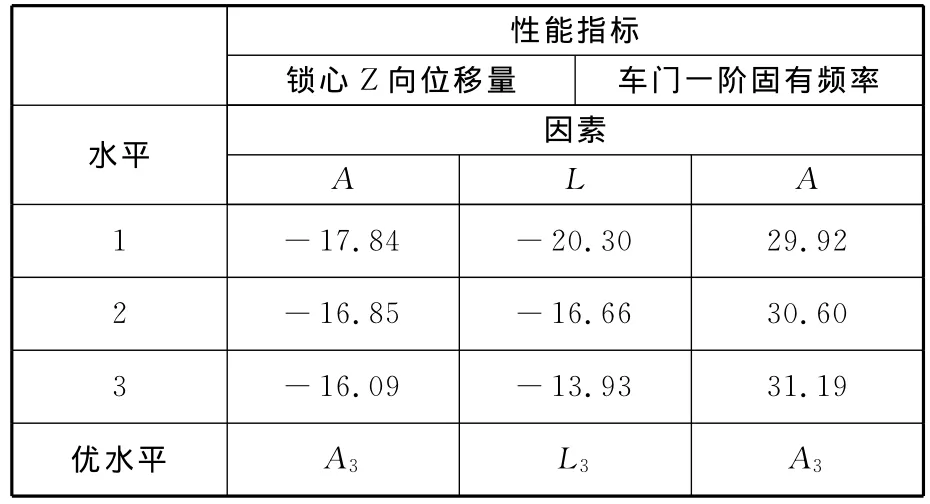
表9 显著因素优水平判断
由表9可知,不管是锁心Z向位移量,还是车门一阶固有频率,A3都是优水平。锁心Z向位移量的另一个优水平为L3。
车门的重量也是设计过程中必须考虑的因素,它与车门的制造成本密切相关。在满足车门结构性能的前提下,车门重量应越轻越好。从轻量化设计考虑,对非显著因素都取下限值,即第一水平,则得到的最佳组合为A3B1C1D1K1L3M1。即车门内板厚度为1.0mm;车门外板厚度为0.7mm;腰带梁板厚度为0.7mm;窗框厚度为0.8mm;门锁安装板厚度为0.8m;铰链安装板厚度为2.0mm;铰链加强板厚度为1.4mm。
按照最佳组合中的因素水平进行有限元分析,经车门下垂刚度分析得到的锁心Z向位移量为4.66mm;经车门上扭刚度分析得到的车门上部最大位移为5.94mm;经车门下扭刚度分析得到的车门下部最大位移为7.23mm;车门一阶固有频率为36.22Hz。优化后的车门结构性能指标均满足设计要求。车门重量的改变为Δm=-0.2kg,与原车门结构相比,车门重量减轻了。
初始的设计组合为A2B2C2D2K2L2M2,由表5中的ηX值可计算得到锁心Z方向的位移增益为

由表6中的ηD值可计算得到车门的一阶固有频率增益为

上述增益并不是通过更换车门材料或者采用其他方式获得的,而是参数设计的结果。由于参数组合选得好,所以车门结构性能的稳健性有了一定的提高。
3 结语
本文运用Taguchi方法中的参数设计法进行车门结构稳健性优化,找出了对车门下垂刚度和一阶固有频率影响最大的车门板件。在保证车门结构性能满足设计要求的前提下,通过合理的车门板件厚度组合,提高了车门结构性能的稳健性,减轻了车门的重量,为汽车车身结构的稳健设计和车身的轻量化设计提供了可资借鉴的经验,具有较强的工程实用性。
[1]万德安,赵建才.轿车车门刚度有限元分析及结构优化[J].汽车工程,2001,23(6):385-388.
Wan Dean,Zhao Jiancai.The FEA and Structural Optimization for Car Doors[J].Automotive Engineering,2001,23(6):385-388.
[2]王宏雁,徐少英.车门的轻量化设计[J].汽车工程,2004,26(3):349-353.
Wang Hongyan,Xu Shaoying.A Study on Lightweight Design of Car Door[J].Automotive Engineering,2004,26(3):349-353.
[3]Shin J K,Lee K H,Song S I,et al.Automotive Door Design with the ULSAB Concept Using Structural Optimization[J].Structural and Multidisciplinary Optimization,2002,23(4):320-327.
[4]Maglaras G,Ponslet E,Haftka R T,et al.Analytical and Experimental Comparison of Probabilistic and Deterministic Optimization[J].AIAA Journal,1996,34(7):1512-1518.
[5]黄金陵,崔岸,陈晓华,等.稳健设计方法用于车门系统设计[J].汽车工程,2006,28(11):1011-1014.
Huang Jinling,Cui An,Chen Xiaohua,et al.Robust Design of Automotive Door System[J].Automotive Engineering,2006,28(11):1011-1014.
[6]李超,钟志华.Taguchi设计方法和有限元分析方法在车门系统设计中的应用[J].机械科学与技术,2010,29(9):1168-1171.
Li Chao,Zhong Zhihua.Application of Taguchi's Approach and Finite Element Method to the Design of a Door System[J].Mechanical Science and Technology for Aerospace Engineering,2010,29(9):1168-1171.
[7]Koch P N,Yang R J,Gu Wei.Design for Six Sigma Through Robust Optimization[J].Structural and Multidisciplinary Optimization,2004,26:235-248.
[8]Zhu P,Zhang Y,Chen G L.Metamodel based Lightweight Design of an Automotive Front Body Structure Using Robust Optimization[J].Proceedings of the Institution of Mechanical Engineers,Part D:Journal of Automobile Engineering,2009,223(9):1133-1147.
[9]Sun Guangyong,Li Guangyao,Zhou Shiwei,et al.Crashworthiness Design of Vehicle by Using Multiobjective Robust Optimization[J].Structural and Multidisciplinary Optimization,2011,44:99-110.
[10]黄石华,成爱国,胡朝辉,等.基于6σ稳健性的拼焊板车门轻量化研究[J].汽车工程,2011,33(3):262-266.
Huang Shihua,Chen Aiguo,Hu Zhaohui,et al.A Research on the Lightweighting of TWB Door Based on Six Sigma Robustness[J].Automotive Engineering,2011,33(3):262-266.
[11]Taguchi G.Introduction to Quality Engineering:Designing Quality into Products and Processes[M].Tokyo:Asian Productivity Organization,1986.
[12]任露泉.试验设计及其优化[M].北京:科学出版社,2009.
[13]张建方.外表设计及其案例研究(Ⅰ)[J].数理统计与管理,1996,25(1):43-52.
Zhang Jianfang.Exterior Design and Case Studies(Ⅰ)[J].Mathematical Statistics and Management,1996,25(1):43-52.
