星地双基合成孔径雷达聚束模式快速BP算法

张文彬*①② 邓云凯① 王 宇①



星地双基合成孔径雷达聚束模式快速BP算法

张文彬邓云凯王 宇

(中国科学院电子学研究所 北京 100190)(中国科学院大学 北京 100049)

该文提出了一种应用于双基合成孔径雷达聚束模式的快速反向投影(FBP)算法，该算法在距离向压缩上使用地面接收器的同步信道作为回波信号的距离向匹配滤波器，在方位向压缩上采用2次相位校正降低快速BP算法中的近似误差对成像造成的影响，算法的计算复杂度为。最后利用仿真数据和实测数据在图形处理器(GPU)上对该算法进行了验证。

双基合成孔径雷达(Bi-SAR)；快速反投影(FBP)算法；计算复杂度；图形处理单元(GPU)

1 引言

近十几年，双基合成孔径雷达(Bistatic Synthetic Aperture Radar, Bi-SAR)已经成为了合成孔径雷达信号处理领域的一个研究热点，出现了很多的成像算法。在双基合成孔径雷达图像中，相位是非常重要的，尤其是在双基干涉合成孔径雷达(Bi-InSAR)和双基Tomography SAR中。在可行的Bi-SAR成像算法中，反向投影(BackProjection, BP)算法可以获得高精度的相位信息，但该算法的计算复杂度远大于频域算法的计算复杂度。为了降低BP算法的计算复杂度，很多文献提出了快速BP算法。到目前为止，快速BP算法主要有两种，它们的计算复杂度分别为和。尽管后一种算法的计算速度快于前者，但是前者使用了更少的同步操作，更方便应用在并行计算当中。算法需要从距离向压缩后的数据到最终的成像结果，需要次迭代。每次迭代的结果都要最为下一次迭代的输入值，因此必须在上一次迭代结束后才能开始下一次迭代。对于核数众多的GPU编程实现，各个GPU核要在每次迭代时进行一次同步操作以保证各个GPU核都完成本次迭代操作。这种同步操作在多GPU开发时是极其困难的。同时在多核GPU程序开发时的另一个问题是负载平衡，由于迭代次数众多，单次迭代运算量较少，因此负载平衡将成为一个极难优化的问题。如果负载不能很好的被平衡，则最终的运行时间将受限于最差的运行单元。算法的另外一个问题是数据输出问题。每次迭代数据都要在CPU的内存和GPU的显存中输出一次，算法需要大量的迭代操作因此需要大量的数据传输，同时每次迭代运算相对较少，因此传输时间将大大降低GPU的并行效果。而的算法仅有一次迭代，并且每次迭代的运算相对算法多，因此上述的同步问题和负载平衡优化问题都被简化。同时随着迭代次数的减少，数据传输也被大大降低，因此大大提高的GPU的并行效果。

文献[5-11]中涉及到的所有的双基Fast Back- Projection (FBP)算法在进行距离向压缩时，每条距离线上都会使用相同的线性调频信号来作为匹配滤波器。而在本文所提出的FBP算法中，我们使用同步接收机接收到的信号进行距离向回波信号的压缩。该算法有以下的优点：首先，在方位向处理过程的第2步中，快速BP算法使用近似的距离来取代精确的距离。近似距离和精确距离之间的差异所引起的误差，我们称之为FBP逼近误差。回波的距离徙动越大，随之带来的误差影响也就越大。由于包含在同步信号中的成像几何信息可以减少回波的距离徙动，所以本文提出的方法可以减少的FBP算法的逼近误差。其次，BP算法是基于成像几何的相干累加，所以卫星轨道的测量误差会给成像结果带来显著的影响。由于同步信号中的几何测量误差可以减少在回波信号中几何测量误差，所以本文提出的方法可以降低成像指标对轨道测量精度的要求。第三，由于双基模型中发射器和接收器位于不同的平台，它需要时间和相位同步，否则会对成像结果产生很大影响。该方法中用到的同步信号中的同步信息减少了额外的时间和相位的同步操作。第四，当线性调频信号在通过大气层时，由于噪声和衰减的影响，当它到达同步通道时，线性调频信号的幅度发生了变化。所以，起初的多个线性调频脉冲信号数据可能会因此丢失。由于同步接收机和回波接收机的起始采样时间是相同的，所以本文所提出的方法可以减弱这种影响。文献[5-11]没有明确分析FBP逼近误差对幅度和相位误差的影响，本文则对这些影响进行了分析，从中可以看到，该算法采用的2次相位校正，可以进一步减小FBP逼近误差所造成的影响，从而获得更高质量的图像。

本文结构安排如下：在第2节中提出了基于双基SAR的FBP算法；在第3节中，分析了所提出算法的计算复杂度和2次相位校正的优点；在第4节，使用仿真和实测数据来验证其正确性。

2 双基快速BP算法

2.1 双基合成孔径雷达系统简介

Bi-SAR系统包含1个发射机子系统和1个接收机子系统。发射机子系统固定在卫星上，这和单基星载SAR系统的发射机子系统是一样的。而与单基星载SAR系统不同的是，接收机子系统是固定在地面上的。为了获得足够大的场景，接收器子系统安置在现场附近的一座小山的山顶上，该接收器子系统包含同步接收机和回波接收机。Bi-SAR配置的几何构形如图1所示。

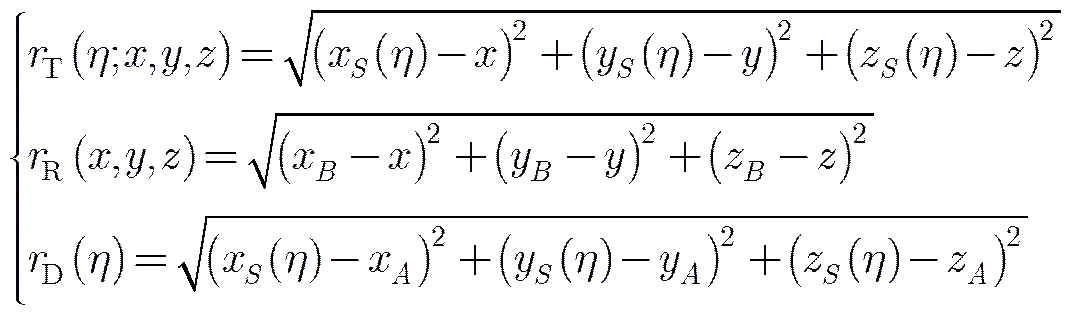
同步接收机的作用是同步发射子系统和接收子系统的时间和相位。图1中，同步接收机的天线指向卫星，并且直接从卫星接收线性调频信号；回波接收机的天线指向成像场景，用来接收从场景返回的回波。同步接收机和回波接收机使用相同的振荡器来合成混频信号，并使用具有相同时钟的ADC(模数转换器)来对混频后的同步信号和回波信号进行采样。所以同步接收机和回波接收机的采样几乎可以同时忽略振荡器的噪声。图2中为接收机子系统流程图。

对于所采用的系统的每个脉冲重复周期的工作方式如下：卫星发送线性调频脉冲信号，当同步通道接收了线性调频脉冲信号，它会记录线性调频脉冲信号并且同时触发回波通道记录回波信号。除非同步通道接收了下一次的线性调频脉冲信号，否则同步信道和回波信号会一直记录之前的信号。

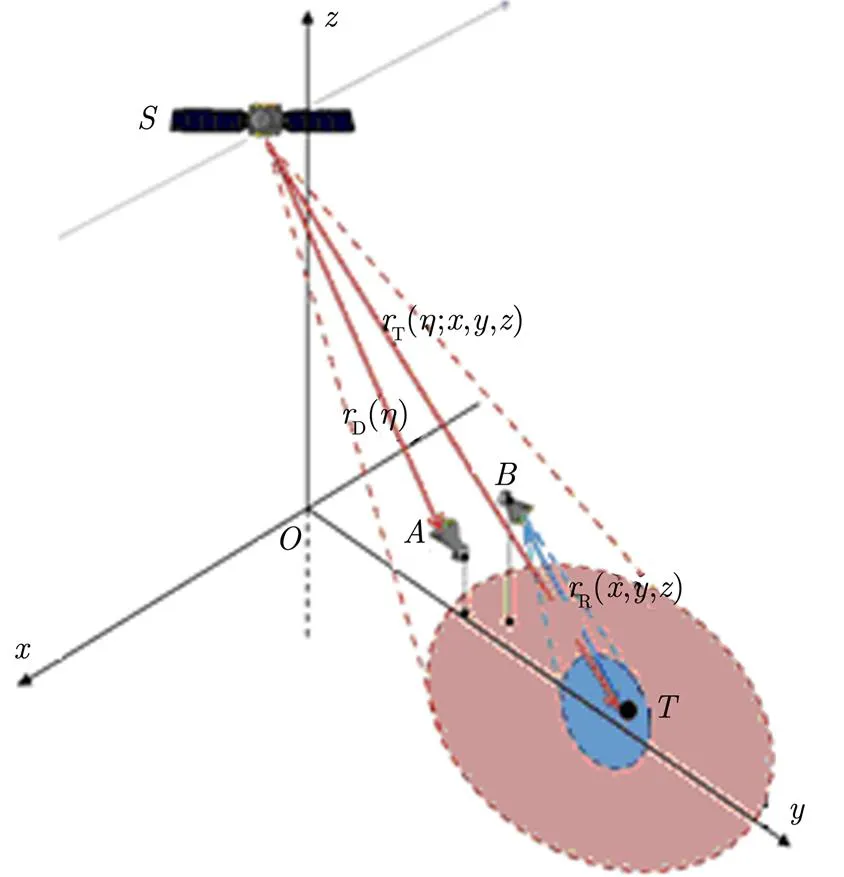
图1 Bi-SAR配置的几何构形

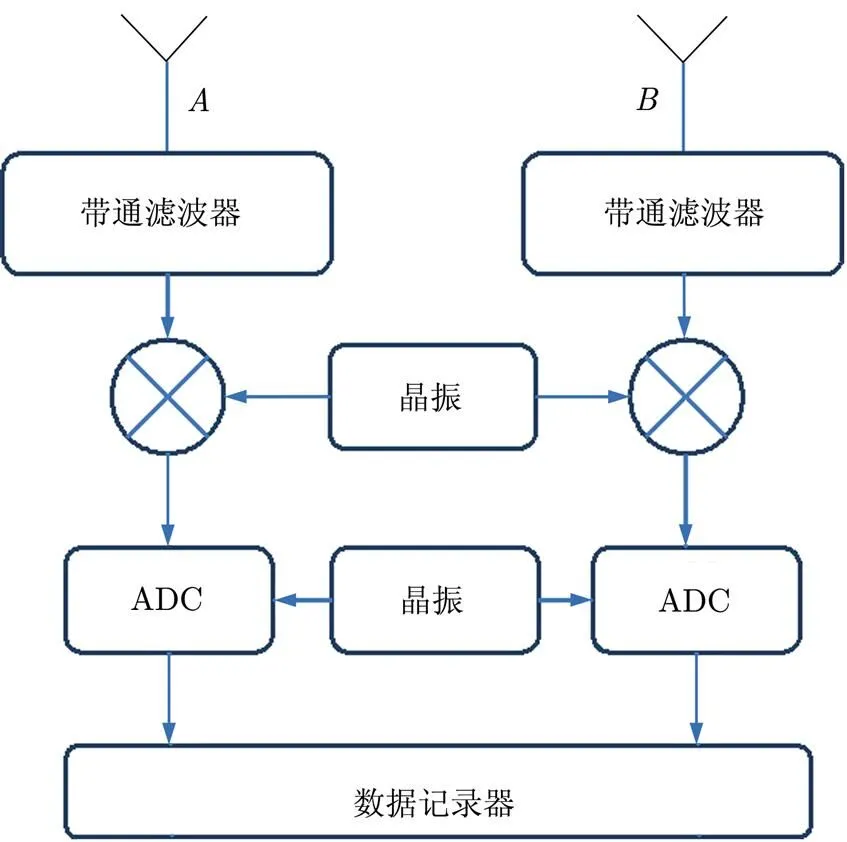
图2 接收机子系统流程图

2.2 快速BP算法的理论分析

图3为所提出的快速BP算法的流程图。所提出的算法分为3步：距离压缩，子图像处理和最终图像处理。每一幅子图像都是最终图像的1个低分辨率副本，它们覆盖了相同的成像区域。图4(a)为最终图像的成像网格，图4(b)为子图像的成像网格。在图4(a)中所有的点表示了最终图像的成像位置，图4(b)中的红色的点表示了子图像的成像位置。

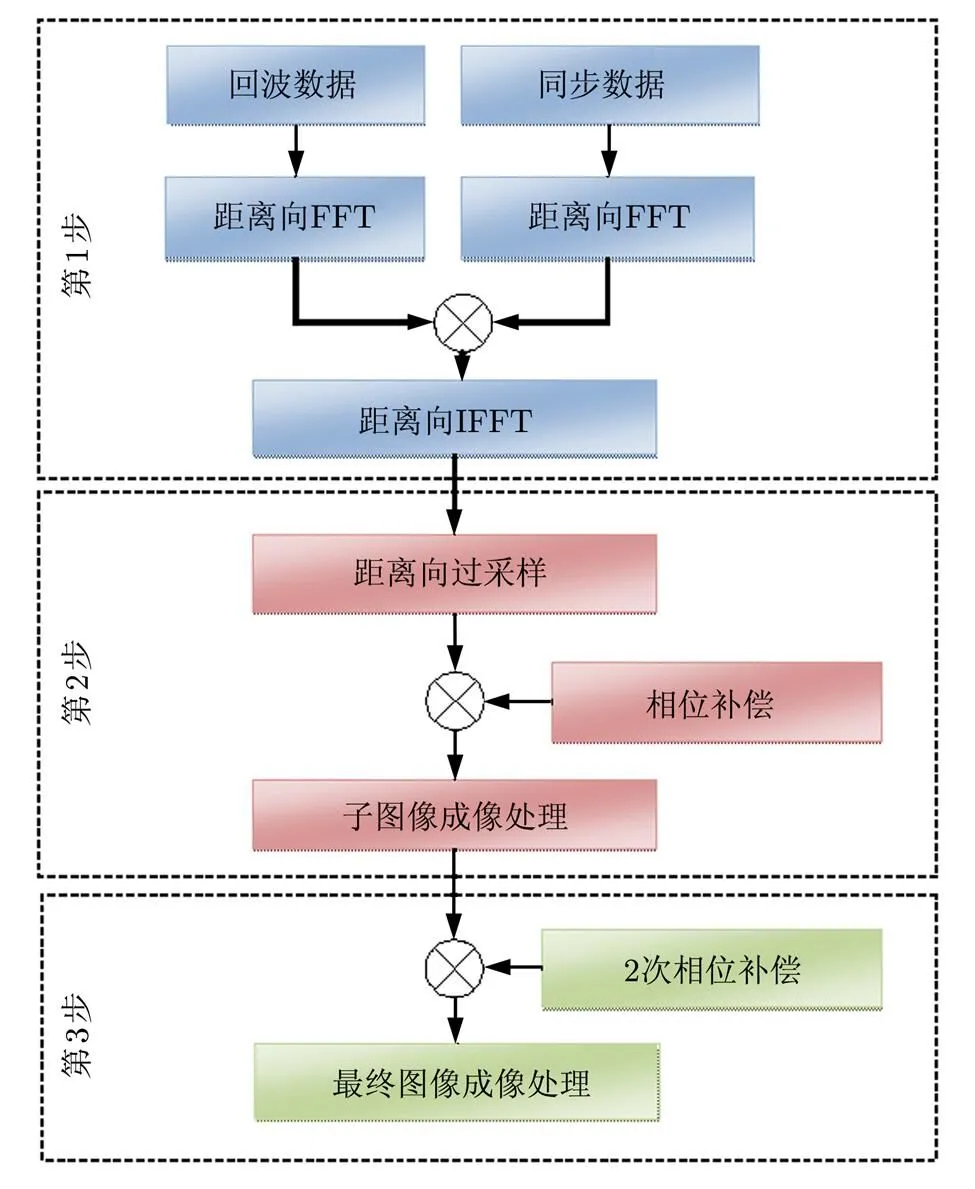
图3 快速BP算法的流程图

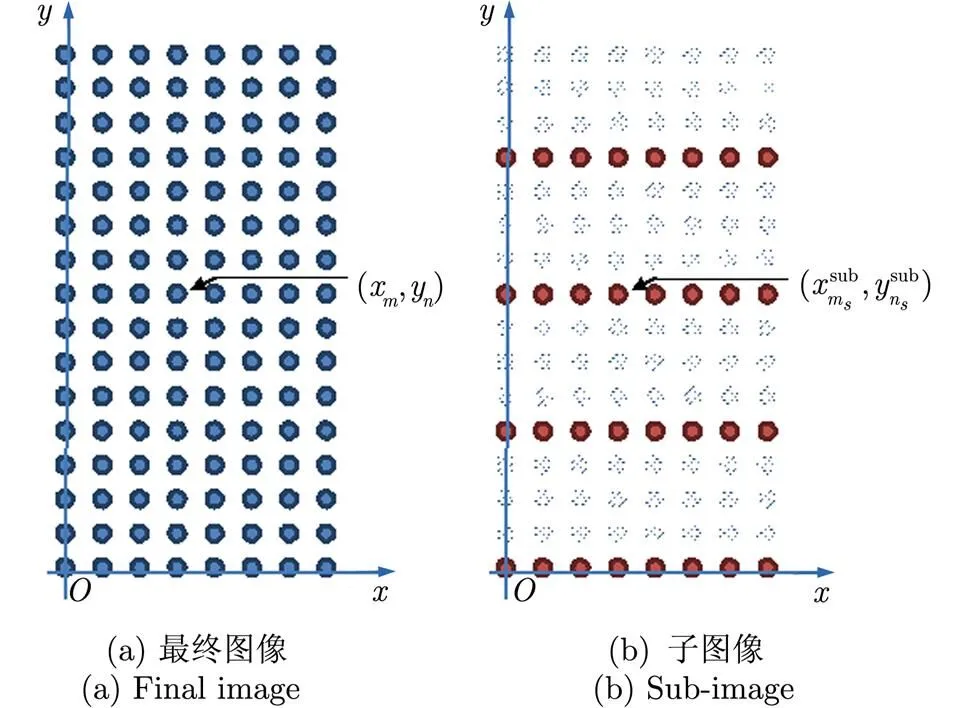
图4 最终图像和子图像的成像网格的关系

为了提高计算效率，我们可以先获得子图像序列，然后使用子图像序列获得最终的图像。文献[12]给出了这些原则并且介绍了单基合成孔径雷达的相应算法。相比起单基的快速BP算法，本文所提出的算法有以下3点改进。首先，单基合成孔径雷达和双基合成孔径雷达成像几何是不相同的，尤其是当双基合成孔径雷达的发射器和接收器不在同一平台上的时候。为了满足双基的几何模型，我们的算法中对成像几何模型进行了修正。其次，为增强成像的质量，我们的算法使用同步通道记录的线性调频信号作为距离向压缩处理过程中的匹配滤波器，并且加入了2次相位校正。这两项改进可以减少由于快速BP近似引起的误差。不仅如此，前一项改进也可以降低对卫星轨道精度的要求。第三，我们给出了大合成孔径的处理方法。假设距离线的数量为，每条距离线上的采样点数为，合成孔径的长度为，要求最终图像的大小为，距离压缩之后的数据沿着方位向被分成个数据块，每个数据块的大小为,和分别为方位向和距离向的过采样率。也就是说，如果最终图像的网格是(x,y)，那么子图像的网格是。

步骤1 距离向压缩 使用同步接收机接收的线性调频信号作为距离向压缩的匹配滤波器。在距离向压缩后为：

(4)

(5)

距离压缩后，传统的BP的方法的处理过程如下：

首先，频域补零对每一条距离线进行过采样，这里用到了傅里叶变换中频域补零相当于时域插值的性质。

由于采用直达波进行匹配时与常规处理的不同，BP的相位补偿要根据式(5)计算。过采样之后传统BP算法的方位向可以表示为：

(7)

本文提出的快速BP算法的方位向压缩分为步骤2和步骤3。

步骤2 获得子图像序列 每个子图像采用传统的BP算法进行成像。以第个子图像为例，基于式(6)，子图像的方位向可以使用下面的公式进行聚焦，

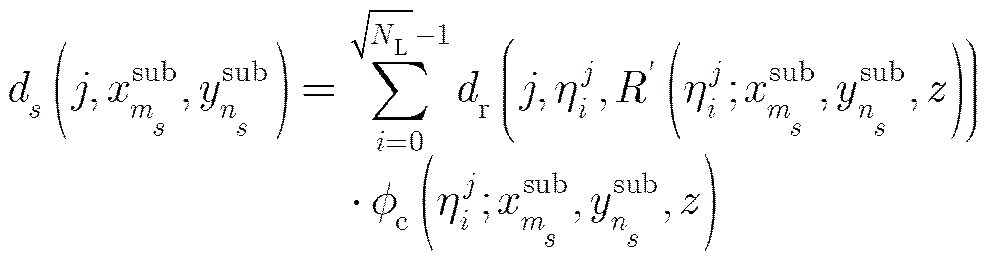
步骤3 获得最终的图像 使用之前获得的一系列子图像来获得最终的图像。在图4(b)中，每个子图像只需要计算红点处的值，而最终的图像需要计算所有的点是图4(a)中的点。蓝点处的值是这样计算的：选择每幅子图像中离它最近红点，然后计算这些红点2次相位校正(式(14)中给出)后的成像值的和。也就是说，为了计算最终图像中处的值，我们在每幅子图像中找到和它近似的位置，将这些位置的点在2次相位校正之后相加作为最终图像处的值。其中寻找位置是如下表述的一个最优化问题：

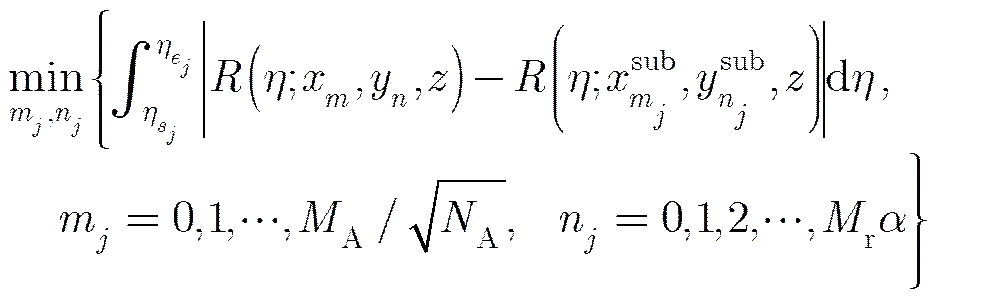
(10)

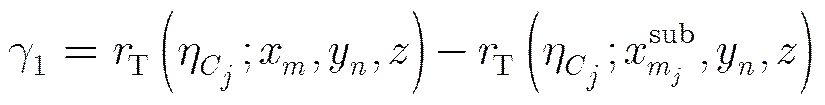
(12)

(13)

最终图像方位向聚焦公式为：

(15)

3 性能分析

3.1 计算复杂度

3.2 2次相位校正的必要性

快速BP算法在方位向处理的第2步中使用近似距离代替精确距离。近似距离和精确距离之间的差异是在几厘米的数量级上，比起距离向通常大于1 m的分辨率，这个误差是非常小的。但是对比波长来说，尤其X波段的波长也是在厘米数量级的，这个误差是无法忍受的，因此采用近似距离对于幅度的影响比较小，而对相位的影响比较严重。因为BP算法基于相干累加，所以相位误差会显著地影响快速BP算法的结果。近似距离和精确距离之间的差异的另一个特性就是在每个子块中，它接近于一个常值，所以我们可以通过使用2次相位校正来校正相位，以减少近似过程给相位带来的误差。

图5(a)和图5(b)分别是进行了2次相位校正和没有进行2次相位校正的结果。通过对比，能够看出2次相位校正还是非常有效率的。

3.3 采用同步信号作为距离向匹配滤波器的优势

采用同步接收机接收到的信号作为本算法距离向压缩时的匹配滤波器有3点优势：其一是可以减少快速BP算法的近似误差；其二是也可以降低卫星轨道测量精度的要求；其三是减少同步操作。

图5 有2次相位和没有2次相位校正结果比较

(1) 减少快速BP算法的近似误差

在方位向处理过程的第2步中，快速BP算法使用近似的距离来取代精确的距离。近似距离和精确距离之间的差异所引起的误差，我们称之为FBP逼近误差。回波的距离徙动越大，随之带来的误差影响也就越大。由于包含在同步信号中的成像几何信息可以减少回波的距离徙动，所以本文提出的方法可以减少FBP算法的逼近误差。

(2) 降低卫星轨道测量精度的要求

BP算法是基于成像几何的相干累加，所以卫星轨道的测量误差会给成像结果带来显著的影响。轨道参数在回波数据的斜距和同步数据的斜距中符号相反，同步信号中的几何测量误差可以抵消一部分在回波信号中几何测量误差，因此本文提出的方法可以降低成像指标对轨道测量精度的要求。

(3) 减少同步操作

首先，由于双基模型中发射器和接收器位于不同的平台，它需要时间和相位同步，否则会对成像结果产生很大影响。该方法中用到的同步信号中的同步信息减少了额外的时间和相位的同步操作。其次，当线性调频信号在通过大气层时，由于噪声和衰减的影响，当它到达同步通道时，线性调频信号的幅度发生了变化。所以，起初的多个线性调频脉冲信号数据可能会因此丢失。由于同步接收机和回波接收机的起始采样时间是相同的，所以本文所提出的方法可以减弱这种影响。

4 仿真和实测数据实验

在这一节中，我们使用了仿真数据和实测数据来验证所提出的算法，该算法使用GPU进行并行加速。仿真参数列在表1中。

表1仿真双基合成孔径雷达参数

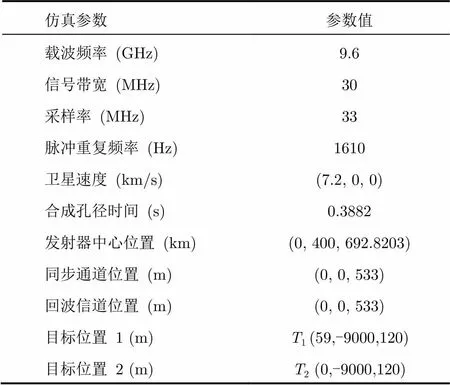
Tab. 1 Parameters of Bi-SAR simulation

图6(a)展示了普通BP算法的处理结果，图6(b)展示了快速BP算法的处理结果，其中距离向的过采样率和方位向的过采样率都是1。从比较中，我们可以发现使用快速BP算法得到的结果与使用普通BP算法得到的结果非常相似。红线是子图像序列成像网格。目标靠近子图像序列成像网格，目标离得比较远。

图7(a)使用快速BP算法展示了目标的脉冲响应。在图8中，蓝线代表普通BP算法的包络，红线代表快速BP算法的包络。从比较之中，我们可以发现快速BP算法的结果与普通BP算法的结果非常相似。点目标的脉冲响应展示在图7(b)和图9中。从这些图中，我们可以得出这样的结论：快速BP算法的结果和反投影(BP)算法的结果是非常相似的。

实测参数列在表2中。

表2 实验双基合成孔径雷达参数[4]

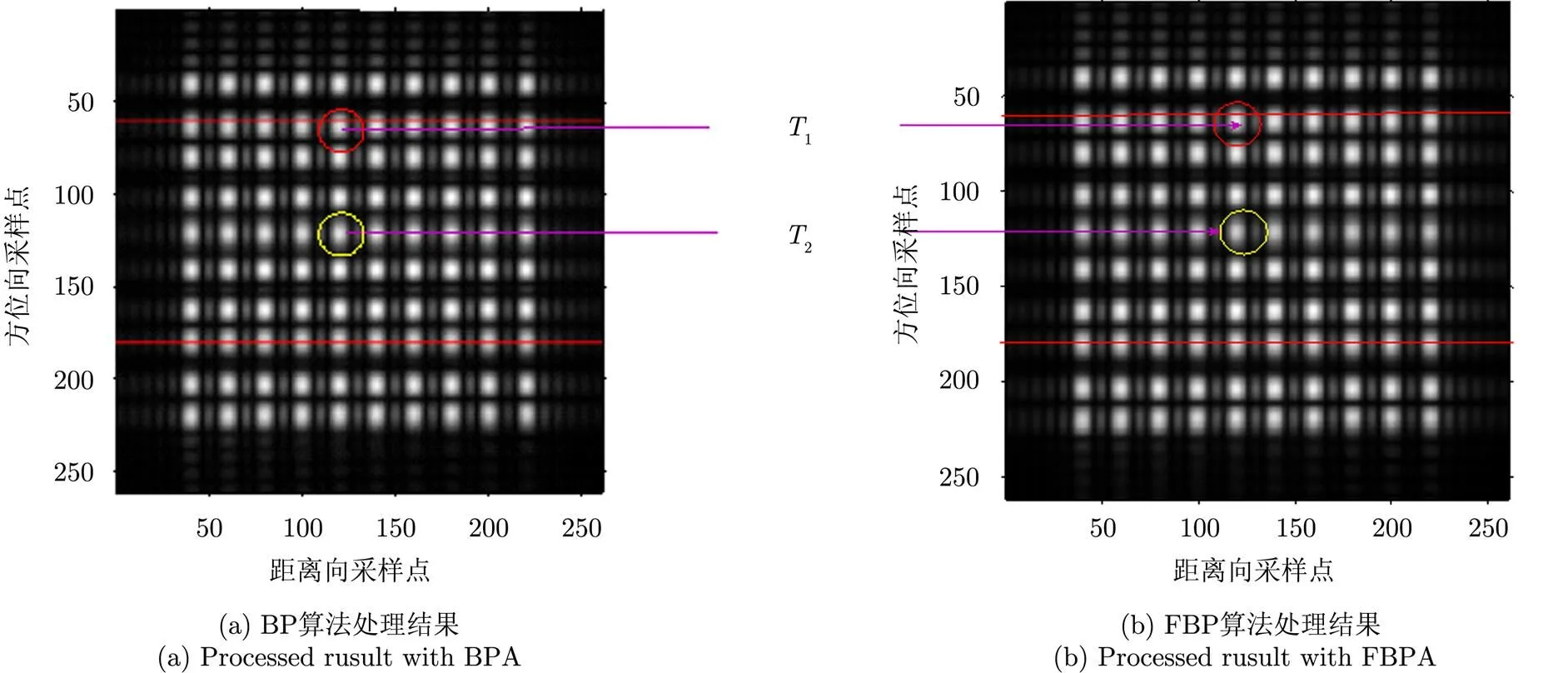
Fig. 6 BP算法和FBP算法处理结果比较

图7 目标T1和目标T2的脉冲响应(FBP)

图8目标1的FBP和BP算法结果对比

图9目标2的FBP和BP算法结果对比

TerraSAR-X工作在X波段，其波长要比L波段的合成孔径雷达的波长短。在近似距离与精确距离之差相同的情况下，波长越短，快速BP算法的近似误差就越严重。所以为了获得比较高的图像质量，X波段合成孔径雷达需要更加精准的相位信息。从图10(b)中可以看出我们的快速BP算法的处理结果和图10(a)中的普通BP算法的处理结果是非常相似的。图11(a)是场景中心处成像后的1条距离线上各点的对比结果，图11(b)是同一距离门上各点的对比结果。可以看出两者的残差很小。表3显示了在GPU(NVIDIA Tesla C2050)上的反投影和快速反投影算法的处理时间，由于并行优化问题，实际速度慢于理论值，但它仍然要比传统的BP算法快20倍的速度。通过对比，可以看出FBP算法要比传统的BP算法快很多。所以无论是从仿真数据的结果还是实测数据的结果，都可以得出结论：我们所提出的算法是稳定的。

图10 BP算法和FBP算法处理的TerraSAR-X

图11 典型位置的聚焦结果

表3处理时间的比较

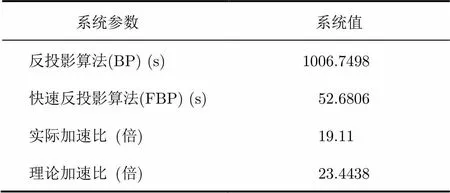
Tab. 3 Comparison of process time

5 总结

本文提出了一种用于处理双基合成孔径雷达数据的快速BP算法。使用同步接收机接收的信号作为距离向压缩的匹配滤波器，既可以减少快速BP算法的近似误差，也可以降低卫星轨道测量精度的要求。进行2次相位校正的目的是为了减少由近似引起的相位误差，达到更好的效果。仿真数据和实测数据的成像结果证明该算法可以以更少的计算复杂度获得与传统BP算法非常相近的图像质量。

附录A

假设卫星沿轴运动的平均速度是，则卫星的位置为，根据式(5)有

(A-2)

(A-4)

因此式(A-2)近似为

将式(A-5)带入式(9)得：

(A-6)

由于式(A-6)的解析表达式很难求解，因此求解式(A-6)得简化式(A-7)：

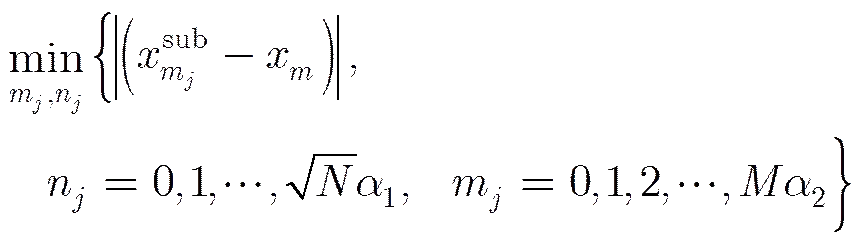
有

(A-8)

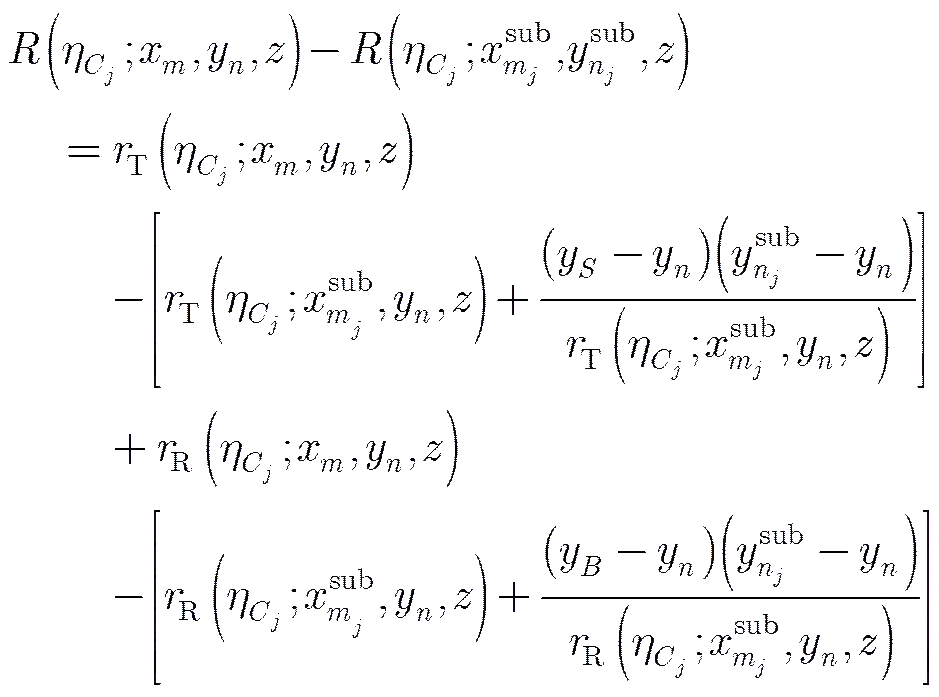
(A-10)

有：

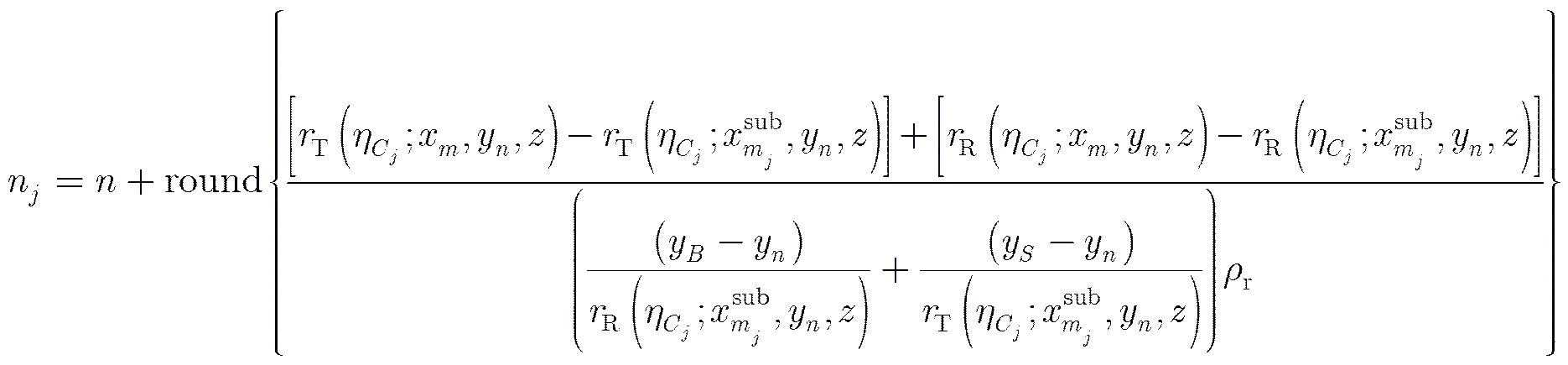
(A-12)

[1] Dai C, Zhang X, and Shi J. Range cell migration correction for bistatic SAR image formation[J]., 2012, 9(1): 124-128.

[2] Wong F H, Cumming I G, and Neo Y L. Focusing bistatic SAR data using the nonlinear chirp scaling algorithm[J]., 2008, 46(9): 2493-2505.

[3] Zhang W,Tong C, Zhang Q,.. Extraction of vibrating with dual-channel fixed-receiver bistatic SAR[J]., 2012, 9(3): 507-511.

[4] Wang R, Deng Y K, Loffeld O,.. Processing the azimuth-variant bistatic SAR data by using monostatic imaging algorithms based on two-dimensional principle of stationary phase[J]., 2011, 49(10): 3504-3520.

[5] Ulander L MH, Hellsten H, and Stenstrom G. Synthetic- aperture radar processing using fast factorized back- projection[J].ems, 2003, 39(3): 760-776.

[6] Ding Y and D. C. Jr. Munson. A fast back-projection algorithm for bistatic SAR imaging[C]. IEEE ICIP, Oct. 2002: II-449-II-452.

[7] Frölind P P and Ulander L M H. Evaluation of angular interpolation kernels in fast back-projection SAR processing[J].,, 2006, 153(3): 243-249.

[8] Chen J, Xiong J, Huang Y,.. Research on anovel fast backprojection algorithm for stripmap bistatic SAR imaging[C]. Synthetic Aperture Radar (APSAR), 2007 1st Asian and Pacific Conference on Huangshan, Nov. 5-9, 2007: 622-625.

[9] Cassola M R, Prats P, Krieger G,.. Efficient time- domain focusing for general bistatic SAR configurations: bistatic fast factorised backprojection[C]. Synthetic Aperture Radar (EUSAR), 2010 8th European Conference on Aachen, Germany, June 2010.

[10] Liu M, Li C, and Shi X. A back-projection fast autofocus algorithm based on minimum entropy for SAR imaging[C].Synthetic Aperture Radar (APSAR), 2011 3rd International Asia-Pacific Conference on Seoul, Korea (South), Sept. 2010: 1-4.

[11] Ponce O, Prats P, Rodriguez-Cassola M,.. Processing of circular SAR trajactories with fast factorized back- projection[C]. IEEE Geoscience and Remote Sensing Symposium (IGARSS), 2011: 3692-3695.

[12] Yu H,Zhang Y, and Zhu L. UWB LFMCW radar imaging based on dechirp processing[J]., 2005, 27(7): 39-41.

[13] Zhang X, Shi J, and Zhe L. GPU-based parallel back projection algorithm for the translational variant BiSAR imaging[C]. Geoscience and Remote Sensing Symposium (IGARSS), 2011 IEEE International, Vancouver, BC, July 2011: 2841-2844.

A Fast Backprojection Algorithm for Spotlight Mode Bi-SAR Imaging

Zhang Wen-binDeng Yun-kaiWang Yu

(Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China)(University of Chinese Academy of Sciences, Beijing 100049, China)

A Fast BackProjection (FBP) algorithm for spotlight mode Bistatic Synthetic Aperture Radar (Bi-SAR) was presented. The sync channel signal from a land receiver was taken as the matched filter for the echo signal in the phase of range compression. The secondary phase calibration was shown to decrease the approximation error effects of FBPA in the phase of azimuth compression. Computational complexity of this algorithm was. In addition, this algorithm was validated on a Graphic Processing Unit (GPU) using measured and simulation data.

Bistatic Synthetic Aperture Radar (Bi-SAR); Fast BackProjection (FBP) algorithm; Computational complexity; Graphic Processing Unit (GPU)

TN957

A

2095-283X(2013)03-0357-10

10.3724/SP.J.1300.2013.13031

2013-03-25收到，2013-08-01改回；2013-08-19网络优先出版

中国科学院“百人计划”项目(6065-07)资助课题

张文彬 wbzhang@mail.ie.ac.cn

张文彬(1980-)，男，江苏南京人，博士生，研究方向为合成孔径雷达波束控制技术。

E-mail: wbzhang@mail.ie.ac.cn

邓云凯(1962-)，男，研究员，博士生导师，研究方向为星载合成孔径雷达系统设计。

王 宇(1980-)，男，研究员，博士生导师，研究方向为合成孔径雷达信号处理、双基SAR信号处理。