机载差分干涉SAR双轨法和三轨法的误差比较分析

李焱磊*①② 梁兴东① 丁赤飚①



机载差分干涉SAR双轨法和三轨法的误差比较分析

李焱磊梁兴东丁赤飚

(中国科学院电子学研究所 北京 100190)(中国科学院大学 北京 100049)

机载差分干涉SAR (D-InSAR)是一种极具潜力的地表形变监测技术，该文对该技术中经常使用的双轨法和三轨法两种工作模式的误差进行了比较分析。分析过程中根据互相独立的原则对各种误差进行分解和归类，并且考虑了运动误差与其它误差因素之间的耦合关系，在此基础上推导出两种工作模式下形变测量误差的解析表达式。结果表明：当运动误差幅度较小的时候，三轨法可以降低对外部地形数据的要求，相对于双轨法，它的优势非常显著；当运动误差幅度较大的时候，三轨法需要使用高精度的地形数据，它相对于双轨法的优势就不再明显。

差分干涉；机载SAR；误差分析；双轨法；三轨法

1 引言

差分干涉SAR (D-InSAR)是一种理想的对连续区域进行高精度地表形变监测的技术，由于对平台控制精度的要求很高，该技术首先在星载平台上得以实现。星载差分干涉SAR可以对大范围区域进行长期观测，目前已经成为一种成熟的地表形变监测技术，然而，重访周期过长、飞行轨道固定、分辨率低是绝大部分星载差分干涉SAR的共同缺点。机载差分干涉SAR可以有效弥补这些不足，它具有高的空间分辨率、灵活的重访周期和飞行轨道，在涉及形变监测的各种领域都具有极为广阔的应用前景。由于机载平台在大气层内飞行，飞行控制精度不及星载平台，所以其实现难度大于星载差分干涉SAR技术。

国外先进机载差分干涉SAR的载机平台配备了高精度自动驾驶仪，可以实现在以预设航线为轴心、5 m为半径的管道内飞行，但是国内SAR系统的载机平台还难以达到这样高的飞行控制水平。差分干涉SAR有多种工作模式：双轨法、三轨法、四轨法和长时序处理方法，较低的飞行控制水平限制了需要多次飞行的长时序处理在机载差分干涉SAR中的应用，为了尽量减少飞行次数以降低数据采集的难度，我们主要考虑双轨法和三轨法。

前人对机载差分干涉SAR的误差分析工作主要集中在三轨法的工作模式下，其主要原因在于三轨法对外部地形数据精度的要求比双轨法的要求低。不过这些工作没有充分考虑运动误差的影响，在大幅运动误差条件下三轨法比双轨法是否依然具有明显的优势有待商榷。本文对机载差分干涉SAR在双轨法和三轨法工作模式下的误差进行了系统的比较分析，分析过程中根据互相独立的原则对误差进行了分解和归类，并且考虑了运动误差与其它误差因素之间的耦合关系，从而明确了各种误差来源，通过敏感度分析确定了各种误差源对形变测量误差的贡献量。该工作可为机载差分干涉SAR工作模式的选择和系统指标的论证提供理论上的支撑。

在本文中出现了多个与运动误差相关的概念，为了避免混淆，先对它们进行如下说明：在SAR数据采集过程中，天线相位中心会偏离匀速直线运动轨迹，通过对实际轨迹进行拟合可以获得理想轨迹。运动误差是指天线相位中心的实际位置到目标的距离与其理想位置到目标的距离之差，它是可测量的，测量的误差称为残余运动。运动补偿处理并不能完全消除运动误差的影响，补偿之后残留的误差称为运动补偿误差。在运动补偿误差中，有一类误差是由于运动误差与斜距测量误差、飞行高度误差和地形误差等因素耦合造成的，此类误差称为耦合运动补偿误差。

为了便于比较分析，将双轨法和三轨法的数据获取几何画在同一幅图内，如图1所示：在与航迹垂直的切面上，,和表示天线相位中心的位置，其中与获取数据时间间隔较短，地表未发生形变，获取数据与前二者时间间隔较长，地表发生径向形变。双轨法使用和获取的复图像数据和外部地形数据；三轨法使用,和获取的复图像数据(为了提高测量精度，有时候也要利用外部地形数据)。

2 误差分析

2.1 双轨法的误差分析

双轨法的基本原理是：由地表形变发生前后的两幅SAR图像获得干涉图(包含地形和形变信息)，利用外部地形模拟出的干涉图去除其中的地形信息，从而获得形变信息。在图1中，由和获取的干涉相位(含地表形变信息)为

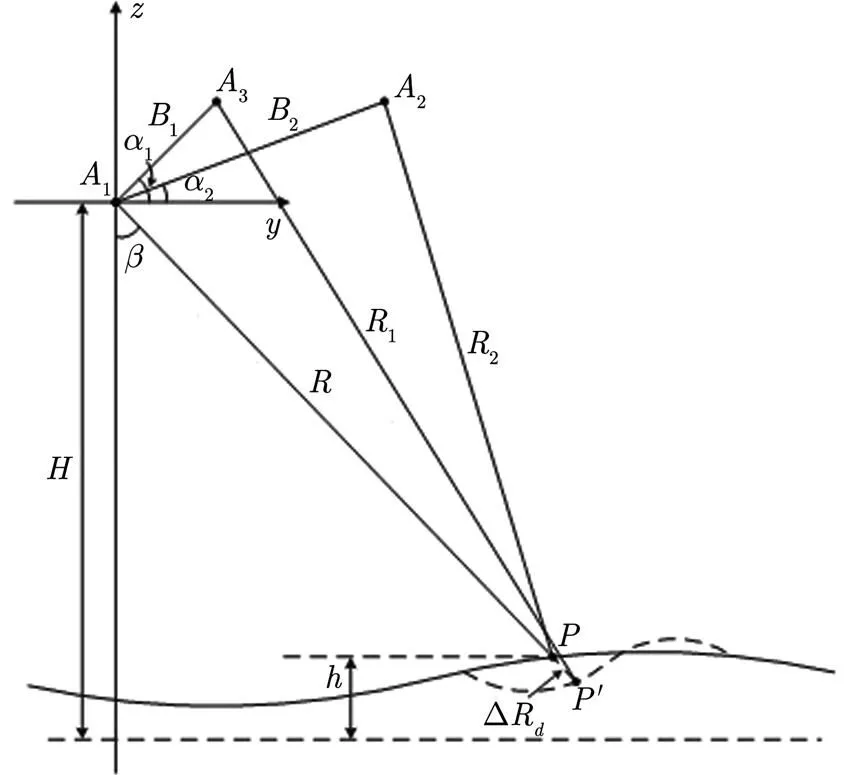
图1 差分干涉SAR数据获取几何

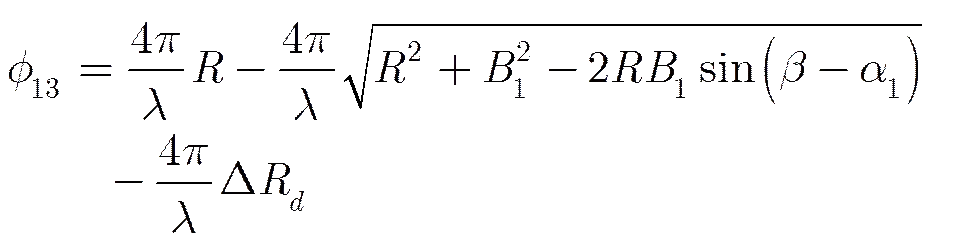
（2）

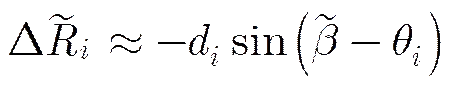
对其进行Taylor展开并取1阶近似，同时考虑运动误差与相位误差的比例关系，得

（4）

根据飞行轨道数据和外部地形数据计算出的模拟干涉相位(不含地表形变信息)为

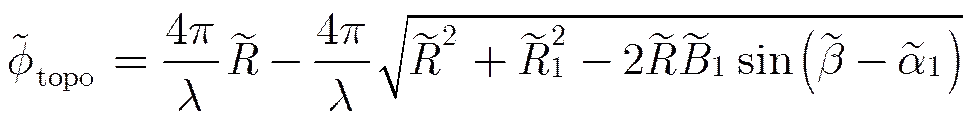
形变量的估计值为

(6)

差分干涉模式下的基线由两次飞行过程中天线相位中心的位置来决定(如图2所示)，假设和的测量位置分别为和，则

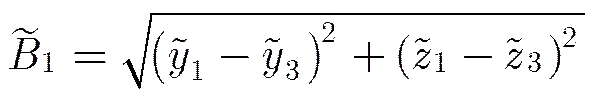
(8)

根据图1所示的几何关系，得

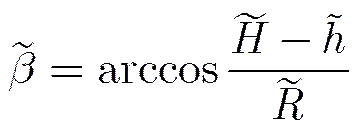
通过上述分析可知，双轨法形变测量过程中涉及的误差因素包括：去相关()、系统相位漂移(和)、大气延迟误差(和)、天线相位中心位置(,,,)、斜距()、飞行高度()和地形()，由于各种误差源互相独立，所以双轨法形变测量的均方误差为

(11)

由式(2)和式(6)得

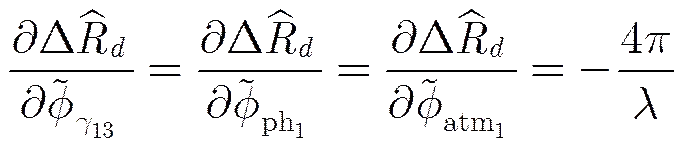
(13)

由式(6)、式(7)和式(8)得

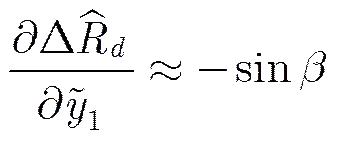
(15)

(16)

由式(2)、式(3)、式(4)、式(6)和式(9)得

（18）

（20）

将式(11)～式(20)代入式(10)，得

事实上，运动误差也具有随机特性。运动误差是实际轨迹与理想轨迹之差，理想轨迹的水平坐标()和竖直坐标()分别为实际轨迹水平坐标的均值和竖直坐标的均值，所以运动误差幅度的均值为0；由于实际轨迹可在理想轨迹周围的任意位置出现，所以可以假设运动误差的辐角服从上的均匀分布，设运动误差幅度的方差为，则

(22)

将式(22)代入式(21)，得

2.2 三轨法的误差分析

三轨法的基本原理是：由地表形变发生前后的两幅SAR图像获得干涉图1(包含地形和形变信息)，由地表形变发生前的两幅图像获得干涉图2(只包含地形信息)，将干涉图2中的地形相位从干涉图1的相位中去除，从而获得形变信息。在图1中，由和获取的干涉相位(不含地表形变信息)为

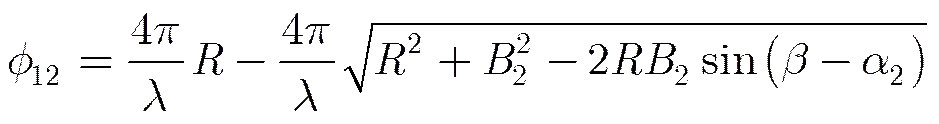
（25）

将式(24)所示的地形相位从式(1)中去除可以获得形变相位，在三轨法的实际操作过程中，为了提高估计精度先要对式(1)和式(24)进行去平地处理，为了进一步提高估计精度，可采用去地形处理，其中去地形的方法与双轨法中去地形的方法完全相同。不失一般性，这里对去地形的方法进行分析(实际上，平地可以视为一种低精度的地形数据)。地形相位如式(5)所示，经过去地形处理之后的干涉相位分别为

(27)

形变量的估计值为

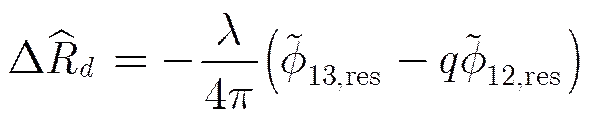
其中

(29)

与双轨法相比，三轨法由于多引入了一幅SAR图像数据，所以涉及的误差来源更多，具体包括：去相关(和)、系统相位漂移(,和)、大气延迟误差(,和)、天线相位中心位置(,,,,,)、斜距()、飞行高度()和地形()，由于各种误差源互相独立，所以三轨法形变测量的均方误差为

各种误差的敏感度分别为

(31)

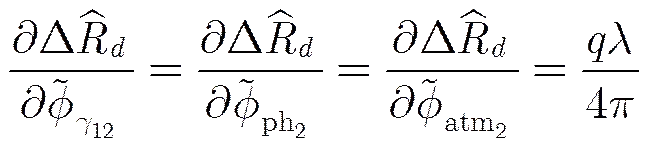
(33)

(34)

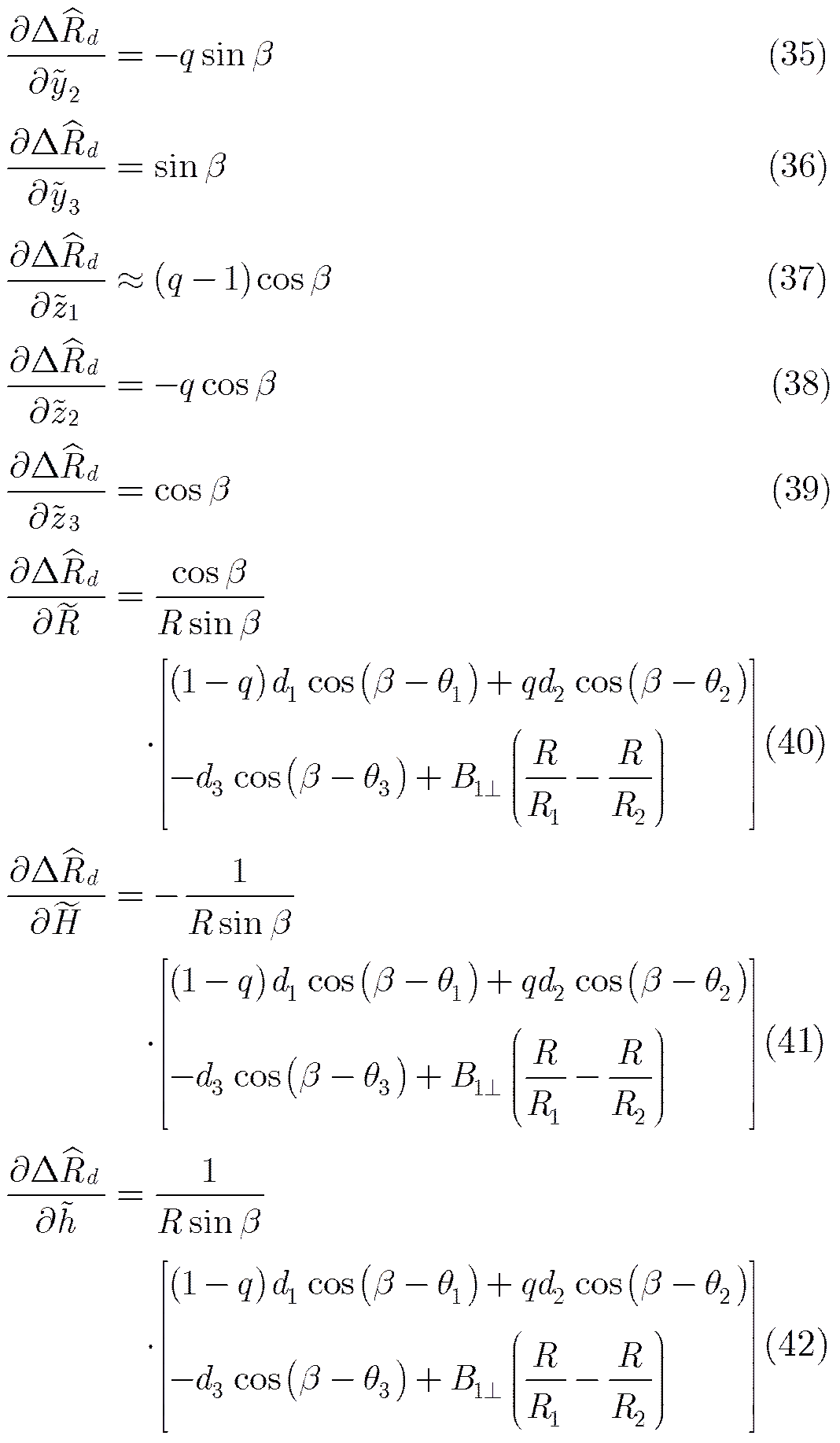
将各误差的敏感度和均方误差代入式(30)，并将运动误差的幅度和辐角也视为随机变量，通过化简，可得三轨法的形变测量的均方误差为

（43）

3 双轨法与三轨法的误差比较分析与仿真验证

由前面的分析可知，影响双轨法和三轨法地表形变测量精度的误差包括如下7种：去相关、系统相位漂移、大气延迟误差、残余运动(由天线相位中心位置决定)、斜距误差、飞行高度误差和地形误差。下面通过列表对两种工作模式下各种误差的贡献量进行比较分析(如表1所示)。

表1双轨法与三轨法各种误差贡献量的比较

Tab. 1 Comparison of the contributions of various errors in the two-pass and three-pass approaches

误差种类双轨法中的贡献量三轨法中的贡献量 去相关 系统相位漂移 大气延迟误差 残余运动 斜距误差 飞行高度误差 地形误差

取一组典型误差数值(如表2所示)，对上述理论分析结果进行Monte Carlo仿真验证。在仿真过程中，被分析的误差因素的取值范围如仿真结果的横坐标所示，其它误差因素均取表2所示的典型值；系统工作在P波段，波长为0.4835 m，下视角45°；由于误差的统计分布形式并不影响其均方误差的大小，所以这里任选了一种分布形式：高斯分布。

仿真结果如图3所示。

由于去相关因素在双轨法中的贡献量小于在三轨法中的贡献量，所以当相干系数很小的时候，双轨法的误差小于三轨法的误差，随着相干系数的提高，三轨法中去相关因素造成的误差迅速下降，三轨法的性能会超过双轨法的性能(见图3(a))。由于其它6种误差因素在双轨法中的贡献量大于在三轨法中的贡献量，所以在相同的条件下，不但双轨法的误差大于三轨法的误差，而且前者的增长速率大于后者的增长速率(见图3(b)～图3(g))。在实际中，相干性太差的情况应当予以避免，因此在相同的条件下，三轨法在性能上优于双轨法。

表2仿真中误差的典型值

Tab. 2 Typical values of the errors in the simulation

误差因素去相关系统相位漂移大气延迟误差残余运动斜距误差飞行高度误差地形误差 典型值(均方根)1.2°4 mm3 mm0.1 m0.1 m0.5 m

一般意义上来讲，三轨法的优势在于它对测量误差(尤其是地形数据误差)的容忍度较高，这一点已经从上面的分析和仿真中得以验证。但是，三轨法需要的SAR图像数据比双轨法多，而且当载机平台的飞行控制精度较低的时候，获取3幅满足要求的SAR图像往往需要重复飞行多次然后从中选取合适的数据，这样就会增加作业成本，如果三轨法的性能不能远高于双轨法的性能，在机载差分干涉SAR中选用三轨法就会失去意义。前面在仿真过程中，两种工作模式下各种误差的大小是相等的，为了进一步检验三轨法的性能是否远高于双轨法，需要增大三轨法中的测量误差，实际中获取高精度地形数据往往是困难的(要获取上面提到的0.5 m精度地形数据，需要为差分干涉SAR配备同机搭载的双天线干涉SAR系统)，所以可以选择地形误差作为检验的对象。在表1中，地形均方误差的系数中包含了基线和运动误差幅度的信息，在以往的分析过程中往往忽略了运动误差的影响，而运动误差恰恰是机载差分干涉SAR无法回避的问题。下面的仿真中，在不同的运动误差幅度下检验地形精度对两种工作模式形变测量精度的影响。

在图4(a)和图4(b)中，双轨法使用的地形数据精度均为0.5 m，在图4(a)中三轨法使用的地形数据精度也为0.5 m，在图4(b)中三轨法使用的地形数据精度为2.5 m。仿真结果表明，当地形数据精度从0.5 m恶化到2.5 m的时候，三轨法形变测量精度会随着运动误差幅度的增加而迅速恶化(见图4(b))

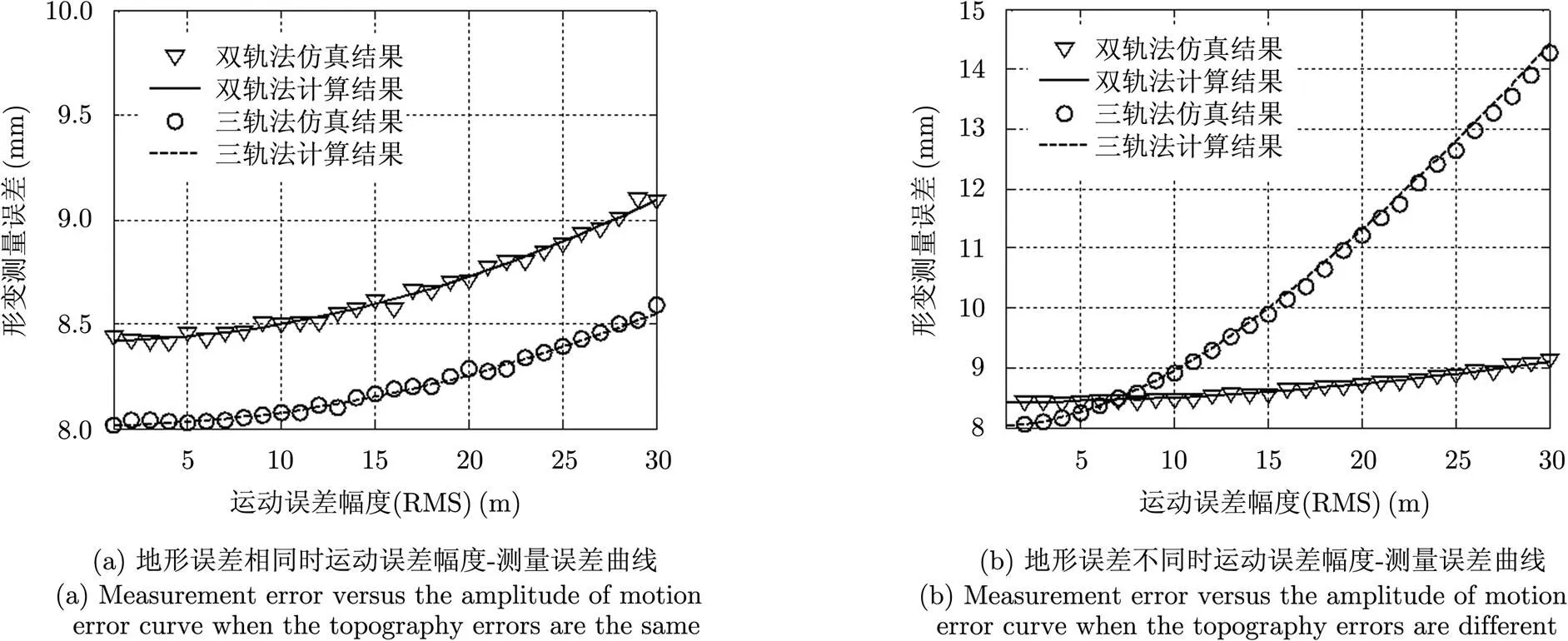
图4 不同地形精度下运动误差幅度对形变测量精度的影响

由此可见，三轨法的性能并不能“远高于”双轨法。2.5 m精度的地形数据仍然很难借助外部地形数据来获得(SRTM地形精度约为16 m)，因此，为差分干涉SAR配备同机搭载的双天线干涉SAR是必需的。

4 结论

本文从双轨法和三轨法的工作原理出发，对各种误差进行溯源分析并将其分为7种：去相关、系统相位漂移、大气延迟误差、残余运动、斜距误差、飞行高度误差和地形数据误差。通过分析得出两种工作模式下形变测量均方误差的表达式，与星载情况不同的是，机载差分干涉SAR需要考虑运动误差的影响。通过比较分析和仿真验证得出如下结论：在相同的情况下，三轨法在性能上优于双轨法；当运动误差幅度比较小的时候，三轨法可以降低对外部地形数据的要求，从而借助已有的地形数据(如SRTM地形数据)可以完成形变测量任务，而双轨法必须使用高精度地形数据，此时三轨法具有明显的优势；当运动误差幅度比较大的时候，运动误差与地形误差、斜距误差和飞行高度误差耦合造成的误差会相应增加，为了控制该误差，需使用高精度地形数据，因此无论使用三轨法还是使用双轨法，都必须为差分干涉SAR配备同机搭载的双天线干涉SAR，这时候三轨法相对于双轨法的优势并不明显。

[1] Massonnet D, Rossi M, Carmona C,.. Radar interferometric mapping of deformation in the year after the Landers earthquake[J]., 1994, 369: 138-142.

[2] Reigber A and Scheiber R. Airborne differential SAR interferometry: first results at L-band[J]., 2003, 41(6): 1516-1520.

[3] Jones C, Hensley S, and Michel T. Topography-dependent motion compensation: application to UAVSAR data[C]. IGARSS, 2009.

[4] Rosen P A, Hensley S, Wheeler K,.. UAVSAR: a new NASA airborne SAR system for science and technology research[C]. IEEE Conference on Radar, Verona, New York, Apr. 2006.

[5] 王超, 张红, 刘智. 星载合成孔径雷达干涉测量[M]. 北京: 科学出版社, 2002: 32-66.

Wang Chao, Zhang Hong, and Liu Zhi. Space-borne Synthetic Aperture Radar Interferometry[M]. Beijing: Science Press, 2002: 32-66.

[6] 钟雪莲, 向茂生, 岳焕印, 等. 机载差分干涉SAR的误差分析[J].电子与信息学报, 2010, 32(4): 941-947.

Zhong Xue-lian, Xiang Mao-sheng, Yue Huan-yin,.. Error analysis for airborne differential SAR interferometry[J].&, 2010, 32(4): 941-947.

[7] Macedo K A C de and Scheiber R. Controlled experiment for analysis of airborne D-InSAR feasibility[C]. EUSAR, Ulm, Germany, May 2004.

[8] Macedo K A C de, Andres C, and Scheiber R. On the requirements of SAR processing for airborne differential interferometry[C]. IGARSS, Seoul, Korea, July 2005.

[9] Rosen P A, Hensley S, Joughin I R,.. Synthetic aperture radar interferometry[J]., 2000, 88(3): 333-382.

[10] Fornaro G. Trajectory deviations in airborne SAR: analysis and comparison[J]., 1999, 35(3): 997-1009.

Error Comparison and Analysis of the Two-pass and Three-pass Approaches in Airborne D-InSAR

Li Yan-leiLiang Xing-dongDing Chi-biao

(Institute of Electronics, Chinese Academy of Sciences, Beijing 100190, China)(University of Chinese Academy of Sciences, Beijing 100049, China)

Airborne Differential Synthetic Aperture Radar Interferometry (D-InSAR) is a kind of potential technology to survey the surface deformation. In this paper, the errors of two usually used modes of this technology, namely, two-pass and three-pass approaches, are compared and analyzed. In the analysis, all the errors are decomposed and sorted according to the principle of independence, and the coupling between motion error and other errors is considered. Based on the analysis, analytical expressions are derived for the deformation measurement errors in the two modes. The results demonstrate that when the amplitude of the motion error is small, the three-pass approach can reduce the requirement on the precision of the external topography data, so it distinctly outperforms the two-pass approach; when the amplitude of the motion error is large, high-precision topography data are needed in the three-pass approach, and as a result, its advantage over the two-pass approach is not distinct any more.

Differential interferometry; Airborne Synthetic Aperture Radar (SAR); Error analysis; Two-pass approach; Three-pass approach

TN959.3

A

2095-283X(2013)03-0326-08

10.3724/SP.J.1300.2013.13034

2013-04-01收到，2013-05-09改回；2013-05-20网络优先出版

国家863项目(2013AA122201)和国家973项目(2009CB724003)资助课题

李焱磊 radar_sonar@163.com

李焱磊(1983-)，男，河北定兴人，分别于2007年、2009年获得北京理工大学学士学位和硕士学位，现为中国科学院电子学研究所博士研究生，研究方向为机载差分干涉SAR信号处理。

E-mail: radar_sonar@163.com

梁兴东(1973-)，男，研究员，研究领域包括高分辨率合成孔径雷达系统、干涉合成孔径雷达系统、成像处理及应用和实时数字信号处理。

E-mail: xdliang@mail.ie.ac.cn

丁赤飚(1969-)，男，研究员，研究领域包括信号与信息处理、新体制SAR系统和雷达对抗。

E-mail: cbding@mail.ie.ac.cn