径向基函数神经网络用于毛细管电泳同时检测水中苯二酚、苯酚和对硝基苯酚
2013-07-24孙汉文夏祥华
孙汉文,夏祥华
(河北大学 化学与环境科学学院,河北省分析科学技术重点实验室,河北 保定 071002)
苯酚、苯二酚和硝基苯酚作为重要的化工原料被广泛地用于制造染料、药物、酚醛树脂、胶粘剂等,其属于对环境和人类危害较大的毒性有机物.目前酚类化合物的检测主要有高效液相色谱法[1]、气相色谱法[2]、薄层色谱法[3]、光度法[4]、化学发光法[5-6]、荧光光度法[7].但上述方法存在前处理繁杂、耗时长、成本高,而且因酚类化合物的物理和化学性质的相似性,光谱法也难以实现多组分酚类化合物的同时测定.高效毛细管电泳是近20年迅速发展的一种快速的分离分析技术[8],以其高效、快速,微量操作简单、经济,对样品纯度要求不高及更接近体内的结合行为等优点,被广泛应用于分析测定领域.将毛细管电泳方法用于苯二酚同分异构测定的文献[9-12]已有报道,但就苯二酚、苯酚、对硝基苯酚5组分同时测定的文献未见报道.本文将遗传算法(genetic algorithms,GA)优化输入变量下的径向基函数(radial basis function,RBF)神经网络方法与毛细管电泳方法相结合,用于苯二酚、苯酚、对硝基苯酚5种化合物的同时测定,以“数学分离”替代物理、化学上的分离,实现复杂化学体系的多组分的同时测定,该方法不但准确,快捷,简便,经济,而且不用实现化合物之间的完全分离便可以进行测定.
1 原理与算法
1.1 输入变量优化的实现
遗传算法[13]是一种群体搜索技术,沿多种路线进行平行搜索,为实现群体进化到接近最优解或包含的状态,进行选择、交叉、变异等一系列遗传操作,由当前群体而产生出新一代的群体.一般的GA 由编码机制、控制参数、适应度函数(目标函数)、遗传算子4部分组成.
1)编码的实现:GA 要把问题解编成一个合适的编码.本文采用二进制编码.
2)初始化群体:选择合适的初始群体规模至关重要,规模大小既不易使算法陷入局部最优解,又要使迭代时间不能太长.本文初始种群规模选择20,采用随机取种法产生初始种群的二进制串,每次GA 操作后输入变量优化组合不尽相同[14].因此,本文采用的是平行多次GA 操作,按照输入变量选取概率的大小进行变量优化组合.
3)对象函数:对象函数也称适应度函数,为问题求解品质的测量函数.本文选择通用回归神经网络对每个样本的适应性进行评估.通用回归网络对模型中所包含的非相关性变量较为敏感,且较快的训练速度能够快速完成GA 操作中对大量样本的适应性评估.
4)遗传算法算子的选择、交换、变异:个体的优劣度由算子的选择所决定,算子的选择成为最终为选择它在下一代被复制还是被淘汰的依据.本文选用了轮盘赌选择法.变异和交叉操作的作用主要是防止过早熟,避免收敛过慢.本工作选用单点交叉方式进行父串信息的交换,以便获得质量更优的新解.
本文输入变量选择优化的程序包括2步.
1)对同一输入变量进行平行GA 操作.在GA 操作中,因初始种群产生的随机性和变量之间的偶然相关性,即使对同一数据进行平行遗传操作,输入变量优化组合方式具有相似性,但不完全相同.本文选择平行10次GA 操作进行输入变量优化选取,将变量在所有GA 操作中被选择的概率进行统计,按输入变量被选择概率大小依次增加变量数量.
2)计算不同输入变量模型的预测误差值,预测误差值最小所对应的输入变量组合为输入变量最佳组合.神经网络模型的预测误差均由下式计算.

其中p 代表所有样本的数目;ippred样本p 的预测值;iptrue代表模型样本p 的目标值.
1.2 径向基函数神经网络
径向基函数[14]神经网络是一种单隐层前馈层状型的神经网络,能以任意精度逼近任一连续函数,非常适合于非线性动态系统建模.RBF神经网络模型是基于相关RBF 的线性组合.最常用的RBF 为高斯型函数,其表达式如公式(2)所示.

hj(x;cj;σj)表示隐含层中第j个RBF单元的输出值;║x-cj║表示第j 个网络模型的中心矢量cj和输入变量x 的Euclidean间的距离;σj代表第j 个网络模型的扩展程度.模型的输出公式表示为

其中,ωjk表示输出层单元k 与隐含层单元j 间的连接权重;Yk(x)为输入矢量x 经网络模型计算后的输出层单元k 中的输出值.bk表示输出单元k 的偏置.本文以K-均值算法为RBF模型的中心,且以K-最邻近偏差分配算法进行模型宽度选取.模型的中心和宽度确定之后,将以伪逆训练算法不准进行隐含层单元与输出层单元间的连接权重的调整,并以平方和误差函数监控RBF 网络的训练过程,使最优网络模型的误差函数E最小.E 由公式(4)给出:
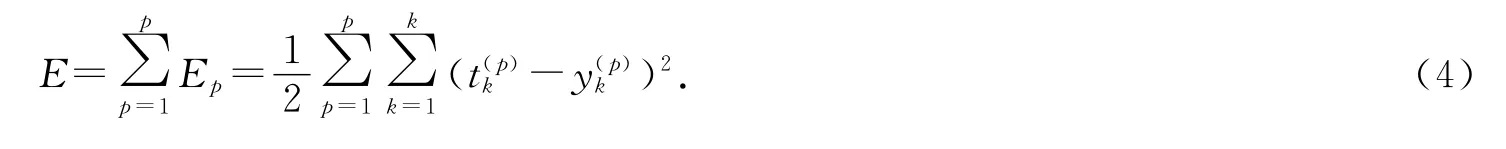
2 实验部分
2.1 试剂和仪器
主要仪器:CL1020型高效毛细管电泳仪(中国北京彩陆科学仪器有限公司);KH-50B型超声波清洗器(昆山禾创超声仪器有限公司);pHS-3C精密pH 计(上海雷磁仪器厂);毛细管为内径100μm 未涂层的熔硅毛细管(河北永年光导纤维厂),总长度为65cm,有效长度57cm.
试剂:邻苯二酚(天津市科密欧化学试剂有限公司);间苯二酚(天津市华东试剂厂);对苯二酚(天津市科密欧化学试剂有限公司);苯酚(天津市科密欧化学试剂开发中心);对硝基苯酚(SCRC国药集团化学试剂有限公司);磷酸二氢钾(KH2PO4);磷酸氢二钠.所用试剂均为分析纯,水为二次重蒸水,所有上机溶液均需经0.45μm滤膜处理.
2.2 样品的制备
分别准确称量0.025g邻苯二酚、间苯二酚、对苯二酚、苯酚和对硝基苯酚分别于100mL容量瓶中,加水稀释、定容,作为储备液放置于冰箱内,用时逐级稀释.在5.4~230.0μg/mL内,配置邻、间、对苯二酚、苯酚和硝基苯酚5组的混合溶液实验样本30个.
2.3 实验方法
用稀盐酸调节磷酸盐缓冲体系的酸度pH 8.17;实验前依次用NaOH 溶液(0.1mol/L)、H2O、缓冲溶液冲洗毛细管各10min,高效毛细管电泳仪的检测波长为200nm,分离操作电压为10kV,重力进样高度15cm,时间为10s;每2个样品分析后冲洗3min.在本文优化条件下,采集30个样品的毛细管电泳谱图.
本实验所需程序均由MATALAB编写和运行.数据采集和处理由ACS-2000工作站进行分析和评估.以ASCⅡ码文件格式表述光谱图数据.所用计算程序在PC计算机上运行.
3 结果与讨论
3.1 缓冲溶液的影响
缓冲溶液的pH 直接影响着电渗流的大小进而影响分离的效果.由于苯二酚、苯酚和对硝基苯酚结构相近、化学及物理性质相似,邻苯二酚、间苯二酚、对苯二酚、苯酚和对硝基苯的pKa值分别为9.4,9.4,10.3,10.0和7.09,在磷酸二氢钾和磷酸氢二钠的缓冲体系下,本文考察了溶液pH 在5.80~9.00内对样品测定的影响.综合考虑选择缓冲体系pH 为8.17进行分离.图1为在本实验优化条件下邻苯二酚、间苯二酚、对苯二酚、苯酚和对硝基苯酚5组分混合溶液的毛细管电泳谱图.
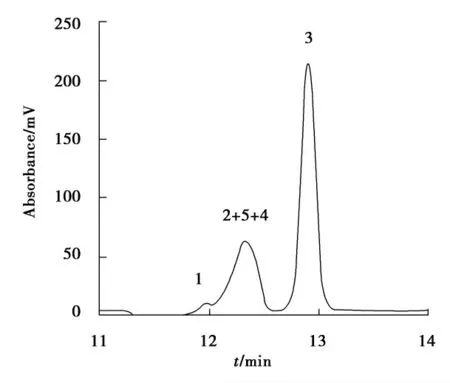
图1 检测波长200nm 5组分的毛细管电泳Fig.1 Electrophoretogram of the five compounds at 200nm
3.2 运行电压的影响
在磷酸盐缓冲体系下pH 为8.17,温度20 ℃,在5~20kV 电压下对5种物质进行分离.研究发现电压对分离影响较小,但是随电压和温度升高,迁移时间缩短.综合考虑分离效果和分析速度,选择电压为10kV,温度为20 ℃,在15min内可完成5种物质的分离.
3.3 毛细管电泳图的解析
将优化条件下采集的30个5组分混合样品的毛细管电泳图的数据点作为神经网络的训练样本,从训练集中均匀选取7个样本作为神经网络模型训练的校正集,用于监控神经网络的训练过程,避免“过训练”的发生,且使神经网络模型平行运行10次,以检验神经网络运行的稳定性.如果从毛细管电泳谱图上均匀选取81个数据点都作为神经网络模型的输入变量,输入变量显然过多,不相关的、冗余的以及含有噪声的变量可能也被包含在输入数据集中,有意义的变量可能被隐藏[16],这就使得过大数量的输入变量间偶然相关的概率大大增加[17],且大数量的输入变量也使得相关神经网络模型难以进行优化[18].因此,有必要进行模型输入变量的优化.选择GA 对初次选取的变量进行优化操作,即使有校正程序存在的情况下,GA 的每次平行操作往往输入变量具有相似性但不完全相同,因此,本文作者采用平行运行10次GA 操作(遗传代数为100代,种群规模为20,变异率为1,交叉率为0.3,惩罚因子为0.1).在单次的GA 操作中,最后一代群体中的变量被记录下来,对这些变量在所有GA 操作中出现的概率进行统计,概率大小依次排列,逐一增加输入变量,最终将所有变量均加入变量集,根据预测误差大小,选出合适的输入变量.预测误差最小所对应的变量为最佳输入变量,本文将“去-交叉校验法”用于检验网络模型的预测能力.“去-交叉校验法”是将数据集中的任意1个样本剔除,剔除的样本作为未知样本对训练好的模型进行测试,最后使得每一个样本均作为一次未知样本对训练好的模型进行测试,根据预测结果对模型进行评估,将采集的30个5组分样本的谱图数据(81个)平行进行10次GA 操作后,变量选取概率如图2所示.不同输入变量所对应的预测误差如图3所示,选取41个输入变量时RBF神经网络模型的预测误差最小,即选取概率从50%~100%的所有变量最合适.对样品分析的预测误差和标准偏差在表1中均被列出.
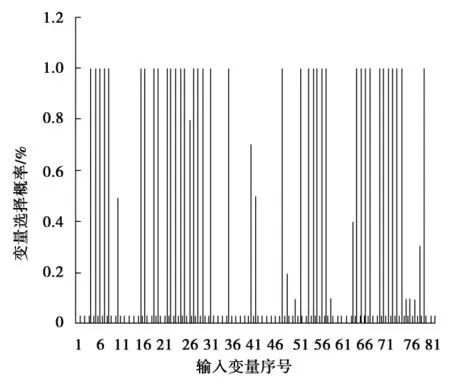
图2 5组分数据点被遗传算法选择的概率Fig.2 Frequency of the data points of five component being selected by genetic input selection

图3 优化选取输入变量对应的预测误差Fig.3 Optimization of the input variable corresponding to the prediction errow
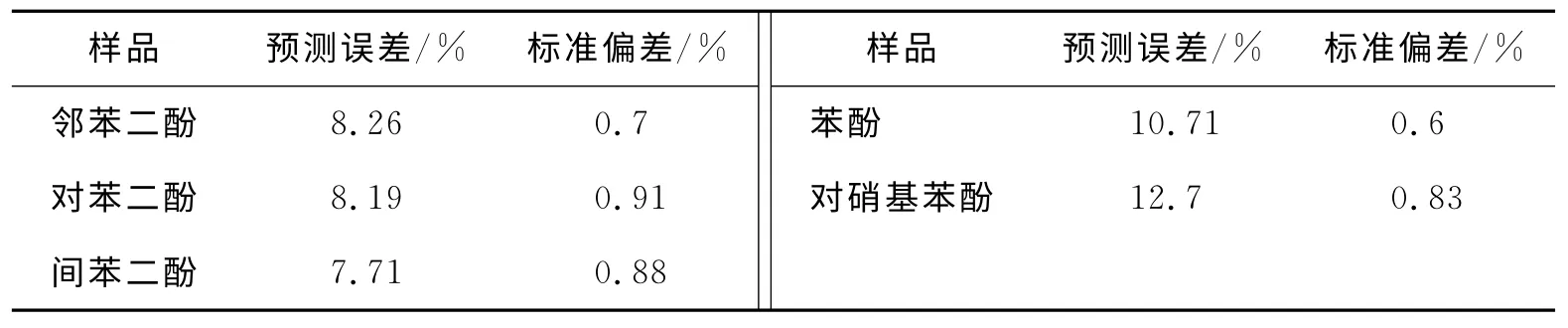
表1 径向基函数的预测误差和标准偏差Tab.1 Result of prediction errors and standard deviation of RBF NN
将毛细管电泳-遗传算法优化输入变量下的径向基函数神经网络方法用于同时检测水中5组分邻、间、对苯二酚、苯酚和对硝基苯酚,可有效解决由毛细管电泳对苯二酚、苯酚和对硝基苯酚5组分的分离不理想,给定量检测带来的困难.本文建立了水样中苯二酚、苯酚、对硝基苯酚5组分的同时测定的新方法,具有较高的检测灵敏度和精密度,可有效地同时检测水样中多种苯的衍生物.
[1] CUI Hua,HE Caixia,ZHAO Guiwen.Determination of polyphe-nols by high-performance liquid chromatography with inhibited chemiluminescence detection[J].Chromatogr A,1999,855:171-179.
[2] MOLDOVEANU S C,KISER M.Gas chromatography/mass spectrometry versus liquid chromatography/fluorescence detection in the analysis of phenols in mainstream cigarette smoke[J].Journal of Chromatography A,1141:90-97.
[3] 黄少鹏,徐金瑞,王琼.薄层色谱法同时测定邻苯二酚、间苯二酚和对苯二酚异构体[J].分析化学,1999,27(3):331-333.HUANG Shaopeng,XU Jinrui,WANG Qiong.Simultaneous determination of o-,m- ,p-dihydroxybenzene isomer by thin-layer chromatography[J].Chinese Journal of Analytical Chemistry,1999,27(3):331-333.
[4] 耿玉珍,刘葵,刘连伟.吸光度比值导数法同时测定苯酚、邻苯二酚和对苯二酚[J].分析化学,1997,25(9):1024-1210.GENG Yuzhen,LIU Kui,LIU Lianwei.Simultaneous determination of phenol,catechol and hydroquinone by absorbance ratio derivative method[J].Chinese Journal of Analytical,1997,25(9):1024-1210.
[5] LI Shifeng,LI Xiangzhi,XU Jing,et al.Flow-injection chemiluminescence determination of polyphenols using luminol-NaIO4-gold nanoparticles system[J].Talanta,2008,75:32-37.
[6] SUN Yugang,CUI Hua,LI Yinghui,et al.Determination of some catechol derivatives by a flow injection electrochemiluminescent inhibition method[J].Talanta,2000,53:661-666.
[7] PISTONESI M F,DINEZIO M S,CENTURION M E,et al.Determination of phenol,resorcinol and hydroquinone in air samples by synchronous fluorescence using partial least-squares(PLS)[J].Talanta,2006,69(5):1265-1268.
[8] 陈义.毛细管电泳技术及应用[M].北京:化学工业出版社,2000.
[9] ZHANG Yaxiong,LI Hua,HOU Aixia,et al.Artificial neural networks based on genetic input selection for quantification in overlapped capillary electrophoresis peaks[J].Talanta,2005,65:118-128.
[10] 张裕平,熊辉,袁倬斌.硝基苯类化合物的高效毛细管电泳的分离测定[J].分析化学,2001,29(12):1481.ZHANG Yuping,XIONG Hui,YUAN Yibin.Determination of nitrobenzene compounds by high performance capillary electrophoresis[J].Chinese Journal of Analytical,2001,29(12):1481.
[11] 刘学良,王进防,王俊德,等.毛细管区带电泳法快速分离硝基酚和除草剂[J],色谱,2001,19(2):173-175.LIU Xueliang,WANG Jinfang,WANG Junde,et al.Sensitive and rapid analysis of nitrophenols and herbicides by capillary zone electrophoresis(CZE)[J].Chinese Journal of Chromatography,2001,19(2):173-175.
[12] 刘学良,王进防,王俊德,等.毛细管电泳中获得稳定电渗流的毛细管预处理方法[J].分析化学,2000,28(9):1110-1113.LIU Xueliang,WANG Jinfang,WANG Junde,et al.A Procedure for obtaining reproducible results in capillary electrophoresis[J].Chinese Journal of Analytical,2000,28(9):1110-1113.
[13] SHAO Xueguang,CHEN Zonghai,LIN Xiangqin.Resolution of multicomponent overlapping chromatogram using an immune algorithm and genetic algorithm[J].Chemometricsand Intelligent Laboratory Systems,2000,50:91-99.
[14] ARCOS M J,ORTIZ M C,VILLAHOZ B A,et al.Genetic-algorithm-based wavelength selection in multicomponent spectrometric determinations by PLS:application on indomethacin and acemethacin mixture[J].Anal Chim Acta,1997,339:63-77.
[15] DAVID V,SANCHEZ A.Searching for a solution to the automatic RBF network design problem[J].Neurocomputing,2002,421(4):147-170.
[16] SEASHOLTZ M B,KOWALSKI B R.The parsimony principle applied to multivariate calibration[J].Anal Chim,Acta,1993,277:165-177.
[17] LIVINGSTONE D J,MANALLACK D T.Statistics using neural networks:chance effects[J].Med Chem,1993,36:1295-1297.
[18] BROADHURST D,ROWLAND J J,KELL D B.Genetic algorithms as a method for variable selection in multiple linear regression and partial least squares regression,with applications to pyrolysis mass spectrometry[J].Anal Chim Acta,1997,348:71-86.
