例谈微分方程在实际问题中的简单应用
2013-07-24辛春元
辛春元
(辽宁对外经贸学院,辽宁大连116052)
例谈微分方程在实际问题中的简单应用
辛春元
(辽宁对外经贸学院,辽宁大连116052)
微分方程在物理学、力学、经济学和管理科学等实际问题中具有广泛的应用,本文主要例谈微分方程在实际问题中的简单应用.
微分方程;实际问题;应用
微积分研究的对象是函数关系,但在实际问题中,往往很难直接得到所研究的变量之间的函数关系,却比较容易建立起这些变量与它们的导数或微分之间的联系,从而得到一个关于未知函数的导数或微分的方程,即微分方程.通过求解这种方程,同样可以找到指定未知量之间的函数关系.因此,微分方程是数学联系实际,并应用于实际的重要途径和桥梁,是各个学科进行科学研究的强有力的.下面举几个实际例子.
1 追迹问题
例1设开始时甲、乙水平距离为1单位,从A点沿垂直于OA的直线以等速v0向正北行走;甲从乙的左侧O点出发,始终对准乙以mv0(n>1)的速度追赶.求追迹曲线方程,并问乙行多远时,被甲追到.
解设所求追迹曲线方程为y=y(x)经过时刻t,甲在追迹曲线上的点为P(x,y)乙在点B(1,v0t).于是有

由题设,曲线的弧长OP为
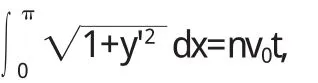
解出v0t代入(1),得
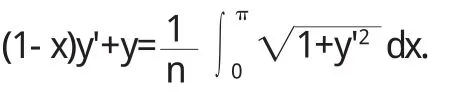
两边对x求导,整理得
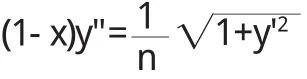
这就是追迹问题的数学模型.
这是一个不显含y的可降阶的方程,设y'=p(x),y"=p",代入方程得

两边积分,得
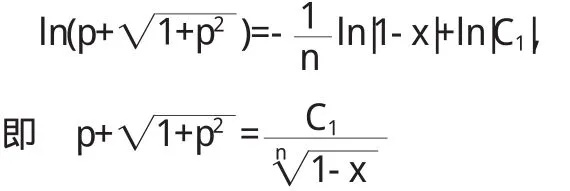


(2)与(3)式相加,得
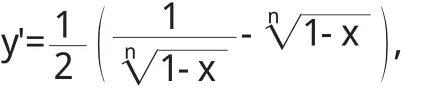
两边积分,得


2 新产品推广模型
例2设有某种新产品要推向市场,t时刻的销量为x(t),由于产品性能良好,每个产品都是一个宣传品,因此,t时刻产品销售的增长率与x(t)成正比,同时,考虑到产品销售存在一定的市场容量N,统计表明与尚未购买该产品的潜在顾客的数量N-x(t)也成正比,于是有

其中k为比例系数.分离变量积分,可以解得

当x(t*) 国内外许多经济学家调查表明,许多产品的销售曲线与公式(5)的曲线(逻辑斯谛曲线)十分接近.根据对曲线性状的分析,许多分析家认为,在新产品推出的初期,应采用小批量生产并加强广告宣传,而在产品用户达到20%到80%期间,产品应大批量生产;在产品用户超过80%时,应适时转产,可以达到最大的经济效益. 例3某种商品的价格变化主要服从市场供求关系.一般情况下,商品供给量S是价格P的单调递增函数,商品需求量Q是价格P的单调递减函数,为简单起见,分别设该商品的供给函数与需求函数分别为 其中a,b,α,β均为常数,且b>0,β>0. 当供给量与需求量相等时,由(7)可得供求平衡时的价格 并称Pe为均衡价格. 一般地说,当某种商品供不应求,即S 其中k>0,用来反映价格的调整速度. 将(6)代入方程,可得 其中常数λ=(b+β)k>0,方程(7)的通解为 假设初始价格P(0)=P0代入上式,得C=P0-Pe,于是上述价格调整模型的解为 由于λ>0知,t→+∞时,P(t)→Pe,说明随着时间不断推延,实际价格P(t)将逐渐趋近均衡价格Pe. 例4每年大学毕业生中都要有一定比例的人员留在学校充实教师队伍,其余人员将分配到国民经济其他部门从事经济和管理工作.设t年教师人数为x1(t)科学技术和管理人员数目为x2(t),又设1外教员每年平均培养α个毕业生,每年人教育、科技和经济管理岗位退休、死亡或调出人员的比率为δ(0<δ<1),β表示每年大学生毕业生中从事教师职业所占比率(0<δ<1),于是有方程 方程(8)有通解 将(11)代入(9)方程变为 求解方程(12)得通解 (11)式和(14)式分别表示在初始人数分别为x1(0),x2(0)情况,对应于β的取值,在t年教师队伍的人数和科技经济管理人员人数.从结果看出,如果取β=1,即毕业生全部留在教育界,则当t→∞时,由于α>δ必有x1(t)→+∞而x2(t)→0,说明教师队伍将迅速增加.而科技和经济管理队伍不断萎缩,势必要影响经济发展,反过来也会影响教育的发展.如果将β接近于零.则x1(t)→0,同时也导致x2(t)→0,说明如果不保证适当比例的毕业生充实教师选择好比率β,将关系到两支队伍的建设,以及整个国民经济建设的大局. 例5在上平面求一条上凹的曲线,其上任意一点p(x, y)处的曲率等于此曲线在该点的法线段PQ长度的倒数(Q是法线与x轴的交点),且曲线在点(1,1)处的切线与x轴平行. 解设所求曲线的方程为y=y(x)(y>0),其在任意一点p (x,y)处的法线方程为,它与x轴的交点是Q (x+yy',0),从而线段PQ长度为 由于y">0,得方程yy"=1+y'2,且满足初始条件:y(1)=1,y' (1)=0.这是不显含x的可降阶方程,令p=y',有y",代入方程得,分离变量得,两边积分的,即,代入初始条件y(1)=1,y'(1)=0,得C1=1,因此有,即,两边积分得)=±x+C,代入y(1)=1得C=μ1,所求曲线方程为 总之,微分方程是与微积分一同发展起来的重要的数学分支,它为解决实际问题提供了一种既实用又很重要的方法,同时推动了其他学科的发展. 〔1〕吴赣昌.微积分[M].北京:中国人民大学出版社,2006. 〔2〕曹显兵,刘喜波.高等数学(微积分)辅导讲义[M].北京:海豚出版社,2012. O175 A 1673-260X(2013)11-0001-023 价格调整模型


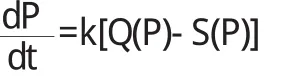

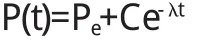

4 人才分配模型
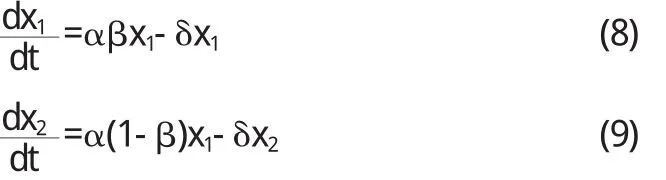


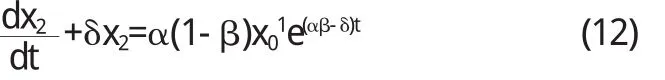


5 几何问题模型