基于GARCH模型的我国股市风险分析
2013-07-22张亮旭卓荣康
张亮旭,卓荣康
(兰州商学院金融学院,甘肃兰州730020)
基于GARCH模型的我国股市风险分析
张亮旭,卓荣康
(兰州商学院金融学院,甘肃兰州730020)
通过对上证指数收盘指数进行实证分析,采用正态分布、t分布和GED分布分别刻画收益率序列特征,运用GARCH模型对收盘指数序列进行波动性建模.根据GARCH模型的估计结果计算出VaR和CVaR值.由结果可知,通过计算GED分布下的GARCH(1,1)模型的CVaR值是衡量股市风险的最佳模型.
上证指数;GARCH模型;VaR方法;CVaR方法
1 引言
1.1 背景
我国股票市场处于发展初期,起步于计划经济向市场经济转型的环境中,存在种种缺陷,具有与发达成熟市场不同的特点.而且,随着美国次贷危机的爆发对全世界金融领域的冲击,更加加剧了中国股市的剧烈波动和风险系数.所以,如何用更加谨慎科学的方法对其风险进行正确的度量、分析和管理,对于金融机构加强风险管理和国家制定监管制度具有重大意义.
本文选取VaR和CVaR两种市场风险测度方法.波动率的计算通过GARCH模型族计算而得,且根据金融资产收益序列的尖峰、厚尾现象假设收益率服从正态分布、t布和GED分布(广义误差分布)三种情况,通过通过比较真实值,得出最佳的估计模型.
1.2 文献综述
目前金融市场风险测量的主流方法是VaR(Value-at-Risk)方法.VaR是一定的置信水平下,资产或资产组合在未来特定一段时间内的最大可能损失.根据Jorion(1996)[1]VaR可定义为
VaR=E(w)-w*E(w)为资产的预期价值,w为资产的期末价值,w*为置信水平下资产的最低期末价值.若设w0为持有期初资产价值,R为回报收益率,持有年限为Δt,R*为资产在置信水平下的最低收益率,zα为在一定分布下置信水平为α的函数返回值,σt为收益率的方差,则
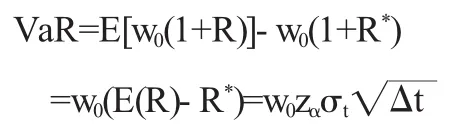
条件风险值(conditional value at risk,CvaR)是继VaR之后产生的又一种风险度量方法.根据Uryasev[2]与Rockafellar[3]的定义,CVaR是超过VaR的损失的期望值.更为确切的是指在一定的置信水平下,某一资产或资产组合的损失超过VaR的尾部事件的期望值.用公式表示为
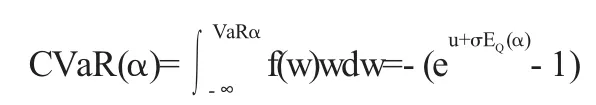
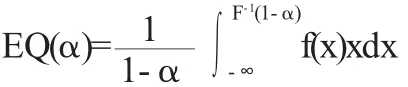
式中:α为置信水平,w为资产的价值,f(w)为概率密度函数,VaRα为置信水平α下的风险值,F-1是逆累积分布函数,f(x)为密度分布函数,u和α为收益序列的特征参数.
对VaR和CVaR的计算和预测其实质是对波动率的计算和预测.1952年,Markowitz提出均值-方差模型来描述资产或资产组合收益率的波动性,开创了金融市场风险测度的定量的方法,标志着现代组合投资理论的开端.Engle(1982)[4]提出自回归条件异方差(ARCH)模型,将条件方差作为过去误差的函数而变化,解决了异方差问题,提高了模型的准确度.在此基础上Bollerslev(1986)[5]提出了广义自回归条件异方差(GARCH)模型.GARCH模型比ARCH模型滞包含的滞后结构要更加宽泛准确.GARCH(1,1)模型可以表示为:
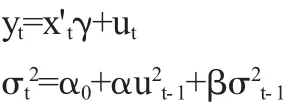
第一个方程为条件均值方程,Xt是解释变量向量,γ是系数向量.第二个方程为条件方差方程,其中,第一项为常数项α0,第二项用均值方程的扰动项的平方的滞后来度量从前期等到的波动性信息u2t-1,第三项上一期的预测方差σ2t-1.
为了描述时间序列受自身方差影响,Engle,Lilien和Robins(1987)[6]提出了GARCH-M模型.为了描述证券市场中的非对称效应,Zakoian(1990)[7]最早提出的TARCH模型,Nelson(1991)[8]提出的EGARCH(指数GARCH)模型既能描述条件异方差性,又能反映杠杆效应.优点是用成指数形式表示条件异方差,对参数没有任何约束.Taylor(1986)和Schwert(1989)介绍了标准差的GARCH模型,这个模型模拟的不是方差而是标准差.这样大幅冲击对条件方差的影响比在标准的GARCH模型中要小.Ding et al.(1993)[9]对该模型进一步拓展提出PARCH(Power ARCH)模型.
由于受到市场发展水平、参与者理性程度及其对利好和利空信息的反应不同等众多因素的影响,股票收益率序列往往不是正态分布,然而一般的研究却没有充分考虑收益率的分布特征,因此本文假设收益率符合三种分布:正态分布、学生t分布、GED分布,并分别计算VaR和CVaR值,已达到更好解释收益序列的尖峰厚尾和波动率聚类现象.
2 实证研究
2.1 数据选取
本文选取上证指数在1000个交易日的收盘指数作为样本数据,区间为2009年1月21日~2013年3月6日.本文数据来源于钱龙证券投资分析系统.本文采用Eviews6.0和Mathematica8.0软件对数据进行处理及分析.
2.2 统计性描述
本文采用对数收益率对上证指数进行研究,表达式如下:
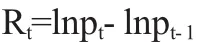
其中:pt表示第t个交易日的收盘指数,Rt为日对数收益率.
从图1可以看出,上证指数收益率有着明显的波动聚集性,即有相似特征的波动成群出现,高收益率与高收益率聚集,低收益率与低收益率聚集.而且,收益率在相对集中的区域有着较大的波动,有着明显的异方差性.从图2可以看出,上证指数收益率均值为0.000168,标准差为0.014252,都不是很大,但是偏度为-0.401837,峰度为5.102900,比较正态分布可以得出,序列是左偏且有“尖峰厚尾”特征.J-B为210.9588,其P值为0,更进一步说明上证指数收益率序列不服从正态分布,故应采用其学生t分布或GED分布进行回归分析.
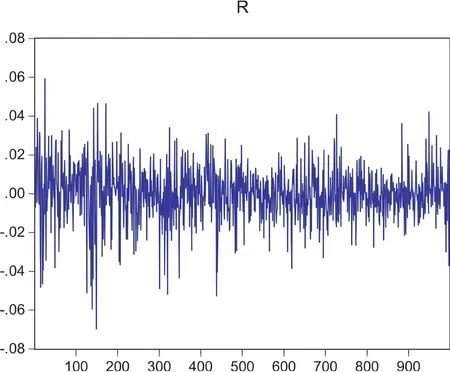
图1 上证指数日收益率序列图
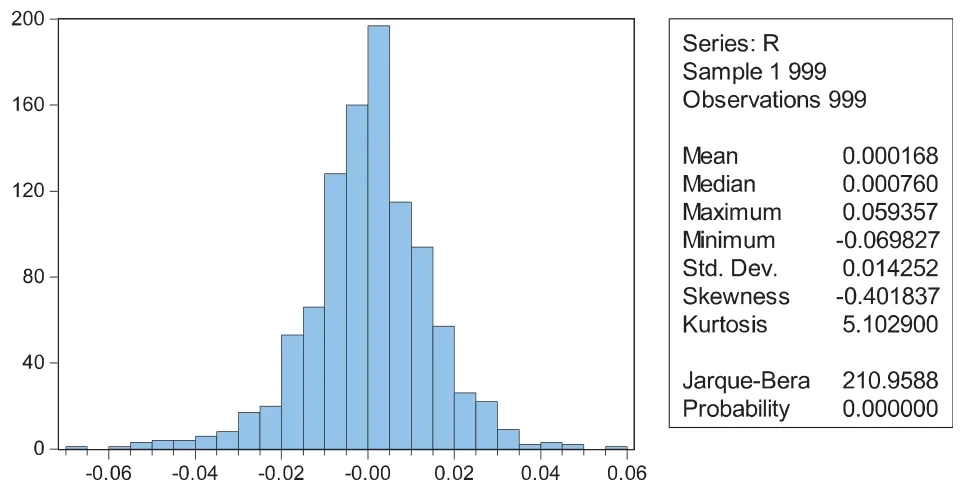
图2 上证指数日收益率序列描述性统计
2.3 平稳性检验

表1 上证指数日收益率序列单位根检验
为了防止伪回归的出现,我们对收益率序列进行ADF单位根检验,以保证序列是平稳的,结果如表1所示.
由表1可看出,ADF-t统计量的绝对值远大于1%、5%、10%水平下的绝对值,且ADF-t统计量P值为0,则拒绝原假设,说明不存在单位根,序列是平稳序列.
2.4 自相关和偏自相关检验
根据序列的自相关和偏相关系数及Q统计量,可以确定自回归项的阶数,以便建立均值方程.我们对收益率序列进行滞后12阶的自相关与偏自相关检验,由图3可以看出,自相关与偏自相关系数均落入两倍的估计标准差内且自相关与偏自相关系数接近于零,而且Q统计量对应的p值都大于0.05,即收益率序列不存在明显的相关关系,因此,均值方程中不引入自相关描述部分.
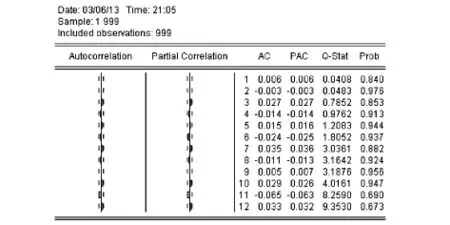
图3 上证指数日收益率序列自相关和偏自相关检验
2.5 建立GARCH模型族
2.5.1 均值方程的建立
有上述分析可知,上证指数日收益率序列具有尖峰、后尾的特征,其波动波动聚集性等特征,如果在正态分布下估计Var和CVaR值容易高估风险,因此我们选用t分布和GED分布对Var和CVaR值进行估计;且收益率序列不存在明显的相关关系,因此我们以收盘指数为对象建立以下模型:
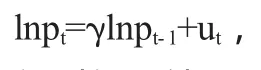
回归得到如下结果:
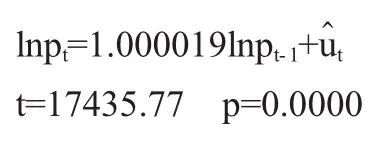

表2 均值方程3阶ARCH-LM检验
R2=0.989214,AIC=-5.662787,SC=-5.657875
图4 均值方程残差平方相关图
从结果看,方程有较好的拟合效果,为了检验是否存在ARCH效应,我们对残差进行了ARCH-LM检验,发现存在着3阶的ARCH效应,并从残差平方相关图可以得到证实.考虑到存在高阶的ARCH效应,应建立GARCH模型.经过反复实验,用GARCH(1,1)模型取得较好的效果.
2.5.2 GARCH(1,1)模型的建立
条件均值方程为lnpt=lnpt-1+ut,
条件方方差方程为σt2=α0+αu2t-1+βσ2t-1
从模型的估计结果来看,三种分布下γ,α,β的估计值在1%的水平下均显著,方程的拟合度提高,AIC和SC值有所下降,α0,α,β非负且三者之和小于1,满足约束条件,说明GARCH(1,1)模型能较好的模拟收益率波动情况.而且对残差进行GARCH-LM检验及从残差平方相关图可以明显看出,模型已不存在ARCH效应.
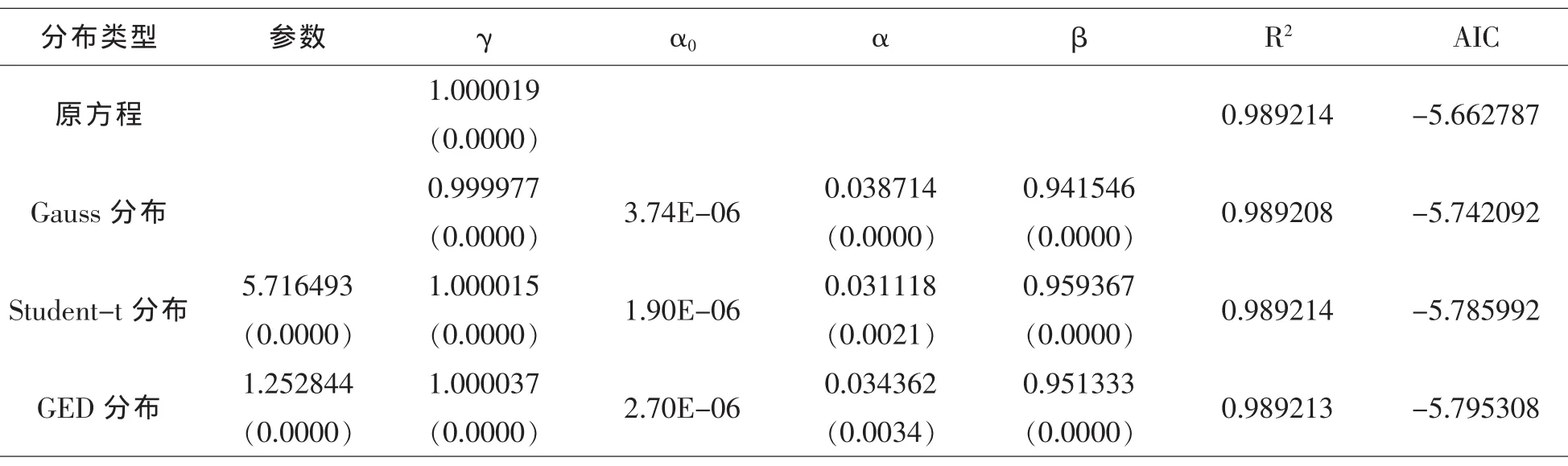
表3 三种分布下GARCH(1,1)模型的估计结果及和原方程的对比

表4 GARCH(1,1)-gauss模型的1阶ARCH-LM检验
2.5.3 EGARCH(1,1)模型建立
条件均值方程为lnpt=γlnpt-1+ut,条件方差方程为
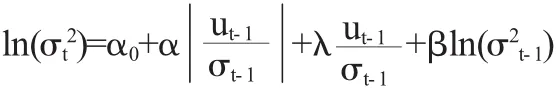
当ut-1≥0时,α+λ倍冲击;当ut-1<0时,λ-α倍冲击.
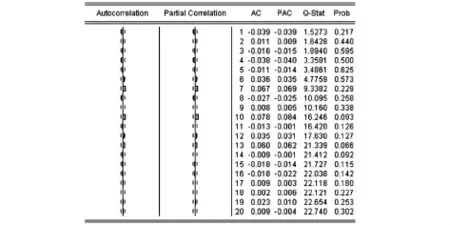
图5 GARCH(1,1)-gauss模型的残差平方相关图
从表5的结果来看,参数λ不显著,拟合度有所降低,但AIC值有所降低.但GARCH-LM检验及从残差平方相关图可以看出,此模型也同样不存在ARCH效应.
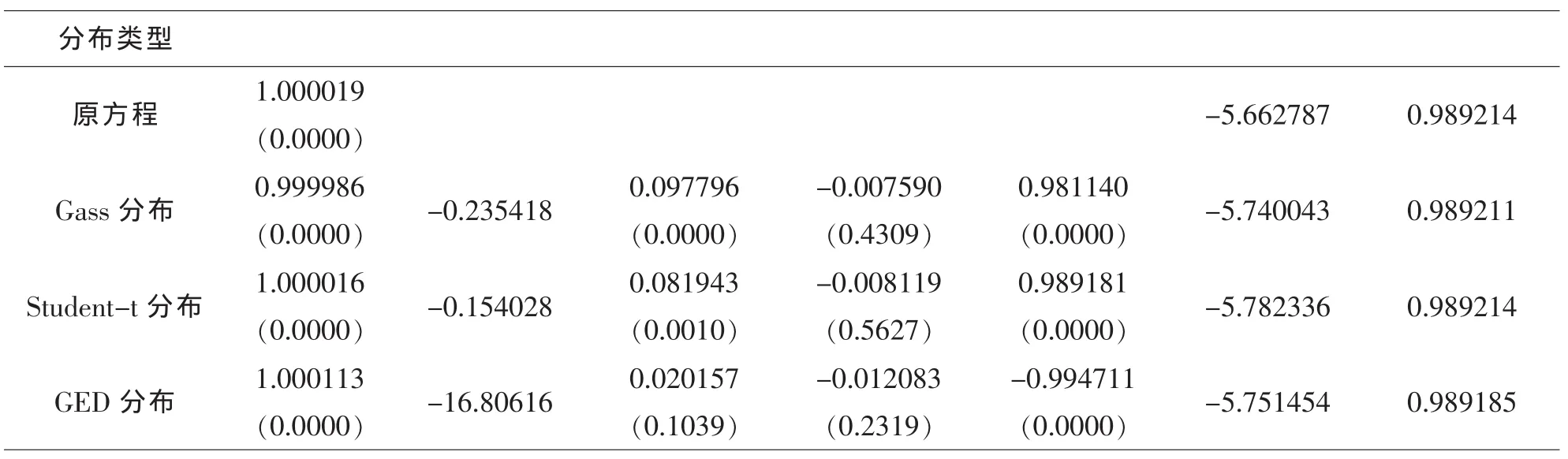
表5 三种分布下EGARCH(1,1)模型的估计结果
2.5.4 GARCH(1,1)模型和EGARCH(1,1)模型估计结果分析
从表3和表5可以看出,GARCH(1,1)模型和EGARCH(1,1)模型中参数的估计值都小于或接近零,说明我国股票的平均收益率水平为负,投资风险较大.参数都大于零说明了价格的波动聚集性特征,即过去价格的波动对市场未来的波动有着正向但减弱的影响,大幅度波动后面一般紧随着更大幅度的波动,小幅度波动后面一般紧随着跟小幅度的波动,但是这种影响慢慢减弱,说明我国股市参与者投机性较强,羊群效应明显.参数β明显大于α,这意昧着意外信息对未来价格的波动产生相对较小的影响,说明我国国股票市场不易受到意外信息影响,主要受上期波动的影响.由于模型中α+β的值均非常接近于1,说明我国股票市场的波动具有持续性,当前的信息对预测未来的价格波动即条件方差很重要.
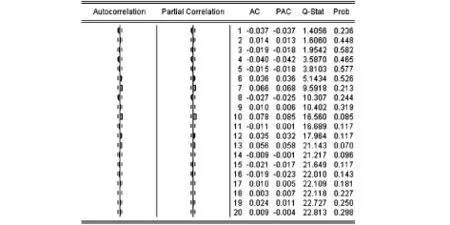
图6 EGARCH(1,1)-gauss模型的残差平方相关图

表6 EGARCH(1,1)-gauss模型的1阶ARCH-LM检验
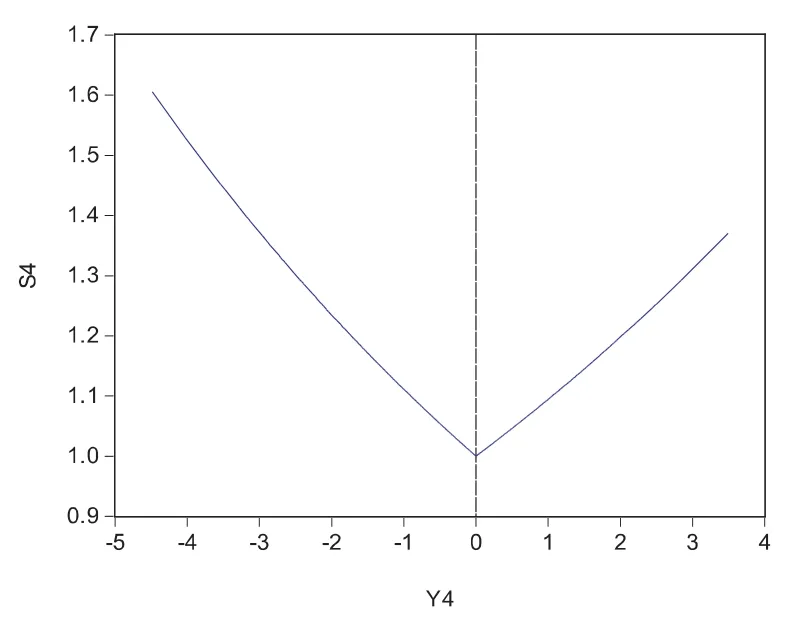
图7 Gauss分布下ut/σt冲击对波动率σt2的影响曲线
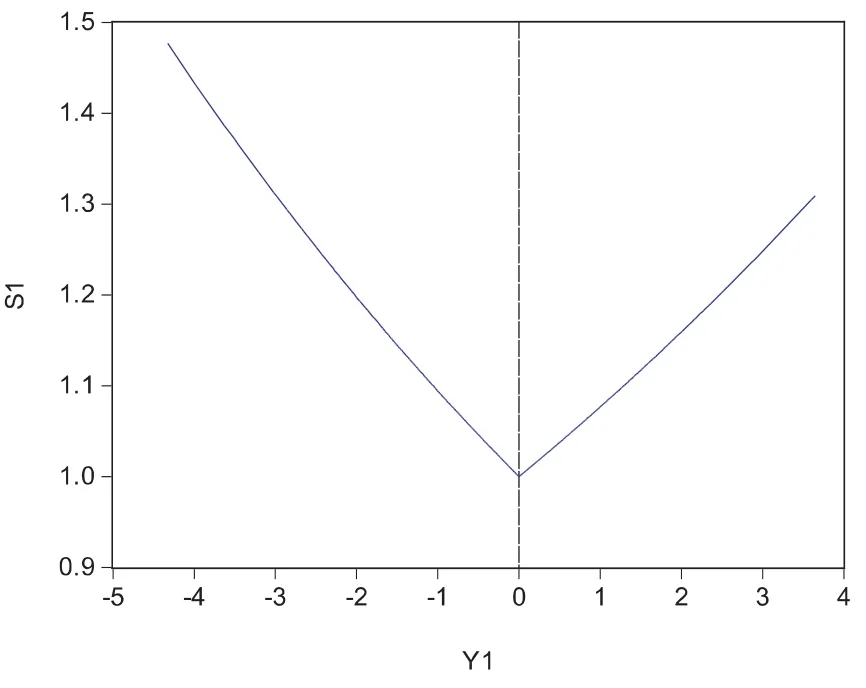
图8 Student-t分布下冲击ut/σt对波动率σt2的影响曲线
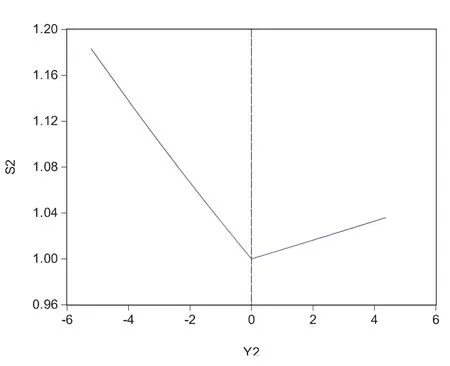
图9 GED分布下冲击ut/σt对波动率σt2的影响曲线
参数λ小于零表示利空消息对股票价格波动的影响大于利好消息的影响.从三种分布的ut/σt冲击对波动率σt2的影响曲线图,我们可以得到,在gauss分布下,当ut-1≥0时,0.090206倍冲击;当ut-1<0时,-0.105386倍冲击.同理,在Student-t分布下,当ut-1≥0时,0.073824倍冲击;当ut-1<0时,-0.090062倍冲击;在GED分布下,当ut-1≥0时,0.008074倍冲击;当ut-1<0时,-0.03224倍冲击.这跟我们现实相符,利空消息对股价的的影响往往利好的消息影响大.在利好的消息下,gauss分布下波动率σt2的影响最大,曲线右侧较陡;在利空的消息下,gauss分布下波动率σt2的影响最大,曲线左侧较陡.而且可以看出,GED分布的非对称性最大.
2.6 VAR及CVAR计算
由于EGARCH(1,1)模型中参数λ不显著,所以我们选择GARCH(1,1)模型计算出条件标准差的估计值,代入公式求VaR值和CVaR值,并采用失败检验法检验.
从表6的计结果来看,在95%的置信水平下GARCH(1,1)-gauss模型中,股票持有者每天面临的最大损失不超过118.9671,平均损失不超过59.93239.在GARCH(1,1)-t下风险均值最大,标准差也最大,说明t分布计算的VaR值和CVaR值波动最大,VaR值和CVaR值是最分散的.在GARCH(1,1)-gauss下VaR均值最小,标准差也最小,而在GARCH(1,1)-GED下CVaR均值最小,标准差也最小,说明VaR值在GARCH(1,1)-gauss下波动最小,CVaR值在GARCH(1,1)-GED下波动最小.
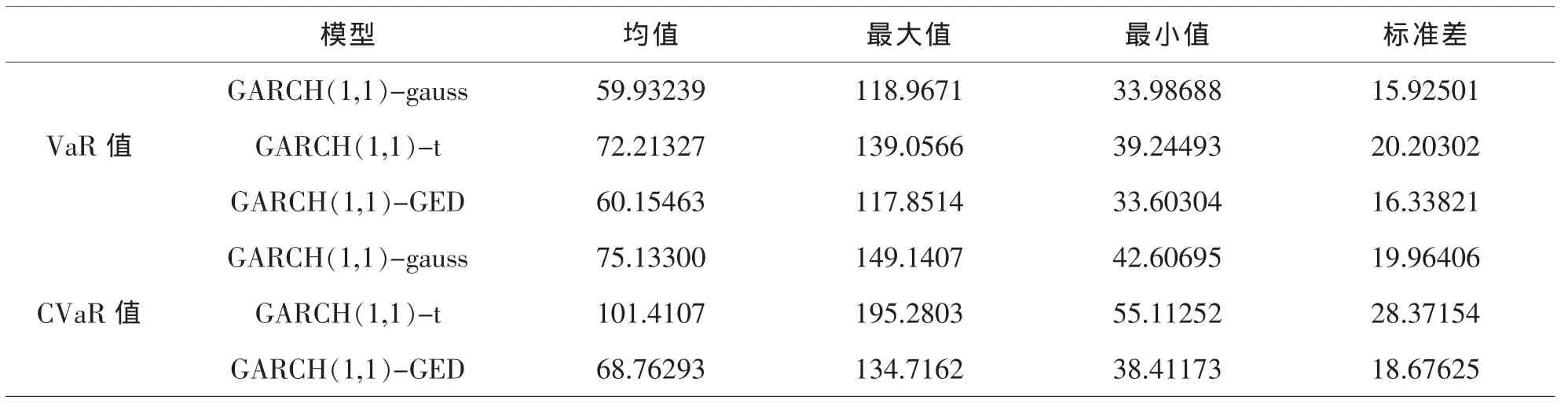
表6 GARCH(1,1)模型的VAR及CVAR值序列的统计量
从表7的结果可以看出,失败率在95%置信水平下都位于4%附近,CVaR值比VaR值的实际失败率较小,说明CVaR较VaR高估风险,是一种更保守的计算.从GARCH(1,1)模型和EGARCH(1,1)模型估计结果来看,沪市股票的均衡收益率水平为负,市场的风险较大且有较大集群特征和投机性,因此应选择较保守的投资策略,用CVaR值衡量股市风险更为合理.使用Kupiec[10]的似然比率检验方法进行模型的有效性检验,发现LR统计量在95%置信水平下的临界值为3.841,只有GARCH(1,1)-GED下的VaR和CvaR通过了检验.此外,CVaR值在GARCH(1,1)-GED下波动最小,因此我们选择GARCH(1,1)-GED模型更为合理.
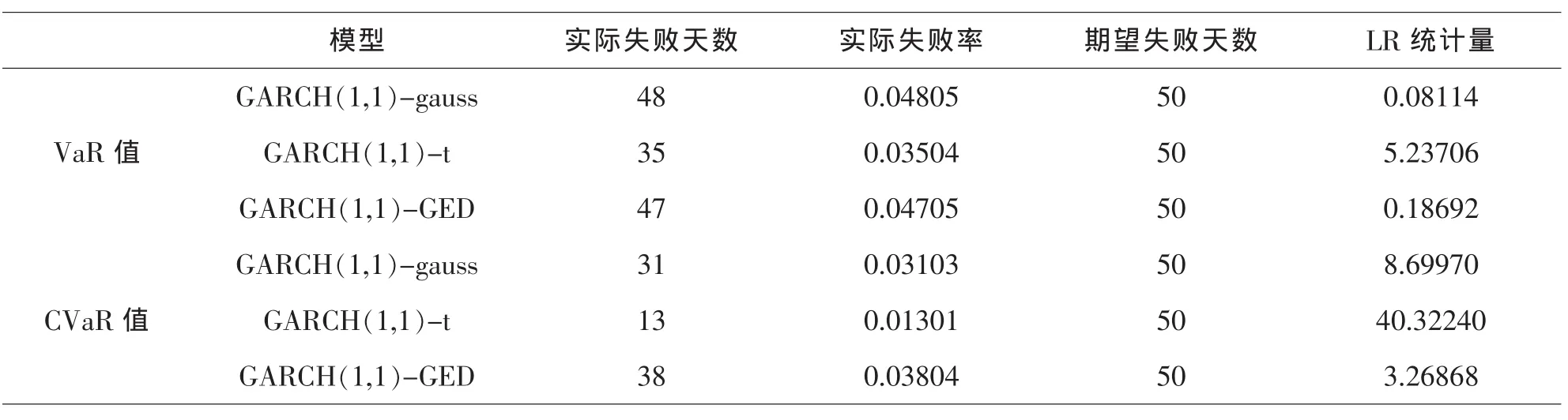
表7 GARCH(1,1)模型的VAR及CVAR值的实际失败率
3 结论
本文对上证指数的收盘指数序列进行了GARCH模型和EGARCH模型的波动性建模,以GARCH模型为基础计算得到不同分布假设下的VaR和CVaR估计值,以EGARCH模型为基础研究其不对称性,并得到以下结论:
3.1 上证指数日收益率序列具有尖峰、厚尾和波动聚集性等特征,如果按通常的正态分布假设估计VaR值和CVaR值容易高估风险,因此应选用t分布或GED分布假设更合理;且收益率序列不存在明显的相关关系,不能用ARCH模型建立起均值方程,因此我们以收盘指数建模型,取得较好的拟合效果.
3.2 分别建立在三种分布下的GARCH(1,1)模型和EGARCH(1,1)模型来描述收益率的波动情况.结果表明,我国股票市场的风险较大,有较强的羊群效应和投机性;从信息冲击曲线可以看出,利好消息对价格波动的影响小于利空消息对价格波动的影响.
3.3 运用拟合效果较好GARCH(1,1)模型计算95%置信水平下的上证指数的VaR和CVaR值,从VaR和CVaR值的统计特征和LR统计量,结合我国股市的投机性的特征来看,选择较保守的投资策略更为合理,即通过GARCH(1,1)-GED模型计算CVaR值来预测股市风险.
〔1〕Jorion P.Value at risk:The neWbenchmark for controlling market risk.NeWYork:McGraw-Hill Companies,Inc,1997.
〔2〕Rockafeller R.T.,U ryasev S..OptiMization of Conditional Value-at-R isk.The Journal of Risk,2000,(3):21-41.
〔3〕Rockafeller R.T.,U ryasev S..Conditional Value-at-Risk for General Loss Distributions.Journal of Banking and Finance,2001,(7):1443-1471.
〔4〕Engle R F.Autoregressive conditional heteroscedasticity With estimates of the variance of united kingdoMinflation.Econometrica,1982,(4):987-1007.
〔5〕Bollerslev T.Generalised autoregressive conditional heteroskedasticy.Journal of Econometrics,1986,(31):307-327.
〔6〕Enlge Robert,David M.Lilien and Russell P. Robins.Estimating Time Vary Risk PreMia in the TerMStructure:The ARCH-MModel.1987,55:391-406.
〔7〕Zakoian J.M.Threshold Heteroskedastic Modles.Journal of EconoMic DynaMics and Control,1994,18:931-944.
〔8〕Nelson D.B..Conditional heteroscedasticity in asset returns:a neWapproach.Econometrica,1991,(2):347-370.
〔9〕Ding Zhuangxin,C.W.J,Granger and R.f.Engle.A long Memory Property of Stock Market Returns and a NeWModle.Journal of Empirical Finance,1993,1:83-106.
〔10〕Kupiec P..Techniques for verifying the accuracy of risk measurement models.Journal of Derivatives,1995,(3):73-84.
F830.91
A
1673-260X(2013)07-0040-05
