模糊理论与空间义量词认知

孙肇春

（广东外语外贸大学，广东 广州 510420）

1 引言

量词是汉语的重要词类，是汉藏语系诸语言的主要特色之一.“量”是人们认知世界、把握世界和表述世界的重要范畴.在客观世界中，事物性状等无不含有“量”的因素.虽然有的语言中没有量词，但是都会通过一定的方式表达量关系，只是语言表现的方式有所不同.量并不是汉语特有的范畴，而是在独立语、屈折语和黏着语这三大类语言类型中普遍存在的语言范畴.本文用模糊理论（Fuzzy Theory）解释汉语空间义量词在人脑中的认知规律.

2 模糊理论

2.1 什么是模糊理论？

模糊理论是美国加利福尼亚大学自动控制专家柴德教授的论文“模糊集合理论”（Fuzzy Set Theory）（Zadeh,L.A 1965:338-353）的基础上发展起来的，是描述和处理现实世界模糊数量关系的数学分支.经典数学中概念的特点是：对于某一具体对象或是符合这个概念，或是不符合这个概念，二者必居其一且仅居其一.这种概念一般称之为清晰的或分明的概念，表示这个概念的集合称之为清晰集合或分明集合.但是，在日常生活中所遇到的概念并不都是清晰的，还存在着大量不清晰的概念.所谓不清晰概念，是指存在着那样的对象，人们无法说它绝对符合或绝对不符合某概念.对用来表示这个概念的集合来说，就是在论域U中存在着并非绝对属于或绝对不属于某集合A的元素u.模糊现象和模糊概念无处不在，如自然语言中的“年轻人”，“高个子”，“多云天气”没有明确的内涵和外延，因而是不明确的和模糊的.随着信息时代的到来，精确性与模糊性的矛盾更加突出.一方面，各门学科迫切要求数学化、定量化.但是科学的深化从另一方面讲就意味着研究对象的复杂化，而越复杂的东西就越难以精确化.大量事实表明，许多事物过分追求精确反倒更模糊，适当地模糊反而可以达到精确的目的（梁保松，曹殿立，2007:16）.

2.2 从二值逻辑到模糊逻辑

二值逻辑（two-valued logic），或称二律背反、矛盾律、排中律，是把一件事物看成是两个对立面，如：正与反、矛与盾、敌与我.在经典数学里，确定一个元素与某一集合的关系时，只能有两种回答，“是”与“不是”.但是人们发现，现实生活中还有另一类模糊性现象不能这样描述，比如，“高个子”，“老年人”，等.假如规定身高1米8算是高个子，那么1米79算不算高个子呢？照经典数学的观点来看是不算的，这确实是有悖于情理.再以“秃头悖论”为例：以N表示一个人的头发根数，N=0的人显然都是秃头.假若有N根头发的人称为秃头，则比N根头发只多一根的人（N+1）也必然是秃头.由数学归纳法，则可推出一切人都是秃头.这个悖论的出现，也就说明不能把一个由普通集合刻划的推理方法应用到任何集合上去，特别是那些外延不分明的概念和事物.或者说，二值逻辑不能到处运用，量变到质变的差别是不能用“是”与“非”来刻划的.从差异的一方到差异的另一方，中间经历了一个差异的过渡，处于中间过渡状态中的事物显示出亦彼亦此或非彼非此性质，由这种亦此亦彼所引起的外延判断和划分上的不确定性，就必须要用多值逻辑来表达.

柴德的《模糊集合理论》把经典集合中由二值逻辑规定的特征函数重新定义为集合上隶属函数：设一集合为A，其隶属函数在A中任一元素x上的值 A（x）可以是[0,1]，也可以是[0,1]之间的任意实数.A（x）称为x对集合A的隶属程度，这样描述的集合称为模糊子集，也称为不分明集或弗晰集.当A（x）对所有x∈A只取0和1时，A就是一个经典集合.故模糊集合是经典集合概念的推广，是人们对客观事物深层的认识.这样人们就不能再把世界简单地一分为二看成A和非A，矛和盾.一个命题不但可取真、假两值，而且可取三值、四值，乃至多值，否定了“是”，不一定得到“不是”；肯定了“非”，不一定就否定了“是”.对命题的多值逻辑关系的研究，人们称之为多值逻辑（multi-valued logic）.随着神经科学和脑科学的发展，科学家们认识到用来构建大脑和计算机的基本元件的活动行为是完全不同的.计算机的基本元件是晶体管，大脑的基本元件叫做“突触”.生物学家们认为，晶体管和突触的一个首要差别是，突触不仅具备计算机使用的开、关两种状态，突触能够部分的开、部分的关.所以突触除了有相当于二值逻辑的0和1两种状态以外，还可能有中间值，比如十分之一，十分之三，等等.用模糊逻辑的语言来说，真值不仅可以取0、1两种极端情形，还可以取0、1之间的中间值.因此，与二值逻辑相比，多值逻辑更加接近人脑的逻辑思维方式.

3 量词的认知

3.1 量词研究方法的嬗变

汉语量词的系统研究在方法论上经历了三个主要时期（宗守云，2008：69-73）：一是以语义为取向的量词类别研究.这一阶段重视事实的描写和挖掘，为量词的进一步研究打下了坚实的基础.这一时期的研究以王力（1985）、吕叔湘（1979）、高名凯（1986）为代表.二是以关系为取向的量词选择研究.以关系为取向的量词研究对量词和其他词类的句法关系和语义关系进行了深入细致的描写与分析，建立了汉语量词的描写体系.这一时期的研究以陆俭明（1987：53-72）、邵敬敏（1993：181-188）、邢福义（1993：36-56）为代表.三是以解释为取向的量词认知研究.以解释为取向的量词认知研究对汉语量词设立和运用的机制及其范畴化过程进行了深入的探索.这一研究的理论来源是有关范畴划分的理论.这一时期的研究以Tai（1990）、石毓智（2001：34-41）为代表.石毓智运用数理逻辑研究量词在空间中的维数关系，石毓智指出，量词与名词的搭配不是随意的，而是由所修饰名词指示的事物的各个维度之间的比例关系决定的.这种观点从数理逻辑和认知科学角度分析名词和量词的选择关系，具有突破性，在认知的理论层面，给量词与名词的搭配一个简单又一致的解释.这个理论对量词的认知基础分析较为深刻，为我们研究量词提供了一个新的视野.

3.2 量词的空间属性

量与空间看似两个完全不同的范畴，但量词的本身是具有空间性的，对量词的空间认知反映出了一个民族对量的认识的范畴.量的特征存在于客观事物的本体之中，而客观事物都具有空间性，或称延展性（extension）（Decartes,Translated in 1996），这样量就表现为事物的空间量.事物空间上的长度、宽度、高度等都与事物的数量的多少有关系.空间量就是事物量的性质，空间的量特征是事物的存在与表达的主要特征.李秀（2004）认为许多量词都具有一定的外形特征，这种外形的特征是量词产生时与生俱来的，并在使用过程中逐渐被认可了的，这就要求量词与它所修饰限定的名词之间具有相同、相近或相似的外形特征.这种要求也体现在语义层面上.这类量词大致可以分为点类、条类、面类和体类等，由于人们的认识是从具体到抽象的，也就是人们对抽象的事物的认识是来源于具体并从具体开始的，抽象事物也因此有了具体的量化认识，这种认识符合人们认知结构与思维模式.

3.3 空间义量词的认知模式

大多量词都具有空间意义.邵敬敏（1993）把专用量词分为两大类：外形特征类量词和非外形特征类量词.外形特征类量词具有明显的空间义，如：点、粒、颖、滴、线、丝、条、枝、块、环、丛、口、等，这些量词几乎都是由名词转化而来，因此仍然保留着空间义.另外，还有一些量词由动词转化而来，如：串、堆、抽、担、把、卷、摄、捧、包、等，作为量词，它们强调该动作所导致的空间状态，因此它们也具有空间义.邵敬敏还进一步把形状量词细分为点状、线状、面状、体状量词：

点状形状量词：粒、滴、丸；

线状形状：道、段、根、股、管、行、截、节、列、揍、络、排、丝、条、线、支；

面状形状量词：层、面、片、张；

体状形状量词：块、团、包、堆；

上述量词表达物体的空间特性，它们中有大量的名词借用为量词的临时量词，而名词借用为量词，与原始思维中的数量观念有关.在度量衡方面，空间概念的形成往往先于重量、面积的概念，这是因为把农作物分成堆以及用容器盛舀物品是最方便易行的办法.农作物中固体东西往往以大小不等的箩、斗、桶计，而酒、油等液体以碗、罐、瓶计，很少以重量计（胡起望，1982）.这种心理机制一直影响着我们，如我们买瓶装或罐装的饮料或食品时，抛开价钱因素不算，主要考虑的是瓶罐体积的大小，很少去注意瓶罐上标注的饮料食品的实际重量.不仅如此，利用一种事物的空间来表示另一种事物的数量一直保留并使用着.如：一扁担的肉包子、一车的人、一抽屉书.由于名词具有实体性，不考虑数词的限制，临时量词如何表示事物的量呢？那就是空间被占据多大，就表示量有多大（朱晓军，2008：98）.

空间义量词表达事物的空间范畴，因此，我们可以把“空间”作为语言变量，不同的量词所表达的空间义就是这个变量的不同的值.为了直观，我们用XYZ（分别表示长、宽、高）来表示一个三维空间.

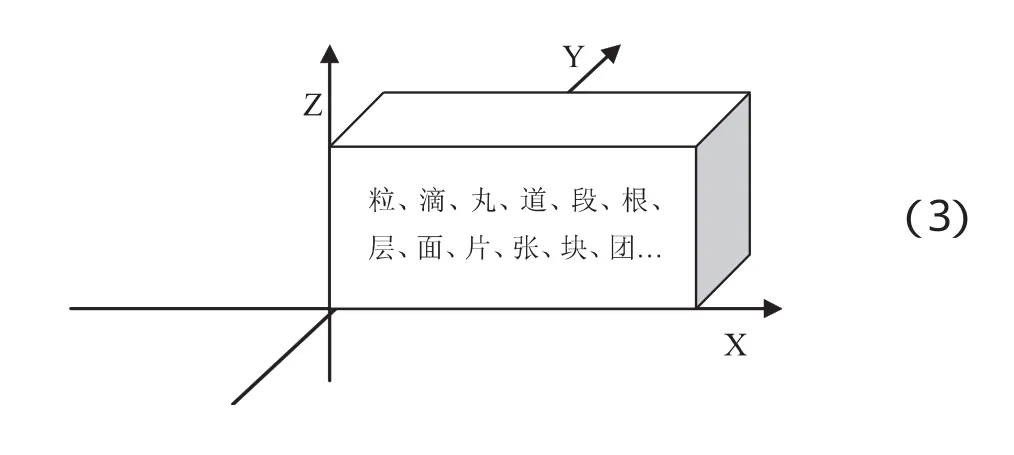
在三维空间XYZ中，我们可以对空间变量取不同的值，它们可以是“粒、滴、丸、道、段、根、层、面、片、张、块、团”等.每一个值都可以看成论域U(XYZ)的模糊子集.一个物体选择什么样的量词取决于该物体形态特征在模糊子集中的隶属函数.一个物体的形态特征在某一量词模糊子集中的隶属函数值A(x)总是在[0,1]区间.如超出这个区间，该物体形态特征则属于另一个量词模糊子集.下面我们以空间义量词“片”和“块”为例，用隶属函数式解释人脑如何对量词进行认知.

根据《现代汉语八百词》，量词“片”用于表示“平而薄的东西”，如：一片树叶、几片花瓣、一片瓦、两片面包、等.“片”也可以用于表示面积、范围较大的东西，多指地面、水面，如：一片草地、一片树林、一片庄稼（吕叔湘，1999：429）.量词“块”用于表示块状或某些片状的东西，如：一块砖（肥皂、石头、）、两块糖（肉、蛋糕、小骨头）、几块木板（木料、铁板、匾）（吕叔湘，1999：340）.从以上的解释我们可以看出，量词“片”修饰的名词通常都是比较薄的物体，而量词“块”修饰的物体通常具有一定的厚度.两个量词之间的差别主要与物体的厚度（Z）相关.例如，“一片面包”比“一块面包”的厚度要小.同时，我们也注意到，这两个量词都可以修饰片状的东西，例如：某一特定厚度的木板，我们既可以说一片木板，也可以说一块木板.但这种重叠仅限于某一特定范围，超出这一范围，“片”和“块”的选择还是非常分明的.根据人脑对空间的认知和我们的专家知识，我们可以提出这样的假设：在某一物体的长和宽（X,Y）为1的情况下，其高度（Z）≤0.3时，该物体属于量词“片”的模糊子集，即：“片”的隶属函数为1.如该物体的高度（Z）＞0.5时，该物体不属于量词“片”的模糊子集，即：“片”的隶属函数为0.而当物体的高度（Z）值处于0.3-0.5之间时，该物体属于模糊子集“片”的隶属函数为0＜A(x)＜1.我们可以用函数式（4）表示模糊子集“片”的隶属函数关系.

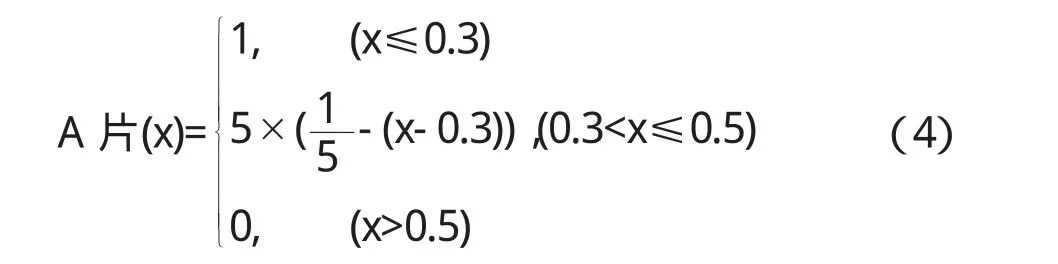
由函数式（4）我们可以计算出，当某一物体长、宽为1，高度/厚度为0.4时，量词“片”的隶属度是0.5（A片(x)=0.5），即：该物体可用量词“片”修饰的可能性为50%；如该物体高度/厚度为0.45时，量词“片”的隶属度是 0.25（A片(x)=0.25），即：该物体可用量词“片”修饰的可能性为25%；当该物体高度/厚度为0.5时，量词“片”的隶属度是0（A片(x)=0），即：该物体可用量词“片”修饰的可能性为0.同样，我们可以列出物体属于量词“块”的隶属函数关系.

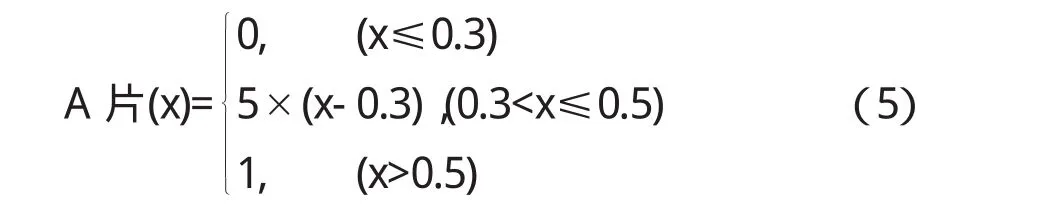
假设某一物体长、宽（X,Y）为1，根据函数式（5），当一个物体的高度/厚度Z≤0.3时，量词“块”的隶属函数是0（B块(x)=0），即：该物体不属于“块”的模糊子集.当一个物体的高度/厚度Z＞0.5时，量词“块”的隶属函数是 1（B块(x)=1），即：该物体属于“块”的模糊子集.当某物体的高度/厚度为0.4时，“块”的隶属函数值是0.5（B块(x)=0.5），即：该物体可用量词“块”修饰的可能性为50%；如该物体高度/厚度为0.45时，量词“块”的隶属度是 0.75（B块(x)=0.75），即：该物体可用量词“块”修饰的可能性为75%.进一步分析我们可以看到，在函数式（4）中，量词“片”的隶属函数与物体的高度/厚度呈反比关系，物体的高度/厚度越大，函数值越小.这意味着随着物体的高度/厚度的增加，该物体可用量词“片”修饰的可能性越来越小.在函数式（5）中，量词“块”的隶属函数与物体的高度/厚度呈正比关系，物体的高度/厚度越大，函数值越大.这意味着随着物体的高度/厚度的增加，该物体可用量词“块”修饰的可能性越来越大.

函数式（4）、（5）刻画了人类大脑对于空间义量词“片”和“块”的认知模式.一个物体选择什么样的量词取决于该物体的空间特征.只有充分认识了空间概念，人脑才开始对量词具有初步认知.根据对4-6岁普通话儿童量词习得研究，4岁儿童只掌握4个左右的量词，而随着年龄的增长，到6岁时，掌握的量词增加大9个左右，错误量也大大减少（方富熹，1985：384-392）.这说明量词的认知不是单纯的语言问题，它与人脑整体认知能力的发展具有紧密联系.

4 小结

本文运用模糊数学的方法揭示了汉语空间义量词的认知模式.量词表达事物的量，而量需要占用空间，因此我们认为，汉语量词的实质是表达物体空间特征.量词的认知过程实际上就是范畴化过程（Harnad 2003）.物体选择什么样的量词取决于该物体属于论域中的量词模糊子集.当然，我们的研究也有不足之处.毕竟，语言不是数学，不可能象数学那样严格.由于方言的差异，量词在不同的方言中使用习惯具有极大的差异.我们的目的在于用数理逻辑的方法解释人类对语言的认知过程，从而发现其中的内在规律.

〔1〕宗守云.汉语量词研究方法论的嬗变[J].扬州大学学报（人文科学版),2008(1):69-73.

〔2〕王力.中国现代文法[M].北京：商务印书馆，1985.

〔3〕吕叔湘.汉语语法分析问题[M].北京：商务印书馆，1979；现代汉语八百词[M].增定本.北京：商务印书馆，1999.349，420.

〔4〕高名凯.汉语语法论[M].北京：商务印书馆，1986.

〔5〕陆俭明.数量词中间插入形容词情况考察[J].语言教学与研究，1987(4):53-72.

〔6〕邢福义.现代汉语数量词系统中的“半”和“双”[J].语言教学与研究，1993(4):36-56.

〔7〕石毓智.表物体形状的量词的认知基础[J].语言教学与研究，2001(1):34-41.

〔8〕梁保松，曹殿立.模糊数学及其应用[M].北京：科学出版社，2007.16.

〔9〕刘应明，任平.模糊数学[M].上海：上海教育出版社，1988.74.

〔10〕李秀.外形特征类量词的语义辨析及发展趋势[J].内蒙古师范大学学报，2004(1).

〔11〕张志公.现代汉语 [M].人民教育出版社，1982.180.

〔12〕朱晓军.空间范畴的语义认知研究[D].华东师范大学，2008.96.

〔13〕方富熹.4-6岁儿童掌握汉语量词水平的实验研究[J].心理学报，1985（4）：384-392.

〔14〕Zadeh,L.A..Fuzzy Sets,Infl and Control[J].1965(8):338–353.

〔15〕Tai James H-Y&Lianqing Wang,1990,A semantic study of the classifierTiao,Journal of the Chinese Language Teacher Association[J].25(1):35-36.

〔16〕Descartes René,Meditations on First Philosophy,translated by John Cottingham[M].Cambridge:Cambridge University Press,1996.

〔17〕Harnad,Steven,2003,To Cognize isto Categorize:Cognition is Categorization[P].Paper presented at UqaM Summer Institute in Cognitive Sciences on Categorisation,Center de neuroscience de la cognition,Canada.