数学问题表征与数学问题图式

罗 奇，唐剑岚

（1．桂林师范高等专科学校 数学与计算机科学系，广西 桂林 541002；2．广西师范大学 数学科学学院，广西 桂林 541004）

有关数学问题解决国内外已有了大量的研究[1～4]．最初对数学问题解决的研究主要集中在数学问题解决过程及模式的建构和应用中，近年来越来越多的学者关注于数学问题解决内在机制的研究，尤其侧重于问题理解阶段的表征、图式理论在解题中的应用、问题解决各阶段的策略以及解题过程的元认知分析等．实践领域中也出现了应用性研究，如解题策略的训练，元认知能力的培养等．可见，对数学问题解决的心理学研究已比较全面和丰富，很多理论得以继承和发展．

但如何将问题表征、图式构建与个体思维形成的主要途径——数学解题联系起来，在数学解题教与学中提高解题能力的研究还需进一步验证和探讨．因为，一方面表征是问题解决的一个中心环节，要想使问题得以解决，主体必须合理地表征问题，其对问题的表征如何，极大地影响着问题解决的难易程度[5]．另一方面数学问题求解又具有内容的抽象性、结构的严谨性、推理的逻辑性等特点，这与图式理论表现出极大的相容性．有鉴于此，这里对数学问题表征和数学问题图式及其关系进行了探讨．不断试误，主体会不断修正自己对问题的表征，使之更为准确适宜，而问题解决过程中顿悟现象的出现是由于主体找到了适宜的问题表征[10]．

下面通过对师范数学专业二年级学生解题过程与解题时教师询问窥视表征对学生数学解题作用进行个案分析．（以下学生成绩以高考数学成绩为评定标准）

例1t为何值时，不等式恰好有一个解．

被试 A（成绩差）：我将不等式变形为x2+9≥tx≥x2+1后就不知道怎样入手求解了．

1 数学问题表征

的图像，注意到问题可以看成：t取何值时，函数只有一个值落在[-3, 5]区间内．因为该函数图像是开口向下的抛物线，如果此抛物线的顶点在直线y=-3上方，则函数取值有无穷多个落在区间[-3, 5]中；如果此抛物线顶点在直线y=-3下方，则函数值都小于-3，函数值全部不落在区间[-3, 5]中；当且仅当此抛物线的顶点落在直线y=-3上时，函数取值只有一个落在[-3, 5]．即有一个函数值等于-3，其余的函数值均小于-3．从而得出

1.1 数学问题表征及对问题解决的作用

问题表征指形成问题空间，包括明确问题的初始状态、目标状态及允许的操作[6]．问题表征形式上可以分成两种[7]：一种是外在表征，即将问题以文字、数式、图表、模型和实验等具体的东西表示出来；另一种是内在表征，即问题在人脑中的思考．两者相互关联，内在表征是外在表征的基础，外在表征是内在表征的具体化和外显化．

在数学问题解决中，表征问题是解决问题的前提条件，主体若要理解某个数学结构，就必须在这个数学结构与一个更易理解的数学结构之间建立一个映射，而表征就是这个映射过程[8]．如何对问题情境进行准确、有效地表征往往是顺利解决问题的关键，因为问题难度上的差异一方面源于问题自身结构，另一方面源于主体在表征问题方式上的不同．有研究表明问题的适当表征与问题的成功解决之间存在正相关[9]，不当表征与解题成绩呈负相关[4]．同时在解题过程中，主体对问题的表征不是静止不变的，随着对问题情境理解的

可见，被试 A无法表征问题，问题也就无法求解；被试 B采用代数方式来表征问题，导致解决问题过程非常复杂，难以进行；被试C首先是采用与被试B类似方法表征问题，发现难于求解，修正表征，采用几何方式表征问题和求解，过程既直观又简捷．

另外，问题表征方式具有多样性．Markman与Dietrich[11]认为，不同类型的问题表征方式适合于不同心理加工过程．适当的表征把对问题解决最有价值的重要成分和结构关系放到一个突出的位置上．Simon[12]也指出，有时按照常规方式表征的问题难以求解，但若换了一个角度来表征同一个问题，问题就迎刃而解了．

如果用三角化简的方法尝试证明结论，则比较困难、繁杂．注意到0≤sinα, sinβ, sinγ≤1和结论的结构形式，联想到相互独立事件的概率公式，则问题易解．

1.2 数学问题表征的依据和形式

数学问题表征的依据一是问题的客观方面，即要求在对问题转化为数学模型时要切实依据问题的文字、图表，以及它们之间的关系；二是主体的认知结构，即主体已有的数学知识、解题经验、思想方法、策略等．

数学问题表征按表征的深入层次可分为：字面表征，真实情景表征，数学表征．按照表征的方式，则可分为：言语表征、图像表征、方法表征和原理表征．方法表征是用程序性的知识来表达对问题的求解，数学表征和原理表征类似，都是用与问题情景紧密相联的数学规律来表征问题．

当然对问题的表征有时是不同的表征方式的同时运用．可以注意到优生在建立字面表征的同时便明显地开始建立真实情景表征，以至读完题就能利用数学规律得到数学表征，进而求得问题结果．另外，优生的知识具有简约性、结构性，他们往往以知识组块的形式提取知识，同时其知识结构中还包含了应用知识的程序性知识和策略性知识[13]，这些都影响着对问题的表征．

至于对复杂问题的表征，往往需要多元表征的参与．大量研究表明，多元表征对数学问题解决过程与结果有直接或间接的影响．而多元表征的每种表征都有自己的优势和不足，不同偏好的主体在问题解决时，运用不同的表征．多元表征的恰当运用在一定程度上降低数学理解的难度，而且使得数学更具吸引力和趣味，同时各种表征间的转换与转译是解决问题的关键[8]．

2 数学问题图式

2.1 数学问题图式的内容及分类

图式理论是一种关于人的知识是怎样表征出来，以及关于知识的表征如何以特有的方式有利于知识的应用的理论．按照该理论，人脑中保存的一切知识都能分成单元、构成组块和组成系统，这些单元、组块和系统就是图式[14]．

数学问题图式可以看成数学问题解决过程的图式，它包含两部分信息：其一是关于它所对应的某类问题的特征描述，其二是这类问题的解决的知识、方法和程序．数学问题图式具有灵活性、适应性、强迁移性和概括性．因而一旦激活一个问题图式即可自动通达并执行相应的解题程序．所以问题图式的形成以及数量和质量是解题能力的标志．数学问题图式围绕数学概念和规律组织，包含陈述性知识、程序性知识、策略性知识及典型的问题情景特征等．主体在数学问题求解时明确问题、构建和选用方法等都要应用图式．

根据数学问题求解过程，将数学问题图式分为问题情境图式、问题解答图式和问题反思图式．问题情境图式是对数学问题的情境环境的认知．已有的情境图式帮助主体识别数学问题环境，并指导主体采取相应的行动来实现目标．不同的问题带给主体不同的情境图式，同一主体对同一个问题也会产生不同的情境图式，所建构的情境图式的优劣对解决问题具有重要意义．问题解答图式是指解题时采取的策略、方法等，比如分析问题策略、推理判断策略，以及解题的具体方法．如数学归纳法、关系映射反演法、构造方法、类比方法、分类讨论方法等．反思图式是对数学问题认识及解决过程中或解决过程后的相关问题的认知，如对策略、程序等认知过程的反思．反思是数学解题中的重要一环，提高数学问题求解能力离不开反思图式．

2.2 数学问题图式形成及对问题解决的作用

学生在数学问题解决中常出现“听得懂，看得会，做不对”，这说明从知识到能力，解题原理到问题解决，还有一个不可或缺的心理历程，那就是形成合理的知识组块、形成问题解决的图式．图式是建立在每一个具体问题解决后在头脑形成的“模板”基础上，由于同类问题有不同的变式，因此当人们大量地遇到不同变式的同类问题时，每解决一次，头脑中的“模板”也随之得到相应加强或改变．随着解决问题的增多，“模板”逐渐演化成代表一类问题的概括性内部表征即图式．

数学问题图式对于数学问题解决具有重要作用[15]，一方面，在数学问题解决过程中，数学问题图式不仅影响着主体对问题的感知和理解，还影响着问题解决策略、方法的获得与使用．首先，当处于问题情境中，主体对外界信息的选择与加工需要过去知识经验的参与；其次，当面对新的刺激信息，要赋予新信息一定的意义时，主体必须把其纳入已有的数学问题图式中，相关图式的激活能帮助主体迅速理解问题的本质，而数学问题图式所提供的相关知识经验也可弥补问题情境中所缺失或隐藏的信息，使得主体对新信息的组织和理解更为合理有效，从而提高问题解决的效率；再次，当主体确定了问题的性质，对问题有了正确的理解，这时仍需要启动正确的数学问题图式才能获取解决问题的有效方法．另一方面，数学问题图式有时候也会阻碍问题的顺利解决，一般来说，它在3个方面干扰问题的解决：第一，可能造成大量信息的丧失，由于图式对信息有过滤和筛选的作用，这样许多信息就有可能被过滤掉，从而影响了对信息的全面获取；第二，图式常难以去除，图式本身可以构成定势，当主体形成某种数学问题图式后，往往倾向于用这种固有图式去组织和同化信息，这会阻碍新的更为合适的图式的形成；第三，可能使用错误的图式，误导问题解决，一旦激活了错误的数学问题图式，主体对问题的理解和加工均在一个错误的框架里进行，必然导致问题解决的失败．

下面再次对师范数学专业二年级学生解题过程进行个案分析．

例3 已知z∈C，且满足，，求复数z．

被试D（成绩差）：看到有辐角的题，我感觉求解困难．转化成代数形式；令代入已知得：

被试 E（成绩中）：已知辐角主值，立刻想到复数的三

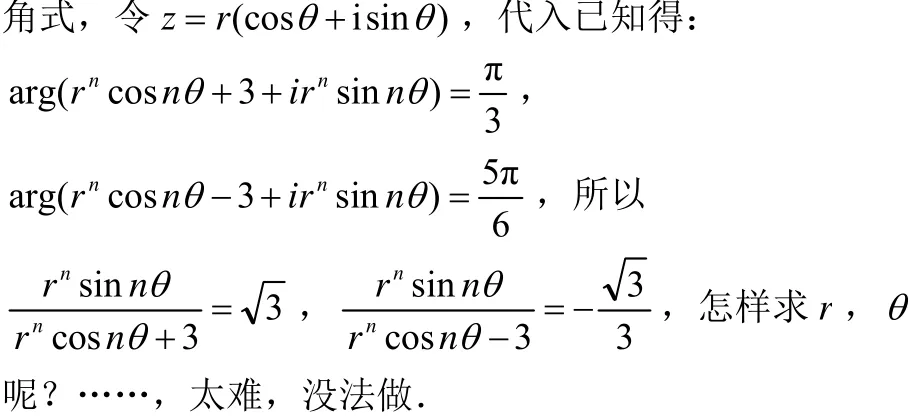
被试G（成绩好）：一看到题中的辐角主值，立刻想到复数的三角式，又联想到了复数zn+3，zn-3的几何意义．要想将这两部分结合起来，需建立直角坐标系．将zn+3，zn-3在坐标系中表示出来，这样就得到zn所对应的M点，这时问题变得明朗了，即利用已知条件画出图形求出zn，进而求出

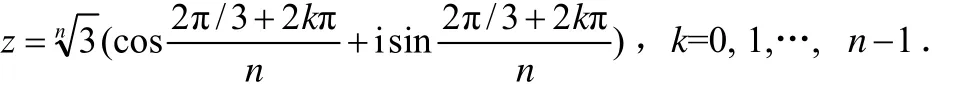
可见，被试 D在解题过程中，没有构成相关的图式，难以求解；被试 E在解题过程中，能够构建复数的三角形式图式，但zn+3，zn-3没有激活相关图式，这是造成思路受阻的主要原因；被试F在解题过程中，zn+3，zn-3没能激活复数几何意义图式，在经过代换后，才激活此图式，说明其复数几何形式图式不完整．后面受向量模的性质影响，出现错误复数性质图式，从而误导结论；被试 G在解题过程中，辐角主值激活复数三角形式图式，由zn+3，zn-3激活复数几何意义图式，然后对激活的两个图式进行分析，构造最佳拟合状态——建立直角坐标系，致使问题得以解决．

3 数学问题表征和数学问题图式的关系[16～18]

数学问题表征和数学问题图式是两个既有区别又有联系的概念，一方面，数学问题表征是数学问题图式形成的基础，也是数学问题图式应用的基础，数学问题图式的形成首先需要对问题进行正确的表征，没有对问题的正确表征就不可能有完善的问题图式，数学问题图式的激活也需要以数学问题表征为前提．另一方面，数学问题图式对于数学问题表征也具有重要意义，对一个问题进行正确的表征首先需要从长时记忆中激活相关的问题图式，并在图式的框架中对问题信息进行筛选和组织加工．没有图式的参与，问题中呈现的信息是零乱和缺乏意义的．数学问题表征时需要深化整合、灵活迁移已有的数学问题图式，对于一些陌生问题，没有直接同化当前情境的图式，数学问题表征的过程也就是尝试建立这类问题新图式的过程，如上面被试C求解例1的几何表征问题过程其实也是用函数图像求解不等式问题的图式建立过程．

下面例题说明，对问题深层结构的正确表征，更容易激活问题图式，顺利地解决问题．

例4 设α，β是关于x的方程0①的根，试证明关于x的方程的根是a，b．

题目的条件说α，β是方程①的根时，a，b处于方程系数的位置；题目的结论说a，b是方程②的根时，α，β处于方程系数的位置．因而，条件与结论之间，(α,β)与(a,b)之间都有一种对称关系，所以，条件表征为

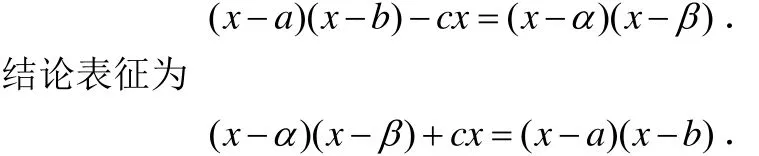
对比，只需作一步移项运算就消除了差异．

反之，图式的水平也影响到问题表征[19]．较高的图式水平能够促进问题的深层结构表征，如果一个问题的解决要求的表征复杂性越大，对知识基础的要求越多，那么该问题图式的水平就越高，并且优生通常比普通生有更高的图式水平，更善于表征问题中复杂的关系[20]．

数学问题图式的水平主要表现为主体所掌握的数学知识、思想方法、解题策略和经验的概括程度．一级水平为“一对一”图式，即把一道题及其解法作为图式．二级水平为：“典型实例”图式，即记住某类题中一道典型题的解题思路，以后遇到类似问题，就以此为例去解决．第三级为“概括特征”图式，即摒弃题的具体内容，概括了某类题的一般特征及解题思路．图式级别越高就越能够正确表征问题、求解问题．

由上可见，提高数学问题表征能力和数学问题图式水平对提高数学解题能力、完善和发展学生认知结构有较高的价值和指导意义．一方面，教师在教学中要重视数学问题表征能力的培养．为此，要注重培养学生对数学问题语意的理解和转化能力、优化学生的数学认知结构、完善学生数学问题的多元表征系统．另外，数学学习信念直接或间接地影响着问题的表征[21]，所以增强学生数学学习的信念也不可忽视．另一方面，在教学中必须有意识地构建数学问题图式．图式形成后，还须防止误用图式，要注意将正确应用该图式的情景与误用情景进行比较，以识别关键差异，并将关键差异编码作为图式的一部分．此外，图式抽象水平应该符合学生的思维发展水平．图式抽象概括时，不能局限于学生当前的思维水平，要积极推动学生的抽象思维水平的发展；但也不能单凭教师的主观愿望一味强调图式抽象，当超出学生的接受能力时，总结出来的“概括特征”图式就会变成学生记忆的负担，很难被学生灵活地用到解题活动中[3]．

[1]于文华．基于数学问题解决的模式识别研究述评[J]．数学教育学报，2012，21（3）：11-16．

[2]王林全．问题解决的有关心理活动及其思考[J]．数学教育学报，2002，11（1）：36-38．

[3]郭兆明，宋宝和，张庆林．代数应用题图式研究概述[J]．数学教育学报，2007，16（4）：20-23．

[4]徐速．数学问题解决中视觉空间表征研究的综述[J]．数学教育学报，2006，15（1）：35-38．

[5]Simon H A．人类的认知—思维的信息加工理论[M]．荆其诚译．北京：科学出版社，1986．

[6]喻平．数学教育心理学[M]．南宁：广西教育出版社，2008．

[7]何小亚．解决数学问题的心理过程分析[J]．数学教育学报，2004，13（3）：34-36．

[8]唐剑岚．国外关于数学学习中多元外在表征的研究述评[J]．数学教育学报，2008，17（1）：30-33．

[9]Novick L R, Hurley S M, Francis M. Evidence for Abstract, Schematic Knowledge of Three Spatial Diagram Representations [J]. Memory Cognition, 1999, 27(2): 288-308.

[10]Kaplan C A, Simon H A. In Search of Insight [J]. Cognitive Psychology, 1990, (32): 374-419.

[11]Markman, Dietrich. In Defense of Representation [J]. Cognitive Psychology, 2000, 40(2): 160-167．

[12]Simon H A．认知科学的一些最新进展[J]．心理学报，1991，23（2）：153-157．

[13]Larkin. Expert and Novice Performance in Solving Physics Problems [J]. Science, 1980, (208): 20.

[14]Rumelhart, D E Schemata. The Building Blocks of Cognition [A]. In: R J Spiro. Theoretical Issues in Reading Comprehension [C]. Hillsdale, NJ: Lawrence Erlbaum, 1980.

[15]徐青．场认知风格与图式水平对几何问题表征的影响[D]．河南大学，2010．

[16]Hans G K Hummel, Rob J Nadolski. Cueing for Schema Construction: Designing Problem-solving Multimedia Practicals [J]. Contemporary Educational Psychology, 2002，(27): 229–249.

[17]张夏雨，喻平．基于关系—表征复杂性模型的问题图式等级性研究[J]．数学教育学报，2009，18（4）：46．

[18]李善良．数学概念表征层次的研究[J]．数学教育学报，2005，14（4）：35–37．

[19]邓铸，姜子云．问题图式获得理论及其在教学中的应用[J]．南京师范大学学报（社会科学版），2006，（4）：111-115．

[20]张夏雨，喻平．不同学业水平学生数学问题图式的差异性研究[J]．数学教育学报，2011，20（1）：45-48．

[21]唐剑岚．学生数学认识信念的研究述评[J]．数学教育学报，2007，16（1）：29-33．