基于改进的DCT和EMD的轴承故障诊断
2013-07-20臧怀刚李清志王石云韩验龙
臧怀刚,李清志,王石云,韩验龙
(燕山大学 电气工程学院 工业计算机控制工程河北省重点实验室,河北 秦皇岛 066004)
故障特征信息提取是滚动轴承故障诊断中最关键的问题之一[1-3]。以快速Fourier变换为核心的传统频谱分析方法在平稳信号处理的特征提取中发挥了重要作用,但Fourier变换不能处理非平稳信号。小波变换具有多分辨分析的特点,能够聚焦到信号的任意细节进行多分辨率的时频分析[4],同时提供信号在时域和频域的局部化信息,但其本质是窗口可调的Fourier变换,由于小波基长度有限,因此在对信号进行时频分析时,会产生能量泄漏[5]。
经验模态分解(Empirical Mode Decomposition,EMD)是一种基于信号局部特征的信号处理方法,可得到使瞬时频率有意义的时间序列——内禀模态函数(Intrinsic Mode Function,IMF),特别适合非线性、非平稳信号的分析处理,并获得表达信号特征的信息[6-7]。文献[8]将EMD和局部Hilbert能量谱应用于轴承故障诊断中,文献[9]将EMD与SVM相结合进行轴承故障包络谱诊断,文献[10]提出基于EMD的多尺度形态学解调方法。
虽然近年来不少学者尝试使用EMD来进行轴承的故障诊断,但EMD分解之前的噪声处理还需要进一步完善。因此,研究了离散余弦变换(Discrete Cosine Transform,DCT)算法并提出了改进的DCT和EMD相结合的轴承故障诊断方法。
1 DCT算法
1.1 定义
DCT有多种定义方式,最常用的定义方式为
(1)
(2)
式中:f(x)为时域中的N点序列,x=0,1,2,…,N-1;F(k)为DCT的第k个变换系数,k为广义频率变换量,k=1,2,3,…,N-1。
DCT的反变换IDCT定义为
(3)
由于DCT具有强大的“能量集中性”,经常被用于信号处理和图像处理,它的每个变换系数都对应一定的时长,通过检测各个时窗内信号幅值的变化来捕捉信号的变化情况,而不是去捕捉与噪声统一数量级的信号突变,因此对噪声不敏感,非常适用于故障的在线检测与诊断。
1.2 阈值选择
当有用信号淹没在强背景噪声中时,噪声信号包含了信号中的主要能量,经DCT处理后,大部分噪声能量反映在高频系数上,故障信号能量则主要集中在低频系数。通过对能量较大的高频系数和能量较小的低频系数进行阈值处理,再通过IDCT重构信号,能够有效去除噪声,提取出包含在噪声中的微弱故障信息。
改进的DCT算法的具体过程如下:
(1)对采集到的信号进行DCT处理,得到DCT系数F(k);
(2)求所有系数的绝对值G(k),找出绝对值的最大值M;
(3)如果G(k)>αM或G(k)<βM,则F(k)=0;否则F(k)保持不变。其中α和β分别定义为高频阈值系数和低频阈值系数,0<β<α<1;
(4)利用处理过的DCT系数进行IDCT,重构原始信号。
2 EMD基本原理
EMD方法将一个复杂的信号分解为若干个IMF之和,其基于以下2个假设:(1)任何复杂的信号都是由一些不同的IMF组成,每个IMF不论是线性、非线性或非平稳的,都具有相同数量的极值点和过零点,在相邻的2个过零点之间只有1个极值点,而且上、下包络线关于时间轴局部对称,任何2个模态之间是相互独立的;(2)任何时候,一个信号都可以包含许多IMF,如果模态函数相互重叠,便形成复杂信号。在此假设的基础上,可以采用EMD方法通过以下步骤对任何信号x(t)进行分解。
(1)初始化r0=x(t),i=1;
(2)得到第i个imf:
(a)初始化h0=ri-1(t),j=1;
(b)找出hj-1(t)的局部极值点;
(c)对hj-1(t)的极大和极小值点分别进行3次样条函数插值,形成上下包络线;
(d)计算上下包络线的平均值mj-1(t);
(e)hj(t)=hj-1(t)-mj-1(t);
(f)若hj(t)是IMF函数,则imfi(t)=hj(t);否则,j=j+1,转到(b);
(3)ri(t)=ri-1(t)-imfi(t);
(4)如果ri(t)的极值点数仍多于2个,则i=i+1,转到(2);否则,分解结束。x(t)为原信号序列,rn(t)为残余分量,代表信号的平均趋势。
算法最后可得到
(4)
理论上讲,EMD得到的都是IMF,但在实际计算过程中,采用了近似处理,没有严格按照IMF的条件判别,不能完全保证IMF的物理意义,个别IMF中会出现模态混叠或者伪IMF,造成故障误判。
3 改进的DCT-EMD算法
DCT与EMD相结合的算法过程如下:
(1)对采集到的信号x(t)进行DCT处理,得到DCT系数;
(2)设定α和β的值,利用阈值处理方法,去除能量较大的高频系数和能量较小的低频系数,将处理过的DCT系数进行IDCT,得到重构信号x′(t);
(3)对重构信号x′(t)进行EMD分解,得到多个IMF和残余分量r(t);
(4)对各个IMF求瞬时频率,查找故障特征频率所对应的IMF;
(5)对故障特征频率所对应的IMF求取频谱图;
(6)根据频谱图显示的故障特征频率判断故障类型。
4 应用分析
以文献[11]数据为例,选用外圈固定,内圈随轴转动的6205-2RS SKF型深沟球轴承。在内圈采用电火花技术加工出直径为0.355 6 mm,深度为0.279 4 mm的故障点。在转速为1 774 r/min,负载为735.5 W,采样频率为12 kHz的情况下,采集2 400个点的故障信号,时域波形如图1所示。
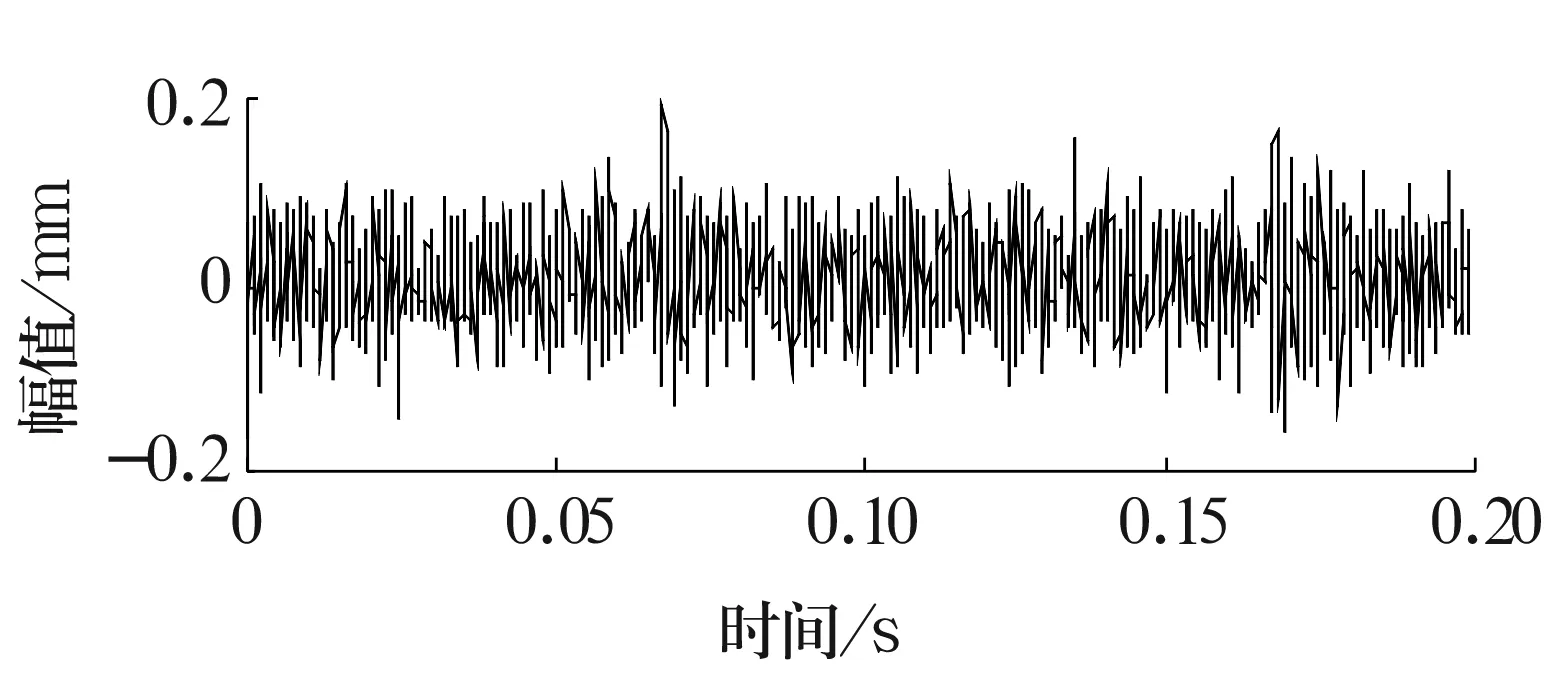
图1 故障信号时域波形
经计算可知,内圈故障频率为160.1 Hz。对故障信号直接进行EMD处理的结果如图2所示。

图2 故障信号直接EMD的结果
由图可知,直接进行EMD产生了太多的imf,造成了模态混叠,无法准确提取故障信号。经多次试验发现取α=0.88,β=0.38时,既能有效去除噪声,又能消除各频率间的干扰,应用DCT-EMD处理的结果如图3所示。

图3 故障信号进行改进的DCT-EMD结果
对比图2和图3可知,改进方法后,imf数量下降,幅值减小,信号的信噪比大幅度提高,有效减少了EMD运算次数。对图3中除了残余分量外的所有imf求取瞬时频率,结果如图4所示。
由于计算所得的内圈故障频率为160.1 Hz,查看图4可知故障频率包含在imf4所对应的频段内。对imf4做频谱变换和Hilbert-Huang谱分析,结果如图5和图6所示。
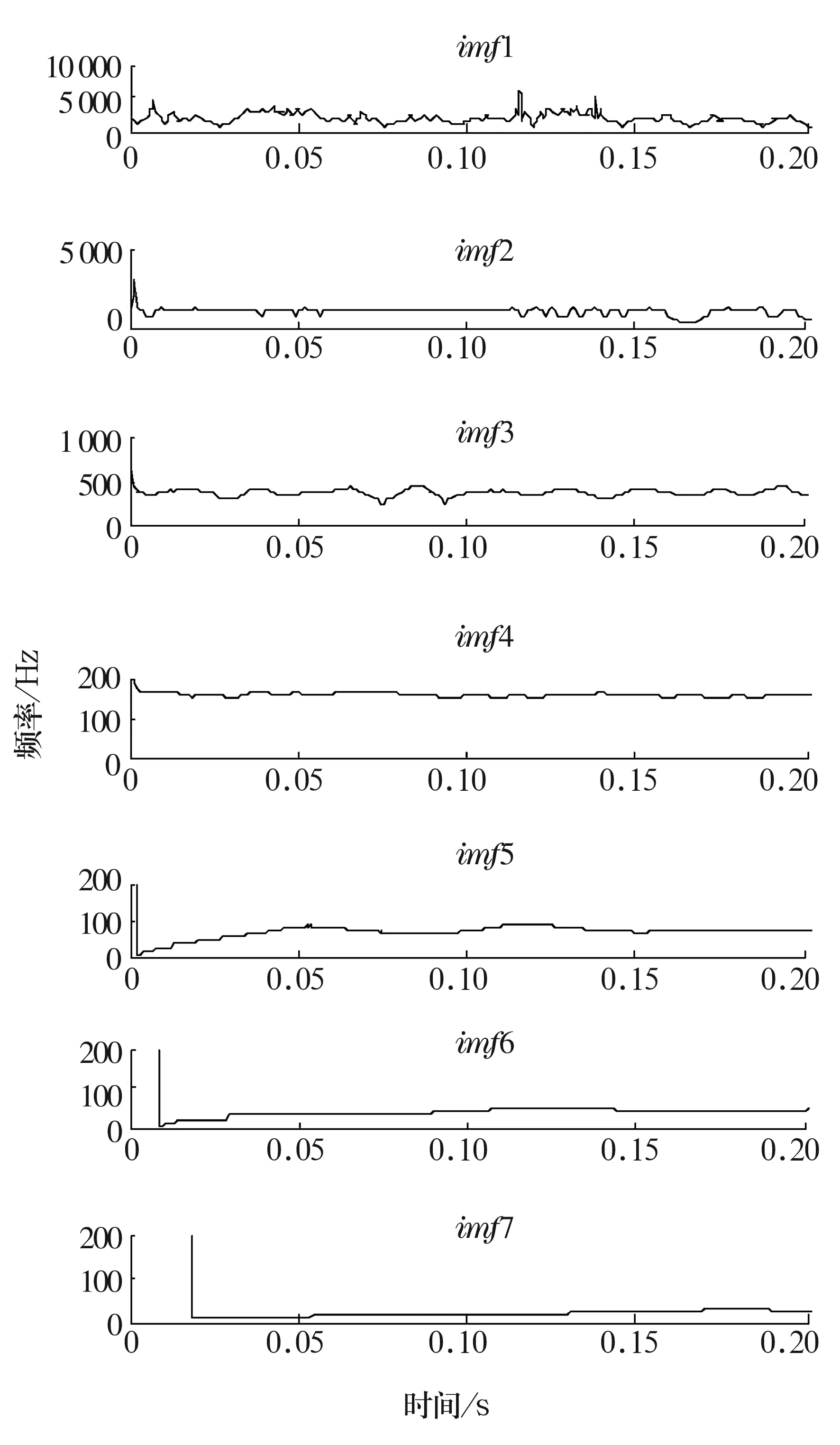
图4 imf1~imf7的瞬时频率
由图5和图6可以清晰看到内圈故障频率,出现误差的原因是:计算公式是针对内圈、外圈有一处剥落坑的情况从理论上推导出来的,而实际轴承的各几何尺寸会有误差,加上轴承安装后的变形,使计算频率与实际的特征频率有误差。

图5 imf4的频谱图

图6 imf4的Hilbert-Huang谱
5 结束语
改进的DCT-EMD方法在实际轴承故障诊断中的应用结果表明,其能够有效去除噪声,减小噪声对EMD过程的影响,同时减少了EMD的运算量,提高了信噪比,准确地提取出了轴承故障特征信息,对轴承故障做出了准确诊断,为轴承故障诊断提供了一种新方法。
