中介轴承动态特性分析
2013-07-20郭向东王燕霜
郭向东,王燕霜
(1.洛阳轴研科技股份有限公司 轨道交通轴承事业部,河南 洛阳 471039;2.河南科技大学机电工程学院,河南 洛阳 471003)
现代航空发动机主轴轴系多采用双转子结构,即将低压转子和高压转子形成机械耦合,而连接低压转子和高压转子的轴承为中介轴承[1-2]。当今航空发动机追求大推重比,从而要求主轴轴承在更高的dm·N值下工作[3]。随着dm·N值的提高,将带来中介轴承保持架和滚子的打滑、接触表面损伤和保持架不稳定等一系列问题[4-5],造成轴承寿命的降低。可见,轴承动态特性直接决定了中介轴承的寿命。所以,对中介轴承进行动态特性分析具有重要意义。
滚动轴承的动态特性研究经历了不断发展的过程。Jones[6]首先提出了滚道控制理论,建立了滚动轴承拟静力学分析模型,但该模型没有考虑弹流润滑的作用和保持架对轴承力矩的影响。Gupta求出了轴承运动和力的瞬态解,并且编制了大型应用程序ADORE[7]。Svenska Kullager-Fabriken公司开发的大型计算机分析软件“SHARBERTH”,采用拟动力学对滚子和保持架受力问题进行了分析和讨论。但该软件分析时考虑的因素比较多,程序过于庞大,求解时间较长,在工程应用中有一定的局限性。Aramaki[8]开发了滚动轴承动力学分析软件BRAIN,是目前能分析轴承类型最多的软件,但对润滑和摩擦阻力的研究仍有待完善。Stacke等[9]开发了BEAST三维分析软件,但对于部分膜润滑和挤压阻尼的计算还有待完善。
虽然动力学模型分析方法考虑的因素比较全面,但由于高速下滚动轴承各元件间动态特性非常复杂,考虑的因素较多,必然带来数学上求解的困难,因此滚动轴承动力学理论迄今为止仍不完善[10]。鉴于此,采用拟静力学分析的方法,对中介轴承动态特性进行研究。
1 基本假设
因中介轴承工作时内、外圈同时同向旋转,其受力和运动情况比外圈固定或内圈固定的轴承相对复杂,故求解中介轴承载荷分布时假设:
(1)滚子与内、外滚道之间均形成弹流润滑油膜,不存在乏油问题。
(2)滚子与滚道的接触中,只有滚子发生变形,忽略内、外滚道的变形。
(3)滚子与内、外圈的接触载荷对称于径向载荷作用线均匀分布。
2 模型建立
建立中介轴承在同向旋转时的拟静力学模型,分析轴承内部载荷的分布特征和运动特性。
2.1 滚子运动分析
简化的中介轴承滚子运动情况如图1所示。图中,Di为内滚道直径;De为外滚道直径;Dr为滚子直径;ωi为内圈角速度;ωe为外圈角速度;ωc为保持架角速度;ωrj为第j个滚子的角速度;ωruj为非承载区第j个滚子的角速度(未示出)。
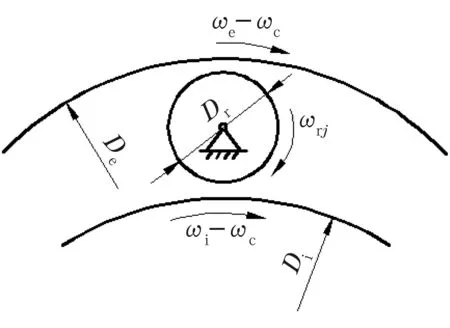
图1 中介轴承运动分析
滚子与内、外滚道之间的平均速度为
(1)
(2)

非承载区滚子与外圈滚道接触表面平均速度为
(3)
滚子与内、外滚道之间的相对滑动速度为
(4)
(5)
2.2 滚子受力分析
图2给出了滚子在承载区和非承载区的受力情况。承载区滚子受力如图2a所示,力和力矩的平衡方程组为
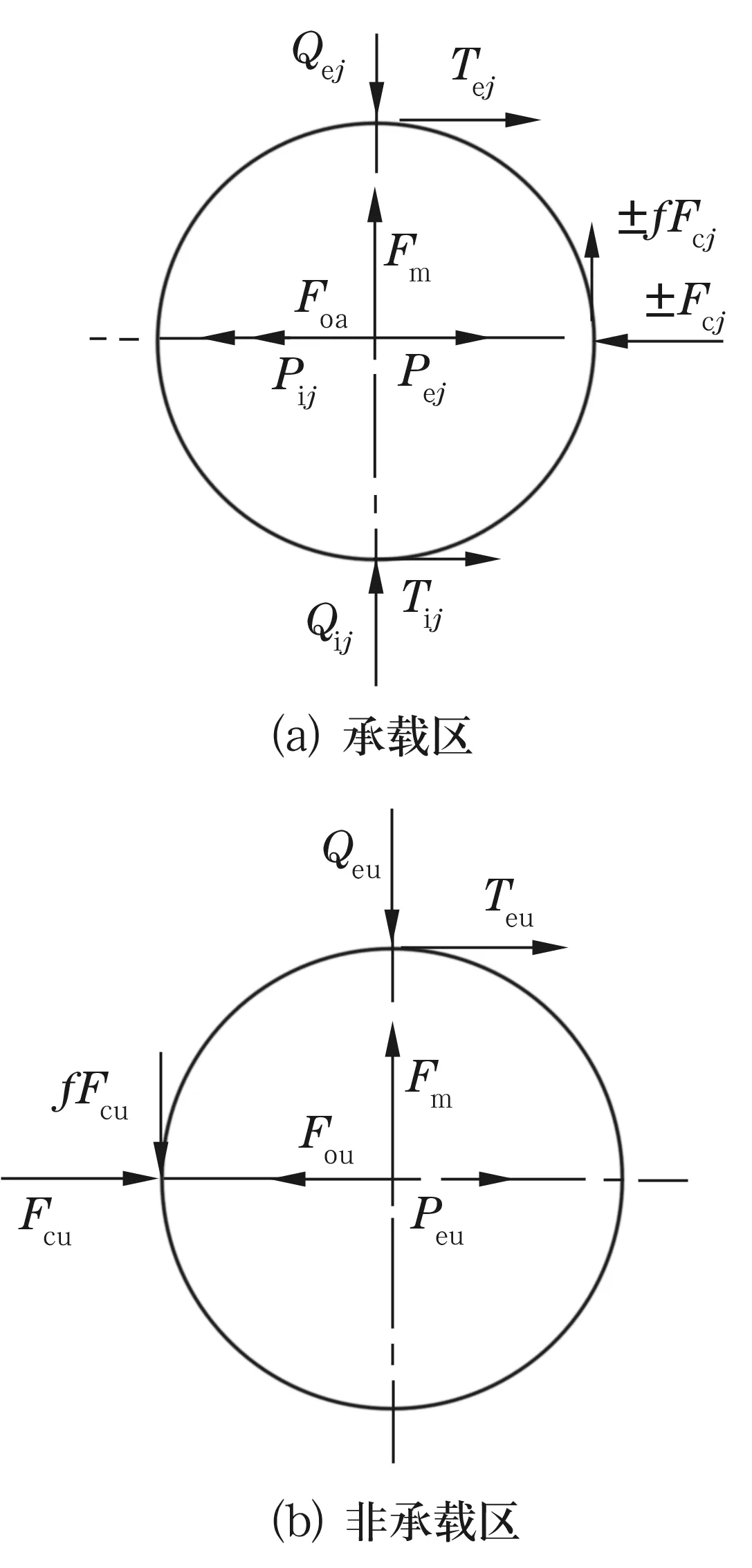
图2 滚子受力分析
(6)
式中:Qij,Qej分别为各个滚子与内、外圈滚道之间的接触载荷;Pij,Pej,Peu为作用于滚子的切向动压力;Tij,Tej,Teu为作用于滚子上的切向摩擦力;Fm为单个滚子的离心力;Foa,Fou为滚子受油气混合物的绕流阻力;Fcj,Fcu为承载区和非承载区滚子与保持架之间的作用力;f为摩擦因数。承载区内当保持架推动滚子运动时取正号,反之取负号。
将(6)简化合并得
(f-1)Tej+f(Pej-Pij)+(f+1)Tij-fFoa=0,j=0,1,2,…,N,
(7)
轴承正常工作时,保持架以匀角速度ωc平稳运转,因此保持架处于平衡状态, 其力矩平衡方程为
(8)
式中:Fc0为第0滚子与保持之间的作用力,z为总滚子数,2N+1为承载区内滚子数。
非承载区滚子受力分布如图2b所示,其力平衡方程为
Fou-Fcu-Peu-Teu=0。
(9)
(6)~(9)式中,各参数意义及求解方程如下。
2.2.1 滚子接触载荷Qij和Qej
中介轴承的动态载荷分布如图3所示,根据平衡条件可得

图3 中介轴承动态载荷分布
(10)
式中:Qi0为滚子与内圈之间的接触载荷。
内圈相对于外圈的位移量为
(11)
式中:Δ0为径向载荷作用下轴承内、外圈的相对位移;δj为第j个滚子与内、外套圈之间的接触变形;ur为轴承的径向游隙。
其中,第j个滚子总弹性变形量为
δj=δij+δej。
(12)
由文献[11]可得
(13)
其中,Kn为载荷变形系数,可参考文献[12]计算。
由(11)~(13)式可得承载区的变形协调方程
1.13(hij+hej)]=0,j=1,2,…,N。
(14)
联立(10)和(14)式,可求解N+1个未知数Qi0,Qi1,…,QiN。承载区滚子数为M=2N+1,考虑对称分布,为简化计算,故只求解N+1个未知数。
2.2.2 切向动压力Pij,Pej和Peu
轴承工作时,内、外圈之间的润滑油受到挤压对滚子产生切向压力[11],承载区切向动压力为
(15)
(16)
非承载区切向动压力为
(17)
其中,
(18)
(19)
(20)
2.2.3 切向摩擦力Tij,Tej和Teu
由文献[11]可知,内、外圈滚道通过油膜作用于滚子的切向摩擦力为
(21)
(22)
非承载区作用于滚子的切向摩擦力
(23)
其中,
(24)
(25)
(26)
无量纲积分
(27)
(28)
其中,
(29)
(30)
G=αE0;
(31)

2.2.4 单个滚子离心力Fm
由文献[13]可知,单个滚子离心力计算式为
(32)
式中:mb为滚子质量。
2.2.5 油气混合物对滚子的绕流阻力Foa和Fou
由文献[13]可知,滚子受油气混合物绕流阻力的计算式为
(33)
式中:Cd为绕流阻力系数;ρ为油气混合物的密度。
2.2.6 滚子与保持架之间的作用力Fcj和Fcu
承载区和非承载区滚子与保持架之间的作用力,由(7)式和(8)式组成方程组,采用Newton-Raphson法进行求解,具体过程略。
3 中介轴承动态特性分析
以某型号中介轴承为算例,其主要参数见表1。
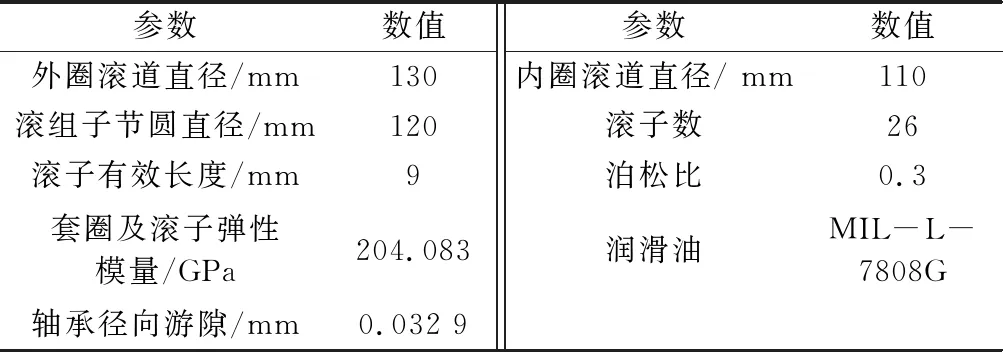
表1 中介轴承主要参数
图4为当内圈转速为5 000 r/min,外圈转速为10 000 r/min时,内圈与滚子之间的接触载荷随径向力变化图。可以看出随着径向力的增加,内圈与滚子之间的接触载荷随之增加。并且在1 000 N增至2 000 N时,承载滚子数增加。
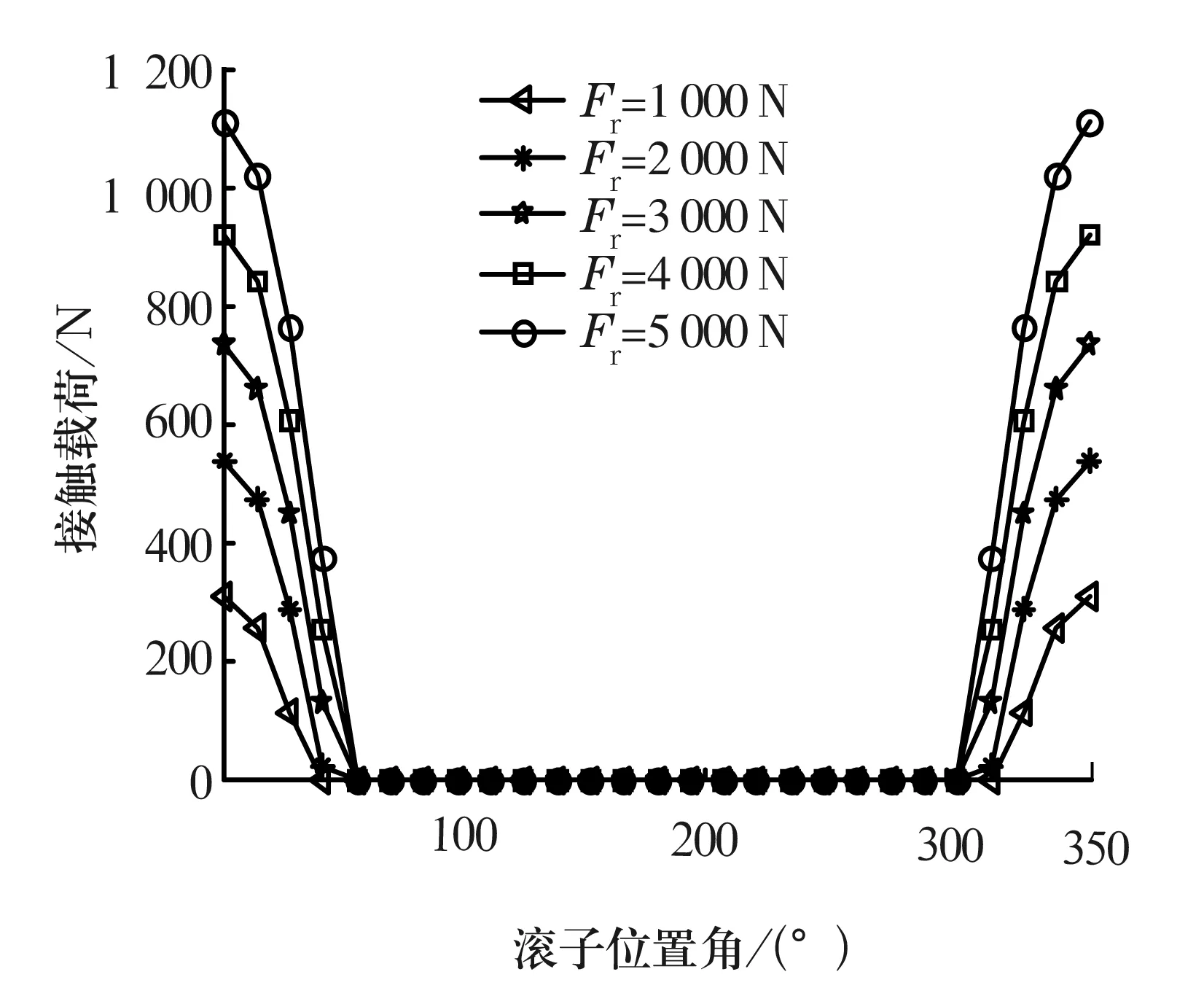
图4 内圈与滚子之间的接触载荷分布
图5所示为低压转子转速为5 000 r/min,高压转子转速为10 000 r/min时,中介轴承滚子自转角速度与径向力的变化情况。其中,0号滚子为受力最大的滚子,1,2,3号滚子位于0号滚子一侧,与0号滚子的距离等量递增。从图中可以看出,随着径向力的增加,承载区内各滚子的自转角速度随之减小,且滚子越偏离径向力作用线,自转角速度越大。 随着径向力的增加,受载区滚子与内圈间的法向接触载荷随之增大。滚子与外圈间的法向接触载荷也随之增大。但是由于离心力的作用,滚子与内圈接触载荷增加量小于滚子与外圈之间接触载荷的增加量,这使得内圈对滚子的牵引力增加量小于外圈对滚子的牵引力的增加量,从而使内外圈滚道作用在滚子上,使滚子自转的摩擦力矩减小,造成滚子自转角速度随之减小。在同一径向力的作用下,越接近径向力作用线的滚子,内、外圈滚道作用在其上的摩擦力矩越小,滚子自转角速度越小。在1 700~2 000 N时,因承载滚子数增加,内圈对滚子接触力和牵引力的减小量小于外圈对滚子接触力和牵引力的减小量,使得内、外圈作用在滚子上的摩擦力矩增加,致使滚子自转角速度随之增加。
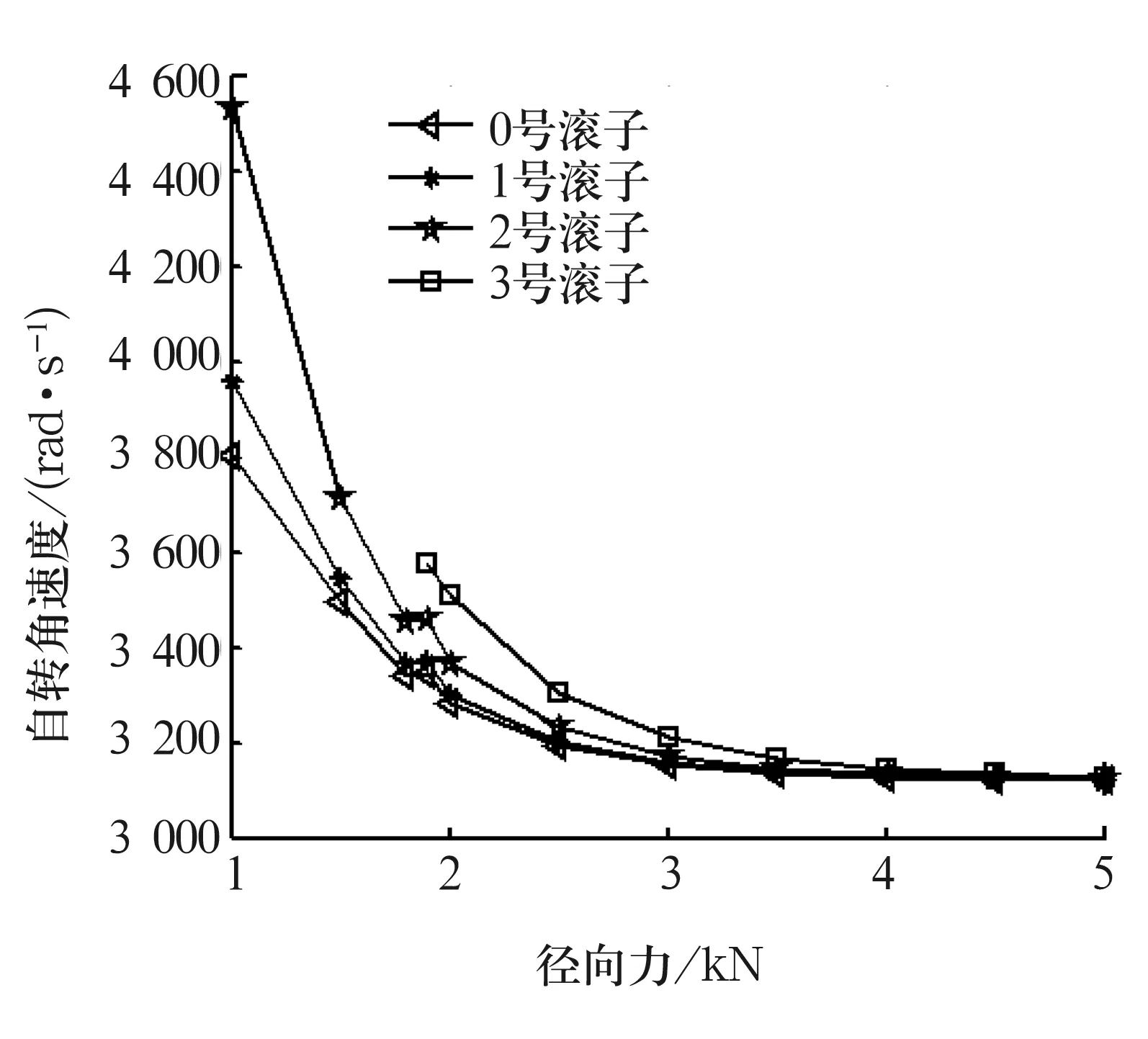
图5 滚子自转角速度随径向力的变化情况
图6和图7所示为径向载荷为2 000 N、内圈转速为5 000 r/min、外圈转速为13 000 r/min时,中介轴承滚子自转角速度分别随内、外圈转速变化情况。从图中可以看出:当中介轴承外圈转速增加时,各滚子自转角速度随之增加,而当内圈转速增加时,各滚子的自转角速度随之减小。这是因为当内、外圈转速增加时,其作用于滚子的牵引力减小,当外圈和滚子间牵引力减小时,内、外圈作用在滚子上的摩擦力矩增加,使得滚子自转速度增加;内圈和滚子间牵引力减小时,内、外圈作用在滚子上的摩擦力矩减小,致使滚子自转速度减小。
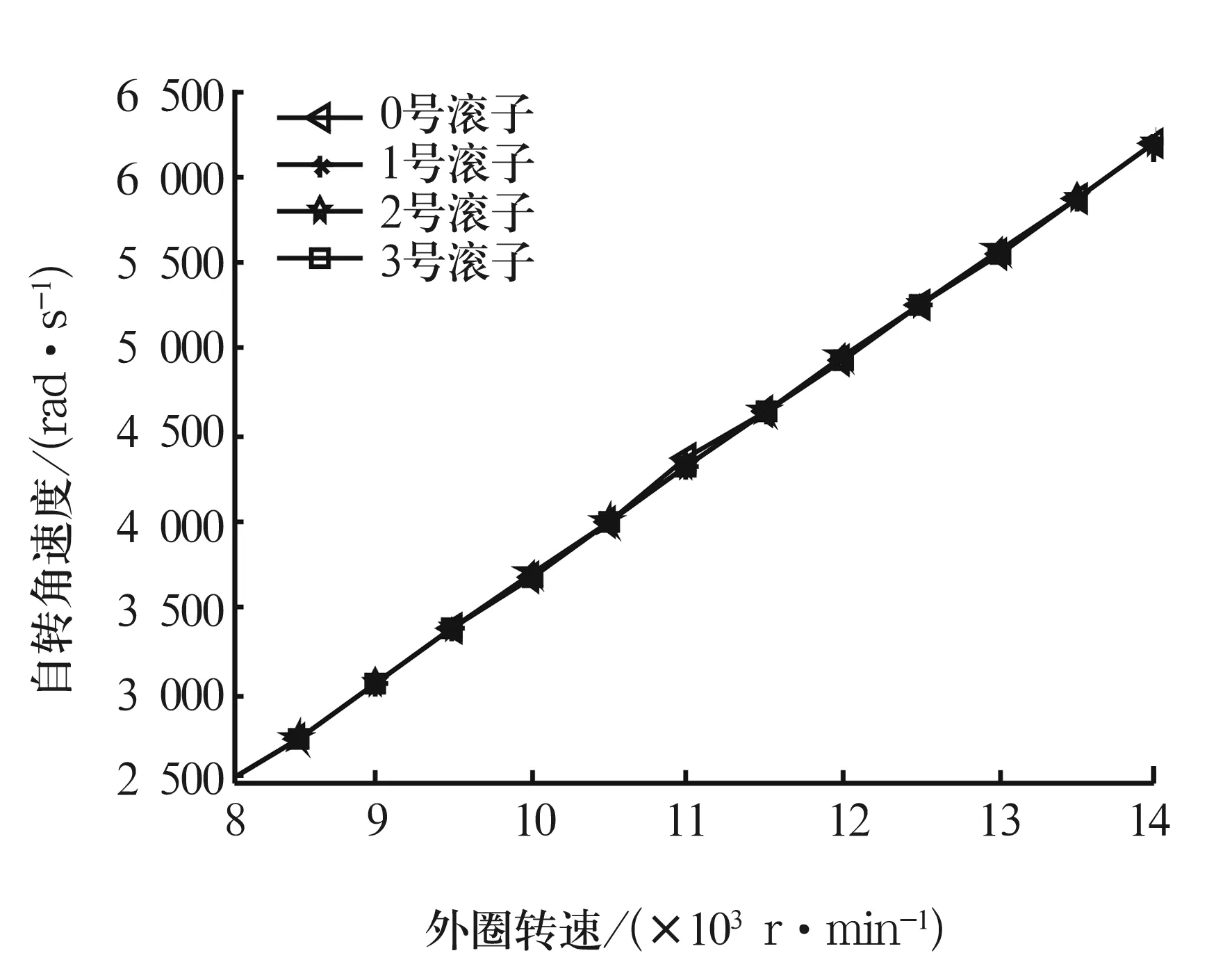
图6 滚子自转角速度随外圈转速的变化情况

图7 滚子自转角速度随内圈转速的变化情况
表2为内圈转速为5 000 r/min,外圈转速为10 000 r/min,套圈与滚子间油膜厚度与载荷的关系。从表2中可以看出,在承载区内滚子不变时,随着径向力的增加,油膜厚度减小,并且内圈滚道与滚子之间的油膜厚度小于外圈滚道与滚子之间的油膜厚度。

表2 轴承油膜厚度与载荷的关系
通过双转子试验机可以测得不同径向载荷下中介轴承保持架的转速。算例中的计算结果与试验结果比较,最大误差为4.28%,可见文中建立的中介轴承动态特性分析模型是正确的。
4 结论
(1)建立的中介轴承动态特性分析模型误差较小,可为中介轴承的设计提供理论指导。
(2)对于内、外圈同向旋转的中介轴承,随着径向力的增加,轴承承载区内各滚子的自转角速度随之减小。中介轴承承载区内各滚子越偏离径向力作用线,滚子自转角速度越大。
(3)对于内、外圈同向旋转的中介轴承,外圈转速增加时,各滚子自转角速度随之增加,而当内圈转速增加时,各滚子的自转角速度随之减小。
(4)径向载荷的大小对弹流润滑油膜的形成影响较大,适当地减小径向载荷有利于形成完全弹流润滑油膜,保证高速滚子轴承工作时能够达到良好的润滑状态。
