同序流水作业问题的建模及求解算法

赵金霞，沈 灏

(1.杭州电子科技大学电子信息学院，浙江杭州310018;2.杭州电子科技大学理学院，浙江 杭州310018)

0 引言

在调度问题中，Johnson算法成功地解决了 Flow Shop问题中的 n/m/F/Fmax(m=2)问题，而n/m/F/Fmax(m＞2)就是一个NP难题［1］，对此，有CDS以及用斜度指标排列作业的Palmer等启发式算法［2，3］。除了启发式算法，许多人也研究了用模拟退火算法和遗传算法等搜索技术来求解流水线调度问题，并取得了一定成果［4，5］。最新的求解方法有改进量子遗传算法和基于分布估计算法［6，7］。对于n项任务，两道工序，每道工序由若干台平行机组成，目标为makespan最小化的调度问题，要将n!次排列全部收索完毕才能得到最优解，随着n的增加，复杂度剧增。本文提出的Johnson序结合自然序的快速算法，既能提高求解效率，又能在尽量满足先到先服务规则的前提下达到客户要求。

1 问题描述

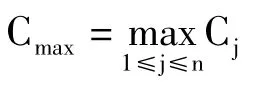
有一属于典型的同序流水作业调度问题的具体实例:某工厂要尽快赶出140项任务，其中工序1加工车间和工序2加工车间关于每项任务所需要的时间如表1所示，其中只列出6项，其余各项均省略。工序1加工车间共有12台平行机，工序2加工车间共有3台平行机，各车间按j1，j2，…，j140的自然顺序工作时，计算每个jk的开工时间和完工时间;若工厂希望整批任务能够尽早完工，以提高生产效率，又要尽量保证客户满意度，应如何安排任务的先后加工顺序，才能使完成所有任务的总工期最短。

表1 140项任务两道工序时间表

2 流水作业模型的建立及求解

2.1 模型假设

(1)每个任务的每道工序只在一台设备上完成，不能同时在几台不同的设备上加工，且加工过程中不能中断。

(2)每道工序完成后即可排到下一道工序队列里加工，不考虑两道工序中间的搬运等时间，也不考虑机器的调整时间。

(3)任务数、设备数和加工时间已知，加工时间与加工顺序无关。

(4)每台设备只能同时加工一项任务，每项任务前一道工序完成后才能进行下一道工序。

2.2 自然顺序下调度模型

由于要按照产品编号顺序进行加工，本文根据各项任务工序1的完成顺序得到工序2的加工顺序，同时考虑到工序2的平行机可能有空闲问题，编程计算得到各工序开始时间与结束时间，最终这140项任务在自然顺序下的总完工时间为236。

自然顺序下的算法思想如下:

(1)按照自然顺序，每一项任务都是先加工工序1再加工工序2，一台工序1平行机加工完，就对下一项任务进行加工;把完成工序1的任务依次放到一个队列里，如果工序2的平行机有空闲，就把队列里存着的任务拿出来加工;

(2)每台工序1平行机或工序2平行机上的后一项任务开工时间=前一项任务完工时间，即T后－项－项=T前－项－项;

(3)每项任务的工序1完工时间=此项任务工序1开工时间+此项任务所需工序1加工时间，即T工序1完工=T工序1开始+T工序1;

(4)每项任务的工序2完工时间=此项任务工序2开工时间+此项任务所需工序2加工时间，即T工序2完工=T工序2开始+T工序2;

(5)自然顺序下每一项任务的工序2开工时间=此项任务工序1完工时间+等待时间，即T工序2开始=T工序1完工+T等待，若工序2平行机有空闲，则等待时间为0。

2.3 Johnson序结合自然序的混合调度算法

2.3.1 算法设计

根据实际问题确定一个常数T，在自然顺序中截取一段总加工时长不超过T但尽量接近T的几个连续任务成为一个小组，组内工件应用Johnson序，但是组间工件采用先到先服务原则的自然序。T可根据不同厂商的实际情况选取，比如取平行机总数，或者工序1设备总数等。由于Johnson算法得到的是总加工时长最短序，可知混合算法在组内加工时长最短，所以总加工时长必然小于或等于纯自然序下的总加工时长。

设符号jk为任务k，k=1，2，…，n;P1k为第k个任务的第一道工序加工时间;P2k为第k个任务的第二道工序加工时间;Mi为第i台机器，i=1，2，…，m。

(1)工件集分成两个不交子集J1和J2，其中J1={jk|P1k＜P2k}，J2={jk|P1k＞P2k}，满足P1k=P2k的工件可以分在两个子集中的任何一个。

(2)先将J1中的工件按P1k的非降序排序，再将J2中工件按P2k的非增序排序。

设机器M1上的第一个工件的开工时间为t=0，工件的加工顺序为j1，j2，…，jn，则第k个工件jk在机器Mi上的完工时间可以用以下递推公式计算［1］:

2.3.2 Johnson算法结合自然序求解

(1)用MATLAB编程将140项任务分成两个子集合:工序1加工时间小于或等于工序2加工时间的任务集合J1={j1k}，工序1加工时间大于工序2加工时间的任务集合J2={j2k}，并将J1整理成关于工序1 加工时间的非降序，k 依次为:43，57，4，...，102，32，27，共 36 项;J2整理成关于工序 2 加工时间的非增序，k 依次为:41，111，133，...，68，105，116，共 104 项。

(2)先加工J1中的任务，后加工J2中的任务，即得总工期最短的加工顺序Jk。

(3)把Jk带入到自然顺序的程序中去，得到每项任务由12台工序1平行机和3台工序2平行机加工时的各自开始时间与结束时间，最终这140项任务在Johnson算法结合自然序求解下的总完工时间为229，比单纯的自然顺序下的总完工时间短。

2.4 实例验证

在实际生产中，任务集的给出具有很大的随机性，而且考虑到顾客的满意度问题，厂家要尽量保证顾客按先到先服务的自然顺序完成任务，所以用计算机随机模拟出3种任务集(假设有10项任务，4台工序1平行机，1台工序2平行机)，即工序1时间非递增工序2时间非递减序列、工序1时间非递减工序2时间非递增序列、工序1时间和工序2时间均服从泊松分布的3种序列，分别如表2－4所示，以此举例验证Johnson序结合自然序混合型算法在许多实际问题中具有一定的应用价值。

表2 工序1时间非递增工序2时间非递减任务集 (h)

表3 工序1时间非递减工序2时间非递增任务集 (h)

表4 工序1时间和工序2时间均服从泊松分布任务集 (h)

表3的情况下，自然顺序和混合型算法下的完工时间相同，因为J1恰好是关于工序1时间的非降序，J2恰好是关于工序2时间的非增序，和此情况下的自然顺序一样，故结果相同。

由于顾客流一般服从泊松分布，所以模拟得工序1时间和工序2时间均服从泊松分布的任务集。

从以上3个例子可以看出Johnson序结合自然序的混合型算法优于纯自然序。

3 结束语

Johnson算法的特点是求得总加工时长最短序，但实际生产中，这样可能会造成先到任务延期太长而不能被客户接受的情况，而混合算法既体现了Johnson算法总加工时长最短的优点，又可以避免此种情况的发生，可见Johnson序结合自然序的混合型算法具有很强的实践可行性。

［1］ 陈光亭，裘哲勇.数学建模［M］.北京:高等教育出版社，2010:60－61.

［2］ Dudek R A，Panwalker S S，Smith M L.The lessons of Flowshop scheduling research［J］.Operations Research，1992，40(1):42－46.

［3］ Palmer D S.Sequencing jobs through a multi-stage process in the minimum total time-A quick method of obtaining a near optimum［J］.Operations Research Quart-erly，1965，16(1):101 － 107.

［4］ 田彭，杨自厚.同顺序排序问题的模拟退火求解［J］.信息与控制，1994，23(3):133－139.

［5］ 熊红云，何钺.模糊Flow－shop问题及其遗传优化［J］.信息与控制，1999，28(1):8－13.

［6］ 王兴林，李茂军.基于改进量子遗传算法的Flow－Shop调度求解［J］.计算技术与自动化，2010，29(3):82－85.

［7］ 叶宝林，高慧敏，王筱萍，等.基于分布估计算法的二阶段置换流水车间调度算法［J］.计算机应用研究，2011，28(10):3 702－3 706.