连续型随机变量函数概率密度的教学方法探讨

孙春香

（淮南师范学院 数学与计算科学系，安徽 淮南 232001）

连续型随机变量函数概率密度的教学方法探讨

孙春香

（淮南师范学院 数学与计算科学系，安徽 淮南 232001）

本文从单个随机变量的函数和两个随机变量的函数的概率分布两种情形分别探讨随机变量函数的概率密度的求解方法.

随机变量；密度函数；随机变量函数；卷积公式

1 引言

随机变量函数的分布问题是概率论与数理统计中的一项重要的问题，它在随机变量研究中占有非常重要的意义，是整个随机变量研究的核心内容，关于许多随机变量的研究都是通过研究随机变量函数的分布问题得以发展.因此，在这部分的学习中，掌握其方法和解题技巧至关重要.以下就是作者凭借多年从事概率统计课程教学的经验总结了几点看法.

2 单个随机变量函数的密度函数的求法

对于这种类型的问题，主要通过某个随机变量的密度函数f(x)来找出Y=g(X)的密度函数f Y(y)，主要介绍一下两种方法.

2.1 “分布函数法”——求解问题的万能公式

“分布函数法”是解决随机变量函数的密度函数的一般方法，可以赋予其“万能公式”的称号.其原因是不管y=g(x)的形式多么复杂，均可采用此方法.具体步骤如下：

（1）先由X的值域ΩX，确定出Y=g(x)的值域ΩY；

注1：所谓值域通常指的是随机变量密度函数表达式的非零区间.

（2）对于任意的y∈ΩY，Y的分布函数

(其中G y={x|g(x)≤y})；

（3）写出FY(y)在(-∞,+∞)上的表达式；

（4）求导得到f(y)=Fy'(y).

例1已知X-N(0,1)，试求Y=2 X2+1的密度函数f(y).

解 由已知得X的密度函数为

易知随机变量X的非零区间为ΩX=(-∞,+∞)，

从而由Y=2 X2+1≥1得到ΩY=(1,+∞)，

所以当y≤1时Fy(y)=0

当y>1时，F Y(y)=P(Y≤y)=P(2 X2+1≤y)

所以当y>1时，两边对y求导数得到

注2：在非零区间上找分布函数时，不一定求出其具体的表达式，因为在以上问题中，我们的目的是求出Y的密度函数，分布函数只是一个中间过渡，可运用X的分布函数给出Y的分布函数的形式表达式，利用复合函数求导可以直接给出其密度函数，这样在很多类似问题中可使问题简单化.

2.2 特殊求解——公式法

当g(x)为严格单调时，可运用以下定理直接得出结论.

定理1设X是连续随机变量，其密度函数为fX(x).Y=g (X)是另一个随机变量.若y=g(x)严格单调，其反函数h(y)有连续导函数，则Y=g(x)的密度函数为

其中ΩY为随机变量Y的非零区间.

证明 见参考文献[1].

例2设X-N(μ,σ2)，求Y=3 X+2的概率密度函数.

注3：通过例题可以看出运用定理1解决问题很是简便，但是要注意其适用的条件，这点在学习中容易被忽视.例如读者可以考虑当X-U(0,π)及时Y=s i n X的密度函数的求解方法的异同.

由定理1，对于正态分布，还有如下结论

定理2设随机变量X服从正态分布N(μ,σ2)，则当a≠0时，有Y=a X+b-N(a μ+b,a2σ2).

证明 当a>0时，Y=a X+b是严格增函数，仍在(-∞, +∞)上取值，其反函数为X=(Y-b)/a，由定理可得

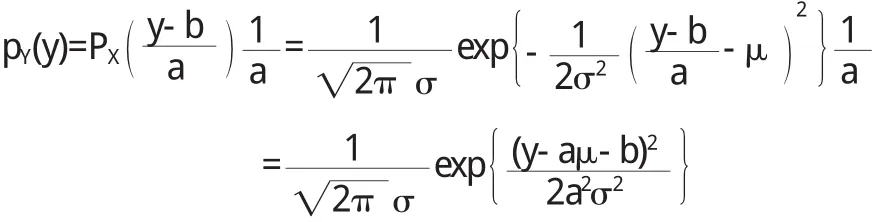
这就是正态分布N(μ+b，a2σ2)的密度函数.

当a<0时，Y=a X+b是严格减函数，仍在(-∞,+∞)上取值，其反函数为X=(Y-b)/a，由上定理可得

这是正态分布N(a μ+b，a2σ2)的密度函数，结论得证.

这个定理表明，正态变量的线性变换仍为正态变量，其数学期望和方差可直接从线性变换求得.若取a=1/σ，b=-μ/σ，则Y=a X+b-N(0,1).这在概率论与数理统计中意义重大.

例3设随机变量X-(10,22)，试求Y=3 X+5的分布.

解 由定理2知Y仍是正态变量，其数学期望和方差分别为

所以Y=3 X+5的分布为N(3 5,62).

3 两个连续随机变量的函数的密度函数的求法

这部分涉及到的问题和第二节的问题极其类似，只是把一维的问题推广到二维当中去，因此，解决的方法也极其类似.

3.1 “分布函数法”——求解问题的万能公式

若已知(X,Y)的联合概率密度为f(x,y)，欲求Z=g(X,Y)的概率密度fZ(z)，解决此类问题仍然采用以下4步：

（1）先由(X,Y)的值域确定出Z=g(X,Y)的值域ΩZ；

（2）对于任意的z∈ΩZ，求出Z=g(X,Y)的分布函数；

（3）FZ(z)写出 在整个坐标平面上的表达式；

（4）求导，即可得Z=g(X,Y)的概率密度

通常，我们也称这种方法为“分布函数法”，它适用于任何一种函数形式下Z=g(X,Y)的密度函数的求解，是前面“分布函数法”的推广.

当z<0时，FZ(z)=0，

当z>0时，FZ(z)=P(Z≤z)

所以FZ(z)，两边对z求导数得

3.2 特殊求解——公式法

“分布函数法”虽然能解决所有的问题，但因为涉及到二重积分的计算问题，操作起来相当复杂.因此，对于常见的和、差的分布，商的分布，乘积的分布给出下面的求解公式.

定理3已知(X,Y)的联合概率密度为f(x,y)，则

（1）Z=X++Y的密度函数

（2）Z=X-Y的密度函数

（3）Z=X/Y的密度函数

（4）Z=X Y的密度函数

d x其中（1）和（2）分别称为和、差的卷积公式.

解 由卷积公式

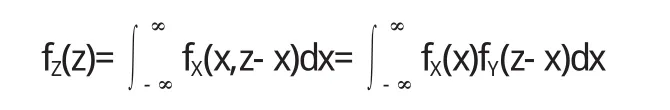
为确定积分限，先找出使被积函数不为0的区域

注4：通过上面例5可以看出，运用公式过程相对简单，但在确定分段函数的非零区间时，需要解出一个含参数的不等式组，值得读者特别关注，这也是公式法的不足之处.

4 小结

本文所得出的结论对随机变量函数的学习具有一定的指导意义，虽然现有对随机变量函数的研究已经比较成熟，但要想对随机变量函数有更深一步的认识，还有待于进一步的发展.

〔1〕盛骤，等.概率论与数理统计[M].高等教育出版社，2008.〔2〕茆诗松，程依明，濮晓龙.概率论与数理统计教程[M].高等教育出版社，2004.

〔3〕陈仲堂.赵德平.概率论与数理统计[M].高等教育出版社，2012.

〔4〕张菊芳，陈宁，章晓，等.概率论与数理统计[M].化学工业出版，2011.

〔5〕唐兴芸，罗明燕.二维连续型随机变量函数的概率密度[J].黔南民族师范学院学报，2012(2):112-115.

〔6〕崔静.关于一维与二维连续型随机变量函数的分布探讨[J].西安文理学院学报，2007(10):32-36.

G642

A

1673-260 X（2013）10-0227-0 2

安徽省高等学校优秀人才基金研究项目资助(2011SQRL136)；淮南师范学院教学研究项目资助(2012hssjk10)