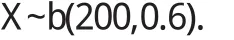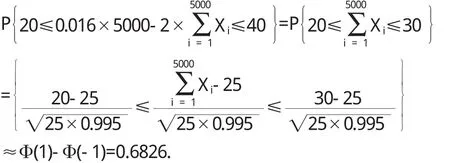论中心极限定理及应用

王伟珠

（辽宁对外经贸学院 基础课教研部，辽宁 大连 116052）

论中心极限定理及应用

王伟珠

（辽宁对外经贸学院 基础课教研部，辽宁 大连 116052）

中心极限定理是DeMoivre在18世纪首先提出的，定理在很一般的条件下证明了无论随机变量Xi(i=1,2…)服从什么分布，n个随机变量的和当n→∞时的极限分布是正态分布.本文仅介绍其中两个最基本的结论并举例应用.

中心极限定理；结论；应用

在实际问题中,许多随机现象是由大量相互独立的随机因素综合影响所形成,其中每一个因素在总的影响中所起的作用是微小的.这类随机变量一般都服从或近似服从正态分布.以一门大炮的射程为例,影响大炮的射程的随机因素包括:大炮炮身结构的制造导致的误差,炮弹及炮弹内炸药在质量上的误差,瞄准时的误差,受风速、风向的干扰而造成的误差等.其中每一种误差造成的影响在总的影响中所起的作用是微小的,并且可以看成是相互独立的,人们关心的是这众多误差因素对大炮射程所造成的总影响.因此需要讨论大量独立随机变量和的问题.

中心极限定理回答了大量独立随机变量和的近似分布问题,其结论表明:当一个量受许多随机因素(主导因素除外)的共同影响而随机取值,则它的分布就近似服从正态分布.而正态分布有许多完美的理论，从而可以获得即实用又简单的统计分析结果.本文仅介绍其中两个最基本的结论，并通过举例加以应用.

1 Lindeberg—Levy定理

定理1(Lindeberg—Levy定理)设X1,X2,…,Xn,…是独立同分布的随机变量序列,且

则对任意实数x，有

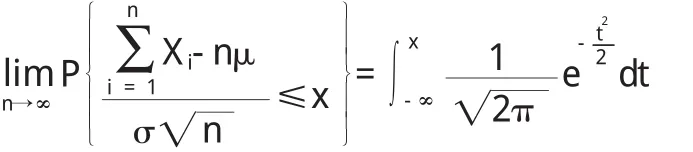
注1:该定理表明:当n充分大时,n个具有期望和方差的独立同分布的随机变量之和近似服从正态分布.虽然在一般情况下,我们很难求出X1+X2+…+Xn的分布的确切形式,但当n很大时,可求出其近似分布.由定理结论有

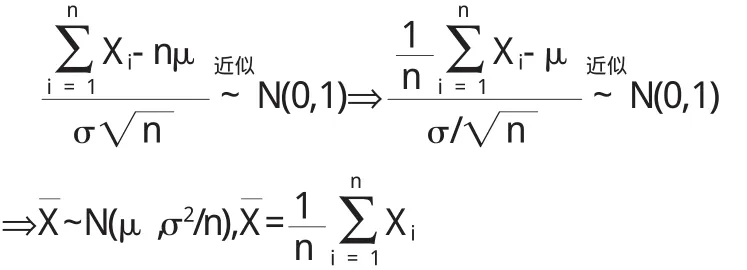
故定理又可表述为:均值为μ,方差为σ2>0的独立同分布的随机变量X1，X2，…，Xn的算术平均值,当、充分大时近似地服从均值为μ,方差为σ2/2的正态分布.这一结果是数理统计中大样本统计推断的理论基础.

2 棣莫佛—拉普拉斯定理

定理2（棣莫弗—拉普拉斯定理） 设随机变量Yn服从参数n,p(0

注2:易见，棣莫弗—拉普拉斯中心极限定理就是Lindeberg—Levy中心极限定理的一个特殊情况.

注3:中心极限定理存在的条件整理为如下几个关键词：独立、同分布、数学期望与方差存在；当随机变量序列满足中心极限定理时，难点是求解随机变量和函数的数学期望和方差，进而进行标准化就可以得到近似服从标准正态分布.

3 应用举例

例1 一盒同型号螺丝钉共有100个,已知该型号的螺丝钉的重量是一个随机变量,期望值是100g,标准差是10g,求一盒螺丝钉的重量超过10.2 kg的概率.

解 设Xi为第i个螺丝钉的重量,i=1,2,…,100.且它们之间独立同分布,于是一盒螺丝钉的重量为X=且由，知

E(X)=100×E(Xi)=10000，由中心极限定理有

例2 计算机在进行数学计算时,遵从四舍五入原则.为简单计,现在对小数点后面第一位进行舍入运算,则误差X可以认为服从[-0.5,0.5]上的均匀分布.若在一项计算中进行了100次数字计算,求平均误差落在区间/20]上的概率.

解 n=100,用Xi表示第i次运算中产生的误差.X1,X2,…,X100相互独立,都服从[-0.5,0.5]上的均匀分布,且E(Xi)=0,D (Xi)=1/1 2,i=1,2,…,100,从而,近似地有

例3 某车间有200台车床,在生产期间由于需要检修、调换刀具、变换位置及调换工作等常需停车.设开工率为0.6,并设每台车床的工作是独立的,且在开工时需电力1千瓦.问应供应多少瓦电力就能以99.9%的概率保证该车间不会因供电不足而影响生产?

解 对每台车床的观察作为一次试验,每次试验观察一台车床在某时刻是否工作,工作的概率为0.6,共进行200次试验.用X表示在某时刻工作着的车床数,依题意,有

现在的问题是:求满足P{X≤N}≥0.999的最小的N.

例4 某市保险公司开办一年人身保险业务,被保险人每年需交付保险费160元,若一年内发生重大人身事故,其本人或家属可获2万元赔金.已知该市人员一年内发生重大人身事故的概率为0.005,现有5000人参加此项保险,问保险公司一年内从此项业务所得到的总收益在20万到40万元之间的概率是多少?

于是Xi均服从参数为p=0.005的两点分布,且p{Xi=1}=0.005，np=是5000个被保险人中一年内发生重大人身事故的人数,保险公司一年内从此项业务所得到的总收益为0.016×5000-2×万元.于是

例5 对于一个学校而言,来参加家长会的家长人数是一个随机变量,设一个学生无家长,1名家长,2名家长来参加会议的概率分别为0.05,0.8,0.15.若学校共有400名学生,设各学生参加会议的家长数相互独立,且服从同一分布,求参加会议的家长数X超过450的概率.

解 以Xk(k=1,2,…,400)记第k个学生来参加会议的家长数,则Xk的分布律为

Xk 0 1 2 Pk 0.05 0.8 0.15

易知E(Xk)=1.1,D(Xk)=0.19,k=1,2,…,400,而X,由定理1,随机变量

例6 设有1000人独立行动,每个人能够按时进入掩蔽体的概率为0.9.以95%概率估计,在一次行动中,至少有多少人能够进入掩蔽体.

解 用Xi表示第i人能够按时进入掩蔽体,令Sn=X1+X2+…+X1000.设至少有m人能进入掩蔽体,则要求

m=900-15.65=884.35≈884人.

中心极限定理的应用很多，能解决更多的实际问题,有待于我们进一步的探讨.

〔1〕吴赣昌.概率论与数理统计（经管类·第三版）．中国人民大学出版社，2009.

〔2〕全国硕士研究生入学统一考试辅导用书编委会.数学考试参考书，高等教育出版社.

O211.9

A

1673-260 X（2013）10-0001-02