期权定价模型评估对赌协议相关价值的探讨
2013-07-07王少豪
■王少豪
对赌协议能够在买方和卖方之间架设协商的桥梁,从而促进交易的成功。特别是在目标公司未来预测前景高度不明朗的情况下,这样的协议条款能够解决交易双方由于预测的差异、信息的不对称等所造成的分歧。作者提供了一个对对赌协议期权价值进行价值评估且易于操作的评估模型以及案例演示,以便为投资并购中对赌协议的设计或PE、VC的企业估值提供有价值的参考意见。
一、概述
对赌协议的具体条款形式多样:不仅可以赌被投资企业的销售收入、净利润等财务绩效,还可以涉及非财务指标的赎回补偿、企业行为、股票发行和管理层去向等方面。但无非是现金、股权、管理以及控股等这些筹码。其中最简单的就是只支付现金,这种对赌协议条款也被称为盈利能力支付计划(earn-out)。
该协议条款模式实际上就是将传统的一次性付款方式转变成两次或多次付款的交易模式。而后面的款项则是按照未来一定时期内的业绩表现进行支付。通常是并购方根据被并购方将来的盈利能力,在未来再另外支付给被并购方现金。这里不涉及股权、经营权限等,仅涉及现金,所以相对比较简单。实际上这是买方在规避估值风险。即被收购公司如果未来收益达不到目标,则只值买方第一次首付的款项。如果未来收益能达到目标,则表明第一次的付款还不足以体现这个企业的价值,所以买方需要根据企业的经营业绩估算对应的价值增量,然后才把剩下的钱补偿给卖方。交易是否值得,决策交易是否继续进行,就取决于固定的原始付款再加上对赌协议选择权的价值。因此,对赌协议的价值评估成为核心。
二、对赌协议条款分析
在并购中采用这种对赌协议条款的主要原因是要解决买方与卖方对目标公司未来经济预期的差异。此外一个原因可能就是买卖双方的信息不对称。不对称源于这样一个事实:即卖方作为企业的内部人,应该是比买方更多地了解目标企业及其未来前景。即使买方对目标企业作了详尽的尽职调查也很难达到卖方自己所掌握的信息水平。
对于买方来说,投资并购始终存在着风险,即卖方总是展示企业经济前景的最佳状态。这里有两种可能:其一,卖方的展示是正确的判断,买方不可不信也不可能全信;其二,卖方的展示是错误的判断或有意误导而使买方误入歧途。因为根据评估原理,目标企业的价值,以及最后的交易价格均取决于企业期望的未来经济收益,所以买卖双方有可能由于在价格上不能达成一致而导致交易失败。在这种情况下,对赌协议条款也许能够有效地促成交易的完成。
由于随后的付款可能因目标企业的盈利而实现,所以买方可能愿意接受这样一个总的交易价格(固定的一次性付款价加上对赌协议的付款条款),这样的价格超出了原来买方可接受的一次性立即付款的最高价格。另一方面,卖方接受了一个较低的初始付款价格而得到一个随经济前景看好的选择性条款。如此一来,如果初始付款价格加上对赌协议条款的价值超过卖方心理的最低可接受价格的话,这个协议就有可能得以完成。
对赌协议条款的结构决定了风险在卖方和买方之间的分配。一般来说,从买方的角度来看,对赌协议能够降低双方的风险差异。首先,由于接受对赌协议条款,就说明卖方对对赌协议认定的经济前景的可靠性表示认同,这无疑降低了买方作为信息偏少方的风险。其次,由于对赌协议的付款是基于目标企业的经济前景,所以卖方继续承担着企业的部分风险。此外,如果卖方仍然对企业的经营产生影响的话,或者作为企业董事会成员,则对赌协议给卖方提供了一个激励的动力,来帮助企业达到预期的盈利目标从而使协议的付款能够实现。
对赌协议的吸引力随着对未来经济预测的不确定性的增加而增加。当不确定性增加时,也就增加了双方在交易价格上认识一致的难度。而这种不确定性增加的情况在当前金融危机和经济危机的大环境下是很普遍的现象。为了应对这种高度的不确定性,目前对赌协议被广泛采用。很多情况下,它是交易的先决条件。对赌协议促成了一个较低的初始付款金额,且这个金额也是卖方可以接受的,因为如果经济进程顺利,协议确定的随后的付款也就会随之而来。而从买方的观点来看,对赌协议使其付款总额分成两部分,一部分可以延迟支付,因此有利于保证其资金的充足流动性。
三、几种常见类型的协议条款设计
在对赌协议中,通常总的价款分成两个部分:第一部分是固定的一次性付款,一般是立即支付;而另一个可变的随后付款,是根据未来可实现的某些财务或经营指标来兑现,如销售收入、EBIT、现金流等。一般来说,与对赌协议条款挂钩的经营指标的实现应满足一定的要求,被认为是客观的、可测量的和准确的。
在经营指标被确定之后,协议条款的关键就是可变后续付款的方式。一般情况下,为了确定可变对赌的部分,买方和卖方会事先定义一个执行指标的最低门槛,即被投资企业在未来某个时间的经营业绩指标应达到某个规定的数字。如果超过这个数字,那么卖方就可以得到原先预期的后续第二笔付款。而后续的付款可以设计为三种形式:
1. 卖方直接参与目标企业盈利的分红(按一定比例),也就是说,后续的付款是从企业本身的盈利里面提取,企业在未来某个时间或时间段的盈利越多,那么卖方得到的后续付款也就越多。后续付款与企业未来盈利是一个线性的比例关系。图1展示了这一可能对赌协议条款的支出情况。由图可见,如果企业运行状况指标超过门槛K,则卖方按比例分享利益的状况。而且这个分红是上不封顶,我们称之为没有限制帽。
2. 对于图2的情况,则稍有不同。即随后的付款也是参与目标企业的盈利分红,但这个分红是有限度的。它是一个变量,即当经营指标超过水平U以后支付水平保持不变。即它是下有一个门槛,上有一个门顶,或者叫限制帽。超过门槛可以按盈利的比例获得分红作为补偿,而当盈利达到或超过限制帽的时候,卖方获得的补偿就不再是按比例分红,而是一笔固定的补偿款。
3. 对于图3,所示情况为:如果企业经营状况指标超过门槛K,对赌协议条款就兑现一个稳定的后期支付款。
对赌协议条款的设计应是相对灵活的,除上述三种基本方式之外还可以设计出更多的结构来。本文只是想就上述三种情况展示运用评估模型的方法。

图1

图2

图3
上述三种典型的对赌协议条款结构都具有期权的特征,即卖方只有在企业未来经营良好的情况下才能分享利润。为了确定一个合适的经营指标门槛值,以便与对赌协议条款挂钩,通常由卖方根据企业经营历史数据提出,或者是历年平均值,或者是预测的数据。同时,对赌协议的时间周期即有效期也要确定,一般来说协议的周期长度是三到五年。
四、选定价值评估模型
(一)协议条款的期权类型
为了评估对赌协议的价值,我们首先把协议条款与类似的股票金融期权相比较。从股票期权的组合来看,买权和卖权各自都可以买进和卖出,因此,就有了4种基本的期权头寸。其内在价值见图4。
上述分析的对赌协议条款模式和股票期权相类似。比如,第一种付款模式(图1)就类似于欧式多头买方期权的内在价值(其中的约定价格为K),即图4中的(a)图。而第二种付款模式(图2)的情况,不是一种单个的期权,而是多头买权和空头买权的结合,即图4中的(a)和(c)相结合,结合后如图5。最后,第三种付款模式(图3)就对应一个两值期权,即如果股票价格在到期日超过约定价格,则应允给出固定的支付,即如上面的图3所示。
依此类比,这三种对赌协议条款设计模式我们都可以应用期权定价理论来进行评估。第一和第二种条款可采用布莱克—舒尔斯期权定价模型。但是由于这个模型是建立在约束性假设前提基础上的,所以不可能是完全直接应用。这个模型的关键假设是期权所针对的股票有对数正态分布的特性,而且是在十分活跃的市场中进行交易的。关于分布的假设对于对赌协议中的运营财务指标可能相对符合(如EBIT等),而活跃市场的假设很难实现,因为这些指标都是没有交易的。我们可以通过应用一个所谓的“风险中性扩展框架”的评估方法,来避免这个问题,从而得到一个近似的结果。这在应用期权定价理论评估非贸易性资产的实物期权时是经常应用的方法,而这个应用结果在大部分的实际问题中也都是可以接受的。
第三种付款模式是一个典型的两值期权,可应用两值期权的计算公式。

图4 股票期权的内在价值

图5 多头买权与空头买权结合
(二)关于风险中性评估
风险中性定价是衍生证券分析中的一个重要工具,来源于B-S-M微分方程的一个关键性质,即:方程中不包含任何受投资者风险偏好影响的变量,所有的变量都独立于风险偏好。正因为风险偏好对期权定价没有影响,我们就可以使用任何一种风险偏好对其定价。可以假设所有的投资者都是风险中性的,这就是所谓的风险中性世界。在风险中性的世界里,所有证券的预期收益率皆为无风险利率,而任何现金流的现值都可以通过将其期望值用无风险利率折现来得到。如此大大地简化了期权定价的分析,但这样得出的结论却并不仅限于风险中性世界,而是对各种风险的状况都是有效的。
推导B-S模型有两种方法,一种是在微分方程基础上利用边界条件求解,可以得出解析的布莱克-舒尔斯期权定价模型。但是由于这种模型有着严格的边界条件,一般很难直接应用于非贸易资产的实物期权评估。另一种方法即是采用风险中性的评估方法。如考虑一个欧式看涨期权在风险中性世界中,到期时期权的期望值为:

这里 表示期权在风险中性世界中的期望值。由于是到期时的价值,所以评估现时期权价值c时应该用无风险利率来折现,即:

如果这里ST是T时刻的股票价格,根据B-S-M模型假设的随机过程,ST服从对数正态分布。并根据得到证明的关键结论:

可以得出上面欧式看涨期权在风险中性世界中,现时期权的价值为:
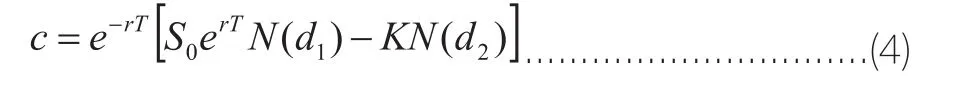
即:

其中

以上(5)式就是B-S-M期权定价模型对看涨期权的解析方程。但是对于非贸易性资产的实物期权问题,需要在原有的中性风险估值的框架上进行扩展。此时,我们设实物期权的变量为X,约定价格为K,则到期时期权的期望值为:

此处:

这里N(d1)是累积标准正态分布值,而σ则表示主变量X的离散程度(标准差)。此外, 是变量X在T时刻当中性风险的概率测度为某值时候的期望值。对于非贸易性资产,此时中性风险世界中的利率不再是一个常数,而是一个随机变量。所以,如果执行测度变量X在时刻T=0时的价值为X0,则对于时刻T且在风险中性的期望值为:

这里新引入几个变量,μ为变量X的期望增长率,λ为市场风险价格。在符合边界条件的传统风险中性世界中,假定所有风险市场价格都等于零,而对于实物期权来说,此时市场风险价格不再为零。因此,这个期望值是风险调节后的实际期望值。市场风险价格λ可以采用资本资产定价模型(CAPM)求出。根据CAPM模型,风险的市场价格λ由下列方程得出:

这里ρ是执行测度变量X变化百分比与股票市场组合价格指数收益之间的瞬态相关系数。参数σM表示市场组合指数收益率的波动率。而µM表示市场组合指数的预期收益率。为避免直接估算上述相关系数ρ和波动率σM,我们可以采用公司的风险系数β近似地得出风险中性的期望值。这种近似还是可信的,前提是企业运营的测量值如EBIT是以类似方式与市场组合的权益价值相关。在这种情况下,风险中性的期望值如下式所列:

从而

公式(11)就是我们针对上面对赌协议第一和第二种付款模式,所采用的布莱克—舒尔斯期权定价模型。而式中的d1和d2即和公式(6)一样。
(三)关于分成率
如果卖方在企业经营财务指标超过设定的门槛值时,可以参与分享利益成果,可以说卖方相当于持有一个欧式买方期权。预先设置的门槛相当于期权的约定价格K,而对赌协议中确定的付款时间可以看成是期权的到期日。但是协议一般是规定一定的补偿方案,即卖方在企业运营指标超过价值K的时候能够获得一定补偿。实际的对赌协议中会有许多不同的卖方补偿方案。比如说让卖方参与分享成果的50%。因此我们就需要采用一个乘数因子α来乘以上面求出的期权价值c。那么,真正对赌协议的价值EO就等于:

这个乘数因子α就是在出现正的溢差(XT-K)的时候,卖方参与分享利益的比例。
(四)有限制帽的情况
如果可变的补偿量有一个上限,即限制帽,则其价值评估可以用两个期权结合来实施。图5即表示有限制帽的对赌协议是如何利用一个约定价格为K的多头买方期权减去一个约定价格为U(这个U相当于限制帽的门槛)的空头买方期权来模拟其价值的。与第一次期权的多头地位不同的是,卖方在第二次期权中是空头的地位(继续我们与金融期权的类比分析,卖方是第二次期权的出售者)。由于这两个期权都非常准确地再现了对赌协议在到期日支付补偿的情况,所以期权组合的价值就等于这个对赌协议在到期日之前任何时候的价值。把这两个期权结合起来,就可以得出对赌协议EO的价值为:

这里Ck是约定价为K的多头期权(第一次期权)的价值,而Cu是约定价为U的空头期权(第二次期权)的价值。当然,如果把更多的多头和空头期权结合起来,还可以评估更复杂结构的情况。
(五)固定的随后支付
第三种付款方式(如图3)的情况就是固定的随后支付。这种情况可对应于一个不连续的两值买权。两值期权是具有不连续收益的期权,一个简单的例子就是现金或无价值的看涨期权。在T时刻,标的资产价格低于门槛值K时,该期权一文不值,而当标的资产价格超过K(执行价格)时,该期权支付一个固定数额Q。此时在风险中性世界里,期权到期时标的价格超过执行价格的概率为N(d2)。如前面所引用的修正的布莱克-舒尔斯方程,可以得出两值期权的价值:

其中,

五、案例计算
这一部分,我们将模型的应用以实际案例来说明。表1给出对赌协议相关的参数,EBIT为企业运营的测试指标值。

表1 案例研究的参数价值
考虑到不同对赌协议条款的变化,对应图1、2、3分别列示的几种情况:
(1)在今后四年每年年末,如果EBIT值超过参考值1000万元(k=1000),则卖方可以从超过部分获得50%的利益。
(2)如果三年以后EBIT值超过参考值1000万元,则卖方可以收到超过部分价值五倍的随后支付。但协议支付上限(支付帽)是1200万元。
(3)如果三年以后EBIT值超过参考值1200万元,卖方可以收到一笔随后的固定额支付1000万元。
下面分别对几种情况进行价值评估。
第一种情况:除开确定的初始支付之外,卖方握有一个四个看涨期权的组合,即根据EBIT值是否超过约定价格K=1000万元可以有50%的分成。对赌协议的价值就等于四项期权价值之和。可以根据方程(12)来进行价值评估,即:

这里,

采用表1中所列出的参数值,分别计算四项期权的价值。
先计算第一年的期权值,即T=1时的X的期望值。根据方程(9),
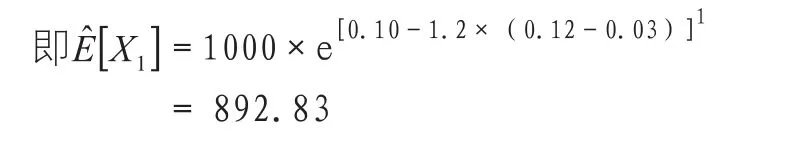
根据公式计算d1和d2:

于是,可以得出第一年末对赌协议期权,即T=1时的价值:

N()可以在正态分布累计概率密度表上查出,也可以在Excel表上用函数NORMDIST查出。第2、3、4年的期权价值可以同样得出。即:
T=2时,期权价值=38.9807
T=3时,期权价值=49.0529
T=4时,期权价值=56.4719
总的期权价值等于上述四个期权价值之和,即:Total= 168.7736。
第二种情况:这种情况类似两个看涨期权的结合。首先,卖家持有一个看涨期权,执行价K=1000万元。由于当EBIT超过约定价的时候,超过部分将会有一个5倍的补偿,所以因子α=5,而支付帽是1200万元。所以卖方还有一个空头的买权(short call),约定价是K=1200万元。当然倍数因子同样是α=5。如果把多头买权(long call)理解为持有买权或买进买权,那么空头买权(short call)就是签发买权或卖出买权,如图5所示。这两种期权的组合正好反映了情况2所示的对赌协议条款结构。期权价值的和就等于对赌协议价值,可以采用前面情况1的同样方法,只不过这里,
α=5;K=1000万元;T=3。
依然采用表1中所列参数值,分别计算两种期权的价值。根据方程(9)求中性风险的期望值:

根据公式计算d1和d2:

于是,可以得出第一个买方期权价值,即:
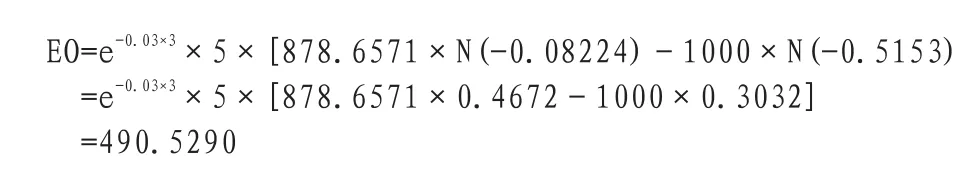
同样方法,得出第二个空头卖方期权价值为-276.9700。
于是,总的价值等于:
Total=490.5290-276.9700=213.5590
第三种情况:这种情况可对应于一个不连续的两值买权。现在K=1200万元,而固定支付额Q=1000万元,即如果三年后的EBIT超过1200 时,则卖方可收到一个1000万元的固定支付款,否则收入为零。
可应用方程(14):
首先求期望值:

然后求d2:

对赌协议能够在买方和卖方之间架设协商的桥梁,因而促进交易的成功。特别是在目标公司未来预测前景高度不明朗的情况下,这样的协议条款能够解决交易双方由于预测的差异、信息的不对称等所造成的分歧。
本文提供了一个对对赌协议期权进行价值评估且容易操作的评估模型以及案例演示,意在抛砖引玉。对于更复杂的协议条款和付款方式,则需要广大评估师在实践中根据具体情况设计出更复杂的期权组合和计算模型。
[1]约翰.赫尔.期权、期货及其他衍生产品(第六版).人民邮电出版社,2009.
[2]理查德.布雷利,斯图尔特.迈尔斯.资本投资与估值.中国人民大学出版社,2010.
