基于半参数变系数部分线性模型的小麦抗倒伏性分析

刘 锋，王利兵，徐振枢

(重庆理工大学数学与统计学院，重庆 400054)

小麦的抗倒伏性受许多外界和内部因素的影响，例如风力大小、种植密度、雨量等。这些指标对于小麦抗倒伏性产生不同情况的影响。但是，小麦自身的抗倒伏性对于小麦生产也至关重要，很多学者研究了农作物抗倒伏性与自身的指标之间的关系［1-5］，例如文献［1］利用通径分析对抗倒伏性进行研究，文献［2］研究了小麦形状与抗倒伏性之间的关系，文献［3］研究了小麦抗倒伏性在小麦生长的不同时期所造成的影响。通过增强小麦的抗倒伏性，可以更有效地让小麦达到成熟，从而增加小麦产量。袁志华等［4］通过力学研究了农作物抗倒伏性，董琦等［5］通过基部茎节形态结构特征对抗倒性进行了研究。

根据资料:

上述公式中茎秆鲜重与茎秆重心高度都是可以通过测量得到的，而机械强度往往不容易获得，因此，茎秆机械强度对于小麦抗倒伏性是非常重要的。

本文研究了小麦的机械强度与小麦自身各指标之间的关系，主要应用半参数变系数部分线性模型来对小麦机械强度与小麦自身各指标参数之间关系进行研究，从而建立机械强度(Ms)和小麦自身各指标之间的模型，提高小麦的机械强度(Ms)，增强小麦的抗倒伏性。

1 半参数变系数部分线性模型估计

1.1 半参数变系数部分线性模型

半参数变系数部分线性模型的具体形式是:

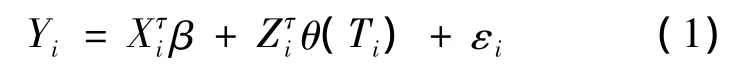
显然模型(1)包含了许多通常的参数、半参数和非参数模型，例如:当θ(·)=θ(其中θ是一个常向量)时，模型(1)退化成为一个线性度模型;当q=1，z=1时，则模型(1)退化为部分线性模型。

1.2 模型估计方法

对于模型(1)，需要对未知参数和未知函数部分进行估计。模型(1)有很多种估计方法，Zhang等［6］将模型分成线性部分和非线性部分，用两部估计的方法得到参数与非参数的估计，并且证明了它们的最优收敛速度;Li等［7］用核函数和最小二乘的方法得到了参数与非参数的估计;Fang和Huang［8］用profile最小二乘方法得到了非参数的估计;Zhou和You［9］用最小二乘和经验似然方法得到了参数与非参数的估计。

本文结合最小二乘估计和非参数估计的方法，得到参数 β =(β1，β2…βp)和非参数函数θ(·)=(θ1(·)，θ2(·)…θk(·))的估计。

对于任意给定的 β =(β1，β2…βp)，则模型(1)可以写成

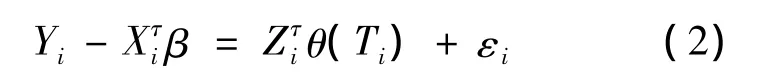
或者

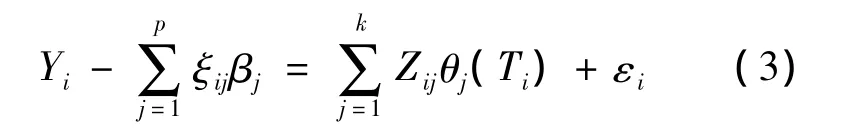
则模型(1)成为一个变系数模型，可应用局部线性回归技术估计函数。

对于任意给定的T0，局部线性趋近θ(T0)，泰勒展开θj(T)得到:

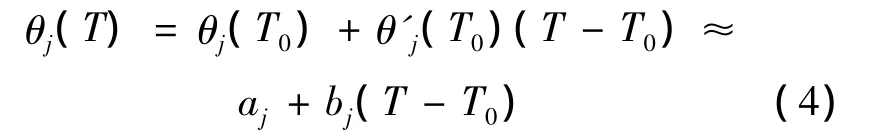
应用权局部最小二乘法来找到 aj，bj，j=1，…，k，即极小化下式:

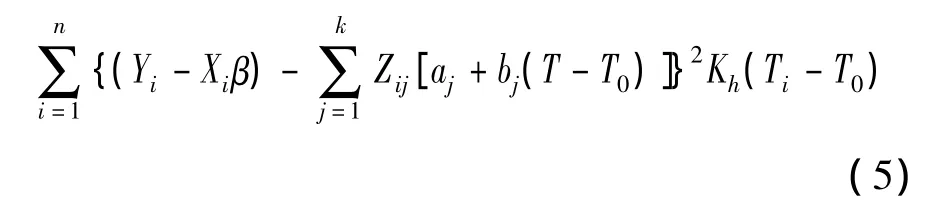
其中:Kh(·)=K(·/h)h是任意给定的核函数;K(·)是任意的核函数;h是带宽。

令

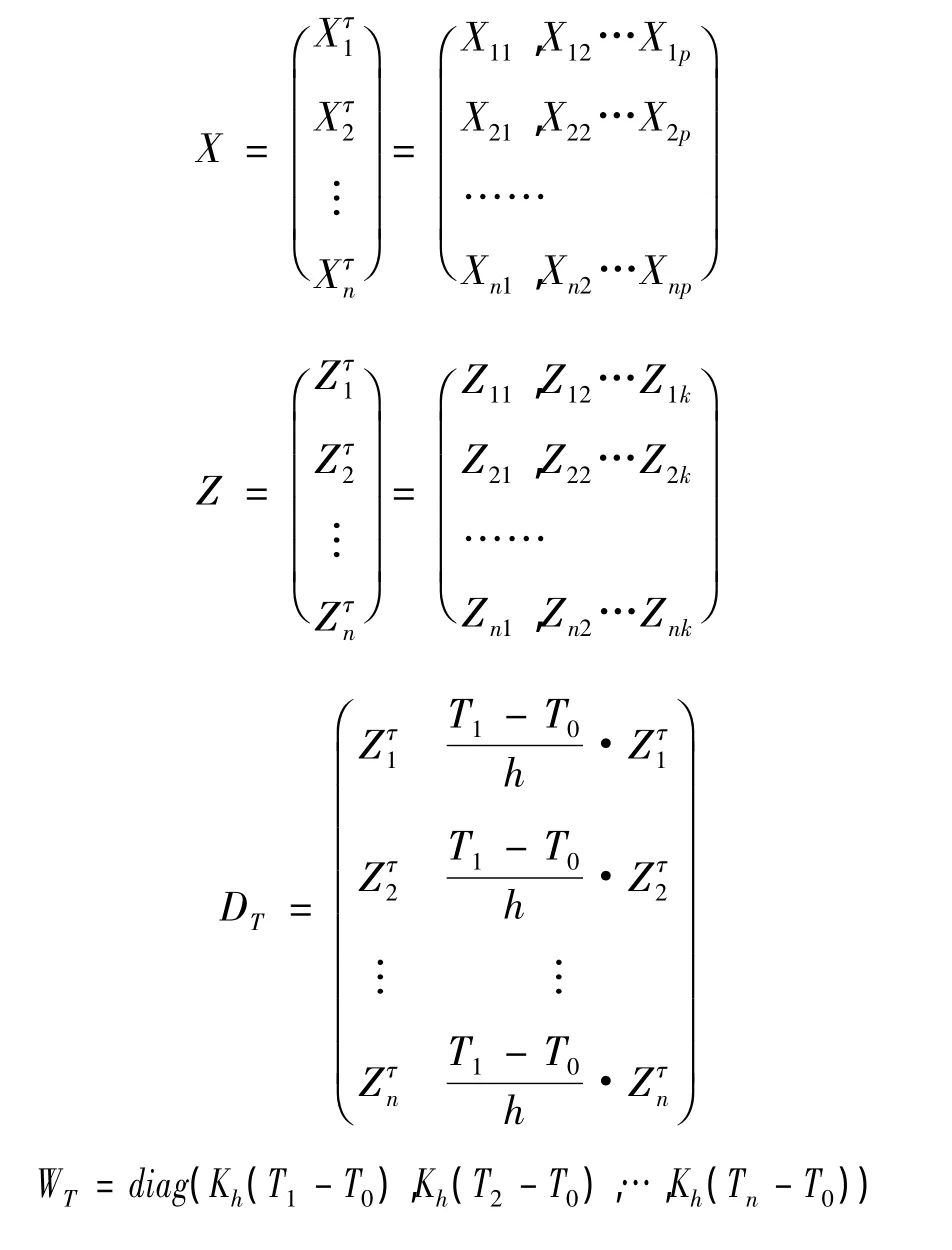
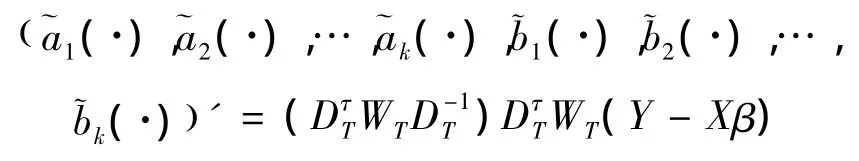
因此

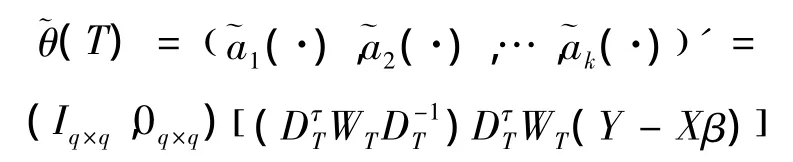
令

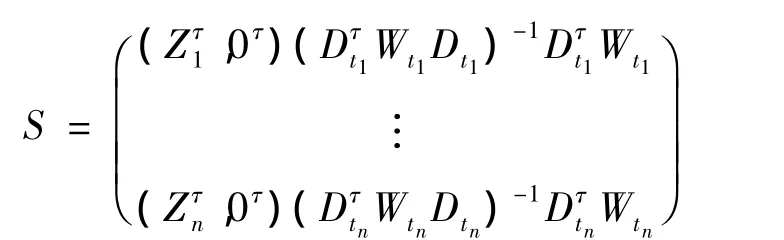
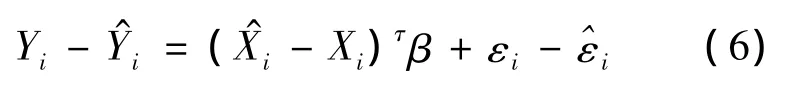
其中:

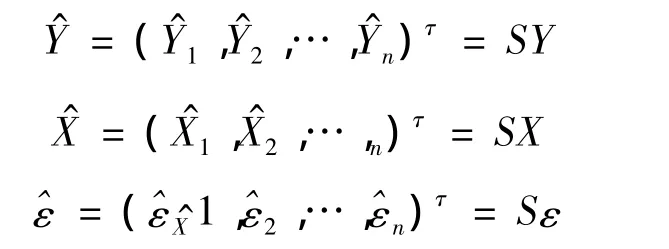
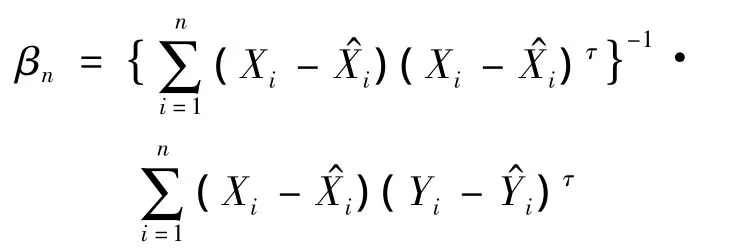
1.3 缺失数据分析

缺失数据在日常生活和科研中是常常遇到的，由于某些原因，使得原本完整的数据变成了缺失数据。分析中只能采用部分数据，而不能选用所有的数据。

对于缺失数据的分析，首先设定缺失指示变量，即

本研究是自变量的数据缺失，采用文献［7］中所使用的方法，借补估计:

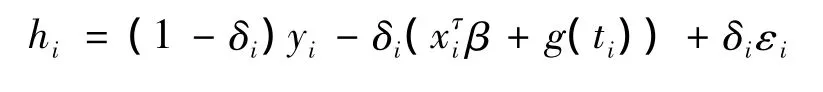
从而得到模型的借补值。

2 数据与实证分析

2.1 数据的选取

数据来源于2011年全国研究生数学建模数据c题，本文选取2007年矮抗58品种小麦的几个不同时期生理指标作为研究对象，包括小麦各节长度、粗度，单个小麦的重心高度、茎秆壁厚、穗重等对小麦抗倒伏性研究较为重要的指标。

2.2 数据分析

2.2.1 矮抗58乳熟期分析

首先选取一些指标，令:y为机械强度;x1为茎秆重心;x2为基部第5节长度;x3为基部第5节粗度;x4为基部第4节长度;x5为基部第4节粗度;x6为基部第3节长;x7为基部第3节粗度;x8为基部第2节长度;x9为基部第2节粗度;x10为茎秆壁厚;x11为麦穗鲜重。

对于以上指标，有些显然有很强的相关性，那么就需要降维。本文采用因子分析方法。

由于存在不确实数据，需要用本文1.3节方法进行借补，然后进行相关性分析。之后对数据进行标准化，得到了如表1所示的相关系数矩阵。

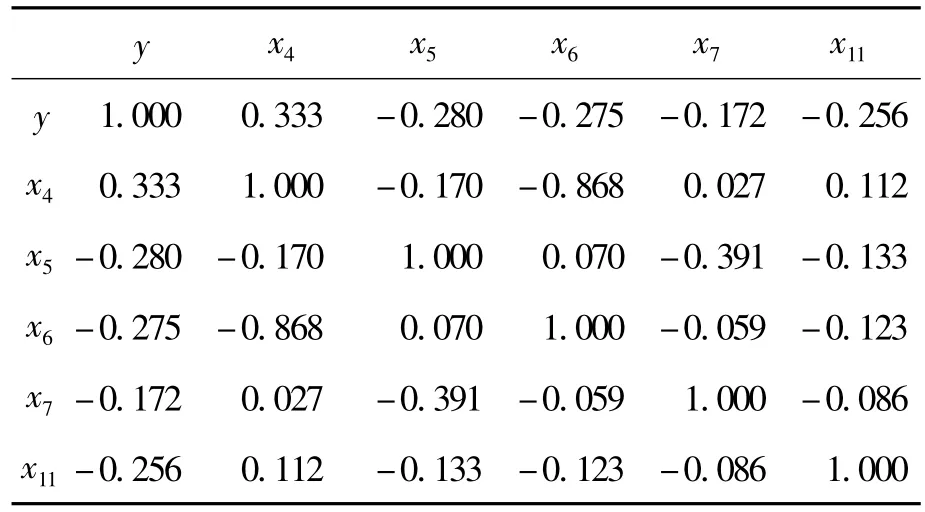
表1 矮抗58机械强度与主要指标之间的相关系数矩阵

从表1可以看出，这些指标之间存在着很强的相关性，因此通过因子分析进行降维。通过数据模拟，得到前3个成分的累积贡献率达到86.369%，取这3个成分进行分析，具体形式为 :

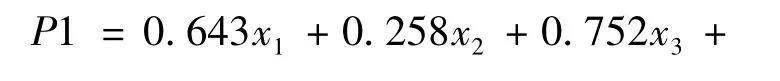
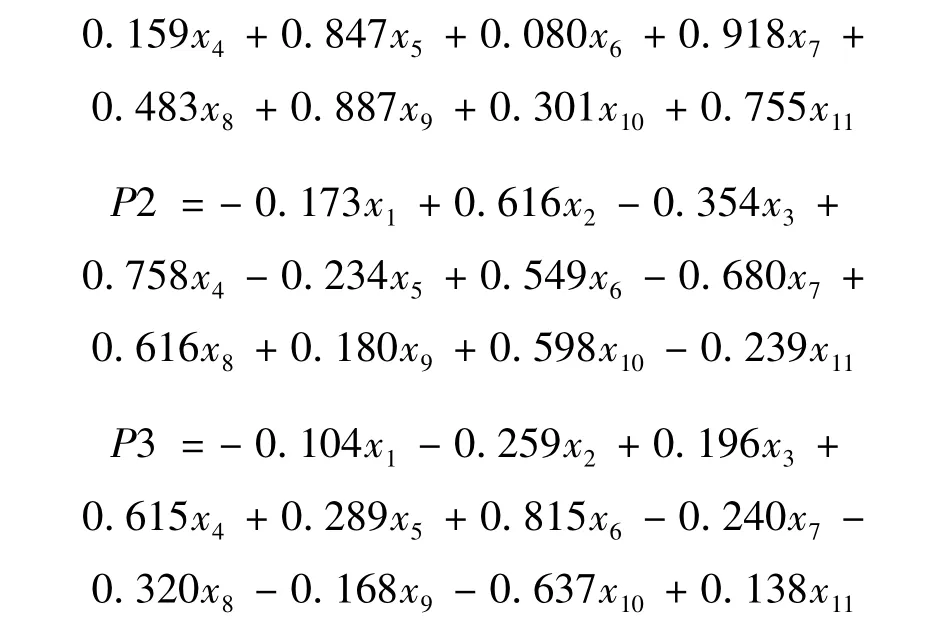
将得到的3个成分与小麦机械强度作散点图，见图1～3。

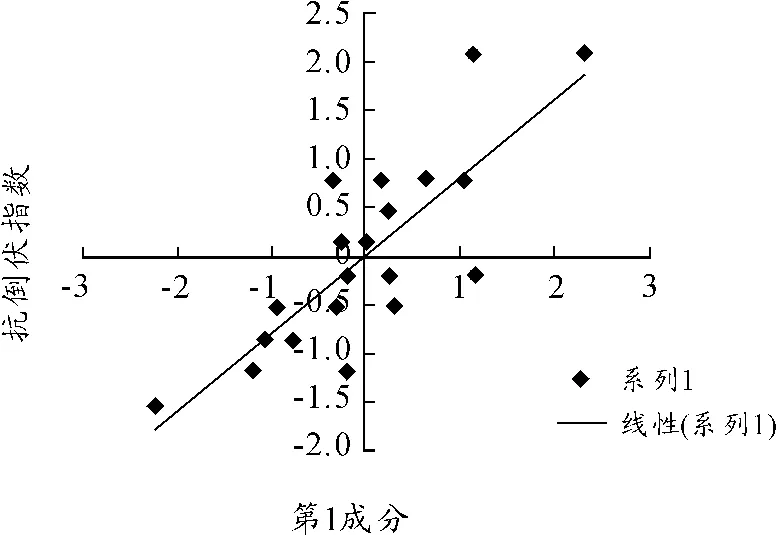
图1 矮抗58第1成分与机械强度之间关系

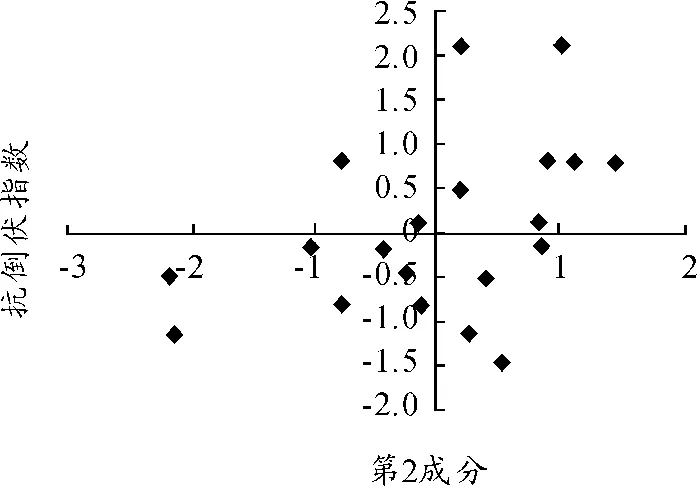
图2 矮抗58第2成分与机械强度之间关系

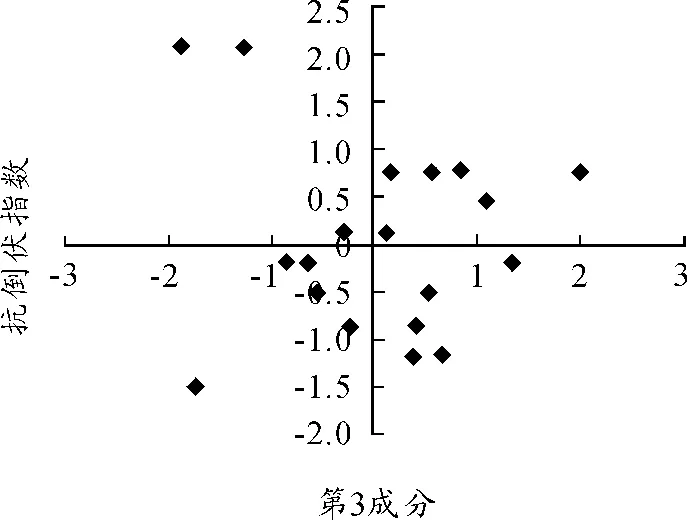
图3 矮抗58第3成分与机械强度之间关系

从图1～3可以看到，小麦机械强度与第1成分有较为明显的线性关系，而第2、第3成分与小麦机械强度之间没有具体的函数形式。

采用半参数变系数拟合数据，核函数选取为k(t)=15·(1-t2)2/16，窗宽选择为 h=0.549 280 3，得到拟合方程为

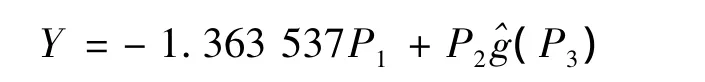
将y的真实值与估计值比较，如图4所示，其中实线代表真实值，虚线是估计值。从图4可以看出大部分估计值符合实际情况。对于一些突出的点，由于源数据存在奇异情况，可以忽略。

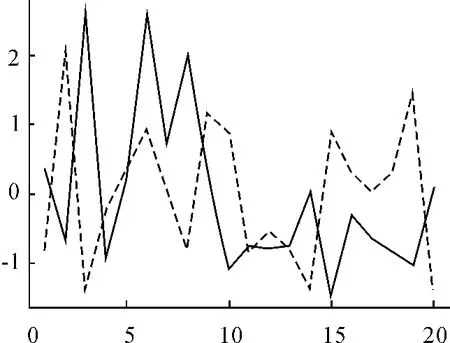
图4 y的真实值与估计值的比较

2.2.2 矮抗58开花期分析

下面分析开花时期的数据。与以上分析相同，首先得到如表2所示的相关系数矩阵。

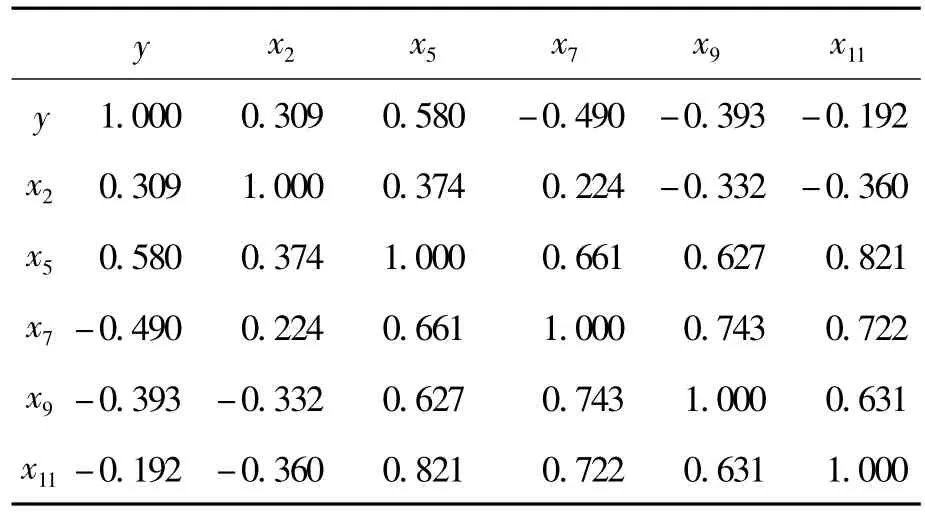
表2 矮抗58开花期强度与主要指标之间的相关系数矩阵

同样，采用因子分析的方法得到小麦品种矮抗58的机械强度与各个指标之间的关系。通过数据模拟，前3个因子组合的贡献率达到了79.241%。取这3个成分为主成分，进行进一步分析，具体形式为:

可以得到3个成分与小麦机械强度之间的散点图，如图5～7所示。

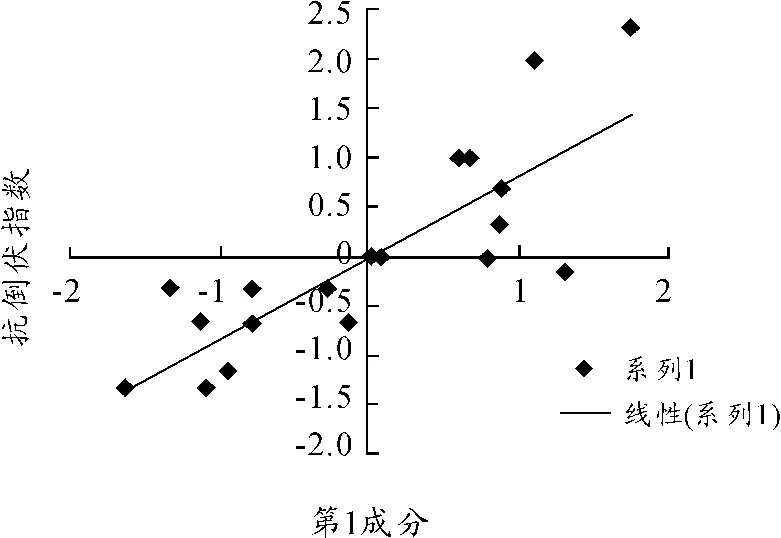
图5 矮抗58开花期第1成分与机械强度之间关系

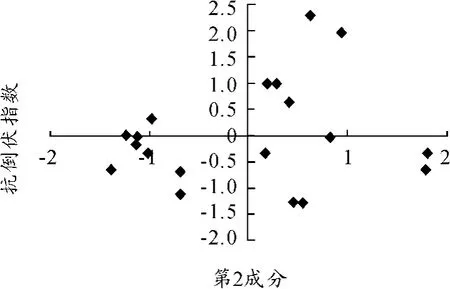
图6 矮抗58开花期第2成分与机械强度之间关系

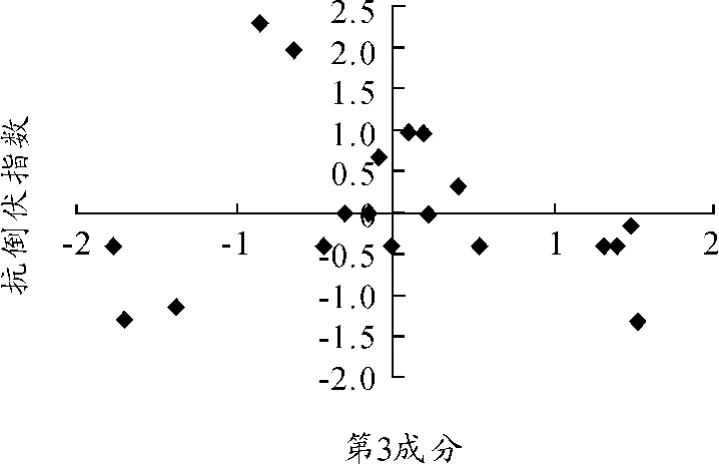
图7 矮抗58开花期第3成分与机械强度之间关系

由图5～7可以看出，矮抗58小麦机械强度与第1成分是线性相关的，而与第2成分是无法得到具体函数形式的。这里核函数选取为

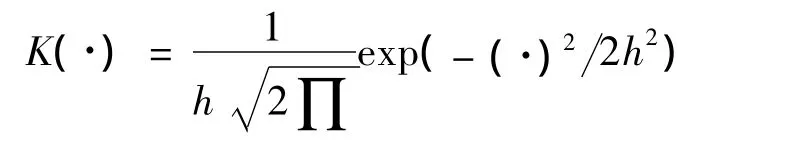
窗宽选择为h=0.554 944 2。

应用非参数最小二乘估计，得到如下拟合方程:

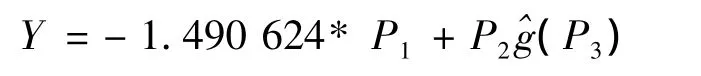
将真实值与估计值进行比较，结果见图8。其中实线代表真实值，虚线是估计值。

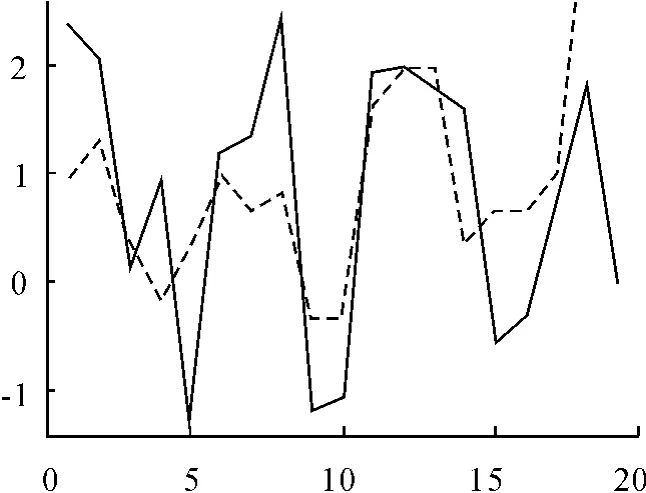
图8 真实值与估计值模拟比较

由此可以得到各个时期的小麦的机械强度与小麦自身之间的关系。

同样利用此方法也可以得到2008年与2011年的另外两个小麦品种在这两个年度中样品的平均机械强度(机械强度的平均值)，参见表3。

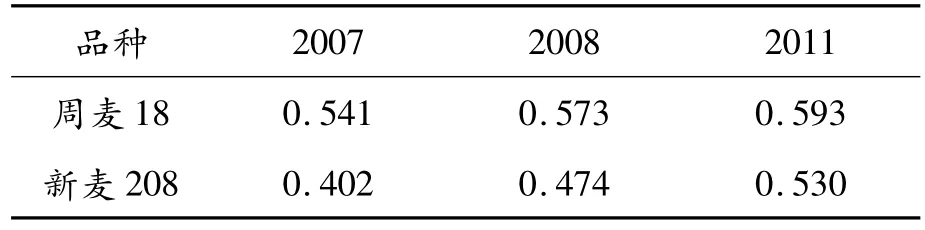
表3 3个年度2个小麦品种机械强度 kg

3 结束语

本文将半参数变系数部分线性模型应用到小麦抗倒伏性的研究中，获得了对小麦抗倒伏性起到关键作用的机械强度指标的计算方法，得到的矮抗58小麦的抗倒伏性结果，对于今后小麦的抗倒伏性研究有一定的指导意义。

本文还有以下问题还需要进一步研究:首先，由于数据给定的范围较为有限、样本量有限等，模型的精度还有待进一步的提高;其次，选用模型的估计方法是最小二乘估计，这种估计方法对于边界值的处理一般存在偏差，这也是为什么模拟的边界值都存在很大的差异;最后，得到的数据很多是存在歧义的，虽然做了一些简单的处理，但是结果不是很理想。

［1］田保明，杨光圣，曹刚强.农作物倒伏及其影响因素分析［J］.中国农学通报，2006，22(4)：163-167.

［2］王勇，李斯深，李安飞，等.小麦种植抗倒性的评价和抗倒性装的相关与通径分析［J］.西北植物学报，2000，20(1)：79-85.

［3］余泽高，李志新，严波.小麦茎秆机械强度与若干形状的相关性研究［J］.农业工程学报，2007，23(7)：14-18.

［4］袁志华，冯宝萍，赵庆安，等.作物茎秆抗倒伏的力学分析及综合评价探讨［J］.农业工程学报，2002，18(6)：30-31.

［5］董琦，王爱萍，梁素明.小麦基部茎节形态结构特征与抗倒性的研究.［J］.山西农业大学学报，2003，23(3)：188-191.

［6］Zhang W，Lee W J，Song X.Local polynomial fitting in semivarying coefficient models［J.］J Multi Anal，2002，82：166-188.

［7］Li Q，Huang C J，Li D.Semiparametric smooth coefficient models［J］.J Bus Econ Statist，2002，3：412-422.

［8］Fan J，Huang T.Profile likelihood inferences on semiparametric varying-coefficient partially linear models，Manuscript［D］.Chapel Hill，USA：University of North Carolina，2002.

［9］You Jinhong.Gemai ChenEstimation of a semiparametric varying-coefficientpartially linear errors-in-variables model［J］.Journal of Multivariate Analysis，2006，97：324-341.