基于年龄分布和加权总规模的竞争系统的适定性

于晓娣，雒志学，李 晶，巴争刚

(兰州交通大学数学系，兰州 730070)

1 模型

在基于年龄结构的2种群适定性问题的数学模型的建立方面已有不少研究成果［1-6］，而大多数学者在系统建模时假设:不同年龄的个体对种群发展具有相同的影响，这显然不符合实际情况。本文将其影响因素考虑在内，所研究的系统模型如下:

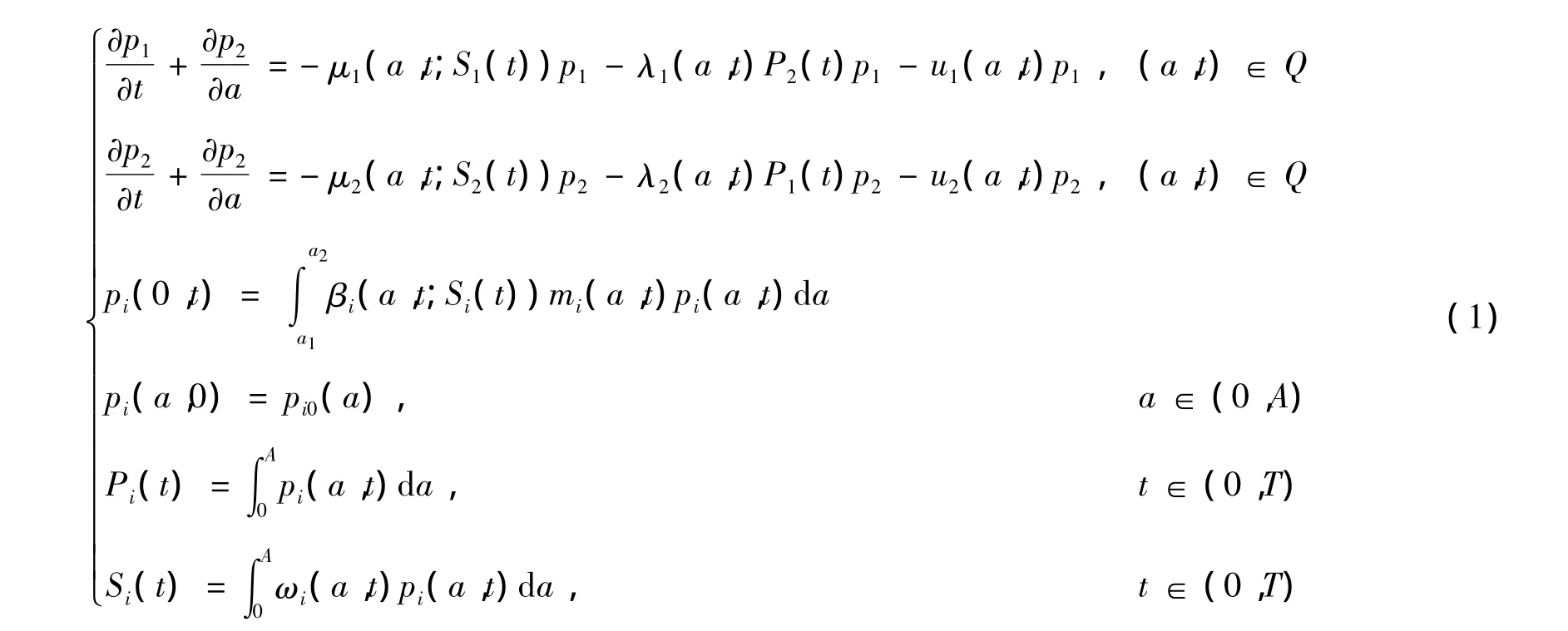
其中:Q∈(0，A)×(0，T)，A、T分别表示个体最大年龄和控制周期0＜A＜+∞;假设2种群具有相同寿命，［a1，a2］是雌性生育区间;pi(a，t)为第i个种群在t时刻年龄为a的种群个体数量;λi(a，t)为种群间作用系数;mi(a，t)为第i个种群雌性比率，0＜mi(a，t)＜1;pi0(a)为第i个种群初始年龄分布;Si(t)为第i个种群在t时刻的加权总量;ω为权函数;μ、β为出生率和死亡率;ui(a，t)为人类对种群个体的收获努力度，是本文的控制变量，满足:

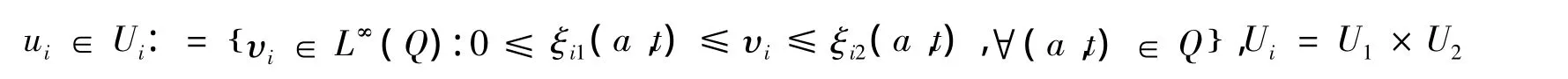
本文假定下列条件成立(i=1，2):

(H1)对于∀(a，t;xi)∈Q ×［0，+∞］，μi(a，t;xi)≥0，固定(t;xi)+∞，μi关于xi局部Lipschitz连续。

(H2)对于 λi∈L∞(Q)，0≤λi(a，t)≤λ，λ 为常数，a.e.(a，t)∈Q。

(H3)当 a ＜a1或 a ＞a2时，βi(a，t;Si(t))≡0，且0≤mi(a，t)≤M0，M1为常数，a.e.(a，t)∈Q。

(H4)对于∀(a，t;xi)∈Q ×［0，+ ∞)，0≤βi(a，t;xi)≤M1，M1为常数，βi关于 xi局部 Lipschitz连续。

(H5)∀(a，t)∈Q，0≤ωi(a，t)≤M2，M2为常数;∀a∈(0，A)，0≤pi0(a)≤M3，M3为常数。

定义1 系统1的解L∞(Q;R2)，i=1，2满足

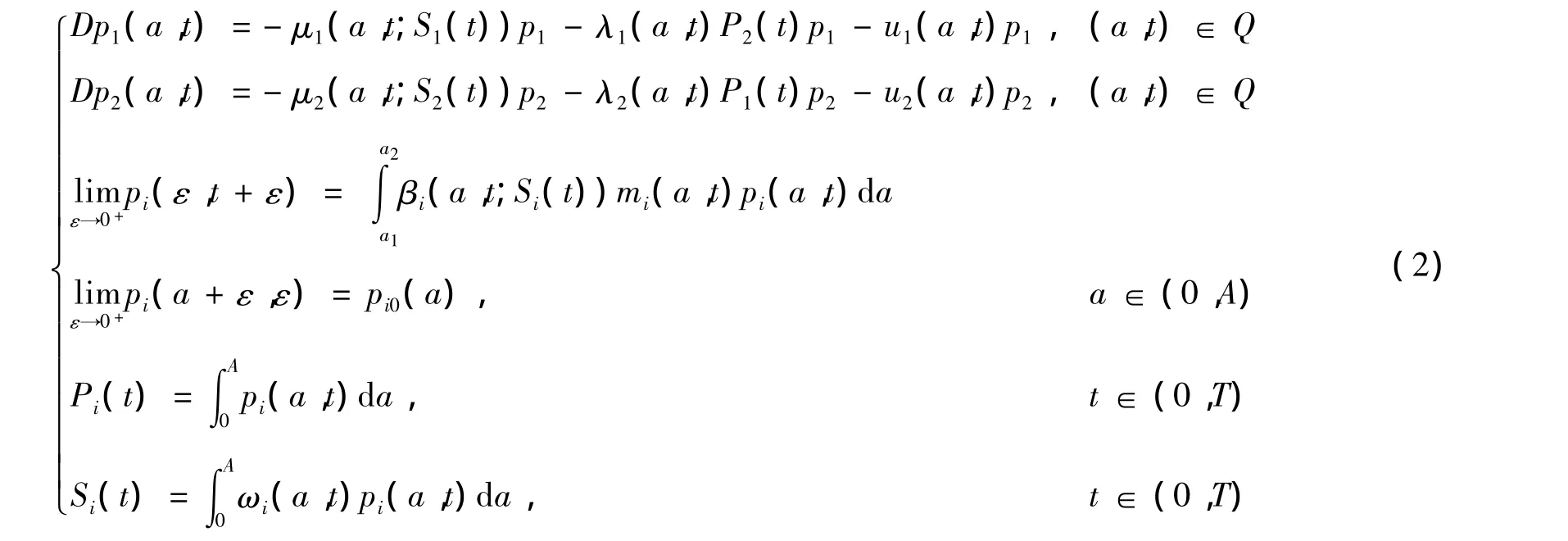
2 模型的适定性

对于任意固定的 υ =(υ1，υ2)∈L∞(Q;R2)，υi(a，t)，定义，考虑系统

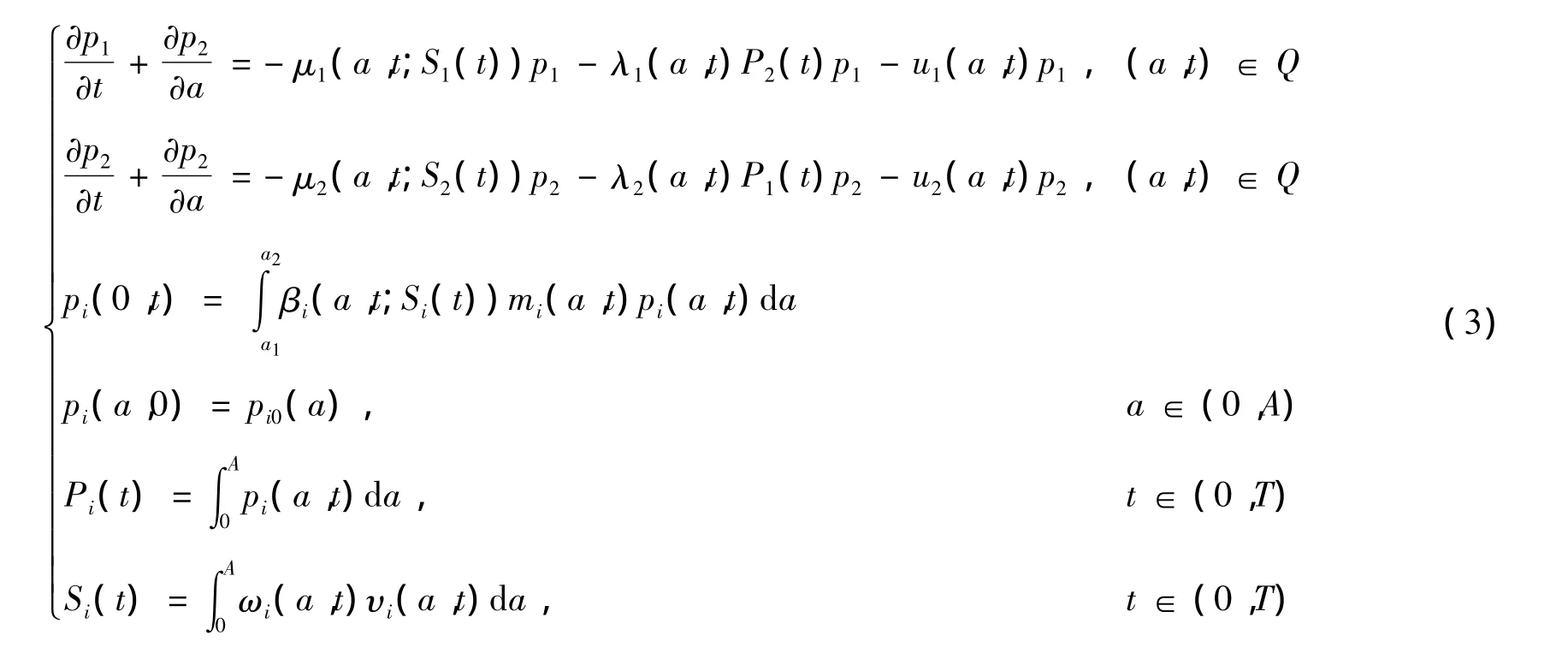
系统(3)具有唯一非负解，且 p=(p1，p2)∈L∞(Q;R2)，pi(A，t)=0，∀t∈［0，T］，i=1，2。由特征线法，得到系统(3)的解:

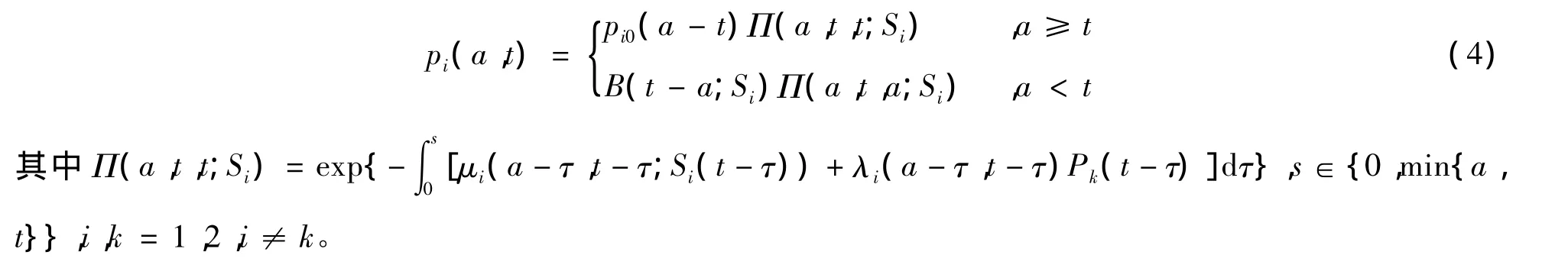
B(t;Si)为下列Volterra积分方程的解:

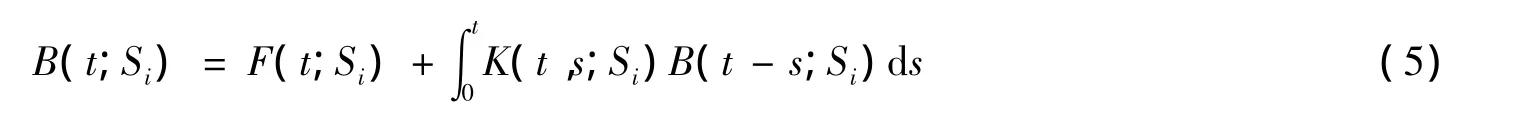
其中:

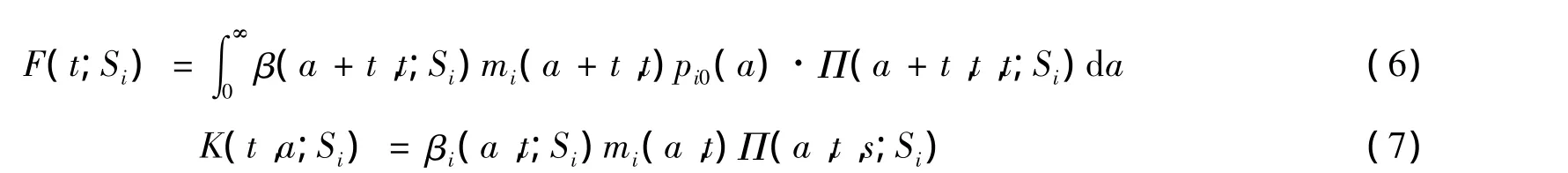
上述表达式中，函数pi0、βi、Π在其定义域外延拓为零。

本文假设T＞A，令

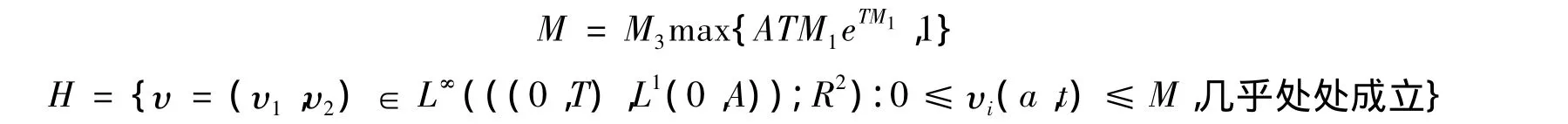
对于 υ(i)=(υi1，υi2)∈H，记系统(3)相应的解为 p(i)=(pi1，pi2)，x=(x1，x2)=p(1)-p(2)，i=1，2。

引理1 存在正常数 C1、C2、C3，使得对任意 υ(1)=(υ11，υ12)，υ(2)=(υ21，υ22)∈H 及任意 t∈(0，T)，有

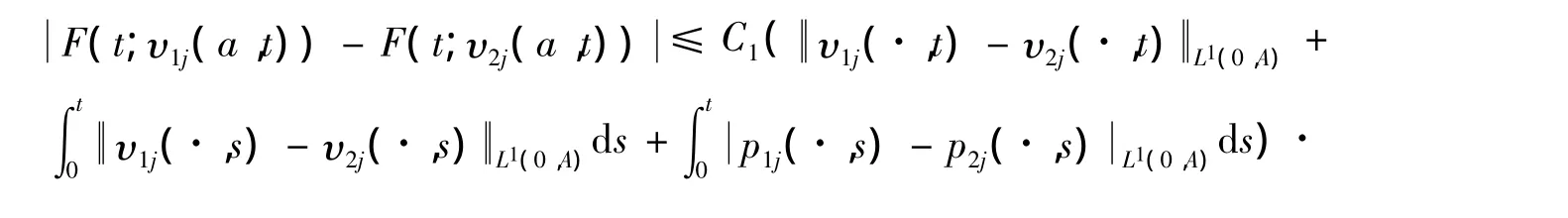
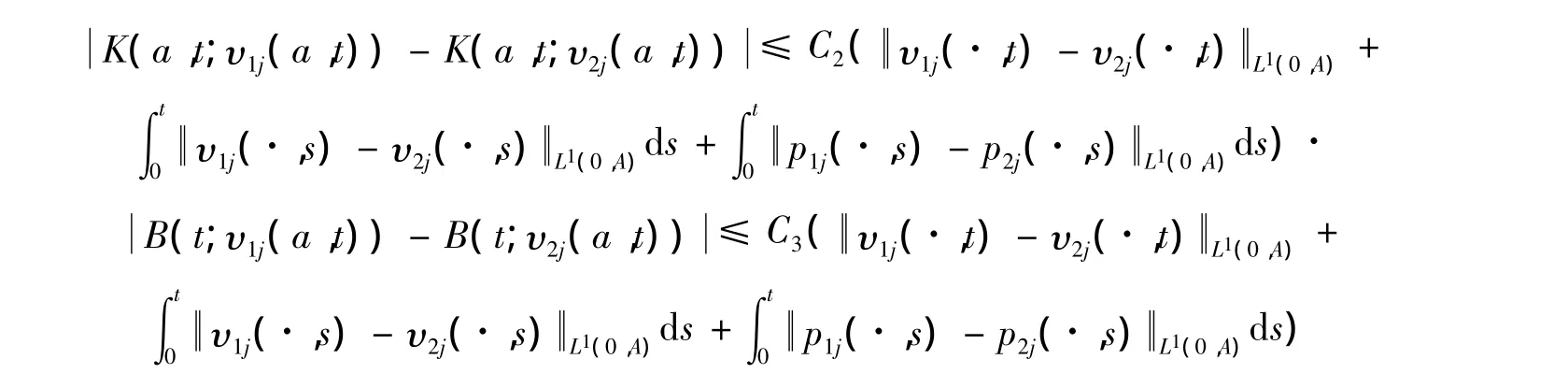
证明

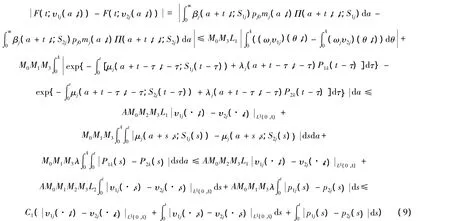
其中

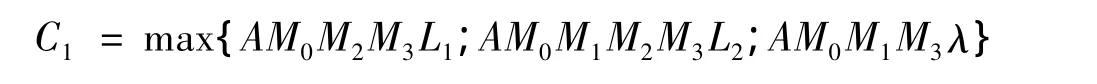
同理可得:

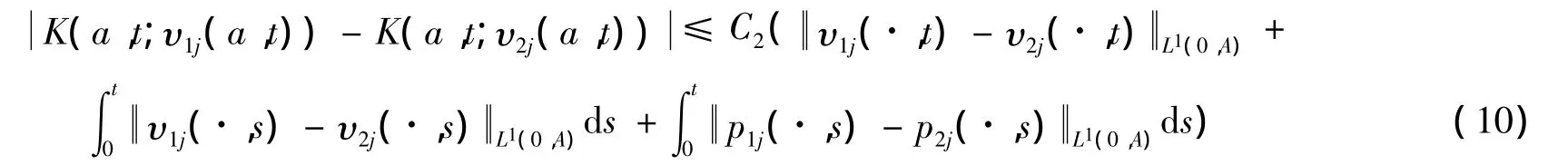
其中 C1=max{M0M2L1;M0M1M2L2;M0M1λ}。

由式(5)～(7)得:

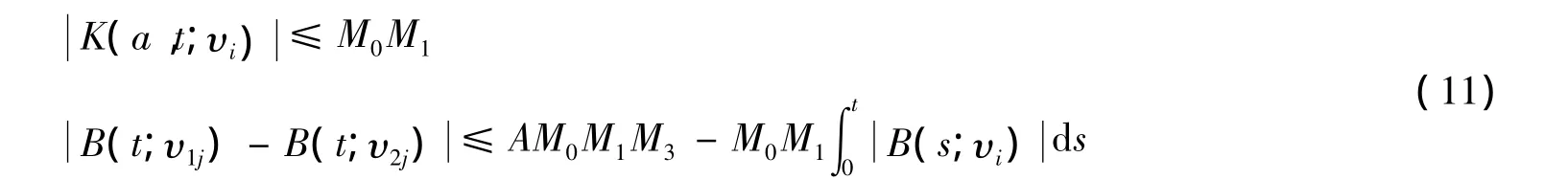
由Bellman引理可知:

由式(5)，(9)～(12)可知:

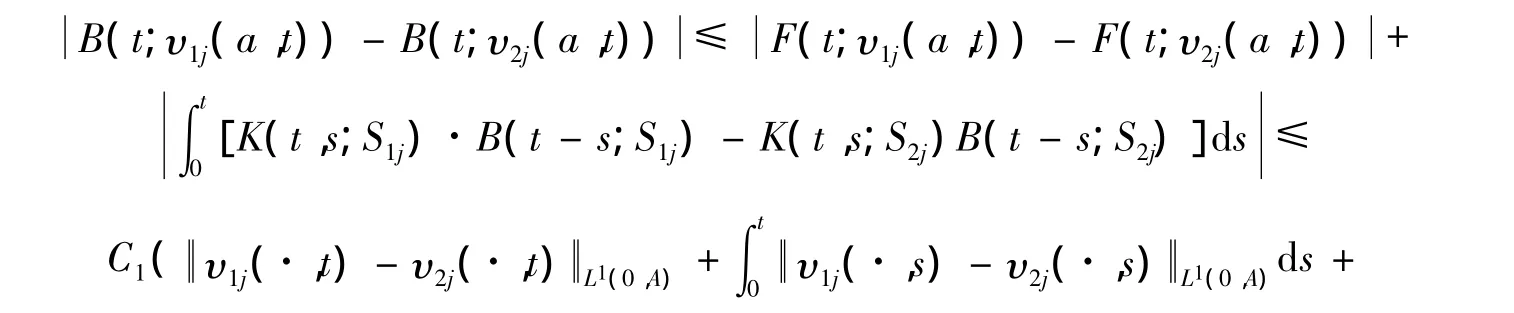
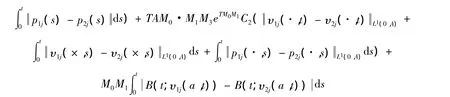
再根据Gronwall引理得:

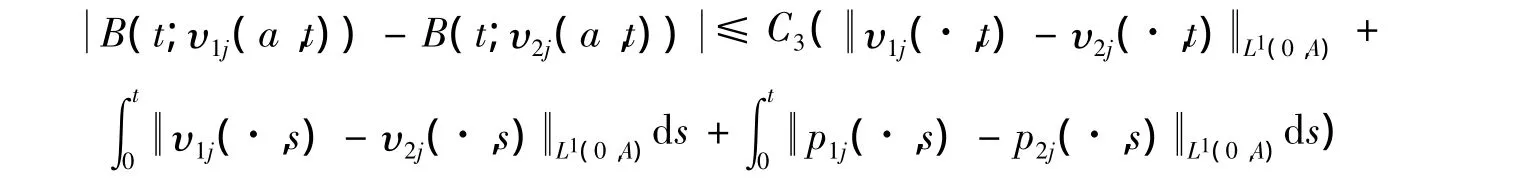
其中:

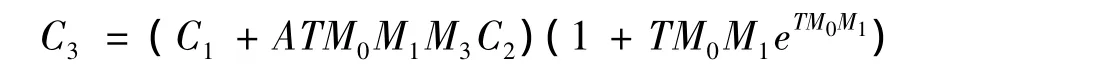
引理2 存在正常数C使得对任意υ(1)，υ(2)∈H，有

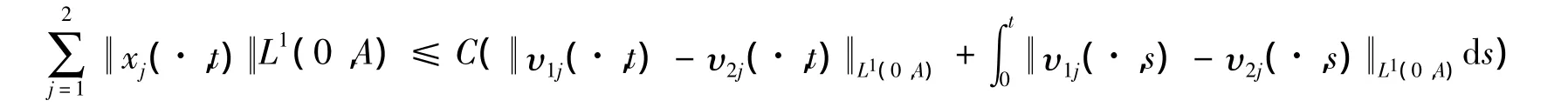
证明由式(4)和引理1得

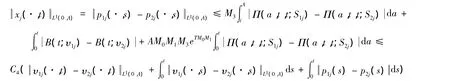
其中:

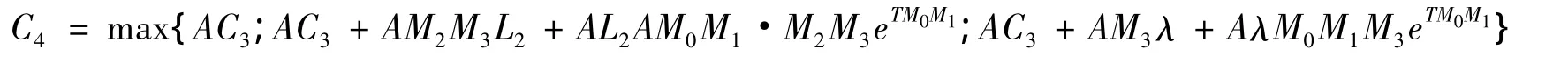
则

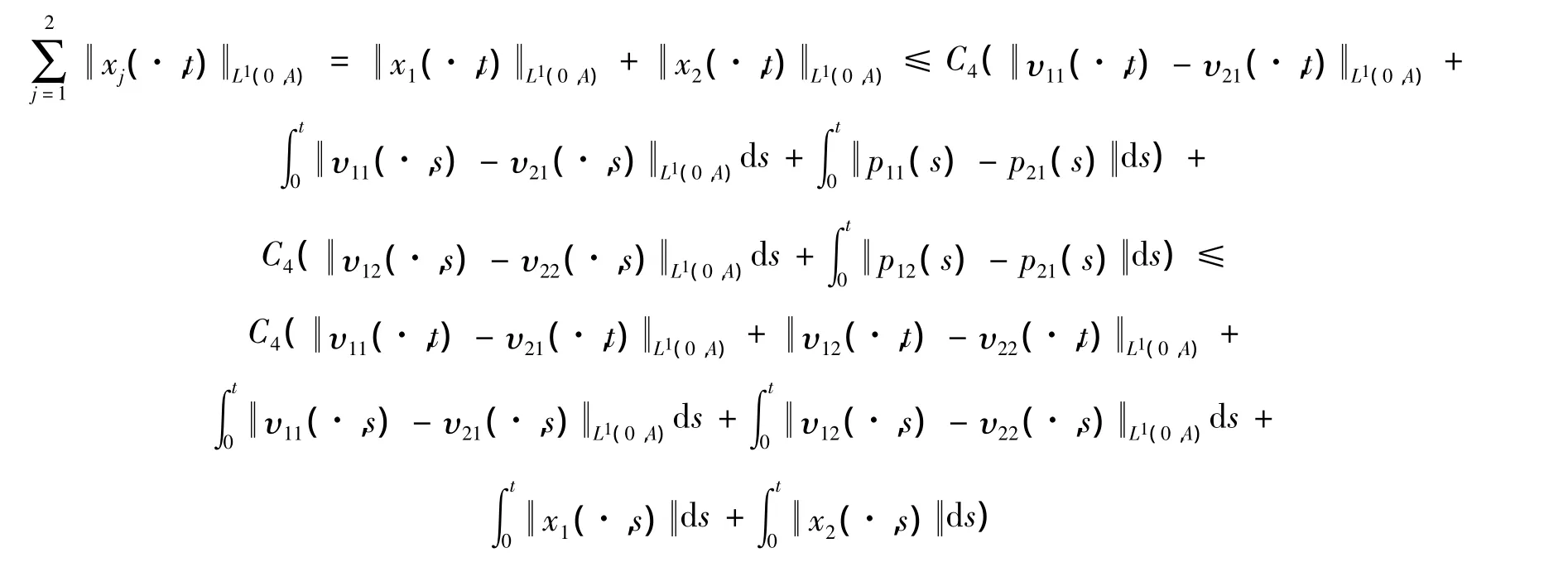
由Gronwall引理得:

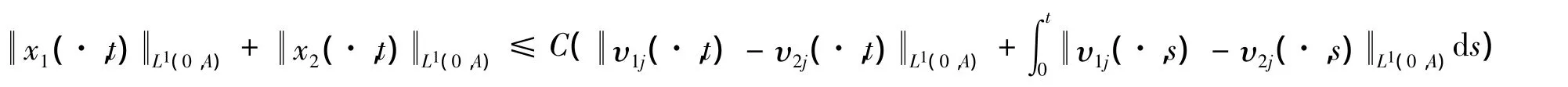
其中C=C4(1+TeTC4)。

定理1 任意给定u∈U，系统(1)存在唯一解pu满足:① pu∈L∞(Q;R2);②;③ pu连续依赖于u。

证明定义映射 G:H→H，Gυ(a，t)=pυ(a，t)，∀(a，t)∈Q，以及一个等价范数:

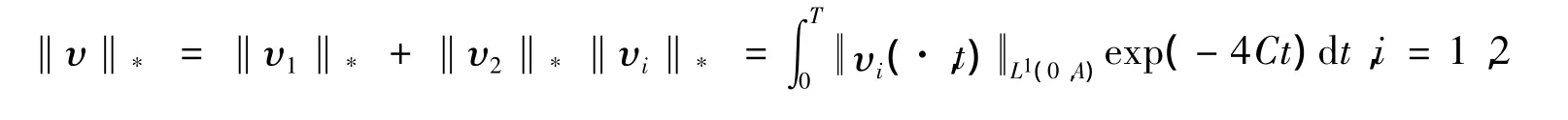
利用引理2得:

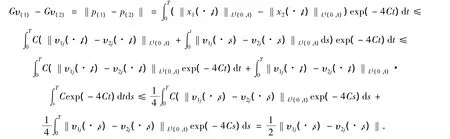
因此G是空间上的(H，‖·‖*)压缩映射，存在唯一点υ*，它就是系统(1)的解。

取 ui=(ui1，ui2)∈U，令

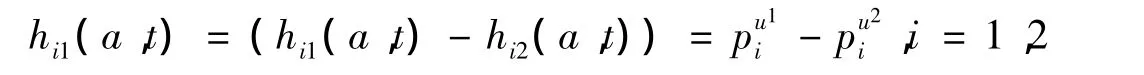
则可以得到:

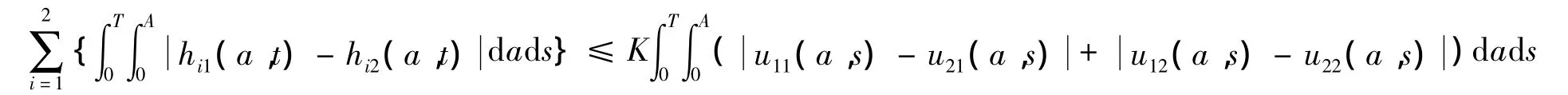
其中K是常数。上式意味着pu关于u连续。

［1］He Zerong.Optimal birth control of age-dependent competitive species［J］.J Math Anal Appl，2004，29(6)：286-301.

［2］He Zerong.Optimal Harvesting for an Age-strucred Predator-prey System［J］.Mathematica Applicata，2006，26(4)：467-483.

［3］雒志学.具有年龄结构的捕食-食饵种群动力系统的最优收获控制［J］.数学的实践与认识，2007，37(12)：115-120.

［4］Luo Zhixue，Guo Jinsheng.Optimal harvesting for three competing species with age-dependent and diffusion［J］.Advances In Mathematices，2009，38(2)：209-219.

［5］Anita S.Analysis and Control of Age-Dependent population Dynamics［M］.Dordrecht：Kluwer Aca-demic Publishers，2000.

［6］孙宏雨，赵春.具有年龄结构两竞争系统的适定性和最优控制［J］.应用数学学报，2010，33(6)：1037-1048.

［7］何泽荣，朱广田.基于年龄分布和加权总规模的种群系统的最优收获控制［J］.数学进展，2006，35(3)：315-324.

［8］孙宏雨，赵春.具有年龄结构三竞争系统的适定性［J］.天津师范大学学报，2011，31(2)：1-5.