一种基于博弈论的无线网状网络信道分配算法

郑鹏宇，何世彪，张馨月，黄 帅

(1.重庆通信学院，重庆 400035;2.中国烟草总公司重庆市公司石柱分公司，重庆 409100)

无线网状网(wireless mesh network，WMN)是由组织成网状的无线节点构成的通信网络，具有自组织、自配置、低开销、自愈性以及高带宽等优点。鉴于这些优点，WMN具有许多重要的商业应用，如“社会无线网络”“应急通信”等。

现在研究的热点集中于多天线多信道(multi-radio multi-channel，MRMC)WMN网络上。多天线多信道无线Mesh网络是由若干配置了多个IEEE802.11 标准天线［1-3］的网状节点构成的，在MRMC网络中节点可以和邻居同时发送和接收数据。

影响MRMC网络性能的因素主要是同信道间的干扰。这种干扰产生的主要原因是邻近节点在同一时间内使用相同的信道传输。信道分配的目的就在于通过将可用的正交信道分配至每一条链路，在保证链接的条件下，使得干扰最小。

本文采用博弈论的方法来解决无线Mesh网络中信道分配的问题。博弈论主要研究多个自主实体之间为了达到某种目的而相互作用的输出结果。而无线Mesh是一个分布式、自组织以及自配置的网络，这些特点就使得每个分布式的节点都可以被视为一个自主实体，这样博弈论就非常适合于解决无线Mesh网络中信道分配的问题。

本文提出了一种基于博弈论的无线Mesh网络信道分配算法。

1 无线传播和干扰模型

在理论分析当中，通常使用的传播模型为圆盘传播模型(two-ray ground模型)，该模型可以描述节点的信号传输范围和载波侦听的范围(干扰距离)。用Rt表示数据最大传输距离，Ri表示载波侦听距离，其关系为Ri=qRt(q≥2)。

无线信道的广播特性导致了同信道邻近节点之间的干扰。文献［4］总结出了3种干扰模型:PCA(primary conflict avoidance)、RCA(receiver conflict avoidance)和TRCA(transmitter-receiver conflict avoidance)，其中TRCA是最为严格的干扰模型，在干扰范围内所有的节点都无法通信。

在如图1所示的圆盘传播模型(q=2)和TRCA干扰模型中，任意一对接点通信时会对同信道的邻近节点造成干扰。图1中，节点A和节点B通信时会对周围16个节点造成干扰，因此，单信道网络的通信效率很低。图1中还显示，在同一信道下，节点C和节点D通信必须和使用相同信道通信的节点A和B相隔3倍Rt才不会产生干扰。

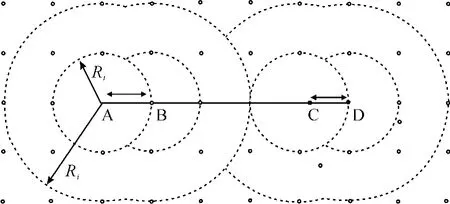
图1 TRCA干扰模型和Two-ray Ground传播模型

2 博弈论建模

2.1 博弈论模型

利用博弈论对无线Mesh网络进行研究，其中的关键是如何将博弈论引入到相应算法的设计与分析之中，找到算法的纳什均衡点［5］。因此，在利用博弈论信道分配问题之前，首先将所研究的问题抽象成博弈论问题模型，无线Mesh网络中的频谱分配问题是关系到各节点频谱选择的博弈过程。假设把频谱的分配等同于信道的分配，即信道分配问题可以建模成一个博弈输出。在这个博弈过程中，无线Mesh网络中的节点可视为参与者，对于传输信道的选择就是行动策略，且参与者的效用与所选择的信道相关联。那么，频谱分配问题的博弈论数学描述的一般形式为

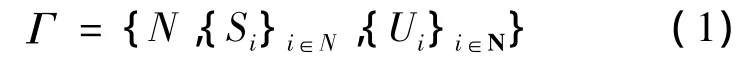
其中:N是参与者(选择某个信道传输数据的无线Mesh节点)的有限集;Si是相对于参与者i的策略集，定义S= ×Si，i∈N是策略空间，则Ui:S→R是效用函数集。在博弈中效用函数Ui是参与者i选择策略si和其对手所选策略s-i的函数。

博弈论分析的关键问题之一是判断对于自适应的信道分配算法是否存在收敛点，且这个收敛点对于任何用户都不会偏移，也就是纳什均衡。因此，对于参与者的一组策略，S={s1，s2，…，sN}，当且仅当 Ui(S)≥Ui(s'i，s-i)，∀i∈N，s'i∈Si时，这组策略是纳什均衡。

2.2 效用函数的确定

通过为每条链路合理地分配信道来达到最大化网络信噪比的目的。而链路能否成功传输数据与网络中的干扰有着密切的联系，即与信噪比SINR有关。因此，在接收端j关于发射端i的信噪比记为SINRre，表达式为

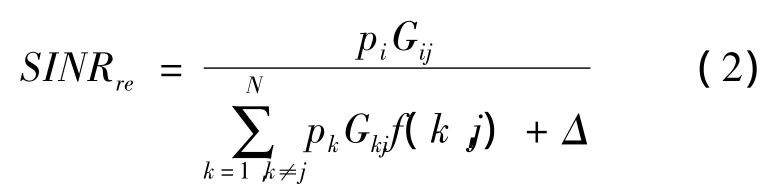
式中:pi是发射端i的发射功率;Gij为发射端i到接收端j的链路增益;Δ 是背景噪声［6］;f(k，j)是表示由节点k到接收端j的干扰方程，其表达式为

可见WMN网络中总干扰最小就是使得网络中各个节点所受到的干扰最小，但节点之间在相同频谱上的干扰又是相互的，这也正符合了博弈论研究问题的特征。

在通常情况下，参与者i能够通过感知在某个特定信道上的干扰来选取最佳的信道传输数据。另一方面，由于网络中参与者之间的干扰是相互的，参与者i所选取的对自身干扰最小的信道并不能保证其对邻近的参与者也是最小的，同时不能保证整个网络的总干扰水平最小。因此，还必须保证参与者i所选取的信道对于其他邻近参与者的干扰最小。定义参与者i效用函数表达式为

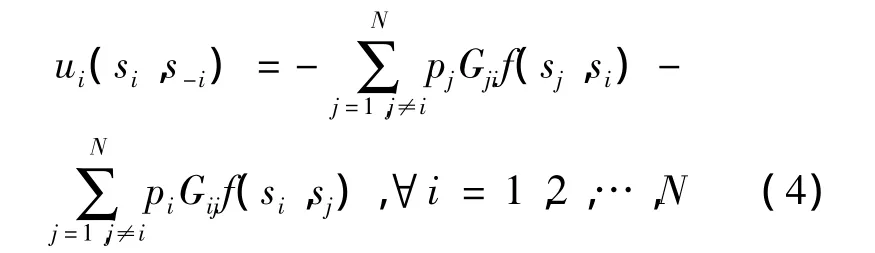
干扰方程为

式(4)、(5)中:P={p1，p2，…，pN}是 WMN 网络中各个节点的发射功率集合(N为节点数);S={s1，s2，…，sM}是策略集(M为正交信道数量)。式(4)中:第1部分是参与者i受到其邻近参与者在相应信道上的干扰，记为Iid;第2部分为参与者在相应信道上对其他邻近参与者的干扰，记为Iod。

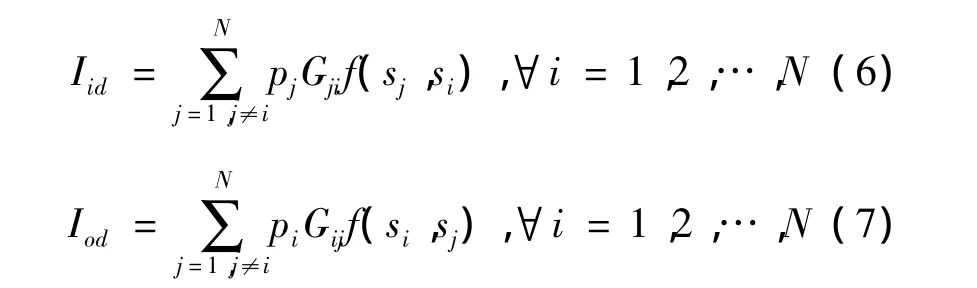
则效用函数ui的另一种表达方式为

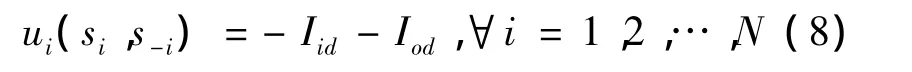
其中:Iid在接收端测量得到;Iod在发射端计算得出。虽然在采用ui的情况下，算法需要在公共信道上使用一个数据包来传递参与者对邻近节点干扰的测量信息，算法的复杂度会增加，但是效用函数的设计的确能满足最小化系统总干扰水平的目标要求。

位势博弈的特性是博弈中存在一个位势函数，该函数可以准确地反映任何参与者的效用函数中产生的单方面变化［7］。这个位势函数代替了具体的博弈效用函数反映效用的改善信息。一个确定的位势函数P定义为:

定义1 若存在一个函数，对所有的i和si，si'∈Si有这样的性质:

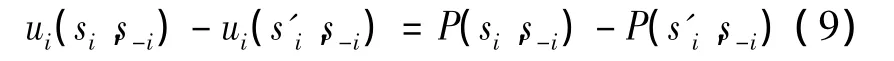
则称该函数为位势函数。

通过计算，对于效用函数ui的信道分配博弈，一个确定的位势函数为

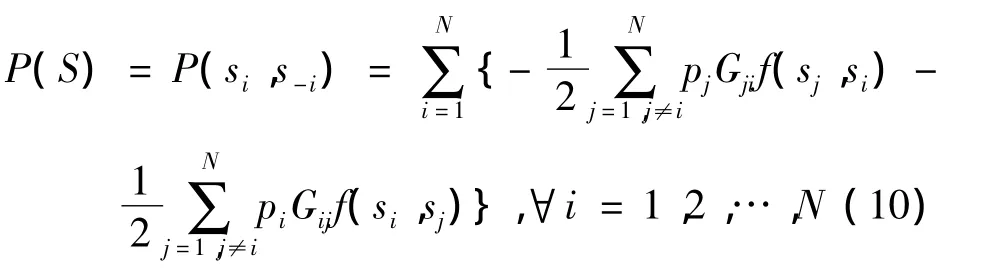
即

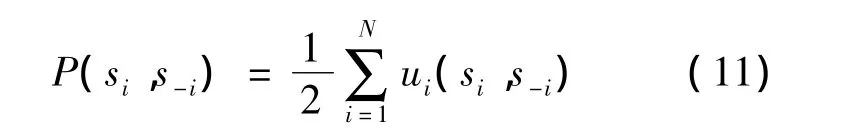
具体证明参照文献［8］。

3 算法实现以及算法改进

3.1 算法实现及过程

因为算法的实现需要接收端和发送端在一条公共信道上传输信令，因此设计一个3次握手机制的握手协议。

借鉴使用与IEEE802.11协议中的RTS-CTS交换协议相类似的协议，其中规定信令协议包如表1所示。

信令协议中的信令数据包主要起2个方面的作用:①测量各传输信道的干扰量，计算效用函数;②广播节点对于某条信道的使用情况。每个节点的接收端和发射端均保存一个信道状态表(CST)，用于记录各信道被其他节点占用的情况和储存数据流的目的节点和下一跳节点的信息。一旦用户侦听到公共信道中相应信道的信令数据包，则更新自身发送端和接收端的CST，以便掌握其他节点的信息。

表1 信令协议中数据包功能

算法的伪代码见算法1。

算法1资源分配算法

3.2 算法改进

虽然效用函数ui能实现系统的效用函数最大化，但是这种系统级的性能优化没有考虑到不同节点的业务需求，忽略了个性化的QoS需求和公平性。系统资源可能被少数节点占用，使其超过业务QoS需要的资源，而相当一部分节点占用的资源无法保证其业务最低的QoS要求。因此，需要对效用函数U进行必要的修正。

根据参考文献［7］的算法，引入功率调整方法，研究一种满足业务需求的分布式动态分配方案。每个节点根据自己的QoS需求和本地信息进行分布式信道选择和功率控制。本算法采用SINR来量化业务的QoS需求，既有:

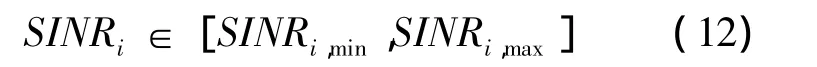
在式(4)的基础上对系统的目标进行扩展，可表示为

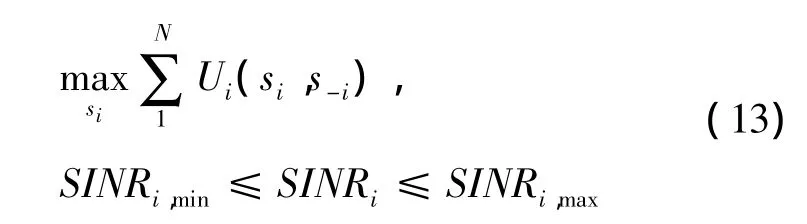
式(13)所示算法分为2个阶段来实现:第1阶段为信道分配，即每个用户通过博弈算法选择信道;第2阶段为功率调整，即在第1阶段结果的基础上，根据用户的QoS需求进行功率调整。

第2阶段的具体步骤:

根据第1阶段的分配结果，计算业务的信噪比SINR并调整功率，调整策略包括3种:

1)若 SINRi，min≤SINRi≤SINRi，max保持第 1 阶段的发射功率不变。

2)若 SINRi＜SINRi，min则用户需要增加自身发射功率，使得满足最小SINR要求，有2种情况:①若不存在使得，则关闭节点i的发送;②若存在，则

3)若 SINRi≥SINRi，max，则节点 i需要降低发射功率，使得满足最大SINR要求，既有SINRi，max，则然后将第2阶段的结果返回第1阶段进行迭代，直至收敛。

4 算法仿真

在仿真中评估了算法1和其改进算法的性能。网状节点随即分布在一个区域为200 mm的场景内。无线Mesh网络中的节点使用IEEE802.11b天线，设计一个接收接口和一个发送接口，在场景中随机分布20到50个节点，有一条信道作为公共信道用于传输信令数据包，可使用的正交信道数为2到8条，每个节点的发射功率不超过1 W。使用NS2.34作为仿真工具。

首先计算位势函数值(图2)，从中看出算法的收敛情况。当节点数为50，可用正交信道为4条重复计算80次得到2种算法的位势函数。由图2可以看出2种算法随着迭代次数的增加逐渐趋于收敛。算法1在迭代40次后进入收敛状态，而改进算法在迭代67次后才趋于收敛。由图2可知2种算法在前40次迭代中的位势函数值是相同的，但改进算法在达到算法1达到收敛之后还将继续判断各节点的SINR值是否满足用户需求，所以导致改进算法需要更多的迭代次数才能达到收敛。

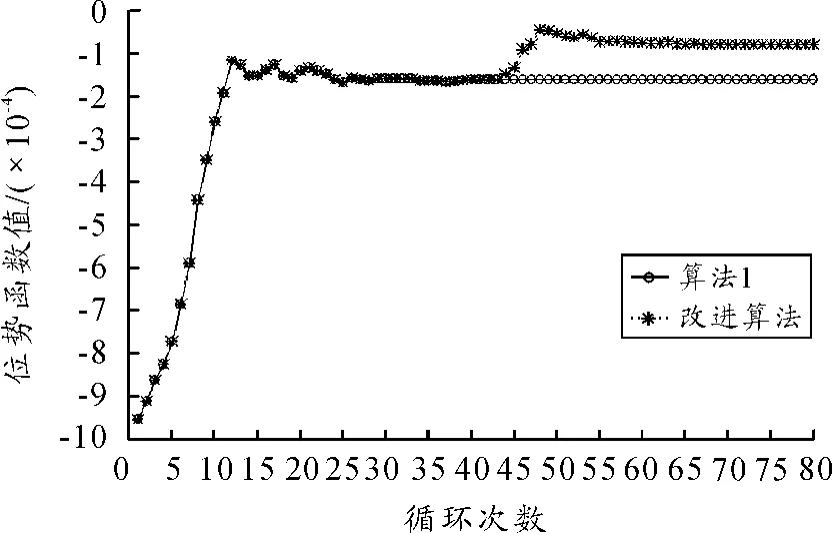
图2 2种算法位势函数收敛状况比较

从图3中可以看出:①在不同信道数量的情况下2种算法的收敛速度都是很快的，但是改进算法的收敛速度要慢于算法1。②当信道数量较少时，算法的收敛次数是增加的，这是因为在可用信道数较小的情况下网络中节点会频繁的切换信道;而当可用信道比较多时，2种算法的迭代至收敛的次数都会逐渐减小，这是因为在信道较多的情况下节点的信道选择会较快地达到稳定状态并保持在这一状态。

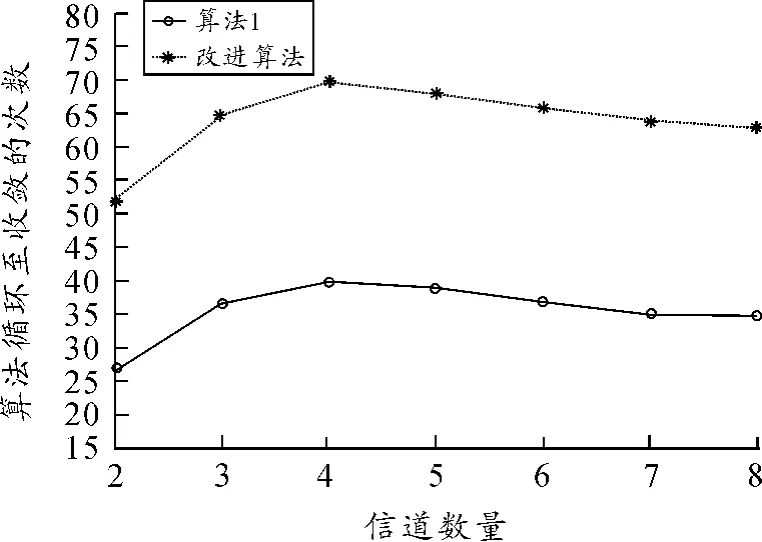
图3 2种算法的位势函数在不同信道数量下收敛状况的比较

图4和图5分别描述了2种算法的网络性能。图4为2种算法的系统吞吐量随着节点数量变换的结果，可以看出:系统吞吐量随着节点数量的增加而增加，且改进算法的系统吞吐量的变化幅度较大;在节点数比较少的情况下，算法1的系统吞吐量较大，但当节点数增多至30个以上是，改进算法的系统吞吐量变大，即节点数越多，改进算法的优势越明显。而从图5中可以看出，算法1的信道接入时延性能要优于改进算法，这是因为改进算法的复杂度要高于算法1。

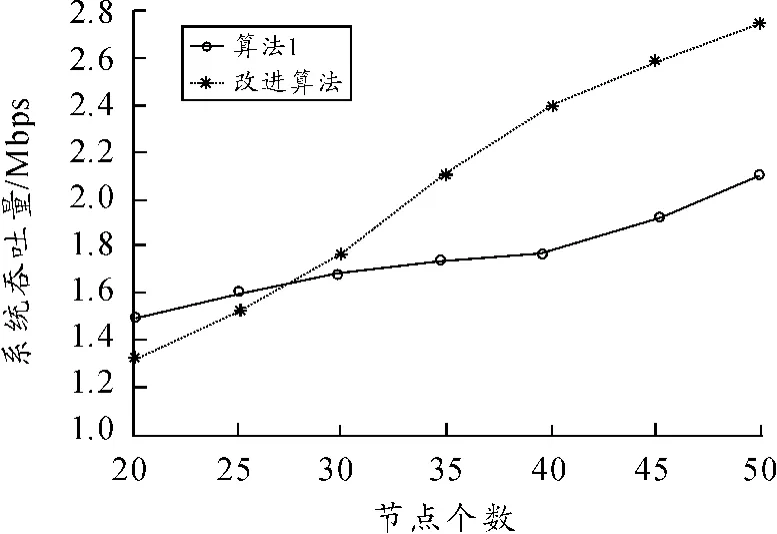
图4 2种算法的系统吞吐量随着节点数量变化的情况比较

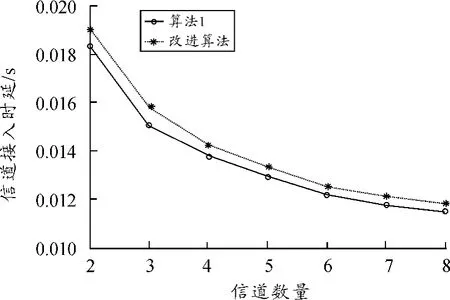
图5 2种算法的信道接入时延在不同信道数量下的变化

5 结束语

综上所述，利用博弈论设计无线Mesh网络的信道分配算法是一种行之有效的方法。本文采用博弈论的方法设计了一种效用函数来实现最大化网络信噪比的目的，并通过改变各节点发射功率的大小来提高个节点的QoS，使得网络资源能得到更为合理的利用。

［1］Akyildiz I，Wang X.A survey on wireless mesh networks［J］.IEEE Communications Magazine，2005，43(9)：23-30.

［2］Bruno R，Conti M，Gregori E.Mesh networks：commodity multi-hop ad hoc networks［J］.IEEE Communications Magazine，2005，43(3)：123-131.

［3］Audhya G K，Sinha K，Ghosh S C，et al.A survey on the channel assignment problem in wireless networks［J］.Wireless Communications and Mobile Computing，2011，11(5)：583-609.

［4］Kodialam M ，Nandagopai T.The effect of interference on the capacity of multi-hop wireless networks［M］.Chicago，IEEE Symposium on Information Theory，2004：470-479.

［5］Singh M，Saxena A.Secure computation for data privacy［C］//Proc SECCOM 07.Nice：［s.n.］，2007：58-62.

［6］Blough D，Resta G，Santi P.Approximation algorithms for wireless link scheduling with SINR-based interference［J］.IEEE/ACM Transactions on Networking(TON)，2010，18(6)：1701-1712.

［7］Mondere D，Shapley L.Potential Games and Economic［J］.Behavior，1996，14：124-143.

［8］Yu Q，Chen J，Fan Y，et al.Multi-channel assignment in wireless sensor networks：A game theoretic approach［C］//Proc of INFOCOM 10.San Diego：IEEE，2010：1-9.