基于UG的摆线齿锥齿轮的加工仿真

白 洋，张卫青，2，赵小波

(1.重庆理工大学 重庆汽车学院，重庆 400054;2.重庆市科学技术研究院，重庆 401123)

螺旋锥齿轮是传递相交轴及相错轴间运动和动力的重要传动零件。该类齿轮按齿线类型可分为弧线齿和摆线齿2种齿制。近年来，由于摆线齿锥齿轮具有承载能力高、传动平稳与结构紧凑等特点，已经在汽车后桥上得到较为广泛的使用。但由于相关资料文献较少，国内对摆线齿锥齿轮的研究还处于起步阶段，在实际加工中仍存在着很多问题。因此，有必要在实际切齿加工前验证切齿方法的正确性。本文通过分析切齿加工过程中刀盘、摇台与齿轮间的相对位置与运动关系，建立了摆线齿锥齿轮的数学模型，并通过UG软件进行加工仿真，获得了摆线齿锥齿轮的三维模型，对提高摆线齿锥齿轮的开发效率、了解齿形结构特点、降低加工成本具有一定的指导意义。

1 摆线齿锥齿轮切齿加工原理

摆线齿锥齿轮通常采用连续分齿的方法进行加工。这种加工方法的原理是利用同一假想的产形轮展成相配的两齿面，从而形成具有完全共轭特性的一对齿轮副，再采用曲率修正方法来实现具有局部接触特性的齿面。如图1所示，刀盘在绕自身轴线旋转的同时，也绕着摇台轴线进行公转，可视为刀盘上一滚圆与摇台上的一基圆做纯滚动，这时刀齿上一点所形成的运动轨迹就是延伸外摆线。加工过程中，刀盘每转过一组刀齿，产形轮就转过一个齿，产形轮与齿坯按定比关系做展成运动，所形成的轨迹就是摆线齿锥齿轮的齿面。本文以奥利康制刀倾半展成法为例，对摆线齿锥齿轮的加工方法进行了说明，即大轮采用成形法加工，小轮采用展成法加工［1-5］。

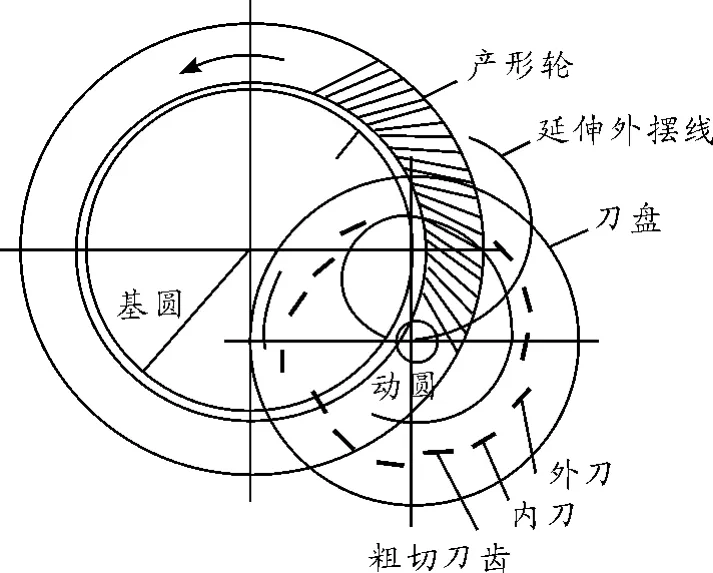
图1 摆线齿加工原理

2 切齿加工仿真运动控制方法

切齿加工过程中，齿坯、刀具与机床的相对位置决定着所加工齿轮的特征。刀倾半展成法的原理是大轮采用成形法加工，小轮采用一个与大轮相似的产形轮来展成加工。由此可知，齿轮的齿面是由产形面做展成运动形成的。所以，在进行仿真时，首先需要建立产形面方程并构建产形轮模型。图2为切齿加工时产形轮与齿坯的相对位置关系［6-8］。

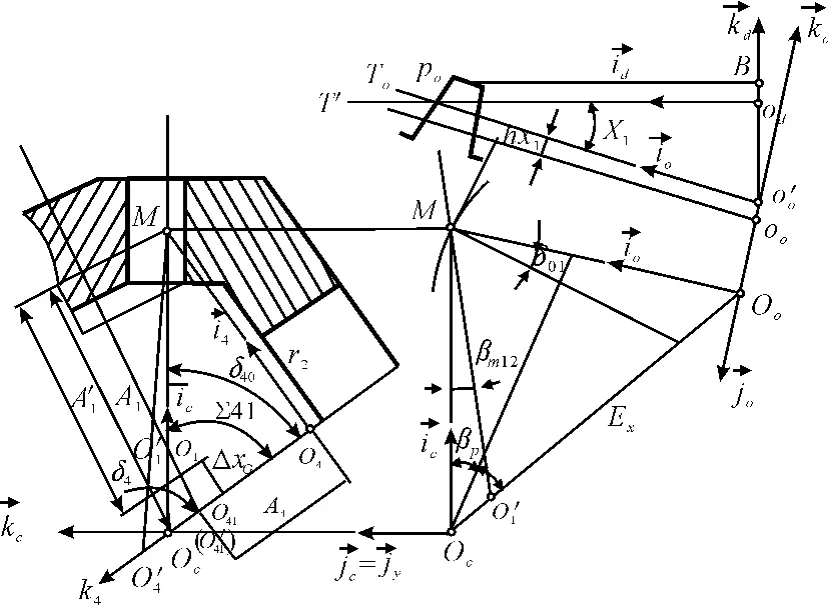
图2 产形轮与齿坯相对位置

2.1 产形轮建模实现

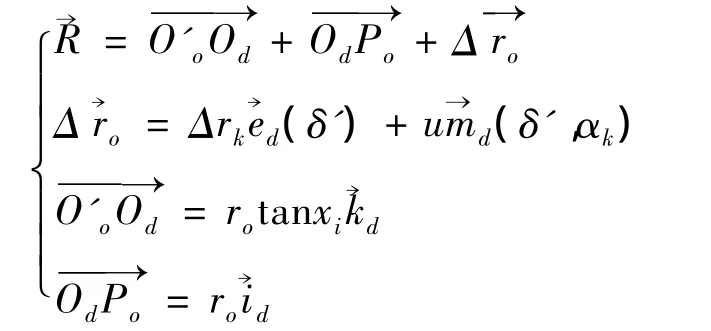
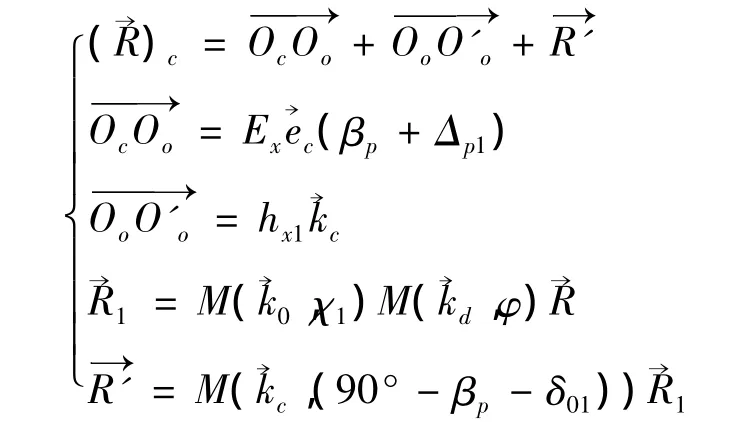
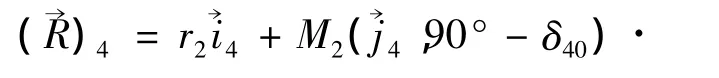
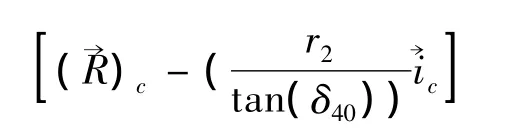
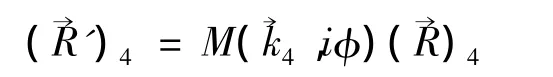
式中:u为刀齿上任一点到刀齿节点的距离;Δrk为切齿内外刀半径修正量;δ'为刀齿方向角;αk为内外刀刀具齿形角;其余参数如图2所示［2-3］。矩阵为球面矢量旋转矩阵［1］。修正参数使产形轮满足要求后，可以得到Q点在σ4下的一系列径矢坐标，即产形面方程。通过三维软件中样条曲线的功能将这些点连接成曲线，利用网格曲面构建产形轮的齿面，并缝合生成实体模型。

2.2 加工仿真中的运动控制

齿轮加工的过程是在齿坯上去除材料的过程，即由产形轮展成齿轮的过程，在三维软件中可以通过布尔运算来实现。成型法加工大轮时并没有产形轮，整个刀刃在齿坯上的相对运动轨迹就是大轮齿面。

与成型法不同，小轮齿面是产形轮齿面与小轮通过展成运动产生的，每个时刻齿坯与产形轮轮齿的相对位置都会发生变化。首先以O'1为原点构建齿坯模型，按照切齿加工时的水平轮位ΔXG、床位XBG、安装根锥角 Γ、垂直轮位 Emr和展成时产形轮与夹角φt的大小，并由图2所示几何关系推导出公式(1)，最终确定产形轮轮齿与小轮齿坯间的相对位置。式(1)中:ε为产形轮偏离角;rp为大轮参考点分度圆半径。

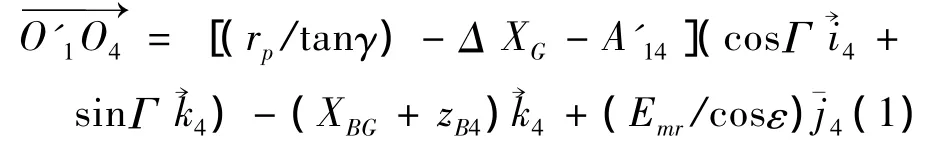
在计算得到点O4的位置后，在UG中建立坐标系在坐标系σ4下构建产形轮模型，并以展成起始角度φs放置产形轮的一个轮齿，这时齿坯与已经建立好的产形轮轮齿实体模型出现重叠的区域，通过布尔运算去除齿坯上的材料，得到小轮齿面的部分区域。令工具体绕轴旋转一定的步距角增量dφ，则任意时刻工具体与轴的夹角为

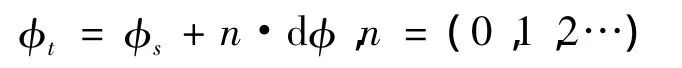
根据切齿加工的滚比，同时令齿坯绕其轴线旋转i·n·φt。当不断改变n时，便会出现新的瞬时重叠区域，通过布尔运算将其去除，直到工具体与齿坯间不再有重叠区域时，便得到了小轮上一个完整的齿槽［5］。小轮切齿加工模型如图3所示。

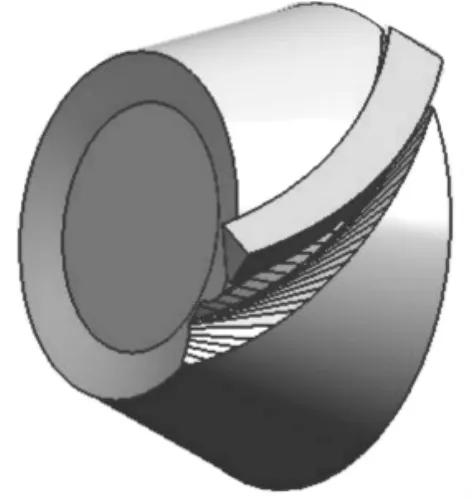
图3 小轮切齿加工模型

3 加工仿真实例

本文以10X41的一对齿轮副为例进行仿真。表1为齿轮副的基本几何参数，表2为切齿加工机床调整参数与刀盘参数。

表1 摆线齿锥齿轮基本几何参数

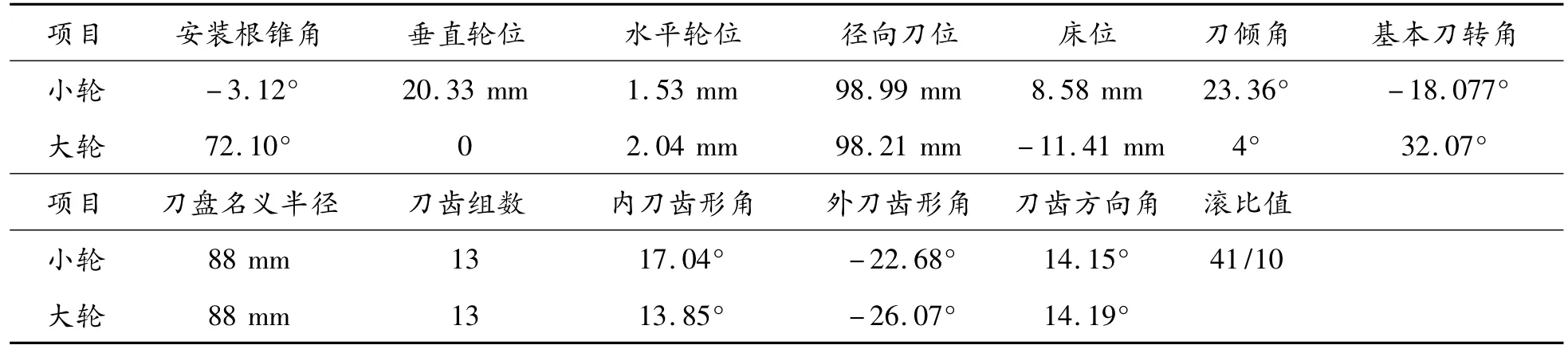
表2 切齿加工机床调整参数与刀盘参数

根据表1列出的参数在UG中建立产形轮和齿坯模型，通过加工仿真中的运动控制方法来调整产形轮和齿坯的相对位置，利用布尔运算逐步进行切齿，最后获得齿轮模型。图4为切齿加工后的大轮模型，图5为切齿加工后的小轮模型，图6为以齿面方程直接构建的理论小轮模型。

图4 切齿加工后的大轮模型

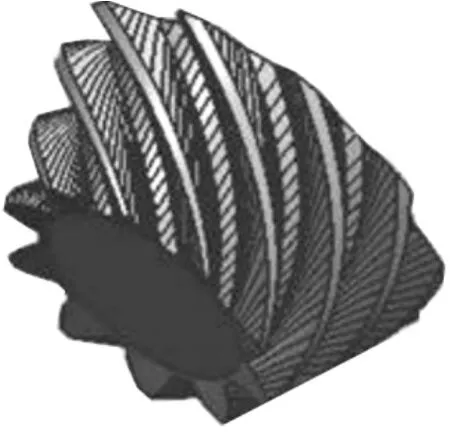
图5 切齿加工后的小轮模型

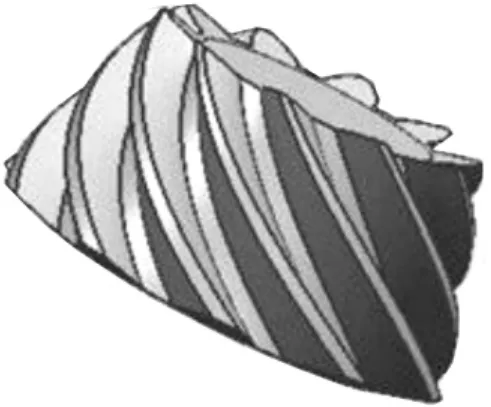
图6 理论小轮模型

为了验证仿真切齿加工后的齿轮齿面的正确性，提取加工后齿面上的网格点，与通过齿面方程所计算出的理论齿面进行比较。图7为提取的点云与真实齿面在Imageware中的误差分析云图。从误差结果上看，最大误差为4.22 μm，该误差是由于切齿加工过程中步距角取值所产生。当步距角越小时，切齿仿真精度越高，与理论齿面之间的误差也就越小。

将在UG中获得的大、小轮模型按照安装位置装配，进行运动仿真(如图8所示)，可以看到二者之间有较好的接触区，不会产生多余的干涉。

图7 实际齿面与理论齿面误差分析云图

图8 运动仿真

4 结束语

本文根据摆线齿锥齿轮加工的基本原理，建立了产形轮数学模型与切齿加工运动控制模型，并根据以上原理在三维软件UG中实现了摆线齿锥齿轮切齿加工仿真。通过将加工仿真得到的齿面模型与理论齿面进行比较，验证了加工仿真过程的正确性。运用本文的方法，可以减少实际加工的试切次数，有效避免齿顶变尖、根切与运动干涉的现象，从而提高加工效率、降低加工成本，同时也可以为摆线齿锥齿轮的齿面接触分析和有限元分析提供三维实体模型。

［1］董学朱.摆线齿锥齿轮及准双曲面齿轮设计和制造［M］.北京：机械工业出版社，2002.

［2］李巍，李剑锋，王青云.克林贝格摆线齿锥齿轮齿面方程及图形仿真［J］.机械科学与技术，2006，25(12)：1462-1466.

［3］邹旻，丁军.摆线齿锥齿轮的产成原理及其产形面方程［J］.机械传动，2011，35(6)：31-33.

［4］吴银联，魏洪钦，王晓椿.延伸外摆线锥齿轮的成型原理及齿面结构研究［J］.西安交通大学学报，2001，35(1)：43-46.

［5］张卫青，郭晓东，张明德.摆线齿锥齿轮铣齿机的运动及加工仿真研究［J］.制造技术与机床，2011，9：109-112.

［6］Qi Fan.Computerized Modeling and Simulation of Spiral Bevel and Hypoid Gears Manufactured by Gleason Face Hobbing Process［J］.Journal of Mechanical Design，2006，128：235-241.

［7］Vimercati M.Mathematical model for tooth surface representation of face-hobbed hypoid gears and its application to contact analysis and stress calculation［J］.Mechanism and Machine Theory，2007(42)：668-690.

［8］董学朱.摆线齿锥齿轮连续分齿法铣齿原理的研究［J］.机械传动，1999，23：29-3.